华师大版数学七年级上册第一章第一节1.1数学伴我们成长同步练习
文档属性
| 名称 | 华师大版数学七年级上册第一章第一节1.1数学伴我们成长同步练习 |  | |
| 格式 | doc | ||
| 文件大小 | 179.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-21 09:46:52 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
华师大版数学七年级上册第一章第一节1.1数学伴我们成长同步练习
一、选择题
1.一个数加7,再乘以3,然后减去12,再除以6,最后得到8,则这个数是( )
A.12 B.13 C.14 D.15
答案:B
解答:可以利用倒推法进行解题,这个数为.
分析:运算中,加法与减法是互逆运算,乘法与除法是互逆运算.
2.联欢会上,小明按4个红气球,3个黄气球,2个绿气球的顺序把气球串起来装饰会场,则第100个气球的颜色是( )
A.绿色 B.黄色 C.红色 D.不确定
答案:C
解答:根据题意可知气球排列的一个循环节为4+3+2=9,而的余数为1,所以第100个气球的颜色与第1个气球的颜色相同,都为红色.
分析:探索图形规律的关键在于找准循环节.
3.如果a,b是任意两个不等于零的数,定义运算如下(其余符号意义如常):,那么的值是( )
A. B.5 C.6 D.
答案:A
解答:原式.
分析:在进行本题目的计算时要逐步计算,以免粗心算错.
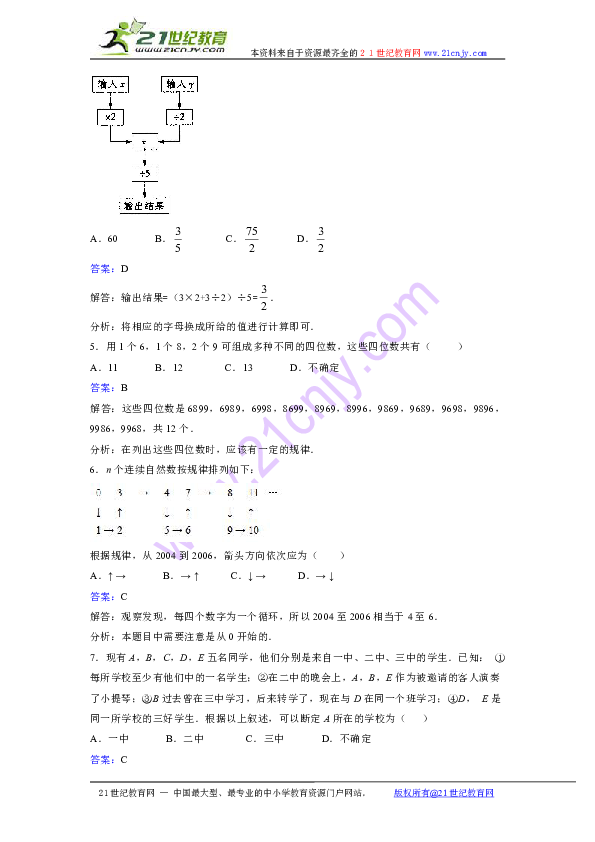
4.下图是一个数值转换机的示意图,若输入的x的值是3,y的值是3,则输出的结果为( )
A.60 B. C. D.
答案:D
解答:输出结果=(3×2+3÷2)÷5=.
分析:将相应的字母换成所给的值进行计算即可.
5.用1个6,1个8,2个9可组成多种不同的四位数,这些四位数共有( )
A.11 B.12 C.13 D.不确定
答案:B
解答:这些四位数是6899,6989,6998,8699,8969,8996,9869,9689,9698,9896,9986,9968,共12个.
分析:在列出这些四位数时,应该有一定的规律.
6.n个连续自然数按规律排列如下:
根据规律,从2004到2006,箭头方向依次应为( )
A.↑ → B.→ ↑ C.↓ → D.→ ↓
答案:C
解答:观察发现,每四个数字为一个循环,所以2004至2006相当于4至6.
分析:本题目中需要注意是从0开始的.
7.现有A,B,C,D,E五名同学,他们分别是来自一中、二中、三中的学生.已知:①每所学校至少有他们中的一名学生;②在二中的晚会上,A,B,E作为被邀请的客人演奏了小提琴;③B过去曾在三中学习,后来转学了,现在与D在同一个班学习;④D,E是同一所学校的三好学生.根据以上叙述,可以断定A所在的学校为( )
A.一中 B.二中 C.三中 D.不确定
答案:C
解答:由②、③可知B不在二中和三中,所以B在一中,结合④可以判断D,E也在一中,而每所学校至少有他们五人中的一人,由②可知A不在二中,所以在三中,因此C在二中.
分析:根据每一句话作出一定判断后,要记得题目的大前提是:每所学校至少有他们中的一名学生.
8.在A,B,C三个盒子中分别装有红、黄、蓝颜色的小球中的一种,将它们分别给甲、乙、丙三个人.已知甲没有得到A盒;乙没有得到B盒,也没有得到黄球;A盒中没有装红球,B盒中装着蓝球.则丙得到的盒子编号小球的颜色分别是( )
A.A 黄色 B.B 蓝色 C.C 红色 D.无法确定
答案:A
解答:因为“A盒中没有装红球,B盒中装着蓝球”,所以可以判定:A盒中装的是黄球,C盒中装着红球;因为“乙没有得到B盒,也没有得到黄球”,所以可以判定:乙得到C盒;再根据“甲没有得到A盒”,可以判定:甲得到B盒,丙得到A盒中的黄球.
分析:本类题目的关键在于找到可以作出初次判断的语句.
9.找出一列数2,3,5,8,13,□,34的规律,在□里填上( )
A.20 B.21 C.22 D.24
答案:B
解答:5=2+3,8=3+5,13=5+8,□=8+13=21,34=13+21.
分析:这一组的数字规律是从第三个数字起,后一个数字是前两个数字的和.
10.如图,是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C内填入适当的数,使它们折成正方体后相对的面上的两个数互为倒数,则填入正方形A,B,C的三个数依次为( )
A.,,1 B.,1, C.1,, D.1,,
答案:C
解答:折成正方体后,A与1相对,B与2相对,C与3相对,且相对的两个数互为倒数,所以正方形A,B,C的三个数依次为1,,.
分析:可以按照所给的展开图作一个模型,动手进行折叠.
11.某学生在暑假期间观察了x天的天气情况,其结果是:①共有7天上午是晴天;②共有5天下午是晴天;③共下了8次雨;④下午下雨的那天,上午是晴天.则x的值为( )
A.8 B.9 C.10 D.11
答案:C
解答:由题意知,他们每天上午、下午各测一次,七次上午晴,五次下午晴,共下八次雨,所以共测了20次,所以是10天.
分析:本问题的关键在于“他们每天上午、下午各测一次”.
12.把14个棱长为1的正方体在地面上堆叠如图所示的立体,然后将露出的表面部分涂成红色,那么红色部分的面积为( )
A.21 B.24 C.33 D.37
答案:C
解答:相当于涂了底层的正面和每层的侧面,则共有9+4+8+12=33.
分析:本题对于“相当于涂了底层的正面”的理解为:最上层涂的表面积为1,中层涂的表面积为4-1=3,底层涂的表面积为9-4=5.
13.春节晚会上,电工师傅在礼堂四周挂了一圈只有绿、黄、蓝、红四种颜色的彩灯,其排列规律是:绿黄黄红蓝红红绿黄黄红蓝红红绿黄黄红蓝红红绿黄黄红蓝红红……那么,第2006个彩电的颜色是( )
A.绿色 B.黄色 C.红色 D.蓝色
答案:C
解答:观察发现,每七个为一个循环,而2006除以7的余数为4,而第四个是红色,所以第2006个彩电的颜色是红色.
分析:此类题目的关键在于找到循环的规律.
14.根据图中骰子的三种不同状态显示的数字,推出?处的数字是( )
A.1 B.2 C.3 D.6
答案:D
解答:由图发现,1和2,3,4,5都相邻,所以1对的数字应是6.
分析:可以作一个正方体的模型进行操作.
15.给出两列数:1,3,5,7,9,…,2001和6,11,16,…,2001,同时出现在这两列数中的数的个数为( )
A.199 B.200 C.201 D.202
答案:B
解答:同时出现在两个数列中的数为11,21,31,41,…,1991,2001,共200个.
分析:第一列数为1与2001之间的奇数,第二列为前一个数加5得到,所以同时出现在这两列数中的数的个数为第二列中的所有奇数即:从11起,后一个数由前一个数加10得到.
二、填空题
16.某课外活动小组测得自己学校的篮球场长A(m),宽B(m),它的长比宽多C(m),周长是D(m),面积是E(),篮球架高F(m).提供信息:(86,13,420,15,28,3),由于记录疏忽,数据被弄乱了,你能帮他们整理一下吗?
A=_______,B=________,C=________,D=_______,E=________,F=________.
答案:28|15|13|86|420|3
解答:根据已有知识我们可以知道:最大数据420最有可能是面积,而两个数积的个位数为0的只可能是个位数为5与8的数字,且28与15的积为420,所以A代表的数字为28,B代表的数字为15,所以C代表的数字为13,D代表的数字为86,因此F代表的数字只能为3.
分析:面积是两个数的积,所以最大的数据优先考虑为面积,这是本题目的突破口.
17.用尺量一下,下面两个图形面积的大小关系是_________.
甲 乙
答案:
解答:如下图,原图形的面积分别等于两个边个相等的正方形的面积.
甲 乙
分析:割补法是求不规则平面图形面积中常常用到的一种方法.
18.对A,B,C有如下的计算规定:2→A→4,5→A→7,7→B→4,10→B→7,1→C→4,3→C→12.请在横线上填上适当的数或相应的字母:
(1)14→B→A→C→________;
答案:52
(2)5→C→B→_______.
答案:17
解答:根据题意可知,A代表的运算为加2,B代表的运算为减3,C代表的运算为乘4,从而可以计算出14→B→A→C→52;5→C→B→17.
分析:本题目的关键在于确定A、B、C分别代表的运算.
19.把一根绳子对折后再对折,然后在其一个三等分处剪断,这样变成了______根绳子,其中最长的是最短的长度的_________倍.
答案:5|4或2
解答:5根,当靠近绳头的三等分处剪断时,最长的是,最短的,则答案是4倍;
当远离绳头的三等分处剪断,最长的是,最短的,则答案是2倍.
分析:可以动手进行操作.
20.观察下列算式:
…利用你所发现的规律,写出的末位数(个位上的数字):________.
答案:4
解答:末位数以2,4,8,6的顺序周而复始,而30=4×7+2.
分析:关键在于找寻末位数字的规律.
三、解答题
21.如图,A,B,C,D,E五人围坐在圆桌旁,为A祝贺生日,小华问他们当时的座位.
A说:“我在B的旁边.”
B说:“我在左边不是C就是D.”
C说:“我在D的旁边.”
D说:“不,C在B的右边是错的.”
只有E作了如实回答:“除B说正确之外,A,C,D都说错了.”你能确定他们的位置吗?
答案:解:如下图所示,有两种可能性.
分析:B的位置是本题的关键位置.
22.如图所示,有25个点,横竖都以相等的间隔排列,请你想出尽可能多的方法,将点连成面积不同的正方形.图中一共给出8个备用栏,但不一定有8个答案,请在一个备用栏里画出一个图形.
答案:
解答:解:如下图所示,有7种可能性.
分析:注意面积共有七种可能,但是所连点可以不同.
23.房间里有3盏灯,全部关着.现在每次拉两盏灯的开关,这样做几次后,问有没有可能使3盏灯全部是亮的?
答案:不可能
解答:解:直接用试探的方法去做.为此需要用简单明白的符号表示开着的灯和关着的灯.
如下图,我们采用有阴影及空白圆圈表示关着及开着的灯.
一开始3盏灯全关着(如下图的(1)),然后随便打开两盏灯,比如打开第一、二两盏灯(如下图的(2)).
(1)三盏灯全关着 (2)打开两盏灯
下面要再拉两盏灯的开关.如果拉第一、二盏灯的开关,则3盏灯全变成关着的,我们不希望倒退到开始的情况,因而只能拉第一、三盏灯或拉第二、三盏灯的开关,这样仍得到图(2)所表示的结果:两盏灯开着,一盏灯关着.
做到这里我们已经可以肯定,这样下去无论拉多少次,都不可能使3盏灯全开着.
分析:在这个例子里,由于灯的总数很少,所以采用尝试法用不了几步就可以得到正确的结果.但如果灯有许多盏,用这样的方法做,由于不同可能的拉线方法太多,很容易被弄糊涂.此外,这种方法没能告诉我们“不可能”的原因在什么地方,故需要寻找新的方法.
24.小明从1写到100,他共写了多少个数字“1”?
答案:21
解答:解:“1”出现在个位数上的数有:1、11、21、31、41、51、61、71、81、91共10个;“1”出现在十位数上的数有:10、11、12、13、14、15、16、17、18、19共10个;“1”出现在百位数上的数有:100共1个;所以共计:10+10+1=21.
分析:分类思想是数学中最常用的一个数学思想.
25.将连续的自然数1至1001按下图的方式排成一个长方形阵列,用一个长方形框出16个数,要使这个长方形框出的16个数之和分别等于(1)1998,(2)1991,(3)2000,(4)2080,这是否可能?若不可能,试说明理由.
答案:不可能|(2)不可能|(3)可能|(4)可能
解答:解:设第一个数为x,则第一行为x,x+1,x+2,x+3,第二行为x+7,x+8,x+9,x+10,第三行为x+14,x+15,x+16,x+17,第四行为x+21,x+22,x+23,x+24,所以16个数之和为16x+192.
(1)16x+192=1988,x=112,所以不可能;
(2)16x+192=1991,x=112,所以不可能;
(3)16x+192=2000,x=113,所以可能,最小数为113,最大数为137;
(4)16x+192=2080,x=118,所以可能,最小数为118,最大数为142.
分析:方程的思想是数学的另一个重要思想.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
华师大版数学七年级上册第一章第一节1.1数学伴我们成长同步练习
一、选择题
1.一个数加7,再乘以3,然后减去12,再除以6,最后得到8,则这个数是( )
A.12 B.13 C.14 D.15
答案:B
解答:可以利用倒推法进行解题,这个数为.
分析:运算中,加法与减法是互逆运算,乘法与除法是互逆运算.
2.联欢会上,小明按4个红气球,3个黄气球,2个绿气球的顺序把气球串起来装饰会场,则第100个气球的颜色是( )
A.绿色 B.黄色 C.红色 D.不确定
答案:C
解答:根据题意可知气球排列的一个循环节为4+3+2=9,而的余数为1,所以第100个气球的颜色与第1个气球的颜色相同,都为红色.
分析:探索图形规律的关键在于找准循环节.
3.如果a,b是任意两个不等于零的数,定义运算如下(其余符号意义如常):,那么的值是( )
A. B.5 C.6 D.
答案:A
解答:原式.
分析:在进行本题目的计算时要逐步计算,以免粗心算错.
4.下图是一个数值转换机的示意图,若输入的x的值是3,y的值是3,则输出的结果为( )
A.60 B. C. D.
答案:D
解答:输出结果=(3×2+3÷2)÷5=.
分析:将相应的字母换成所给的值进行计算即可.
5.用1个6,1个8,2个9可组成多种不同的四位数,这些四位数共有( )
A.11 B.12 C.13 D.不确定
答案:B
解答:这些四位数是6899,6989,6998,8699,8969,8996,9869,9689,9698,9896,9986,9968,共12个.
分析:在列出这些四位数时,应该有一定的规律.
6.n个连续自然数按规律排列如下:
根据规律,从2004到2006,箭头方向依次应为( )
A.↑ → B.→ ↑ C.↓ → D.→ ↓
答案:C
解答:观察发现,每四个数字为一个循环,所以2004至2006相当于4至6.
分析:本题目中需要注意是从0开始的.
7.现有A,B,C,D,E五名同学,他们分别是来自一中、二中、三中的学生.已知:①每所学校至少有他们中的一名学生;②在二中的晚会上,A,B,E作为被邀请的客人演奏了小提琴;③B过去曾在三中学习,后来转学了,现在与D在同一个班学习;④D,E是同一所学校的三好学生.根据以上叙述,可以断定A所在的学校为( )
A.一中 B.二中 C.三中 D.不确定
答案:C
解答:由②、③可知B不在二中和三中,所以B在一中,结合④可以判断D,E也在一中,而每所学校至少有他们五人中的一人,由②可知A不在二中,所以在三中,因此C在二中.
分析:根据每一句话作出一定判断后,要记得题目的大前提是:每所学校至少有他们中的一名学生.
8.在A,B,C三个盒子中分别装有红、黄、蓝颜色的小球中的一种,将它们分别给甲、乙、丙三个人.已知甲没有得到A盒;乙没有得到B盒,也没有得到黄球;A盒中没有装红球,B盒中装着蓝球.则丙得到的盒子编号小球的颜色分别是( )
A.A 黄色 B.B 蓝色 C.C 红色 D.无法确定
答案:A
解答:因为“A盒中没有装红球,B盒中装着蓝球”,所以可以判定:A盒中装的是黄球,C盒中装着红球;因为“乙没有得到B盒,也没有得到黄球”,所以可以判定:乙得到C盒;再根据“甲没有得到A盒”,可以判定:甲得到B盒,丙得到A盒中的黄球.
分析:本类题目的关键在于找到可以作出初次判断的语句.
9.找出一列数2,3,5,8,13,□,34的规律,在□里填上( )
A.20 B.21 C.22 D.24
答案:B
解答:5=2+3,8=3+5,13=5+8,□=8+13=21,34=13+21.
分析:这一组的数字规律是从第三个数字起,后一个数字是前两个数字的和.
10.如图,是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C内填入适当的数,使它们折成正方体后相对的面上的两个数互为倒数,则填入正方形A,B,C的三个数依次为( )
A.,,1 B.,1, C.1,, D.1,,
答案:C
解答:折成正方体后,A与1相对,B与2相对,C与3相对,且相对的两个数互为倒数,所以正方形A,B,C的三个数依次为1,,.
分析:可以按照所给的展开图作一个模型,动手进行折叠.
11.某学生在暑假期间观察了x天的天气情况,其结果是:①共有7天上午是晴天;②共有5天下午是晴天;③共下了8次雨;④下午下雨的那天,上午是晴天.则x的值为( )
A.8 B.9 C.10 D.11
答案:C
解答:由题意知,他们每天上午、下午各测一次,七次上午晴,五次下午晴,共下八次雨,所以共测了20次,所以是10天.
分析:本问题的关键在于“他们每天上午、下午各测一次”.
12.把14个棱长为1的正方体在地面上堆叠如图所示的立体,然后将露出的表面部分涂成红色,那么红色部分的面积为( )
A.21 B.24 C.33 D.37
答案:C
解答:相当于涂了底层的正面和每层的侧面,则共有9+4+8+12=33.
分析:本题对于“相当于涂了底层的正面”的理解为:最上层涂的表面积为1,中层涂的表面积为4-1=3,底层涂的表面积为9-4=5.
13.春节晚会上,电工师傅在礼堂四周挂了一圈只有绿、黄、蓝、红四种颜色的彩灯,其排列规律是:绿黄黄红蓝红红绿黄黄红蓝红红绿黄黄红蓝红红绿黄黄红蓝红红……那么,第2006个彩电的颜色是( )
A.绿色 B.黄色 C.红色 D.蓝色
答案:C
解答:观察发现,每七个为一个循环,而2006除以7的余数为4,而第四个是红色,所以第2006个彩电的颜色是红色.
分析:此类题目的关键在于找到循环的规律.
14.根据图中骰子的三种不同状态显示的数字,推出?处的数字是( )
A.1 B.2 C.3 D.6
答案:D
解答:由图发现,1和2,3,4,5都相邻,所以1对的数字应是6.
分析:可以作一个正方体的模型进行操作.
15.给出两列数:1,3,5,7,9,…,2001和6,11,16,…,2001,同时出现在这两列数中的数的个数为( )
A.199 B.200 C.201 D.202
答案:B
解答:同时出现在两个数列中的数为11,21,31,41,…,1991,2001,共200个.
分析:第一列数为1与2001之间的奇数,第二列为前一个数加5得到,所以同时出现在这两列数中的数的个数为第二列中的所有奇数即:从11起,后一个数由前一个数加10得到.
二、填空题
16.某课外活动小组测得自己学校的篮球场长A(m),宽B(m),它的长比宽多C(m),周长是D(m),面积是E(),篮球架高F(m).提供信息:(86,13,420,15,28,3),由于记录疏忽,数据被弄乱了,你能帮他们整理一下吗?
A=_______,B=________,C=________,D=_______,E=________,F=________.
答案:28|15|13|86|420|3
解答:根据已有知识我们可以知道:最大数据420最有可能是面积,而两个数积的个位数为0的只可能是个位数为5与8的数字,且28与15的积为420,所以A代表的数字为28,B代表的数字为15,所以C代表的数字为13,D代表的数字为86,因此F代表的数字只能为3.
分析:面积是两个数的积,所以最大的数据优先考虑为面积,这是本题目的突破口.
17.用尺量一下,下面两个图形面积的大小关系是_________.
甲 乙
答案:
解答:如下图,原图形的面积分别等于两个边个相等的正方形的面积.
甲 乙
分析:割补法是求不规则平面图形面积中常常用到的一种方法.
18.对A,B,C有如下的计算规定:2→A→4,5→A→7,7→B→4,10→B→7,1→C→4,3→C→12.请在横线上填上适当的数或相应的字母:
(1)14→B→A→C→________;
答案:52
(2)5→C→B→_______.
答案:17
解答:根据题意可知,A代表的运算为加2,B代表的运算为减3,C代表的运算为乘4,从而可以计算出14→B→A→C→52;5→C→B→17.
分析:本题目的关键在于确定A、B、C分别代表的运算.
19.把一根绳子对折后再对折,然后在其一个三等分处剪断,这样变成了______根绳子,其中最长的是最短的长度的_________倍.
答案:5|4或2
解答:5根,当靠近绳头的三等分处剪断时,最长的是,最短的,则答案是4倍;
当远离绳头的三等分处剪断,最长的是,最短的,则答案是2倍.
分析:可以动手进行操作.
20.观察下列算式:
…利用你所发现的规律,写出的末位数(个位上的数字):________.
答案:4
解答:末位数以2,4,8,6的顺序周而复始,而30=4×7+2.
分析:关键在于找寻末位数字的规律.
三、解答题
21.如图,A,B,C,D,E五人围坐在圆桌旁,为A祝贺生日,小华问他们当时的座位.
A说:“我在B的旁边.”
B说:“我在左边不是C就是D.”
C说:“我在D的旁边.”
D说:“不,C在B的右边是错的.”
只有E作了如实回答:“除B说正确之外,A,C,D都说错了.”你能确定他们的位置吗?
答案:解:如下图所示,有两种可能性.
分析:B的位置是本题的关键位置.
22.如图所示,有25个点,横竖都以相等的间隔排列,请你想出尽可能多的方法,将点连成面积不同的正方形.图中一共给出8个备用栏,但不一定有8个答案,请在一个备用栏里画出一个图形.
答案:
解答:解:如下图所示,有7种可能性.
分析:注意面积共有七种可能,但是所连点可以不同.
23.房间里有3盏灯,全部关着.现在每次拉两盏灯的开关,这样做几次后,问有没有可能使3盏灯全部是亮的?
答案:不可能
解答:解:直接用试探的方法去做.为此需要用简单明白的符号表示开着的灯和关着的灯.
如下图,我们采用有阴影及空白圆圈表示关着及开着的灯.
一开始3盏灯全关着(如下图的(1)),然后随便打开两盏灯,比如打开第一、二两盏灯(如下图的(2)).
(1)三盏灯全关着 (2)打开两盏灯
下面要再拉两盏灯的开关.如果拉第一、二盏灯的开关,则3盏灯全变成关着的,我们不希望倒退到开始的情况,因而只能拉第一、三盏灯或拉第二、三盏灯的开关,这样仍得到图(2)所表示的结果:两盏灯开着,一盏灯关着.
做到这里我们已经可以肯定,这样下去无论拉多少次,都不可能使3盏灯全开着.
分析:在这个例子里,由于灯的总数很少,所以采用尝试法用不了几步就可以得到正确的结果.但如果灯有许多盏,用这样的方法做,由于不同可能的拉线方法太多,很容易被弄糊涂.此外,这种方法没能告诉我们“不可能”的原因在什么地方,故需要寻找新的方法.
24.小明从1写到100,他共写了多少个数字“1”?
答案:21
解答:解:“1”出现在个位数上的数有:1、11、21、31、41、51、61、71、81、91共10个;“1”出现在十位数上的数有:10、11、12、13、14、15、16、17、18、19共10个;“1”出现在百位数上的数有:100共1个;所以共计:10+10+1=21.
分析:分类思想是数学中最常用的一个数学思想.
25.将连续的自然数1至1001按下图的方式排成一个长方形阵列,用一个长方形框出16个数,要使这个长方形框出的16个数之和分别等于(1)1998,(2)1991,(3)2000,(4)2080,这是否可能?若不可能,试说明理由.
答案:不可能|(2)不可能|(3)可能|(4)可能
解答:解:设第一个数为x,则第一行为x,x+1,x+2,x+3,第二行为x+7,x+8,x+9,x+10,第三行为x+14,x+15,x+16,x+17,第四行为x+21,x+22,x+23,x+24,所以16个数之和为16x+192.
(1)16x+192=1988,x=112,所以不可能;
(2)16x+192=1991,x=112,所以不可能;
(3)16x+192=2000,x=113,所以可能,最小数为113,最大数为137;
(4)16x+192=2080,x=118,所以可能,最小数为118,最大数为142.
分析:方程的思想是数学的另一个重要思想.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
