华师大版七年级数学下册10.1.2轴对称的再认识
文档属性
| 名称 | 华师大版七年级数学下册10.1.2轴对称的再认识 |

|
|
| 格式 | doc | ||
| 文件大小 | 202.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-21 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版七年级数学下册第十章轴对称、平移与旋转第1节轴对称
2轴对称的再认识同步练习
一、选择题
1. 已知正五边形的对称轴是过任意一个顶点与该顶点对边中点的直线.如图所示的正五边形中相邻两条对称轴所夹锐角α的度数为( )
A.75°
B.72°
C.70°
D.60°
答案:B
解析:解答:∵正五边形的中心角为:360°÷5=72°,
∴相邻两条对称轴所夹锐角α的度数为72°.
故选B.
分析:根据正五边形的性质与轴对称的性质,锐角α正好等于正五边形的中心角的度数,然后列式求解即可.
2. 若∠AOB=45°,P是∠AOB内一点,分别作点P关于直线OA、OB的对称点P1,P2,连接OP1,OP2,则下列结论正确的是( )
A.OP1⊥OP2
B.OP1=OP2
C.OP1≠OP2
D.OP1⊥OP2且OP1=OP2
答案:D
解析:解答:如图,∵点P关于直线OA、OB的对称点P1、P2,
∴OP1=OP2=OP,
∠AOP=∠AOP1,∠BOP=∠BOP2,
∴∠P1OP2=∠AOP+∠AOP1+∠BOP+∠BOP2,
=2(∠AOP+∠BOP),
=2∠AOB,
∵∠AOB=45°,
∴OP1⊥OP2成立.
故选D.
分析:根据轴对称的性质求出OP1、OP2的数量与夹角即可得解.
3. 下列图形中对称轴只有两条的是( )
A.
圆
B.
等边三角形
C.
矩形
D.
等腰梯形
答案:C
解析:解答:A、圆有无数条对称轴,故本选项错误;
B、等边三角形有3条对称轴,故本选项错误;
C、矩形有2条对称轴,故本选项正确;
D、等腰梯形有1条对称轴,故本选项错误;
故选:C.
分析:根据轴对称及对称轴的定义,结合所给图形即可作出判断.
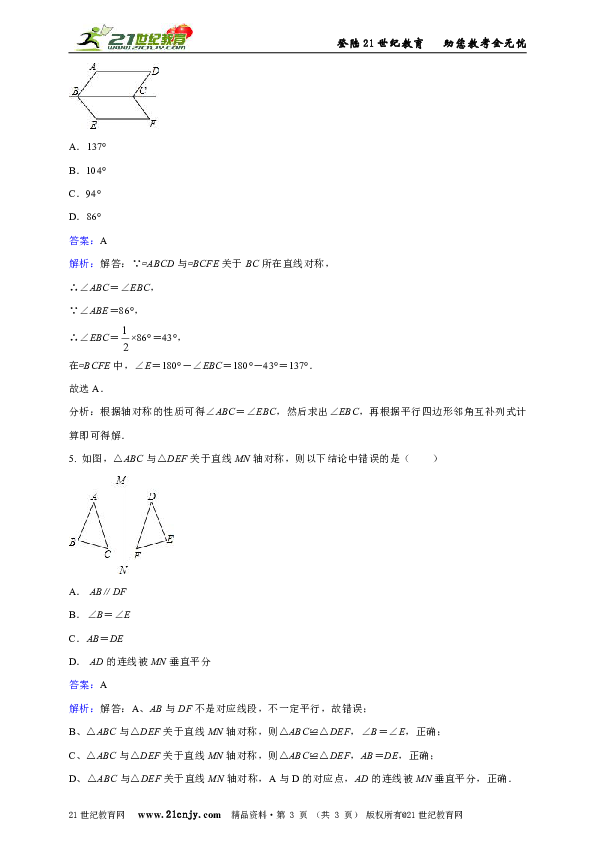
4. 如图,若 ABCD与 BCFE关于BC所在直线对称,∠ABE=86°,则∠E等于( )
A.137°
B.104°
C.94°
D.86°
答案:A
解析:解答:∵ ABCD与 BCFE关于BC所在直线对称,
∴∠ABC=∠EBC,
∵∠ABE=86°,
∴∠EBC=×86°=43°,
在 BCFE中,∠E=180°-∠EBC=180°-43°=137°.
故选A.
分析:根据轴对称的性质可得∠ABC=∠EBC,然后求出∠EBC,再根据平行四边形邻角互补列式计算即可得解.
5. 如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A. AB∥DF
B. ∠B=∠E
C. AB=DE
D. AD的连线被MN垂直平分
答案:A
解析:解答:A、AB与DF不是对应线段,不一定平行,故错误;
B、△ABC与△DEF关于直线MN轴对称,则△ABC≌△DEF,∠B=∠E,正确;
C、△ABC与△DEF关于直线MN轴对称,则△ABC≌△DEF,AB=DE,正确;
D、△ABC与△DEF关于直线MN轴对称,A与D的对应点,AD的连线被MN垂直平分,正确.
分析:根据轴对称的性质作答.
6. 下列说法中不正确的是( )
A.线段有1条对称轴
B.等边三角形有3条对称轴
C.角只有1条对称轴
D.底与腰不相等的等腰三角形只有一条对称轴
答案:A
解析:解答:线段有本身所在的直线和垂直平分线2条对称轴,A错误;
等边三角形有三条高所在的直线3条对称轴,B正确;
角只有角平分线所在的直线1条对称轴,C正确;
底与腰不相等的等腰三角形只有一条对称轴,D正确,
故选:A.
分析:根据轴对称图形的概念和具体图形确定各个选项中图形的对称轴,判断得到答案.
7. 下列图形中对称轴最多的是( )
A.等腰三角形
B.正方形
C.圆形
D.线段
答案:C
解析:解答:A、因为等腰三角形分别沿底边的中线所在的直线对折,对折后的两部分都能完全重合,则等腰三角形是轴对称图形,底边的中线所在的直线就是对称轴,所以等腰三角形有1条对称轴;
B、因为正方形沿对边的中线及其对角线所在的直线对折,对折后的两部分都能完全重合,则正方形是轴对称图形,对边的中线及其对角线所在的直线就是其对称轴,所以正方形有4条对称轴;
C、因为圆沿任意一条直径所在的直线对折,对折后的两部分都能完全重合,则圆是轴对称图形,任意一条直径所在的直线就是圆的对称轴,所以说圆有无数条对称轴.
D、线段是轴对称图形,有两条对称轴.
故选:C.
分析:依据轴对称图形的概念,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,据此即可进行选择.
8. 下列说法不正确的是( )
A.等边三角形有三条对称轴
B.线段AB只有一条对称轴
C.等腰三角形的对称轴是底边上的中线所在的直线
D.等腰三角形的对称轴是底边上的高所在的直线
答案:B
解析:解答:A、等边三角形有三条对称轴,故选项正确;
B、线段AB有线段AB本身所在的直线和线段AB的垂直平分线二条对称轴,故选项错误;
C、等腰三角形的对称轴是底边上的中线所在的直线,故选项正确;
D、等腰三角形的对称轴是底边上的高所在的直线,故选项正确.
故选B.
分析:根据对称轴的定义:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴.依此作答.
9. 正方形的对称轴的条数为( )
A.1
B.2
C.3
D.4
答案:D
解析:解答:正方形有4条对称轴.
故选:D.
分析:根据正方形的对称性解答.
10. 如图,直角坐标系中的五角星关于y轴对称的图形在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:A
解析:解答:如图所示,直角坐标系中的五角星关于y轴对称的图形在第一象限.
故选:A.
分析:根据轴对称的性质作出选择.
11. 如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为( )
A.30°
B.50°
C.90°
D.100°
答案:D
解析:解答:∵△ABC和△A′B′C′关于直线l对称,∠A=50°,∠C′=30°,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=30°,
∴∠B=180°-∠A-∠C=180°-50°-30°=100°.
故选D.
分析:先根据△ABC和△A′B′C′关于直线l对称得出△ABC≌△A′B′C′,故可得出∠C=∠C′,再由三角形内角和定理即可得出结论.
12. 如图,点A和点B相距60cm,且关于直线L对称,一只电动青蛙在与直线L相距20cm,与点A相距50cm的点P1处以A为对称中心跳至P2处,然后从P2处以L为对称轴跳至P3处,再从P3处以B为对称中心跳至P4处,再从P4处以L为对称轴跳至P5处,又从P5处以A为对称中心跳至P6处…,如此重复跳跃,则P2011与直线L的距离是( )
A.20cm
B.30cm
C.40cm
D.50cm
答案:C
解析:解答:如图,∵点A和点B相距60cm,
∴点A、B到直线l的距离为30cm,
∵点P1到直线l的距离为20cm,
∴点P2、P3到直线l得到距离为30×2-20=40cm,
由图可知,每4个点为一个循环组,∵2011÷4=502…3,
∴P2011与第三个点P3到直线L的距离相等为40cm.
故选C.
分析:作出图形,根据轴对称的性质可得点A、B到直线l的距离为30cm,再根据梯形的中位线等于两底边和的一半求出点P2、P3的距离,再根据规律判断出每4个点为一个循环组循环,然后用2011除以4,余数是几则与第几个点到直线l的距离相等.
13. 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠B=40゜,∠CAD=60゜,则∠BCD=( )
A.160゜
B.120゜
C.80゜
D.100゜
答案:A
解析:解答:根据轴对称的性质可得∠D=∠B=60°,
∵∠CAD=60゜,
∴∠DCA=180°-60°-40°=80°,
根据轴对称的性质可得∠BCA=∠DCA=80°,
∴∠BCD=160°,
故选:A.
分析:根据轴对称的性质可得∠D=∠B=60°,∠BCA=∠DCA,再根据∠DCA的度数,进而得到答案.
14. 已知,△ABC和△ADC关于直线AC轴对称,如果∠BAD+∠BCD=160°,那么△ABC是( )
A.直角三角形
B.等腰三角形
C.钝角三角形
D.锐角三角形
答案:C
解析:解答:如图,∵△ABC和△ADC关于直线AC轴对称,
∴∠BAC=∠DAC,∠ACB=∠ACD,
∴∠BAC+∠ACB=(∠BAD+∠BCD)=×160°=80°,
在△ABC中,∠B=180°-(∠BAC+∠ACB)=180°-80°=100°,
∴△ABC是钝角三角形.
故选C.
分析:作出图形,根据轴对称的性质可得∠BAC=∠DAC,∠ACB=∠ACD,然后求出∠BAC+∠ACB,再根据三角形的内角和定理求出∠B,然后判断三角形的形状即可.
15. 如图,直线m是多边形ABCDE的对称轴,其中∠A=120°,∠ABC=110°,那么∠BCD的度数为( )
A.50°
B.60°
C.70°
D.80°
答案:D
解析:解答:∵直线m是多边形ABCDE的对称轴,
∴∠E=∠A=120°,∠D=∠B=110°,
∴∠BCD=540°-120°×2-110°×2=80°.
故选:D.
分析:根据对称的性质,找出相等的角,再根据五边形的内角和即可求解.
二、填空题
16. 如图,如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=110°.那么∠BCD的度数等于________度.
答案:60°
解析:解答:把AE与直线m的交点记作F,
∵在四边形ABCF中,∠A=130°,∠B=110°,且直线m是多边形的对称轴;
∴∠BCD=2∠BCF=2×(360°-130°-110°-90°)=60°.
故填60°.
分析:根据轴对称图形的特点,且直线m把多边形ABCDE分成二个四边形,再根据四边形的内角和是360°,通过计算便可解决问题.
17. 如图,已知正方形的边长为4cm,则图中阴影部分的面积为________8cm2.
答案:8
解析:解答:根据图形的对称性,知:
阴影部分的面积=正方形的面积的一半.
故答案是:8.
分析:根据图形的对称性,则阴影部分的面积即为正方形的面积的一半.
18. 如图,△ABC的内部有一点P,且D、E、F是P分别以AB、BC、AC为对称轴的对称点.若△ABC的内角∠DAF=70°,∠DBE=60°,∠ECF=50°,则∠ADB+∠BEC+∠CFA=__________.
答案:360°
解析:解答:连接AP,BP,CP,
∵D,E,F是P分别以AB,BC,AC为对称轴的对称点
∴∠ADB=∠APB,∠BEC=∠BPC,∠CFA=∠APC,
∴∠ADB+∠BEC+∠CFA=∠APB+∠BPC+∠APC=360°.
故答案为:360°.
分析:连接AP,BP,CP后,根据轴对称的性质,可得到角相等,结合周角的定义可知答案.
19. 如图,∠A=29°,∠C′=62°,△ABC与△A′B′C′关于直线l对称,则∠B=_____89°
.
答案:89°
解析:解答:∵△ABC 与△A′B′C′关于直线l对称,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=62°,
∵∠A=29°,
∴∠B=180°-∠A-∠C=180°-29°-62°=89°.
故答案为:89°.
分析:先根据轴对称的性质得出△ABC≌△A′B′C′,由全等三角形的性质可知∠C=∠C′,再由三角形内角和定理可得出∠B的度数.
20. 如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的度数为________30
度.
答案:30°
解析:解答:∵∠B与∠E是对应角,∠B=30°,AF为对称轴,
∴∠E=∠B=30°.
故答案为:30°.
分析:由已知条件,根据轴对称图形的性质解答.
三、解答题
21. 如图,点P在∠AOB内,M、N分别是点P关于AO、BO的对称点,MN分别交AO,BO于点E、F,若△PEF的周长等于20cm,求MN的长.
答案:解答:∵M、N分别是点P关于AO、BO的对称点,
∴ME=PE,NF=PF,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∵△PEF的周长等于20cm,
∴MN=20cm.
解析:分析:根据轴对称的性质可得ME=PE,NF=PF,然后求出MN=△PEF的周长.
22. 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.
答案:解答::∵P点关于OA、OB的对称点P1,P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+MN+PN,
=P1M+MN+P2N,
=P1P2,
∵P1P2=10,
∴△PMN的周长=10.
解析:分析:根据轴对称的性质可得PM=P1M,PN=P2N,再求出△PMN的周长=P1P2,从而得解.
23. 如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
答案:解答:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,
∴∠G=360°-∠H-∠A-∠F=55°,
∴a=5cm b=4cm.
解析:分析:轴对称的性质:
(1)如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
24. 如图,△ABC和△A′B′C′关于直线m对称,
(1)结合图形指出对称点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样关系?
答案:解答::(1)由图可知,对称点有A和A′,B和B′,C和C′;
(2)连接AA′,直线m是线段AA′的垂直平分线;
(3)延长线段AC与A′C′,它们的交点在直线m上,其它对应线段(或其延长线)的交点也在直线m上,即若两线段关于直线m对称,且不平行,则它们的交点或其延长线的交点在对称轴上.
解析:分析:(1)根据图形找出找出对称点即可;
(2)、(3)根据轴对称的性质可直接得出结论.
25. 如图,∠A=90°,E为BC上的一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
答案:解答:∵A点和E点关于BD的对称,
∴∠ABD=∠EBD,
即∠ABC=2∠ABD=2∠DBE,
∵B点、C点关于DE对称,
∴∠C=∠DBC,
∴∠ABC=2∠C,
∵∠A=90°,
∴∠ABC+∠BCD=90°,
∴∠ABC=60°,∠C=30°.
解析:分析:根据轴对称的性质可得∠ABD=∠EBD,∠C=∠DBC,进而可得∠ABC=2∠ABD=2∠DBE,∠ABC=2∠C,再根据∠A=90°,可得∠ABC+∠BCD=90°,进而可得答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 2 页 (共 14 页) 版权所有@21世纪教育网
华师大版七年级数学下册第十章轴对称、平移与旋转第1节轴对称
2轴对称的再认识同步练习
一、选择题
1. 已知正五边形的对称轴是过任意一个顶点与该顶点对边中点的直线.如图所示的正五边形中相邻两条对称轴所夹锐角α的度数为( )
A.75°
B.72°
C.70°
D.60°
答案:B
解析:解答:∵正五边形的中心角为:360°÷5=72°,
∴相邻两条对称轴所夹锐角α的度数为72°.
故选B.
分析:根据正五边形的性质与轴对称的性质,锐角α正好等于正五边形的中心角的度数,然后列式求解即可.
2. 若∠AOB=45°,P是∠AOB内一点,分别作点P关于直线OA、OB的对称点P1,P2,连接OP1,OP2,则下列结论正确的是( )
A.OP1⊥OP2
B.OP1=OP2
C.OP1≠OP2
D.OP1⊥OP2且OP1=OP2
答案:D
解析:解答:如图,∵点P关于直线OA、OB的对称点P1、P2,
∴OP1=OP2=OP,
∠AOP=∠AOP1,∠BOP=∠BOP2,
∴∠P1OP2=∠AOP+∠AOP1+∠BOP+∠BOP2,
=2(∠AOP+∠BOP),
=2∠AOB,
∵∠AOB=45°,
∴OP1⊥OP2成立.
故选D.
分析:根据轴对称的性质求出OP1、OP2的数量与夹角即可得解.
3. 下列图形中对称轴只有两条的是( )
A.
圆
B.
等边三角形
C.
矩形
D.
等腰梯形
答案:C
解析:解答:A、圆有无数条对称轴,故本选项错误;
B、等边三角形有3条对称轴,故本选项错误;
C、矩形有2条对称轴,故本选项正确;
D、等腰梯形有1条对称轴,故本选项错误;
故选:C.
分析:根据轴对称及对称轴的定义,结合所给图形即可作出判断.
4. 如图,若 ABCD与 BCFE关于BC所在直线对称,∠ABE=86°,则∠E等于( )
A.137°
B.104°
C.94°
D.86°
答案:A
解析:解答:∵ ABCD与 BCFE关于BC所在直线对称,
∴∠ABC=∠EBC,
∵∠ABE=86°,
∴∠EBC=×86°=43°,
在 BCFE中,∠E=180°-∠EBC=180°-43°=137°.
故选A.
分析:根据轴对称的性质可得∠ABC=∠EBC,然后求出∠EBC,再根据平行四边形邻角互补列式计算即可得解.
5. 如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A. AB∥DF
B. ∠B=∠E
C. AB=DE
D. AD的连线被MN垂直平分
答案:A
解析:解答:A、AB与DF不是对应线段,不一定平行,故错误;
B、△ABC与△DEF关于直线MN轴对称,则△ABC≌△DEF,∠B=∠E,正确;
C、△ABC与△DEF关于直线MN轴对称,则△ABC≌△DEF,AB=DE,正确;
D、△ABC与△DEF关于直线MN轴对称,A与D的对应点,AD的连线被MN垂直平分,正确.
分析:根据轴对称的性质作答.
6. 下列说法中不正确的是( )
A.线段有1条对称轴
B.等边三角形有3条对称轴
C.角只有1条对称轴
D.底与腰不相等的等腰三角形只有一条对称轴
答案:A
解析:解答:线段有本身所在的直线和垂直平分线2条对称轴,A错误;
等边三角形有三条高所在的直线3条对称轴,B正确;
角只有角平分线所在的直线1条对称轴,C正确;
底与腰不相等的等腰三角形只有一条对称轴,D正确,
故选:A.
分析:根据轴对称图形的概念和具体图形确定各个选项中图形的对称轴,判断得到答案.
7. 下列图形中对称轴最多的是( )
A.等腰三角形
B.正方形
C.圆形
D.线段
答案:C
解析:解答:A、因为等腰三角形分别沿底边的中线所在的直线对折,对折后的两部分都能完全重合,则等腰三角形是轴对称图形,底边的中线所在的直线就是对称轴,所以等腰三角形有1条对称轴;
B、因为正方形沿对边的中线及其对角线所在的直线对折,对折后的两部分都能完全重合,则正方形是轴对称图形,对边的中线及其对角线所在的直线就是其对称轴,所以正方形有4条对称轴;
C、因为圆沿任意一条直径所在的直线对折,对折后的两部分都能完全重合,则圆是轴对称图形,任意一条直径所在的直线就是圆的对称轴,所以说圆有无数条对称轴.
D、线段是轴对称图形,有两条对称轴.
故选:C.
分析:依据轴对称图形的概念,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,据此即可进行选择.
8. 下列说法不正确的是( )
A.等边三角形有三条对称轴
B.线段AB只有一条对称轴
C.等腰三角形的对称轴是底边上的中线所在的直线
D.等腰三角形的对称轴是底边上的高所在的直线
答案:B
解析:解答:A、等边三角形有三条对称轴,故选项正确;
B、线段AB有线段AB本身所在的直线和线段AB的垂直平分线二条对称轴,故选项错误;
C、等腰三角形的对称轴是底边上的中线所在的直线,故选项正确;
D、等腰三角形的对称轴是底边上的高所在的直线,故选项正确.
故选B.
分析:根据对称轴的定义:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴.依此作答.
9. 正方形的对称轴的条数为( )
A.1
B.2
C.3
D.4
答案:D
解析:解答:正方形有4条对称轴.
故选:D.
分析:根据正方形的对称性解答.
10. 如图,直角坐标系中的五角星关于y轴对称的图形在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:A
解析:解答:如图所示,直角坐标系中的五角星关于y轴对称的图形在第一象限.
故选:A.
分析:根据轴对称的性质作出选择.
11. 如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为( )
A.30°
B.50°
C.90°
D.100°
答案:D
解析:解答:∵△ABC和△A′B′C′关于直线l对称,∠A=50°,∠C′=30°,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=30°,
∴∠B=180°-∠A-∠C=180°-50°-30°=100°.
故选D.
分析:先根据△ABC和△A′B′C′关于直线l对称得出△ABC≌△A′B′C′,故可得出∠C=∠C′,再由三角形内角和定理即可得出结论.
12. 如图,点A和点B相距60cm,且关于直线L对称,一只电动青蛙在与直线L相距20cm,与点A相距50cm的点P1处以A为对称中心跳至P2处,然后从P2处以L为对称轴跳至P3处,再从P3处以B为对称中心跳至P4处,再从P4处以L为对称轴跳至P5处,又从P5处以A为对称中心跳至P6处…,如此重复跳跃,则P2011与直线L的距离是( )
A.20cm
B.30cm
C.40cm
D.50cm
答案:C
解析:解答:如图,∵点A和点B相距60cm,
∴点A、B到直线l的距离为30cm,
∵点P1到直线l的距离为20cm,
∴点P2、P3到直线l得到距离为30×2-20=40cm,
由图可知,每4个点为一个循环组,∵2011÷4=502…3,
∴P2011与第三个点P3到直线L的距离相等为40cm.
故选C.
分析:作出图形,根据轴对称的性质可得点A、B到直线l的距离为30cm,再根据梯形的中位线等于两底边和的一半求出点P2、P3的距离,再根据规律判断出每4个点为一个循环组循环,然后用2011除以4,余数是几则与第几个点到直线l的距离相等.
13. 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠B=40゜,∠CAD=60゜,则∠BCD=( )
A.160゜
B.120゜
C.80゜
D.100゜
答案:A
解析:解答:根据轴对称的性质可得∠D=∠B=60°,
∵∠CAD=60゜,
∴∠DCA=180°-60°-40°=80°,
根据轴对称的性质可得∠BCA=∠DCA=80°,
∴∠BCD=160°,
故选:A.
分析:根据轴对称的性质可得∠D=∠B=60°,∠BCA=∠DCA,再根据∠DCA的度数,进而得到答案.
14. 已知,△ABC和△ADC关于直线AC轴对称,如果∠BAD+∠BCD=160°,那么△ABC是( )
A.直角三角形
B.等腰三角形
C.钝角三角形
D.锐角三角形
答案:C
解析:解答:如图,∵△ABC和△ADC关于直线AC轴对称,
∴∠BAC=∠DAC,∠ACB=∠ACD,
∴∠BAC+∠ACB=(∠BAD+∠BCD)=×160°=80°,
在△ABC中,∠B=180°-(∠BAC+∠ACB)=180°-80°=100°,
∴△ABC是钝角三角形.
故选C.
分析:作出图形,根据轴对称的性质可得∠BAC=∠DAC,∠ACB=∠ACD,然后求出∠BAC+∠ACB,再根据三角形的内角和定理求出∠B,然后判断三角形的形状即可.
15. 如图,直线m是多边形ABCDE的对称轴,其中∠A=120°,∠ABC=110°,那么∠BCD的度数为( )
A.50°
B.60°
C.70°
D.80°
答案:D
解析:解答:∵直线m是多边形ABCDE的对称轴,
∴∠E=∠A=120°,∠D=∠B=110°,
∴∠BCD=540°-120°×2-110°×2=80°.
故选:D.
分析:根据对称的性质,找出相等的角,再根据五边形的内角和即可求解.
二、填空题
16. 如图,如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=110°.那么∠BCD的度数等于________度.
答案:60°
解析:解答:把AE与直线m的交点记作F,
∵在四边形ABCF中,∠A=130°,∠B=110°,且直线m是多边形的对称轴;
∴∠BCD=2∠BCF=2×(360°-130°-110°-90°)=60°.
故填60°.
分析:根据轴对称图形的特点,且直线m把多边形ABCDE分成二个四边形,再根据四边形的内角和是360°,通过计算便可解决问题.
17. 如图,已知正方形的边长为4cm,则图中阴影部分的面积为________8cm2.
答案:8
解析:解答:根据图形的对称性,知:
阴影部分的面积=正方形的面积的一半.
故答案是:8.
分析:根据图形的对称性,则阴影部分的面积即为正方形的面积的一半.
18. 如图,△ABC的内部有一点P,且D、E、F是P分别以AB、BC、AC为对称轴的对称点.若△ABC的内角∠DAF=70°,∠DBE=60°,∠ECF=50°,则∠ADB+∠BEC+∠CFA=__________.
答案:360°
解析:解答:连接AP,BP,CP,
∵D,E,F是P分别以AB,BC,AC为对称轴的对称点
∴∠ADB=∠APB,∠BEC=∠BPC,∠CFA=∠APC,
∴∠ADB+∠BEC+∠CFA=∠APB+∠BPC+∠APC=360°.
故答案为:360°.
分析:连接AP,BP,CP后,根据轴对称的性质,可得到角相等,结合周角的定义可知答案.
19. 如图,∠A=29°,∠C′=62°,△ABC与△A′B′C′关于直线l对称,则∠B=_____89°
.
答案:89°
解析:解答:∵△ABC 与△A′B′C′关于直线l对称,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=62°,
∵∠A=29°,
∴∠B=180°-∠A-∠C=180°-29°-62°=89°.
故答案为:89°.
分析:先根据轴对称的性质得出△ABC≌△A′B′C′,由全等三角形的性质可知∠C=∠C′,再由三角形内角和定理可得出∠B的度数.
20. 如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的度数为________30
度.
答案:30°
解析:解答:∵∠B与∠E是对应角,∠B=30°,AF为对称轴,
∴∠E=∠B=30°.
故答案为:30°.
分析:由已知条件,根据轴对称图形的性质解答.
三、解答题
21. 如图,点P在∠AOB内,M、N分别是点P关于AO、BO的对称点,MN分别交AO,BO于点E、F,若△PEF的周长等于20cm,求MN的长.
答案:解答:∵M、N分别是点P关于AO、BO的对称点,
∴ME=PE,NF=PF,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∵△PEF的周长等于20cm,
∴MN=20cm.
解析:分析:根据轴对称的性质可得ME=PE,NF=PF,然后求出MN=△PEF的周长.
22. 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.
答案:解答::∵P点关于OA、OB的对称点P1,P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+MN+PN,
=P1M+MN+P2N,
=P1P2,
∵P1P2=10,
∴△PMN的周长=10.
解析:分析:根据轴对称的性质可得PM=P1M,PN=P2N,再求出△PMN的周长=P1P2,从而得解.
23. 如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
答案:解答:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,
∴∠G=360°-∠H-∠A-∠F=55°,
∴a=5cm b=4cm.
解析:分析:轴对称的性质:
(1)如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
24. 如图,△ABC和△A′B′C′关于直线m对称,
(1)结合图形指出对称点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样关系?
答案:解答::(1)由图可知,对称点有A和A′,B和B′,C和C′;
(2)连接AA′,直线m是线段AA′的垂直平分线;
(3)延长线段AC与A′C′,它们的交点在直线m上,其它对应线段(或其延长线)的交点也在直线m上,即若两线段关于直线m对称,且不平行,则它们的交点或其延长线的交点在对称轴上.
解析:分析:(1)根据图形找出找出对称点即可;
(2)、(3)根据轴对称的性质可直接得出结论.
25. 如图,∠A=90°,E为BC上的一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
答案:解答:∵A点和E点关于BD的对称,
∴∠ABD=∠EBD,
即∠ABC=2∠ABD=2∠DBE,
∵B点、C点关于DE对称,
∴∠C=∠DBC,
∴∠ABC=2∠C,
∵∠A=90°,
∴∠ABC+∠BCD=90°,
∴∠ABC=60°,∠C=30°.
解析:分析:根据轴对称的性质可得∠ABD=∠EBD,∠C=∠DBC,进而可得∠ABC=2∠ABD=2∠DBE,∠ABC=2∠C,再根据∠A=90°,可得∠ABC+∠BCD=90°,进而可得答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 2 页 (共 14 页) 版权所有@21世纪教育网
