2025年中考数学培优模型八 折叠模型(含解析)
文档属性
| 名称 | 2025年中考数学培优模型八 折叠模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 281.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 13:41:11 | ||
图片预览


文档简介
模型八 折叠模型
类型 ①矩形中的折叠(省模考22题)
例1 [2023 盘锦18题3分]如图,四边形ABCD 是矩形,AB= ,BC=6,点E 为边 BC的中点,点F 为边AD上一点,将四边形ABEF沿EF折叠,点A 的对应点为点, ,点B 的对应点为点 B',过点 B'作B'H⊥BC 于点 H,若 ,则 FD 的长是 .
【点拨】设B'E交AD 于点 G,根据折叠的性质可知BE=B'E,∠BEF=∠B'EF,根据平行线的性质可得∠GFE=∠BEF,∴∠GFE=∠B'EF,∴FG=EG,利用勾股定理求出EH的值;过点E作EM⊥AD 于点M,易证△EMG∽△B'HE,利用相似三角形的性质及线段和差关系可求出AF的值,再根据FD=AD-AF进行计算即可得到答案.
模型总结
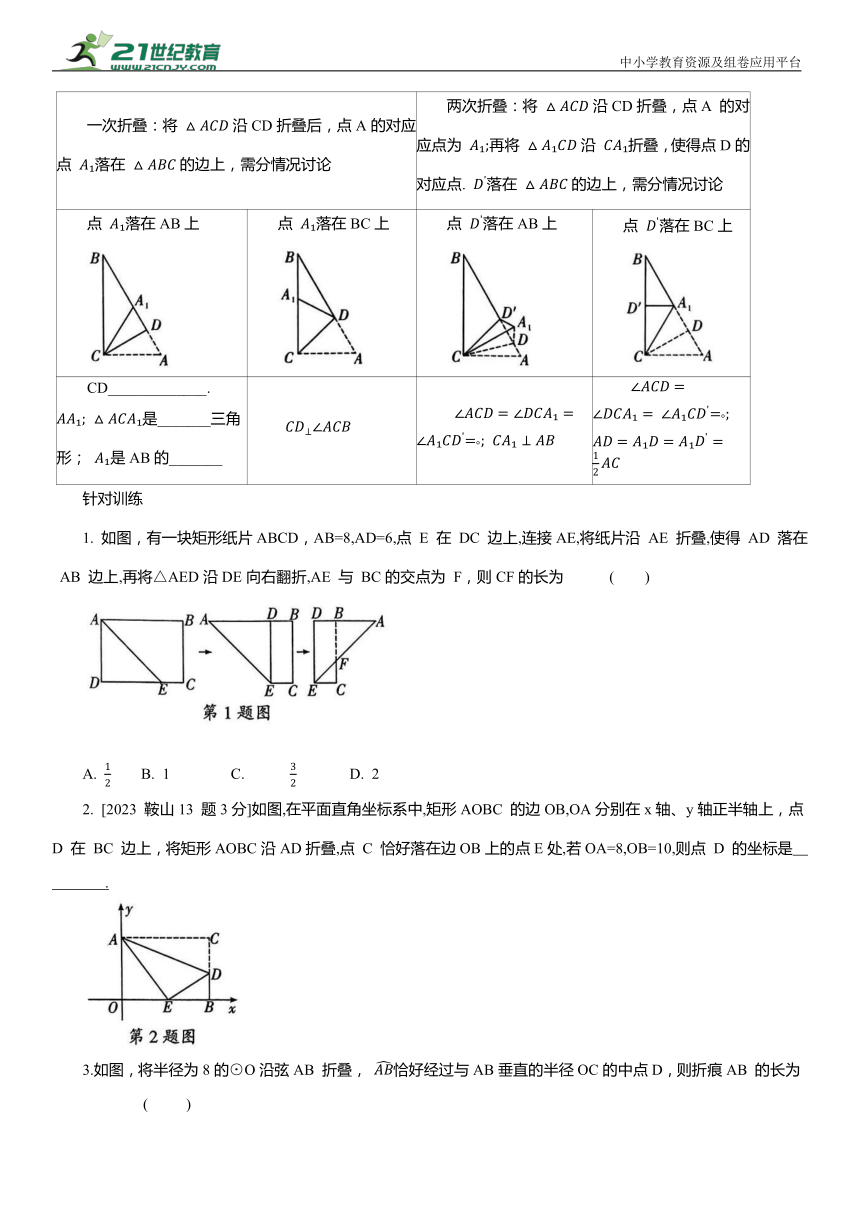
图形 结论
点B'在矩形ABCD 内部(折痕CP) ①BP=_____,BC=________=AD; ②∠B=∠PB'C,∠BPC=∠B'PC,∠BCP=∠B'CP; ③△BPC_____△B'PC; ④△AB'P∽△ABC
点B'在矩形ABCD 边上(折痕CP) ①BP=_______,BC=_______=AD; ②∠B=∠PB'C,∠BPC=∠B'PC,∠BCP=∠B'CP; ③△BPC≌△B'PC; ⑤直角三角形(常用勾股定理):Rt△DB'C,Rt△AB'P
点B'在矩形 ABCD 外部(折痕CA) ①AB=______,BC=_______=AD; ②∠B=∠B',∠BAC=∠B'AC,∠BCA=∠B'CA; ③△BAC≌△B'AC,△CDF≌△AB'F; ④直角三角形(常用勾股定理):Rt△AB'F,Rt△CDF
续表点B 与点 D 重合(折痕 EF) ①四边形 BFDE 是_______; ②A',F,B三点共线; ③点A,B,C,D,A'在同一个圆上; ④直角三角形(常用勾股定理):
两次折叠(折痕AG,GE) ①A,F,E三点共线; ,即点G为_的中点;
类型 三角形中的折叠(真卷22题)
例2 [2024辽宁二模]如图,在等腰Rt△ABC中,AC=BC=4,∠C=90°,D为边AC 的中点,E为边AB上的一个动点,连接DE,将△ABC沿DE 折叠,点A的对应点为 ,当A'E⊥AC时,BE 的长度为 .
【点拨】此题需注意进行分类讨论.设直线A'E交AC 于点 F,①当点F 在点D下方时,由题意可得AB=4 ,∠A=45°,结合折叠的性质及A'E⊥AC,可推出△AEF,△A'DF都是等腰直角三角形,从而得到 DF,可得 利用BE=AB-AE 即可求解;②当点F在点D上方时,同理可得.
模型总结
在 中, ,D 是AB 上一点
一次折叠:将 沿CD折叠后,点A的对应点 落在 的边上,需分情况讨论 两次折叠:将 沿CD折叠,点A 的对应点为 再将 沿 折叠,使得点D的对应点. 落在 的边上,需分情况讨论
点 落在AB上 点 落在BC上 点 落在AB上 点 落在BC上
CD_____________. 是_______三角形; 是AB的_______
针对训练
1. 如图,有一块矩形纸片ABCD,AB=8,AD=6,点 E 在 DC 边上,连接AE,将纸片沿 AE 折叠,使得 AD 落在 AB 边上,再将△AED沿DE向右翻折,AE 与 BC的交点为 F,则CF的长为 ( )
A. B. 1 C. D. 2
2. [2023 鞍山13 题3分]如图,在平面直角坐标系中,矩形AOBC 的边OB,OA分别在x轴、y轴正半轴上,点D 在 BC 边上,将矩形AOBC沿AD折叠,点 C 恰好落在边OB上的点E处,若OA=8,OB=10,则点 D 的坐标是 .
3.如图,将半径为8的⊙O沿弦AB 折叠, 恰好经过与AB垂直的半径OC的中点D,则折痕AB 的长为 ( )
C. 8 D. 10
4.[2024 盘锦兴隆台区期末]如图,在等边三角形ABC中,点 D,E分别为AB,AC边上一点,连接DE,将△AED沿DE 折叠,点A恰好落在BC边的点 F处,若AD:AE=2:3,且 则,S△ECF= .
5.如图,将一张三角形纸片ABC 的一角折叠,使得点A 落在四边形 BCDE 的外部点A'的位置,且点A'与点 C 在直线AB 的异侧,折痕为DE,已知∠C=90°,∠A=34°.若保持△A'DE 的一边与 BC 平行,则∠ADE 的度数为 .
6. [2024 沈阳和平区月考]在 Rt△ABC 中,∠C=90°,AC=6,点D 为边BC上一点,将△ACD 沿直线 AD 翻折得到△AED,点 C的对应点为点 E,连接BE,如果△BDE是以BD为直角边的等腰直角三角形,那么BC的长等于 .
7.[2024朝阳月考]如图,在矩形ABCD中,点E在边 BC上,将△ABE 沿AE 折叠后,点 B 的对应点落在对角线AC 上的点 F处.若OF= 则BE 的长是 .
中小学教育资源及组卷应用平台
模型八 折叠模型
例1 3+ 【解析】如解图,设B'E 交AD 于点G,过点E作EM⊥AD 于点M,则∠AME=90°,∵点E为边BC的中点,∴ ∴四边形ABCD 为矩形,BC=6,∴AD=BC=6,∠A=∠B=90°,AD∥BC,∴∠AME=∠A=∠B=90°,∴四边形ABEM 为矩形,∴ M=BE=3,由折叠可知,B'E=BE=3,∠BEF=∠B'EF,∵AD∥BC,∴∠GFE=∠BEF,∴∠GFE=∠B'EF,∴FG=EG,∵B'H⊥BC,∴∠B'HE=90°,在Rt△B'HE中,EH= ∴∠EMG=∠B'HE=90°,∵AD∥BC,∴∠EGM=∠B'EH,∴△EMG∽△B'HE,∴EGE=MG=E=BMH,貝 ∴AF=AM-FM=3- ,∴FD=AD-AF=6-(3-
【模型总结】
B'P B'C ≌ B'P B'C AB' B'C 菱形 BC 90
例2 2 -2或2 +2 【解析】设直线A'E交AC于点 F,①当点F在点 D 下方时,如解图①,∵AC=BC=4,∠C=90°,∴AB=4 ,∠A=45°,∵将△ABC 沿 DE 折叠,点A的对应点为点A',D 为边AC的中点,∴∠A'=∠A=45°,
AD=A'D=2,∵A'E⊥AC,∴△AEF,△A'DF都是等腰直角三角形,∴ ②当点F在点 D 上方时,如解图②,同理可得A'D=AD= 2 -2,∴BE=AB-AE=2 +2.综上所述,BE 的长为2 -2或
【模型总结】
垂直平分 等边 中点 平分 15 30
【针对训练】
1. D 2. (10,3) 3. B 4. 4.5 5. 45°或28°
6. 12或3
7. 【解析】设 BE=3m,∵四边形 ABCD 是矩形,∴OA=OC= AC,OB=OD= BD,AC=BD,∠ABC=90°,∴OC=OB,∴∠ACB=∠DBC,由折叠得 FE=BE=3m,∠AFE=∠ABE=90°,∴∠EFC=180°-∠AFE=90°,∴BC=FE= =1+4m,BC=BE+CE=3m+5m=8m,∴4(1+4m)=3×8m,解得
类型 ①矩形中的折叠(省模考22题)
例1 [2023 盘锦18题3分]如图,四边形ABCD 是矩形,AB= ,BC=6,点E 为边 BC的中点,点F 为边AD上一点,将四边形ABEF沿EF折叠,点A 的对应点为点, ,点B 的对应点为点 B',过点 B'作B'H⊥BC 于点 H,若 ,则 FD 的长是 .
【点拨】设B'E交AD 于点 G,根据折叠的性质可知BE=B'E,∠BEF=∠B'EF,根据平行线的性质可得∠GFE=∠BEF,∴∠GFE=∠B'EF,∴FG=EG,利用勾股定理求出EH的值;过点E作EM⊥AD 于点M,易证△EMG∽△B'HE,利用相似三角形的性质及线段和差关系可求出AF的值,再根据FD=AD-AF进行计算即可得到答案.
模型总结
图形 结论
点B'在矩形ABCD 内部(折痕CP) ①BP=_____,BC=________=AD; ②∠B=∠PB'C,∠BPC=∠B'PC,∠BCP=∠B'CP; ③△BPC_____△B'PC; ④△AB'P∽△ABC
点B'在矩形ABCD 边上(折痕CP) ①BP=_______,BC=_______=AD; ②∠B=∠PB'C,∠BPC=∠B'PC,∠BCP=∠B'CP; ③△BPC≌△B'PC; ⑤直角三角形(常用勾股定理):Rt△DB'C,Rt△AB'P
点B'在矩形 ABCD 外部(折痕CA) ①AB=______,BC=_______=AD; ②∠B=∠B',∠BAC=∠B'AC,∠BCA=∠B'CA; ③△BAC≌△B'AC,△CDF≌△AB'F; ④直角三角形(常用勾股定理):Rt△AB'F,Rt△CDF
续表点B 与点 D 重合(折痕 EF) ①四边形 BFDE 是_______; ②A',F,B三点共线; ③点A,B,C,D,A'在同一个圆上; ④直角三角形(常用勾股定理):
两次折叠(折痕AG,GE) ①A,F,E三点共线; ,即点G为_的中点;
类型 三角形中的折叠(真卷22题)
例2 [2024辽宁二模]如图,在等腰Rt△ABC中,AC=BC=4,∠C=90°,D为边AC 的中点,E为边AB上的一个动点,连接DE,将△ABC沿DE 折叠,点A的对应点为 ,当A'E⊥AC时,BE 的长度为 .
【点拨】此题需注意进行分类讨论.设直线A'E交AC 于点 F,①当点F 在点D下方时,由题意可得AB=4 ,∠A=45°,结合折叠的性质及A'E⊥AC,可推出△AEF,△A'DF都是等腰直角三角形,从而得到 DF,可得 利用BE=AB-AE 即可求解;②当点F在点D上方时,同理可得.
模型总结
在 中, ,D 是AB 上一点
一次折叠:将 沿CD折叠后,点A的对应点 落在 的边上,需分情况讨论 两次折叠:将 沿CD折叠,点A 的对应点为 再将 沿 折叠,使得点D的对应点. 落在 的边上,需分情况讨论
点 落在AB上 点 落在BC上 点 落在AB上 点 落在BC上
CD_____________. 是_______三角形; 是AB的_______
针对训练
1. 如图,有一块矩形纸片ABCD,AB=8,AD=6,点 E 在 DC 边上,连接AE,将纸片沿 AE 折叠,使得 AD 落在 AB 边上,再将△AED沿DE向右翻折,AE 与 BC的交点为 F,则CF的长为 ( )
A. B. 1 C. D. 2
2. [2023 鞍山13 题3分]如图,在平面直角坐标系中,矩形AOBC 的边OB,OA分别在x轴、y轴正半轴上,点D 在 BC 边上,将矩形AOBC沿AD折叠,点 C 恰好落在边OB上的点E处,若OA=8,OB=10,则点 D 的坐标是 .
3.如图,将半径为8的⊙O沿弦AB 折叠, 恰好经过与AB垂直的半径OC的中点D,则折痕AB 的长为 ( )
C. 8 D. 10
4.[2024 盘锦兴隆台区期末]如图,在等边三角形ABC中,点 D,E分别为AB,AC边上一点,连接DE,将△AED沿DE 折叠,点A恰好落在BC边的点 F处,若AD:AE=2:3,且 则,S△ECF= .
5.如图,将一张三角形纸片ABC 的一角折叠,使得点A 落在四边形 BCDE 的外部点A'的位置,且点A'与点 C 在直线AB 的异侧,折痕为DE,已知∠C=90°,∠A=34°.若保持△A'DE 的一边与 BC 平行,则∠ADE 的度数为 .
6. [2024 沈阳和平区月考]在 Rt△ABC 中,∠C=90°,AC=6,点D 为边BC上一点,将△ACD 沿直线 AD 翻折得到△AED,点 C的对应点为点 E,连接BE,如果△BDE是以BD为直角边的等腰直角三角形,那么BC的长等于 .
7.[2024朝阳月考]如图,在矩形ABCD中,点E在边 BC上,将△ABE 沿AE 折叠后,点 B 的对应点落在对角线AC 上的点 F处.若OF= 则BE 的长是 .
中小学教育资源及组卷应用平台
模型八 折叠模型
例1 3+ 【解析】如解图,设B'E 交AD 于点G,过点E作EM⊥AD 于点M,则∠AME=90°,∵点E为边BC的中点,∴ ∴四边形ABCD 为矩形,BC=6,∴AD=BC=6,∠A=∠B=90°,AD∥BC,∴∠AME=∠A=∠B=90°,∴四边形ABEM 为矩形,∴ M=BE=3,由折叠可知,B'E=BE=3,∠BEF=∠B'EF,∵AD∥BC,∴∠GFE=∠BEF,∴∠GFE=∠B'EF,∴FG=EG,∵B'H⊥BC,∴∠B'HE=90°,在Rt△B'HE中,EH= ∴∠EMG=∠B'HE=90°,∵AD∥BC,∴∠EGM=∠B'EH,∴△EMG∽△B'HE,∴EGE=MG=E=BMH,貝 ∴AF=AM-FM=3- ,∴FD=AD-AF=6-(3-
【模型总结】
B'P B'C ≌ B'P B'C AB' B'C 菱形 BC 90
例2 2 -2或2 +2 【解析】设直线A'E交AC于点 F,①当点F在点 D 下方时,如解图①,∵AC=BC=4,∠C=90°,∴AB=4 ,∠A=45°,∵将△ABC 沿 DE 折叠,点A的对应点为点A',D 为边AC的中点,∴∠A'=∠A=45°,
AD=A'D=2,∵A'E⊥AC,∴△AEF,△A'DF都是等腰直角三角形,∴ ②当点F在点 D 上方时,如解图②,同理可得A'D=AD= 2 -2,∴BE=AB-AE=2 +2.综上所述,BE 的长为2 -2或
【模型总结】
垂直平分 等边 中点 平分 15 30
【针对训练】
1. D 2. (10,3) 3. B 4. 4.5 5. 45°或28°
6. 12或3
7. 【解析】设 BE=3m,∵四边形 ABCD 是矩形,∴OA=OC= AC,OB=OD= BD,AC=BD,∠ABC=90°,∴OC=OB,∴∠ACB=∠DBC,由折叠得 FE=BE=3m,∠AFE=∠ABE=90°,∴∠EFC=180°-∠AFE=90°,∴BC=FE= =1+4m,BC=BE+CE=3m+5m=8m,∴4(1+4m)=3×8m,解得
同课章节目录
