2025年中考数学培优模型九 几何图形最值模型(含解析)
文档属性
| 名称 | 2025年中考数学培优模型九 几何图形最值模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 396.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 13:41:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
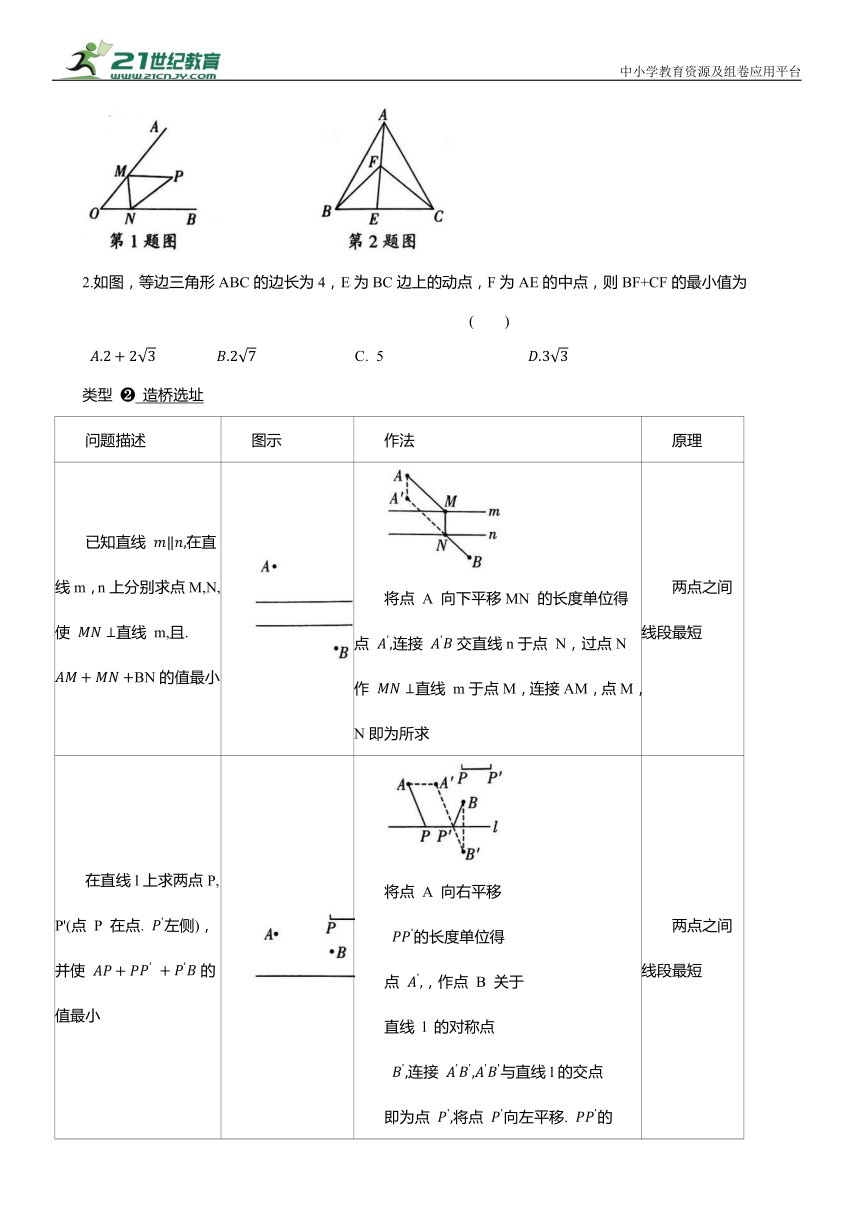
模型九 几何图形最值模型
类型 ① 将军饮马
模型 图示 作法 原理
点 A,B 在直线l异侧 连接AB 交直线 l 于点 P,点 P 即为所求作的点 两点之间线段最短
点 A,B 在直线l同侧 作点A关于直线l的对称点; 连接 交直线l于点P,点P即为所求作的点
例1 如图,正方形ABCD的边长为8,点 M 在 CD上,且 ,N是AC上的一个动点,则DN+MN的最小值为 ( )
A. 6 B. 8 C. 10
针对训练
1. 如图,已知. 点P 为. 内部一点,点M 为射线OA、点N 为射线OB上的两个动点,当 的周长最小时,则
2.如图,等边三角形ABC的边长为4,E为BC边上的动点,F为AE的中点,则BF+CF的最小值为 ( )
C. 5
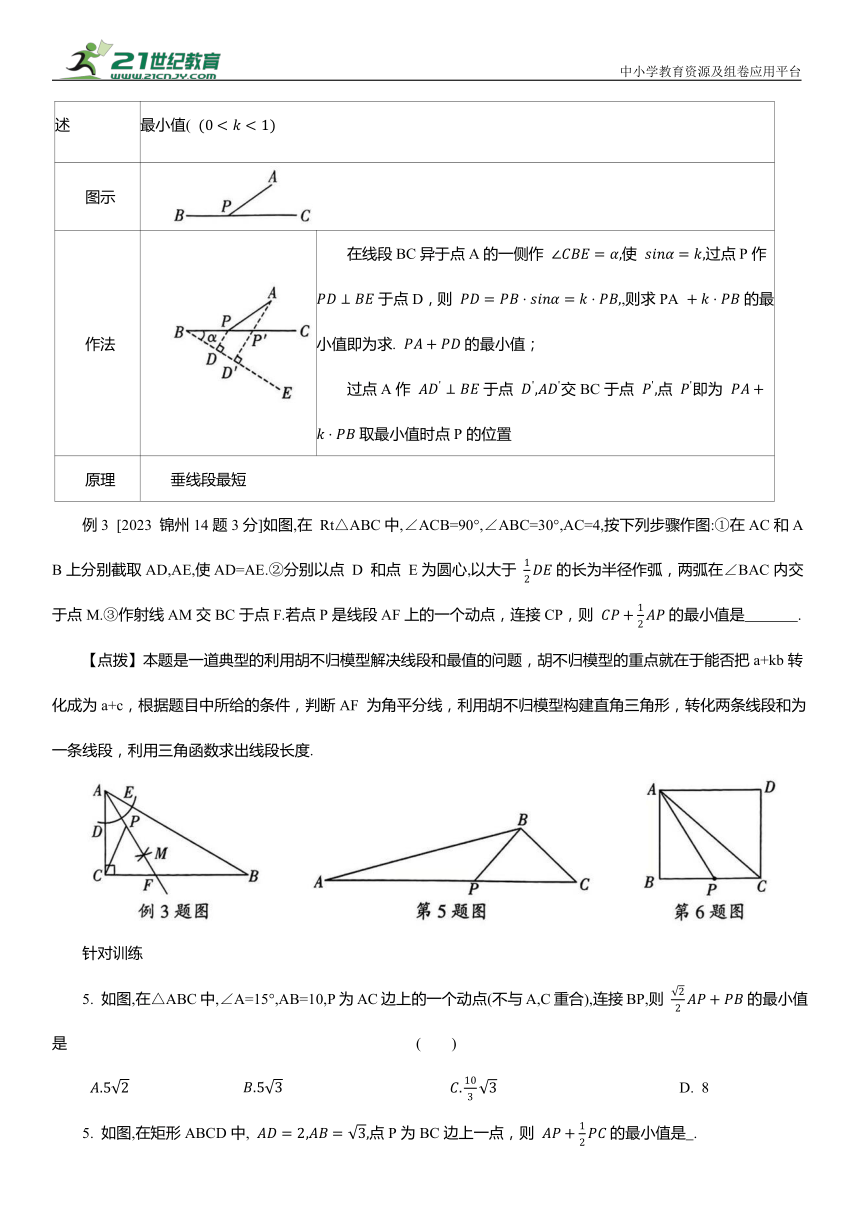
类型 造桥选址
问题描述 图示 作法 原理
已知直线 在直线m,n上分别求点M,N,使 直线 m,且. BN的值最小 将点 A 向下平移MN 的长度单位得点 连接 交直线n于点 N,过点N 作 直线 m于点M,连接AM,点M,N即为所求 两点之间线段最短
在直线l上求两点P,P'(点 P 在点. 左侧),并使 的值最小 将点 A 向右平移 的长度单位得 点 ,作点 B 关于 直线 l 的对称点 连接 与直线l的交点 即为点 将点 向左平移. 的 长度单位即为点P 两点之间线段最短
例2 人、、上P86问题2改编]已知A地和B地在一条河的两岸(河岸平行),现要在河上建一座垂直于河岸的桥 MN,请在图中找到合适的建桥位置,使从A 地到 B 地的路径. MN+NB 最短.
【自主作图】
【点拨】利用两点之间线段最短进行求解,要使 最短,即为求解. 的最小值
①将点A 沿着垂直于河岸b的方向平移到点. 使得
②连接 交河岸b于点N,
③过点N作 ,交河岸a于点M,连接AM,可以发现此时 即
针对训练
3. [2023鞍山月考]如图,在平面直角坐标系中,已知A(3,6),B(-2,2),在x轴上取两点C,D(点C在点D 左侧),且始终保持( ,线段CD在x轴上平移,当. 的值最小时,点C 的坐标为 .
如图,在矩形ABCD中, G是AD的中点,线段 EF 在边 AB 上左右滑动,连接GE,CF,若 则 的最小值为 .
类型3 胡不归
问题描述 已知点P 是线段BC 上一动点,点A 是直线BC 外一定点,连接PA,求, k·PB的最小值(
图示
作法 在线段BC异于点A的一侧作 使 过点P作 于点D,则 ,则求PA 的最小值即为求. 的最小值; 过点A作 于点 交BC于点 点 即为 取最小值时点P的位置
原理 垂线段最短
例3 [2023 锦州14题3分]如图,在 Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,按下列步骤作图:①在AC和AB上分别截取AD,AE,使AD=AE.②分别以点 D 和点 E为圆心,以大于 的长为半径作弧,两弧在∠BAC内交于点M.③作射线AM交BC于点F.若点P是线段AF上的一个动点,连接CP,则 的最小值是 .
【点拨】本题是一道典型的利用胡不归模型解决线段和最值的问题,胡不归模型的重点就在于能否把a+kb转化成为a+c,根据题目中所给的条件,判断AF 为角平分线,利用胡不归模型构建直角三角形,转化两条线段和为一条线段,利用三角函数求出线段长度.
针对训练
5. 如图,在△ABC中,∠A=15°,AB=10,P为AC边上的一个动点(不与A,C重合),连接BP,则 的最小值是 ( )
D. 8
如图,在矩形ABCD中, 点P为BC边上一点,则 的最小值是 .
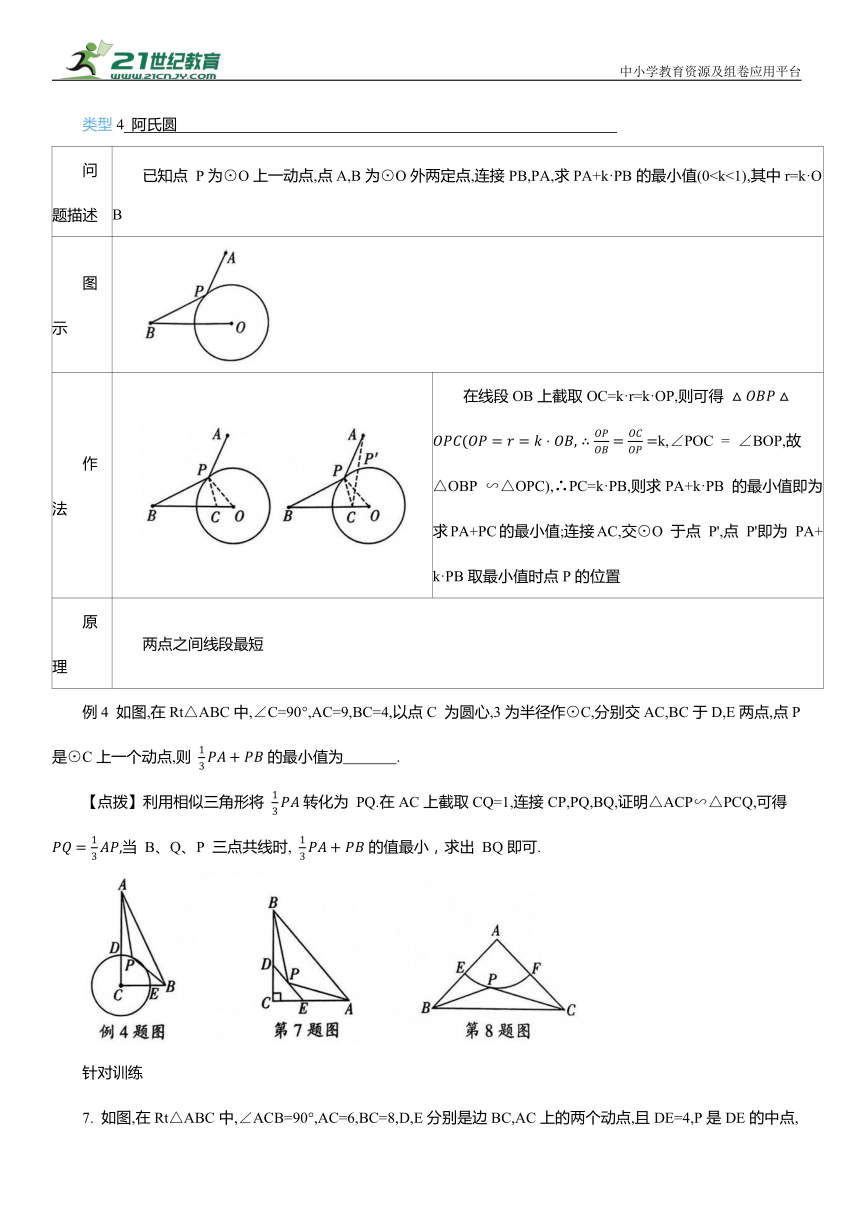
类型4 阿氏圆
问题描述 已知点 P为⊙O上一动点,点A,B为⊙O外两定点,连接PB,PA,求PA+k·PB的最小值(0图示
作法 在线段OB上截取OC=k·r=k·OP,则可得 k,∠POC = ∠BOP,故 △OBP ∽△OPC),∴PC=k·PB,则求PA+k·PB 的最小值即为求PA+PC的最小值;连接AC,交⊙O 于点 P',点 P'即为 PA+k·PB取最小值时点P的位置
原理 两点之间线段最短
例4 如图,在Rt△ABC中,∠C=90°,AC=9,BC=4,以点C 为圆心,3为半径作⊙C,分别交AC,BC于D,E两点,点P 是⊙C上一个动点,则 的最小值为 .
【点拨】利用相似三角形将 转化为 PQ.在AC上截取CQ=1,连接CP,PQ,BQ,证明△ACP∽△PCQ,可得 当 B、Q、P 三点共线时, 的值最小,求出 BQ即可.
针对训练
7. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D,E分别是边BC,AC上的两个动点,且DE=4,P是DE的中点,连接PA,PB,则 的最小值为 .
.如图,在△ABC中,∠A=90°,AB=AC=4,点E,F分别是边AB,AC的中点,点 P 是以A为圆心、以AE长为半径的圆弧上的动点,则 的最小值为 .
类型 费马点
问题描述 图示 思路 作法 原理
在 任 意 内确定一点P,使得PA 最小 将以 P 为顶点的三角形旋转 得到等边三角形,则三条共顶点(点P)线段转化为首尾相连的折线段 将 绕点B顺时针旋转 得到 连接 得到等边三角形. 则 当 PA, 和 在一条直线上时, 最小 两点之间线段最短
例5 如果点P 是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫 的费马点.已经证明:在三个内角均小于120°的△ABC 中,当∠APB=∠APC=∠BPC=120°时,点P 就是△ABC的费马点.若点 P 是腰长为 的等腰直角三角形DEF的费马点,则PD+PE+PF= .
【点拨】过点D作DM⊥EF 于点M,在△DEF 内部过E,F分别作∠ ,结合费马点的定义,求出 PE,PF,DP的长即可解决问题.
针对训练
9.如图,等边△ABC的边长为1,AF为BC边上的高,点D,E分别为AC,AF上的两个动点,且满足CD=AE,则BD+CE的最小值为 ( )
A. 1
10. 组合练 如图,D是等边三角形ABC 外一点,连接AD,BD,CD,已知. 则当线段AD的长度最小时.
(1)∠BDC= ;
(2)AD 的最小值是 .
模型九 几何图形最值模型
例1 C
【针对训练】
1.80° 【解析】如解图,作点P 关于OB 的对称点 E,连接EO,EM,∴EM=MP,∠MPO=∠OEM,∠EOM=∠MOP,作点 P 关于OA 的对称点 F,连接 NF,OF,∴ PN=FN,∠OPN=∠OFN,∠PON=∠NOF,∴PM+PN+MN=EM+NF+MN≥EF,∴当E,M,N,F四点共线时,△PMN周长最小,又∵ ∠EOF=∠EOM+∠MOP+∠PON+∠NOF,∠AOB=∠MOP+∠PON,∴∠EOF=2∠AOB,又∵∠AOB=50°,∴∠EOF=100°,∵在△EOF中,∠OEM+∠OFN+∠EOF=180°,∴ ∠OEM+∠OFN=180°-100°=80°,∵∠MPO=∠OEM,∠OPN=∠OFN,∴∠MPO+∠OPN=80°,即∠MPN=80°.
2. B 【解析】如解图,分别取AB,AC 的中点M,N,作直线MN、由三角形中位线定理知MN与AE的交点为AE的中点F,即点 F 是直线 MN上的一个动点,作点 B 关于 MN的对称点B',连接B'C,B'F,则B'F=BF,∴BF+CF=B'F+CF≥B'C,∴BF+CF的最小值为B'C的长,由题意知BC=4,则等边△ABC中,BC边上的高为2 ,∴B'B=2 在 Rt△B'CB 中, 2
例2 解:桥MN的位置如解图所示.
3.(-1,0) 【解析】如解图,把A(3,6)向左平移1个单位长度得A'(2,6),作点B关于x轴的对称点 B',连接B'A'交x轴于点C,在x轴上取点D(点C 在点 D 左侧),使CD=1,连接AD,此时AD+BC的值最小,∵B(-2,2),∴B'(-2,-2),设直线 B'A'的解析式为 y= kx+b,∴ 解得 直线 B'A'的解析式为y=2x+2,当y=0时,x=-1,∴C(-1,0).
4.3 【解析】解法1:如解图①,作点G关于AB的对称点G',在CD上截取CH=1,连接HG'交AB 于点 E,在EB上截取EF=1,则GE=G'E,此时GE+CF的值最小,∵ CH=EF=1,CH∥EF,∴四边形EFCH是平行四边形,∴EH=CF,∴ G'H=EG'+EH=EG+CF,∵AB=4,BC=AD=2,G为边AD的中点,∴DG'=AD+AG'=2+1=3,DH=4-1=3,在Rt△G'DH中,由勾股定理得 即GE+CF的最小值为3
解法2:如解图①, 设AE=x,则.BF=AB-EF-AE=4-x-1=3-x,E由勾股定理得 EG+CF= 如解图②,在矩形 MNKR 中,MR=3,KR=2,KQ=1,P为NK上一动点,设 PK=y,则 由解图②可知,当M,P,Q 三点共线时,MP+PQ 最小,最小值是3 ,即EG+CF 的最小值是3
例3 2 5. B
6. 【解析】如解图,在矩形外作∠BCM=30°,过点 P作PE⊥CM,则 过点A作AF⊥CM于点 F,交 BC于点 P', 的最小值为 AF 的长,∵∠AP'B=∠CP'F=90°-∠BCM=60°,
∠B=90°,在 Rt△ABP'中, 在Rt△CFP'中,
例4
【针对训练】
【解析】如解图,在CB 上取一点 F,使得 连接PF,AF,PC.∵∠DCE=90°,DE=4,P 为DE的中点, =∠BCP,∴△PCF∽△BCP,∴PF=CF= ,∴PF = ∴当F,P,A三点共线时 的值最小,在 Rt△ACF 中, 的最小值为
8. 【解析】如解图,在AB上截取AQ=1,连接AP,PQ,CQ,∵点E,F分别是边AB,AC 的中点,点P 是以点A为圆心、以AE长为半径的圆弧上的动点, ∴A P= ,∵∠PAQ=∠BAP,∴△APQ∽△ABP,∴ PQ= 当Q,P,C三点共线.时 的值最小.在 Rt△ACQ中,AC=4,AQ=1,∴ 的最小值为
例5 +1
【针对训练】
9. B 【解析】如解图,将AC 绕点 A 顺时针旋转90°得到AG,连接CG,EG,∴∠GAC=90°,∵等边△ABC的边长为1,AF为BC边上的高,∴CB=AC=AG=1,∠BAC=∠BCD=60°,AF 平分∠BAC,∴ ∠CAF=30°,∠GAE=∠GAC-∠CAF=60°,∴ ∠BCD=∠GAE,在△BCD 和△GAE 中,
CE=GE+CE≥CG,∴当点 C,E,G在同一直线上时,GE+CE 的值最小,在 Rt△ACG 中, BD+CE 的最小值为
模型九 几何图形最值模型
类型 ① 将军饮马
模型 图示 作法 原理
点 A,B 在直线l异侧 连接AB 交直线 l 于点 P,点 P 即为所求作的点 两点之间线段最短
点 A,B 在直线l同侧 作点A关于直线l的对称点; 连接 交直线l于点P,点P即为所求作的点
例1 如图,正方形ABCD的边长为8,点 M 在 CD上,且 ,N是AC上的一个动点,则DN+MN的最小值为 ( )
A. 6 B. 8 C. 10
针对训练
1. 如图,已知. 点P 为. 内部一点,点M 为射线OA、点N 为射线OB上的两个动点,当 的周长最小时,则
2.如图,等边三角形ABC的边长为4,E为BC边上的动点,F为AE的中点,则BF+CF的最小值为 ( )
C. 5
类型 造桥选址
问题描述 图示 作法 原理
已知直线 在直线m,n上分别求点M,N,使 直线 m,且. BN的值最小 将点 A 向下平移MN 的长度单位得点 连接 交直线n于点 N,过点N 作 直线 m于点M,连接AM,点M,N即为所求 两点之间线段最短
在直线l上求两点P,P'(点 P 在点. 左侧),并使 的值最小 将点 A 向右平移 的长度单位得 点 ,作点 B 关于 直线 l 的对称点 连接 与直线l的交点 即为点 将点 向左平移. 的 长度单位即为点P 两点之间线段最短
例2 人、、上P86问题2改编]已知A地和B地在一条河的两岸(河岸平行),现要在河上建一座垂直于河岸的桥 MN,请在图中找到合适的建桥位置,使从A 地到 B 地的路径. MN+NB 最短.
【自主作图】
【点拨】利用两点之间线段最短进行求解,要使 最短,即为求解. 的最小值
①将点A 沿着垂直于河岸b的方向平移到点. 使得
②连接 交河岸b于点N,
③过点N作 ,交河岸a于点M,连接AM,可以发现此时 即
针对训练
3. [2023鞍山月考]如图,在平面直角坐标系中,已知A(3,6),B(-2,2),在x轴上取两点C,D(点C在点D 左侧),且始终保持( ,线段CD在x轴上平移,当. 的值最小时,点C 的坐标为 .
如图,在矩形ABCD中, G是AD的中点,线段 EF 在边 AB 上左右滑动,连接GE,CF,若 则 的最小值为 .
类型3 胡不归
问题描述 已知点P 是线段BC 上一动点,点A 是直线BC 外一定点,连接PA,求, k·PB的最小值(
图示
作法 在线段BC异于点A的一侧作 使 过点P作 于点D,则 ,则求PA 的最小值即为求. 的最小值; 过点A作 于点 交BC于点 点 即为 取最小值时点P的位置
原理 垂线段最短
例3 [2023 锦州14题3分]如图,在 Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,按下列步骤作图:①在AC和AB上分别截取AD,AE,使AD=AE.②分别以点 D 和点 E为圆心,以大于 的长为半径作弧,两弧在∠BAC内交于点M.③作射线AM交BC于点F.若点P是线段AF上的一个动点,连接CP,则 的最小值是 .
【点拨】本题是一道典型的利用胡不归模型解决线段和最值的问题,胡不归模型的重点就在于能否把a+kb转化成为a+c,根据题目中所给的条件,判断AF 为角平分线,利用胡不归模型构建直角三角形,转化两条线段和为一条线段,利用三角函数求出线段长度.
针对训练
5. 如图,在△ABC中,∠A=15°,AB=10,P为AC边上的一个动点(不与A,C重合),连接BP,则 的最小值是 ( )
D. 8
如图,在矩形ABCD中, 点P为BC边上一点,则 的最小值是 .
类型4 阿氏圆
问题描述 已知点 P为⊙O上一动点,点A,B为⊙O外两定点,连接PB,PA,求PA+k·PB的最小值(0
作法 在线段OB上截取OC=k·r=k·OP,则可得 k,∠POC = ∠BOP,故 △OBP ∽△OPC),∴PC=k·PB,则求PA+k·PB 的最小值即为求PA+PC的最小值;连接AC,交⊙O 于点 P',点 P'即为 PA+k·PB取最小值时点P的位置
原理 两点之间线段最短
例4 如图,在Rt△ABC中,∠C=90°,AC=9,BC=4,以点C 为圆心,3为半径作⊙C,分别交AC,BC于D,E两点,点P 是⊙C上一个动点,则 的最小值为 .
【点拨】利用相似三角形将 转化为 PQ.在AC上截取CQ=1,连接CP,PQ,BQ,证明△ACP∽△PCQ,可得 当 B、Q、P 三点共线时, 的值最小,求出 BQ即可.
针对训练
7. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D,E分别是边BC,AC上的两个动点,且DE=4,P是DE的中点,连接PA,PB,则 的最小值为 .
.如图,在△ABC中,∠A=90°,AB=AC=4,点E,F分别是边AB,AC的中点,点 P 是以A为圆心、以AE长为半径的圆弧上的动点,则 的最小值为 .
类型 费马点
问题描述 图示 思路 作法 原理
在 任 意 内确定一点P,使得PA 最小 将以 P 为顶点的三角形旋转 得到等边三角形,则三条共顶点(点P)线段转化为首尾相连的折线段 将 绕点B顺时针旋转 得到 连接 得到等边三角形. 则 当 PA, 和 在一条直线上时, 最小 两点之间线段最短
例5 如果点P 是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫 的费马点.已经证明:在三个内角均小于120°的△ABC 中,当∠APB=∠APC=∠BPC=120°时,点P 就是△ABC的费马点.若点 P 是腰长为 的等腰直角三角形DEF的费马点,则PD+PE+PF= .
【点拨】过点D作DM⊥EF 于点M,在△DEF 内部过E,F分别作∠ ,结合费马点的定义,求出 PE,PF,DP的长即可解决问题.
针对训练
9.如图,等边△ABC的边长为1,AF为BC边上的高,点D,E分别为AC,AF上的两个动点,且满足CD=AE,则BD+CE的最小值为 ( )
A. 1
10. 组合练 如图,D是等边三角形ABC 外一点,连接AD,BD,CD,已知. 则当线段AD的长度最小时.
(1)∠BDC= ;
(2)AD 的最小值是 .
模型九 几何图形最值模型
例1 C
【针对训练】
1.80° 【解析】如解图,作点P 关于OB 的对称点 E,连接EO,EM,∴EM=MP,∠MPO=∠OEM,∠EOM=∠MOP,作点 P 关于OA 的对称点 F,连接 NF,OF,∴ PN=FN,∠OPN=∠OFN,∠PON=∠NOF,∴PM+PN+MN=EM+NF+MN≥EF,∴当E,M,N,F四点共线时,△PMN周长最小,又∵ ∠EOF=∠EOM+∠MOP+∠PON+∠NOF,∠AOB=∠MOP+∠PON,∴∠EOF=2∠AOB,又∵∠AOB=50°,∴∠EOF=100°,∵在△EOF中,∠OEM+∠OFN+∠EOF=180°,∴ ∠OEM+∠OFN=180°-100°=80°,∵∠MPO=∠OEM,∠OPN=∠OFN,∴∠MPO+∠OPN=80°,即∠MPN=80°.
2. B 【解析】如解图,分别取AB,AC 的中点M,N,作直线MN、由三角形中位线定理知MN与AE的交点为AE的中点F,即点 F 是直线 MN上的一个动点,作点 B 关于 MN的对称点B',连接B'C,B'F,则B'F=BF,∴BF+CF=B'F+CF≥B'C,∴BF+CF的最小值为B'C的长,由题意知BC=4,则等边△ABC中,BC边上的高为2 ,∴B'B=2 在 Rt△B'CB 中, 2
例2 解:桥MN的位置如解图所示.
3.(-1,0) 【解析】如解图,把A(3,6)向左平移1个单位长度得A'(2,6),作点B关于x轴的对称点 B',连接B'A'交x轴于点C,在x轴上取点D(点C 在点 D 左侧),使CD=1,连接AD,此时AD+BC的值最小,∵B(-2,2),∴B'(-2,-2),设直线 B'A'的解析式为 y= kx+b,∴ 解得 直线 B'A'的解析式为y=2x+2,当y=0时,x=-1,∴C(-1,0).
4.3 【解析】解法1:如解图①,作点G关于AB的对称点G',在CD上截取CH=1,连接HG'交AB 于点 E,在EB上截取EF=1,则GE=G'E,此时GE+CF的值最小,∵ CH=EF=1,CH∥EF,∴四边形EFCH是平行四边形,∴EH=CF,∴ G'H=EG'+EH=EG+CF,∵AB=4,BC=AD=2,G为边AD的中点,∴DG'=AD+AG'=2+1=3,DH=4-1=3,在Rt△G'DH中,由勾股定理得 即GE+CF的最小值为3
解法2:如解图①, 设AE=x,则.BF=AB-EF-AE=4-x-1=3-x,E由勾股定理得 EG+CF= 如解图②,在矩形 MNKR 中,MR=3,KR=2,KQ=1,P为NK上一动点,设 PK=y,则 由解图②可知,当M,P,Q 三点共线时,MP+PQ 最小,最小值是3 ,即EG+CF 的最小值是3
例3 2 5. B
6. 【解析】如解图,在矩形外作∠BCM=30°,过点 P作PE⊥CM,则 过点A作AF⊥CM于点 F,交 BC于点 P', 的最小值为 AF 的长,∵∠AP'B=∠CP'F=90°-∠BCM=60°,
∠B=90°,在 Rt△ABP'中, 在Rt△CFP'中,
例4
【针对训练】
【解析】如解图,在CB 上取一点 F,使得 连接PF,AF,PC.∵∠DCE=90°,DE=4,P 为DE的中点, =∠BCP,∴△PCF∽△BCP,∴PF=CF= ,∴PF = ∴当F,P,A三点共线时 的值最小,在 Rt△ACF 中, 的最小值为
8. 【解析】如解图,在AB上截取AQ=1,连接AP,PQ,CQ,∵点E,F分别是边AB,AC 的中点,点P 是以点A为圆心、以AE长为半径的圆弧上的动点, ∴A P= ,∵∠PAQ=∠BAP,∴△APQ∽△ABP,∴ PQ= 当Q,P,C三点共线.时 的值最小.在 Rt△ACQ中,AC=4,AQ=1,∴ 的最小值为
例5 +1
【针对训练】
9. B 【解析】如解图,将AC 绕点 A 顺时针旋转90°得到AG,连接CG,EG,∴∠GAC=90°,∵等边△ABC的边长为1,AF为BC边上的高,∴CB=AC=AG=1,∠BAC=∠BCD=60°,AF 平分∠BAC,∴ ∠CAF=30°,∠GAE=∠GAC-∠CAF=60°,∴ ∠BCD=∠GAE,在△BCD 和△GAE 中,
CE=GE+CE≥CG,∴当点 C,E,G在同一直线上时,GE+CE 的值最小,在 Rt△ACG 中, BD+CE 的最小值为
同课章节目录
