2025年中考数学培优思维训练二 转化思想(含解析)
文档属性
| 名称 | 2025年中考数学培优思维训练二 转化思想(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 298.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 00:00:00 | ||
图片预览


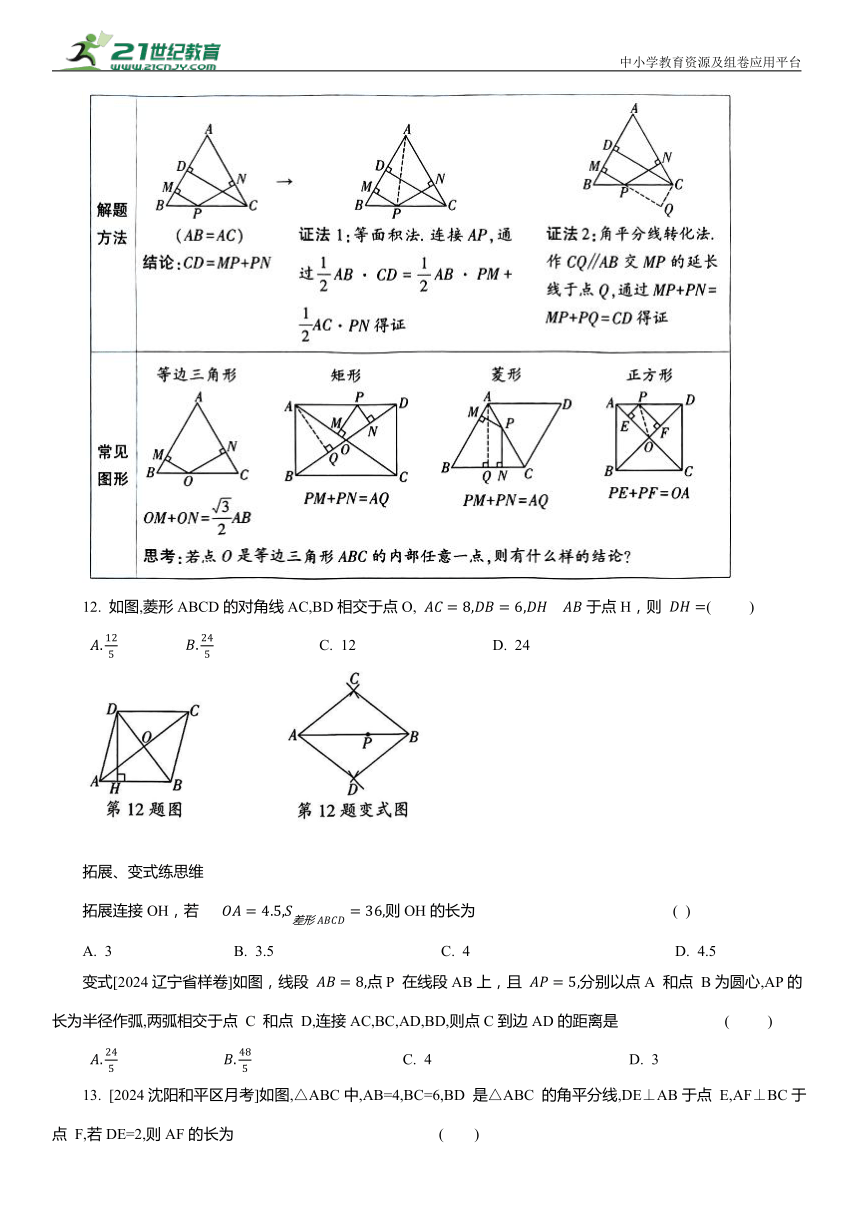
文档简介
思维训练二 转化思想
类型1 整体代入法
1. [2024锦州二模]若2a+3b=4,则整式-2a-3b+7的值是 ( )
A. - 3 B. 3 C. 5 D. 11
2. 多解法若关于x、y的二元一次方程组 的解满足 ,则m的值为 ( )
A. - 1 B. - 4 C. 1 D. - 2
3. 已知 则 的值等于 .
类型 消元法、换元法
4.用代入消元法解方程组 将①代入②可得 ( )
A. 5x-4x-2=7 B. 5x-2x-1=7 C. 5x-4x+1=7 D. 5x-4x+2=7
5.用加减消元法解方程组 下列运算能消去y的是 ( )
A. ①×2-② B. ①×3-②×2 C. ①×2+② D. ①×3+②×2
拓展消去未知数y后,能得到的一元一次方程是 ( )
A. x=6 B. 5x=3 C. 7x=9 D. 5x=6
6.关于x的方程( 则 的值是 .
类型 配方法
7.对于任意实数x,多项式 的值是一个 ( )
A.正数 B.负数
C.非负数 D.无法确定的数
8.【阅读理解】
例如 像这样先添加一个适当项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变的方法称之为配方法,配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值、最小值等等.
【解决问题】
请阅读以上材料,解决下列问题.
(1)请用适当的数字填空:
(2)已知a是任意实数,若 通过计算判断M,N的大小;
(3)[2023 沈阳15题改编]如图,用一段长为20米的篱笆围成一个长方形菜园,菜园的一面靠墙,墙长为12米.设与墙壁垂直的一边长为x米.当x取何值时,菜园面积最大,最大面积是多少平方米
类型 等量代换法
9. 如图,点C,D在线段AB上,若 则 ( )
D. CD=BC
拓展若 则
10.如图,在正方形网格中,每个小正方形的边长都是1,⊙O 是 的外接圆,点A,B,0在网格线的交点上,则( 的值是 ( )
11. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,PD⊥AC于点D,连接OP.求证:PD 是⊙O 的切线.
类型 ⑤ 等面积法
12. 如图,菱形ABCD的对角线AC,BD相交于点O, 于点H,则 ( )
C. 12 D. 24
拓展、变式练思维
拓展连接OH,若 则OH的长为 ( )
A. 3 B. 3.5 C. 4 D. 4.5
变式[2024辽宁省样卷]如图,线段 点P 在线段AB上,且 分别以点A 和点 B为圆心,AP的长为半径作弧,两弧相交于点 C 和点 D,连接AC,BC,AD,BD,则点C到边AD的距离是 ( )
C. 4 D. 3
13. [2024沈阳和平区月考]如图,△ABC中,AB=4,BC=6,BD 是△ABC 的角平分线,DE⊥AB于点 E,AF⊥BC于点 F,若DE=2,则AF的长为 ( )
C. 6
14.多解法如图,在Rt△ABC中,BM=3,AM是斜边 BC上的高,以AM为边作正方形AMEF.若 则AC= ( )
A. 11 C. 12 D. 16
类型 6 割补法
15.如图是利用割补法求图形面积的示意图,下列公式中与之相对应的是 ( )
16.如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(4a,a)是反比例函数 的图象与正方形的一个交点,若图中阴影部分的面积等于16,则k的值为 ( )
A. 16 B. 1 C. 4 D. - 16
17. 多解法如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,连接CE,BE,若AB=6cm,则图中阴影部分的面积为 cm .
18. 如图,在等腰三角形ABC中,∠B=90°,D为AC边的中点,过点 D 作DE⊥DF,交AB于点E,交 BC于点 F,若 则△ABC的面积为 ( )
A. 12 B. 14 C. 16 D. 18
思维训练二 转化思想
1. B
2. A 【解析】解法1: ①+②得2x+2y=2m+4.∵x+y=1,∴2x+2y=2=2m+4,∴m=-1;
解法2 ③-④得2y=2,∴y=1,∴x=0,∴x-y=2m+1=-1,∴m=-1.
3. 1 4. A 5. C 拓展C 6. 1 7. B
8. 解:(1)9;3;
∴M>N;
(3)由题意可得与墙壁平行的一边长为(20-2x)米,则0<20-2x≤12,
解得4≤x<10,
设菜园面积为y平方米,则
∴当x=5时,菜园面积最大,最大面积是50平方米.
9. B 拓展7 10. A
11. 证明略.
12. B 拓展 C 变式 A 13. A
14. B 【解析】解法 1:∵ S正方形AMEF = 16,∴ AM=4,在Rt△ABM中, ,在 Rt△ABC中,由勾股定理得 即 在 Rt△AMC中,同理可得AC =16+CM ,∴25+16+CM =(3+CM) ,解得
解法2:由解法1得 在 Rt△ABC中,AC
解法3:易证△ABM∽△CAM,由 易得 解法4:易证△ABM∽△CBA,由 易得
15. A 16. C
中小学教育资源及组卷应用平台
17. 3π 【解析】解法1:在正方形ABCD 中,∠DCB=90°,DC=AB=6cm.扇形 BAC 与扇形 CBD的弧交于点 E,∴△BCE是等边三角形,∴ ∠ECB =60°,∴ ∠DCE=∠DCB-∠ECB=30°.根据图形的割补,
解法2:同解法 1 可知,△BCE 是等边三角形,∴∠EBC=60°,观察题图发现,
D
类型1 整体代入法
1. [2024锦州二模]若2a+3b=4,则整式-2a-3b+7的值是 ( )
A. - 3 B. 3 C. 5 D. 11
2. 多解法若关于x、y的二元一次方程组 的解满足 ,则m的值为 ( )
A. - 1 B. - 4 C. 1 D. - 2
3. 已知 则 的值等于 .
类型 消元法、换元法
4.用代入消元法解方程组 将①代入②可得 ( )
A. 5x-4x-2=7 B. 5x-2x-1=7 C. 5x-4x+1=7 D. 5x-4x+2=7
5.用加减消元法解方程组 下列运算能消去y的是 ( )
A. ①×2-② B. ①×3-②×2 C. ①×2+② D. ①×3+②×2
拓展消去未知数y后,能得到的一元一次方程是 ( )
A. x=6 B. 5x=3 C. 7x=9 D. 5x=6
6.关于x的方程( 则 的值是 .
类型 配方法
7.对于任意实数x,多项式 的值是一个 ( )
A.正数 B.负数
C.非负数 D.无法确定的数
8.【阅读理解】
例如 像这样先添加一个适当项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变的方法称之为配方法,配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值、最小值等等.
【解决问题】
请阅读以上材料,解决下列问题.
(1)请用适当的数字填空:
(2)已知a是任意实数,若 通过计算判断M,N的大小;
(3)[2023 沈阳15题改编]如图,用一段长为20米的篱笆围成一个长方形菜园,菜园的一面靠墙,墙长为12米.设与墙壁垂直的一边长为x米.当x取何值时,菜园面积最大,最大面积是多少平方米
类型 等量代换法
9. 如图,点C,D在线段AB上,若 则 ( )
D. CD=BC
拓展若 则
10.如图,在正方形网格中,每个小正方形的边长都是1,⊙O 是 的外接圆,点A,B,0在网格线的交点上,则( 的值是 ( )
11. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,PD⊥AC于点D,连接OP.求证:PD 是⊙O 的切线.
类型 ⑤ 等面积法
12. 如图,菱形ABCD的对角线AC,BD相交于点O, 于点H,则 ( )
C. 12 D. 24
拓展、变式练思维
拓展连接OH,若 则OH的长为 ( )
A. 3 B. 3.5 C. 4 D. 4.5
变式[2024辽宁省样卷]如图,线段 点P 在线段AB上,且 分别以点A 和点 B为圆心,AP的长为半径作弧,两弧相交于点 C 和点 D,连接AC,BC,AD,BD,则点C到边AD的距离是 ( )
C. 4 D. 3
13. [2024沈阳和平区月考]如图,△ABC中,AB=4,BC=6,BD 是△ABC 的角平分线,DE⊥AB于点 E,AF⊥BC于点 F,若DE=2,则AF的长为 ( )
C. 6
14.多解法如图,在Rt△ABC中,BM=3,AM是斜边 BC上的高,以AM为边作正方形AMEF.若 则AC= ( )
A. 11 C. 12 D. 16
类型 6 割补法
15.如图是利用割补法求图形面积的示意图,下列公式中与之相对应的是 ( )
16.如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(4a,a)是反比例函数 的图象与正方形的一个交点,若图中阴影部分的面积等于16,则k的值为 ( )
A. 16 B. 1 C. 4 D. - 16
17. 多解法如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,连接CE,BE,若AB=6cm,则图中阴影部分的面积为 cm .
18. 如图,在等腰三角形ABC中,∠B=90°,D为AC边的中点,过点 D 作DE⊥DF,交AB于点E,交 BC于点 F,若 则△ABC的面积为 ( )
A. 12 B. 14 C. 16 D. 18
思维训练二 转化思想
1. B
2. A 【解析】解法1: ①+②得2x+2y=2m+4.∵x+y=1,∴2x+2y=2=2m+4,∴m=-1;
解法2 ③-④得2y=2,∴y=1,∴x=0,∴x-y=2m+1=-1,∴m=-1.
3. 1 4. A 5. C 拓展C 6. 1 7. B
8. 解:(1)9;3;
∴M>N;
(3)由题意可得与墙壁平行的一边长为(20-2x)米,则0<20-2x≤12,
解得4≤x<10,
设菜园面积为y平方米,则
∴当x=5时,菜园面积最大,最大面积是50平方米.
9. B 拓展7 10. A
11. 证明略.
12. B 拓展 C 变式 A 13. A
14. B 【解析】解法 1:∵ S正方形AMEF = 16,∴ AM=4,在Rt△ABM中, ,在 Rt△ABC中,由勾股定理得 即 在 Rt△AMC中,同理可得AC =16+CM ,∴25+16+CM =(3+CM) ,解得
解法2:由解法1得 在 Rt△ABC中,AC
解法3:易证△ABM∽△CAM,由 易得 解法4:易证△ABM∽△CBA,由 易得
15. A 16. C
中小学教育资源及组卷应用平台
17. 3π 【解析】解法1:在正方形ABCD 中,∠DCB=90°,DC=AB=6cm.扇形 BAC 与扇形 CBD的弧交于点 E,∴△BCE是等边三角形,∴ ∠ECB =60°,∴ ∠DCE=∠DCB-∠ECB=30°.根据图形的割补,
解法2:同解法 1 可知,△BCE 是等边三角形,∴∠EBC=60°,观察题图发现,
D
同课章节目录
