2025年中考数学培优模型一 遇到中点咋思考(含解析)
文档属性
| 名称 | 2025年中考数学培优模型一 遇到中点咋思考(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 13:49:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
模型一 遇到中点咋思考
类型 ① 遇一边中点,想三角形中位线
已知 作法 结论
在 中,点 D 是 BC 的中点 取AB的中点E(或取AC的中点 F),连接DE(或DF) (或
例1 [2023鞍山7题3分]如图,AC,BC为⊙O的两条弦,D,G分别为AC,BC的中点,⊙O的半径为2.若∠C=45°,则DG的长为 ( )
A. 2
【点拨】看到D,G分别为AC,BC的中点,连接AB,根据中位线定理,可得
类型 遇直角三角形斜边中点,想斜边中线
已知 作法 结论
在 △ABC 中, 点D是斜边 AB 的中点 即
例2 如图,在Rt△ABC中,∠ ,以点 C 为圆心,CA 长为半径作⊙O 与AB 交于点 D,若点 D 恰好为线段AB 的中点,则AB的长度为 ( )
B. 3
C. 6 D. 9
【点拨】∵点D为线段AB的中点,且. ∴由直角三角形的斜边中点可考虑斜边中线,可直接得出
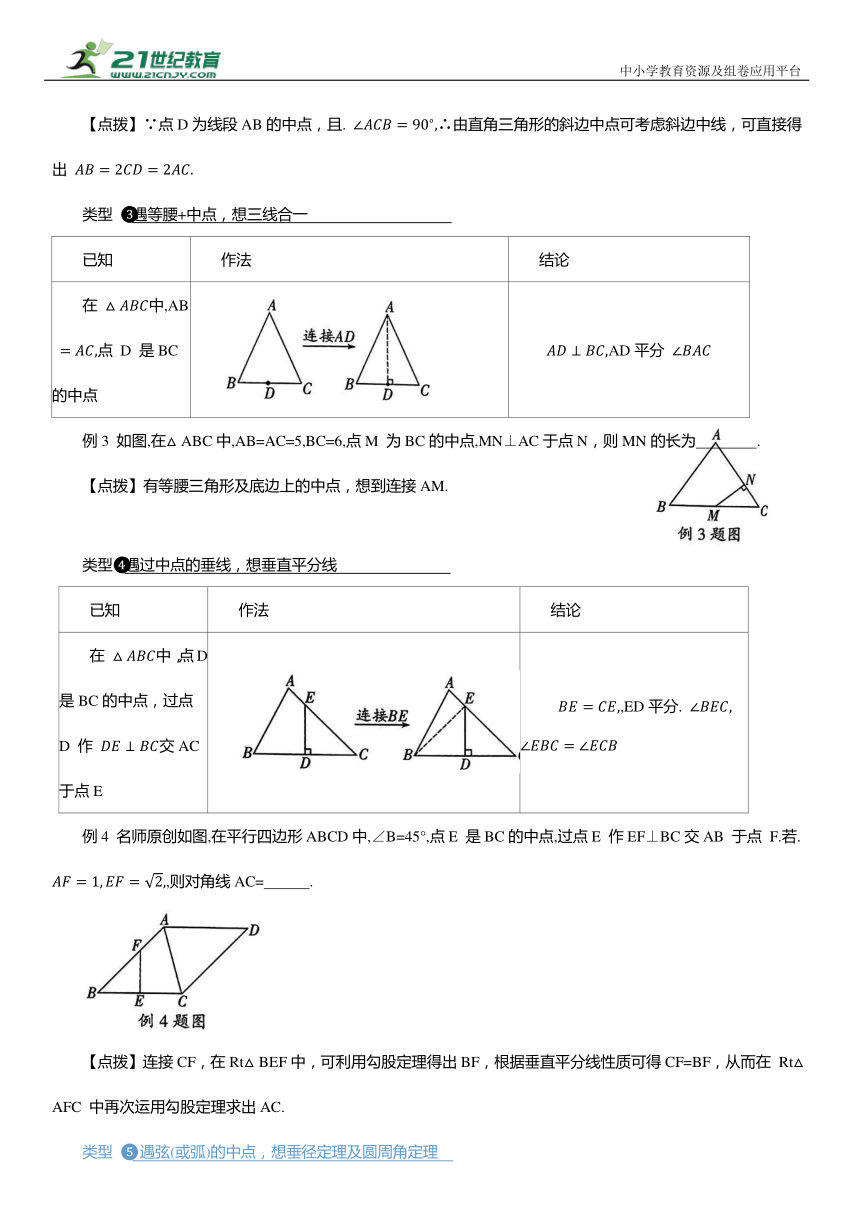
类型 遇等腰+中点,想三线合一
已知 作法 结论
在 中,AB 点 D 是BC的中点 AD平分
例3 如图,在△ABC中,AB=AC=5,BC=6,点M 为BC的中点,MN⊥AC于点N,则MN的长为 .
【点拨】有等腰三角形及底边上的中点,想到连接AM.
类型 遇过中点的垂线,想垂直平分线
已知 作法 结论
在 中,点D是BC的中点,过点 D 作 交AC于点E ,ED平分.
例4 名师原创如图,在平行四边形ABCD中,∠B=45°,点E 是BC的中点,过点E 作EF⊥BC交AB 于点 F.若. ,则对角线AC= .
【点拨】连接CF,在Rt△BEF中,可利用勾股定理得出BF,根据垂直平分线性质可得CF=BF,从而在 Rt△AFC 中再次运用勾股定理求出AC.
类型 遇弦(或弧)的中点,想垂径定理及圆周角定理
已知 作法 结论
在⊙O中, 点E是弦AB的中点
在⊙O中, 点C是 的中点 DC平分
例5 [2024沈阳皇姑区月考]如图,四边形ABCD 内接于⊙O,AB 是⊙O的直径,D是 的中点.若 ,则∠A 的大小为 ( )
A. 50°
B. 60°
C. 70°
D. 80°
【点拨】看到 D是. 的中点,结合角度,可想到圆周角定理,连接BD,可得 结合三角形内角和性质即可求出
类型 6 遇中点或中线,想倍长中线构造全等
已知 作法 结论
在 中,AD为BC边上的中线 延长AD 至点E,使得 若连接BE, 则 若连接CE, 则
例6 如图,在△ABC中,AD是BC边上的中线,E是AD 上一点,且. 延长BE交AC于点 F,若EF=2,则AF的长为 .
针对训练
1. 如图,在⊙O中,弦AB=12,半径OC⊥AB于点P,且P为OC的中点,则AC的长是( )
B. 6C. 8
2. 多解法如图,在Rt△ABC 中,∠B=90°,AB=2,点 D 是 AC 的中点,点 E 在边 BC上,且∠DEC=45°,则 DE的长为 .
如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线 DE 交 BC的延长线于点E,则CE 的长为 .
4. [2024 沈阳皇姑区期末]如图,在正方形ABCD 和正方形 CEFG中,点D在CG上,BC=1,CE ,H是AF的中点,则CH的长是 .
5. [2024广州]如图,在 中,. ,D 为边 BC的中点,点 E,F 分别在边AB,AC上, 则四边形 AEDF的面积为 ( )
A. 18 C. 9
6. [2024 沈阳和平区月考]如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点 N是 BC边上一点,点M为AB边上的动点,点D,E分别为CN,MN的中点,则DE的最小值是 ( )
A. 2 C. 3
7.多解法如图,正方形ABCD 和正方形EFCG的边长分别为3和1,连接AE,点F,G分别在边 BC,CD上,P为AE的中点,连接PG,则PG的长为 .
8. 如图,点E是BC的中点,点A在DE上,∠BAE=∠CDE.求证:AB=CD.
模型一 遇到中点咋思考
例1 D 例2 C 例3 例4 例5 C
例6 2
【针对训练】
1. D 【解析】如解图,连接OA,设⊙O 的半径为r,∵ P为OC的中点,∴OP=CP= r,∵OP⊥AB,∴AP=BP= 在 Rt△OAP中, 即 r ,解得 (负值已舍去),∴PC=2 ,在Rt△APC中,
2. 【解析】解法1:如解图①,过点 D 作 DF∥AB 交BC于点 F,∵点D是AC的中点,∠B=90°,∴∠DFE=90°,DF为△ABC的中位线,∴ ∵在Rt△DFE中,∠DEC=45°,∴DE= DF=
解法2:如解图②,过点A 作 DE的平行线交 CB 延长线于点 F,∵ ∠DEC=45°,∴ ∠AFC =45°,∴ AF= 又∵点 D 是 AC 的中点,∴ DE 为△AFC的中位线,∴
3. 4.
5. C 【解析】如解图,连接AD,∵∠BAC=90°,AB=AC=6,D为边 BC的中点,∴AD=BD=CD,∠BAD=∠C=45°, 在△ADE 和△CDF 中,(LEAOS∠C,∴ △ADE≌△ODF,∴S,△CDF,∴
6. B 【解析】如解图,连接CM,当CM⊥AB时,CM 的值最小(垂线段最短),此时DE有最小值,∵∠C=90°,AC= ∵点D,E分别为 CN,MN的中点,∴ ,即DE的最小值是
7. 【解析】解法1:如解图①,延长GE交AB 于点O,过点P作PH⊥OE 于点 H,则 PH∥AB,∵P 是AE 的中点,∴PH是△AOE的中位线,∴ ∵在 Rt△AOE中,∠OAE=45°,∴ △AOE 是等腰直角三角形,即OE=OA=2,同理,在△PHE中,HE=PH=1,∴HG=HE+EG=1+1=2.在 Rt△PHG中,
解法2:如解图②,延长GP 至点 Q,使得 PQ=PG,连接AQ,在△APQ 和△EPG中 △EPG(SAS),∴AQ=EG=1,∠QAP=∠GEP,∴AQ∥EG,即Q,A,D三点共线,∴QD=AQ+AD=4,又∵DG=DC-CG=2,∴在 Rt△QGD 中,
8. 证明:略.
模型一 遇到中点咋思考
类型 ① 遇一边中点,想三角形中位线
已知 作法 结论
在 中,点 D 是 BC 的中点 取AB的中点E(或取AC的中点 F),连接DE(或DF) (或
例1 [2023鞍山7题3分]如图,AC,BC为⊙O的两条弦,D,G分别为AC,BC的中点,⊙O的半径为2.若∠C=45°,则DG的长为 ( )
A. 2
【点拨】看到D,G分别为AC,BC的中点,连接AB,根据中位线定理,可得
类型 遇直角三角形斜边中点,想斜边中线
已知 作法 结论
在 △ABC 中, 点D是斜边 AB 的中点 即
例2 如图,在Rt△ABC中,∠ ,以点 C 为圆心,CA 长为半径作⊙O 与AB 交于点 D,若点 D 恰好为线段AB 的中点,则AB的长度为 ( )
B. 3
C. 6 D. 9
【点拨】∵点D为线段AB的中点,且. ∴由直角三角形的斜边中点可考虑斜边中线,可直接得出
类型 遇等腰+中点,想三线合一
已知 作法 结论
在 中,AB 点 D 是BC的中点 AD平分
例3 如图,在△ABC中,AB=AC=5,BC=6,点M 为BC的中点,MN⊥AC于点N,则MN的长为 .
【点拨】有等腰三角形及底边上的中点,想到连接AM.
类型 遇过中点的垂线,想垂直平分线
已知 作法 结论
在 中,点D是BC的中点,过点 D 作 交AC于点E ,ED平分.
例4 名师原创如图,在平行四边形ABCD中,∠B=45°,点E 是BC的中点,过点E 作EF⊥BC交AB 于点 F.若. ,则对角线AC= .
【点拨】连接CF,在Rt△BEF中,可利用勾股定理得出BF,根据垂直平分线性质可得CF=BF,从而在 Rt△AFC 中再次运用勾股定理求出AC.
类型 遇弦(或弧)的中点,想垂径定理及圆周角定理
已知 作法 结论
在⊙O中, 点E是弦AB的中点
在⊙O中, 点C是 的中点 DC平分
例5 [2024沈阳皇姑区月考]如图,四边形ABCD 内接于⊙O,AB 是⊙O的直径,D是 的中点.若 ,则∠A 的大小为 ( )
A. 50°
B. 60°
C. 70°
D. 80°
【点拨】看到 D是. 的中点,结合角度,可想到圆周角定理,连接BD,可得 结合三角形内角和性质即可求出
类型 6 遇中点或中线,想倍长中线构造全等
已知 作法 结论
在 中,AD为BC边上的中线 延长AD 至点E,使得 若连接BE, 则 若连接CE, 则
例6 如图,在△ABC中,AD是BC边上的中线,E是AD 上一点,且. 延长BE交AC于点 F,若EF=2,则AF的长为 .
针对训练
1. 如图,在⊙O中,弦AB=12,半径OC⊥AB于点P,且P为OC的中点,则AC的长是( )
B. 6C. 8
2. 多解法如图,在Rt△ABC 中,∠B=90°,AB=2,点 D 是 AC 的中点,点 E 在边 BC上,且∠DEC=45°,则 DE的长为 .
如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线 DE 交 BC的延长线于点E,则CE 的长为 .
4. [2024 沈阳皇姑区期末]如图,在正方形ABCD 和正方形 CEFG中,点D在CG上,BC=1,CE ,H是AF的中点,则CH的长是 .
5. [2024广州]如图,在 中,. ,D 为边 BC的中点,点 E,F 分别在边AB,AC上, 则四边形 AEDF的面积为 ( )
A. 18 C. 9
6. [2024 沈阳和平区月考]如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点 N是 BC边上一点,点M为AB边上的动点,点D,E分别为CN,MN的中点,则DE的最小值是 ( )
A. 2 C. 3
7.多解法如图,正方形ABCD 和正方形EFCG的边长分别为3和1,连接AE,点F,G分别在边 BC,CD上,P为AE的中点,连接PG,则PG的长为 .
8. 如图,点E是BC的中点,点A在DE上,∠BAE=∠CDE.求证:AB=CD.
模型一 遇到中点咋思考
例1 D 例2 C 例3 例4 例5 C
例6 2
【针对训练】
1. D 【解析】如解图,连接OA,设⊙O 的半径为r,∵ P为OC的中点,∴OP=CP= r,∵OP⊥AB,∴AP=BP= 在 Rt△OAP中, 即 r ,解得 (负值已舍去),∴PC=2 ,在Rt△APC中,
2. 【解析】解法1:如解图①,过点 D 作 DF∥AB 交BC于点 F,∵点D是AC的中点,∠B=90°,∴∠DFE=90°,DF为△ABC的中位线,∴ ∵在Rt△DFE中,∠DEC=45°,∴DE= DF=
解法2:如解图②,过点A 作 DE的平行线交 CB 延长线于点 F,∵ ∠DEC=45°,∴ ∠AFC =45°,∴ AF= 又∵点 D 是 AC 的中点,∴ DE 为△AFC的中位线,∴
3. 4.
5. C 【解析】如解图,连接AD,∵∠BAC=90°,AB=AC=6,D为边 BC的中点,∴AD=BD=CD,∠BAD=∠C=45°, 在△ADE 和△CDF 中,(LEAOS∠C,∴ △ADE≌△ODF,∴S,△CDF,∴
6. B 【解析】如解图,连接CM,当CM⊥AB时,CM 的值最小(垂线段最短),此时DE有最小值,∵∠C=90°,AC= ∵点D,E分别为 CN,MN的中点,∴ ,即DE的最小值是
7. 【解析】解法1:如解图①,延长GE交AB 于点O,过点P作PH⊥OE 于点 H,则 PH∥AB,∵P 是AE 的中点,∴PH是△AOE的中位线,∴ ∵在 Rt△AOE中,∠OAE=45°,∴ △AOE 是等腰直角三角形,即OE=OA=2,同理,在△PHE中,HE=PH=1,∴HG=HE+EG=1+1=2.在 Rt△PHG中,
解法2:如解图②,延长GP 至点 Q,使得 PQ=PG,连接AQ,在△APQ 和△EPG中 △EPG(SAS),∴AQ=EG=1,∠QAP=∠GEP,∴AQ∥EG,即Q,A,D三点共线,∴QD=AQ+AD=4,又∵DG=DC-CG=2,∴在 Rt△QGD 中,
8. 证明:略.
同课章节目录
