2025年中考数学培优模型二 遇到角平分线咋思考(含解析)
文档属性
| 名称 | 2025年中考数学培优模型二 遇到角平分线咋思考(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 320.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 13:48:03 | ||
图片预览



文档简介
模型二 遇到角平分线咋思考
类型 ① 作垂线构全等
已知 作法 结论
P 是∠MON 平分线上的一点, PA ⊥ OM 于点A 过点 P作PB⊥ON于点B AP=BP, Rt△AOP≌Rt△BOP
例1 如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,△ABC的面积为15,AB=6,DE=3,则AC 的长是 .
类型 2 截取(或延长)等线段构全等(截长补短)
已知 作法
AD 平分∠BAC,AB>AC 作法1:截长 在AB上截取AE=AC,连接DE 作法2:补短 延长AC至点F,使得AF=AB,连接DF
结论 △ADE≌△ADC △ADB≌△ADF
例2 多解法[2024 葫芦岛兴城市期末]如图,在△ABC中,AD 平分∠BAC,∠B=2∠C,若AC=5,AB=3,则BD的长度为 ( )
A. 1 B. 2 C. 3 D. 4
类型 巧用“三线合一”构等腰
已知 作法 结论
P是∠MON 平分线上的一点,若AP⊥OP 于点 P 延长AP交ON于点B △AOB是等腰三角形,△AOP≌△BOP
例3 多解法如图,在等腰直角三角形ABC 中, BD 平分 于点 E,若. 的面积为16,则BD的长为 ( )
A. 16 B. 8 C. 6 D. 4
类型 作边或角平分线的平行线构等腰
已知 作法 结论
P 是 平分线上的一点 作法1:作一边的平行线 过点P作. 交OM于点Q 是等腰三角形,
OP 是 的平分线,A 是OM 上一点 作法2:作角平分线的平行线 过点A作 交NO的延长线于点B 是等腰三角形,
例4 多解法如图,AD是△ABC的角平分线,交BC于点D,AB=5,AC=3,则
【点拨】解法1:AD平分∠BAC,考虑过点D 作AB的平行线,构造等腰三角形,再结合相似三角形的性质得线段比值.
解法2:过点C作AD的平行线与BA的延长线相交,构造等腰三角形,再结合相似三角形的性质得线段比值.
解法3:过点B 作AC的平行线与AD的延长线相交,构造等腰三角形,再结合相似三角形的性质得线段比值.
针对训练
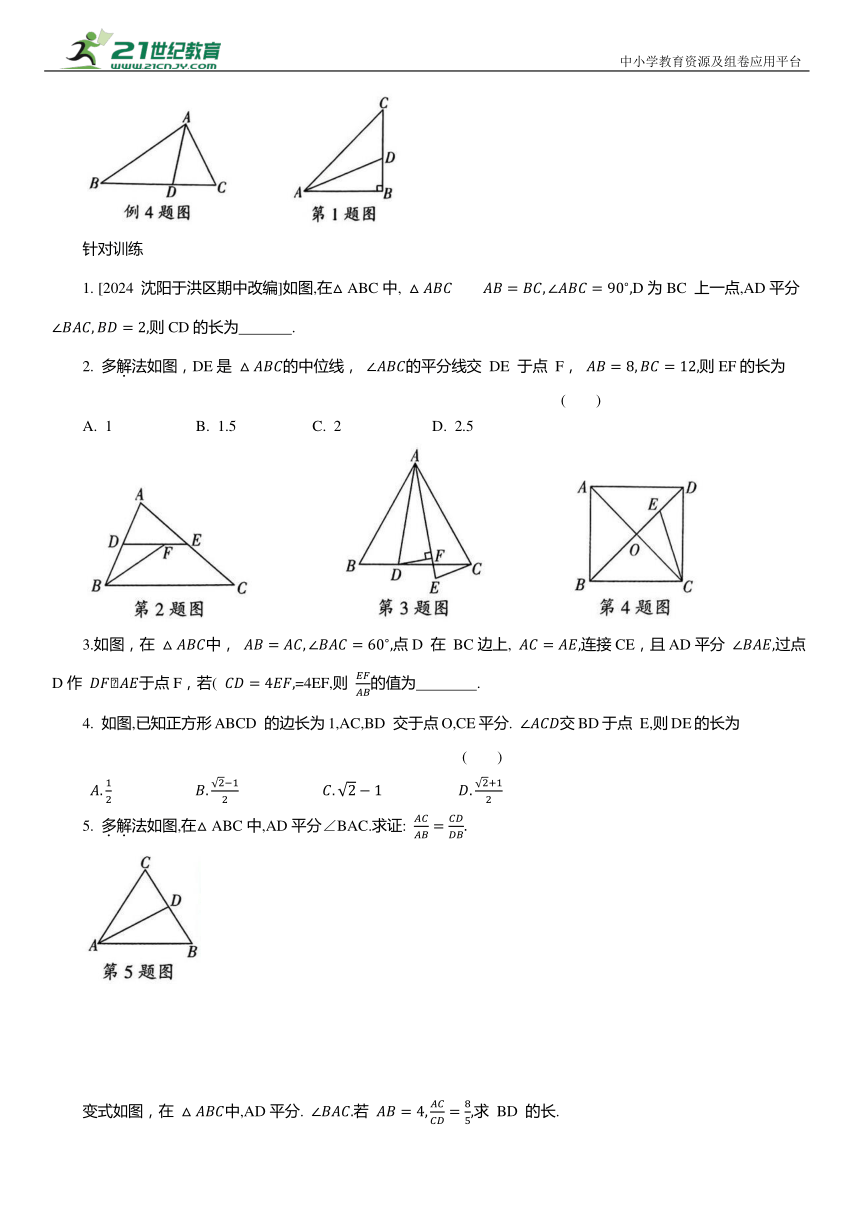
[2024 沈阳于洪区期中改编]如图,在△ABC中, D为BC 上一点,AD平分 则CD的长为 .
2. 多解法如图,DE是 的中位线, 的平分线交 DE 于点 F, 则EF的长为 ( )
A. 1 B. 1.5 C. 2 D. 2.5
3.如图,在 中, 点D 在 BC边上, 连接CE,且AD平分 过点D作 于点F,若( =4EF,则 的值为 .
4. 如图,已知正方形ABCD 的边长为1,AC,BD 交于点O,CE平分. 交BD于点 E,则DE的长为 ( )
5. 多解法如图,在△ABC中,AD平分∠BAC.求证:
变式如图,在 中,AD平分. 若 求 BD 的长.
6. 如图,在锐角. 中, BD 平分 CE平分 BD与 CE相交于点O,求证:
拓展练思维
拓展1 在上述条件下,可得
拓展2 连接AO并延长,交BC于点 Q,若 判断AQ 与BC 的位置关系为 ;
中小学教育资源及组卷应用平台
拓展3若 求 的值.
例1 4
例2 B 【解析】解法1(截长):如解图①,在AC 上截取AE=AB,连接DE,∵AD平分∠BAC,∴∠BAD=∠DAC,在△ABD 和△AED 中 ∴∠B=∠AED,BD=DE,∵∠B=2∠C,∴∠AED=2∠C,∵∠AED=∠C+∠CDE,∴∠CDE=∠C,∴ DE=CE=BD,∵AC=5,AB=AE=3,∴BD=CE=AC-AE=2.
解法2(补短):如解图②,延长AB至点 F,使AF=AC,连接DF,同理可证△AFD≌△ACD,得∠F=∠C,推出∠F=∠BDF,则BD=BF,则可推出BD=AC-AB=2.
例3 B 【解析】解法1:如解图①,延长CE交BA 的延长线于点 F,∵∠BAC=90°,∴∠CAF=90°,∵BD平分∠ABC,BE⊥CF,∴ ∠ABD = ∠CBD,∠BEC = 90°,∵ ∠BDA =∠CDE,∴∠ABD=∠ACF,∵AB=AC,∴△ABD≌△ACF,∴BD=CF,∵∠ABE=∠CBE,BE⊥CF,∴CF=BD=2CE,设CE=x,则BD=2x,∵△BCD的面积为16,∴ BD·CE 解得x=4(负值已舍去),∴BD=8.
解法2:如解图②,过点D 作DH⊥BC于点H,设AD=a,易得DH=a,DC= a,∴AC=AD+CD=(1+ )a,则BC= 由 =16,求得a =32-16 ,∵HC=DH=a,∴BH=BC-HC= 在Rt△BDH中,根据勾股定理求得BD=8.
例4 【解析】解法1:如解图①,过点 D 作DE∥AB交AC于点 E,∴∠BAD=∠ADE ,∵AD 是△ABC 的角平分线,∴∠BAD=∠CAD,∴∠ADE=∠CAD,∴DE=AE,设DE=AE=x,则EC=3-x,∵DE∥AB,∴△CDE∽△CBA,∴ECCA 解得 ,又∵
解法2:如解图②,过点 C 作 CF∥AD 交 BA 的延长线于点 F,∴ ∠F=∠BAD,∠DAC =∠ACF,∵ AD 是△ABC的角平分线,∴ ∠BAD =∠CAD,∴ ∠ACF=∠F,∴AF=AC=3,∵CF∥AD,∴BD=ABF=
解法3:如解图③,过点 B作BG∥AC 交AD 的延长线于点G,∴∠G=∠CAD,△BGD∽△CAD,∴BCA=BD,∵AD 是△ABC 的角平分线,∴ ∠BAD =∠DAC,∴∠BAD=∠G,∴AB=BG,∴BD=AC=AB=
【针对训练】
1. 2
2. C 【解析】解法1:∵DE 是△ABC的中位线,AB=8,BC=12,∴BD= AB=4,DE∥BC,DE= BC=6,∴∠DFB=∠CBF,∵ BF 是∠ABC 的平分线,∴ ∠DBF =∠CBF,∴∠DFB=∠DBF,∴DF=BD=4,∴EF=DE-DF=6-4=2.
解法2:如解图,连接AF并延长交BC于点H,∵DE是△ABC的中位线,∴D H,又∵BF 平分∠ABH,∴ BH=AB=8,∵ AD=DB,AF=FH,∴DF是△ABH的中位线,∴ ∴EF=DE-DF=2.
3.
4. C
5. 证明:解法1:过点 B 作BE∥AC交AD的延长线于点 E,如解图①,
∴∠C=∠DBE,
∵∠ADC=∠BDE,
∴△CAD∽△BED,
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∵AC∥BE,
∴∠CAD=∠E,
∴∠BAE=∠E,
∴AB=BE,
解法2:过点 D分别作DH⊥AB 于点 H,DF⊥AC 于点F,如解图②,设BC边上的高为h,∵AD平分∠BAC,
变式解:
6.证明略.
拓展1120° 拓展2AQ⊥BC;
拓展3解:如解图,过点B 作 BG⊥CE垂足为G,BG交CE的延长线于点 G,过点C作CH⊥AB,垂足为H,则∠G=∠CHA=90°,
由题已得∠EOB=60°,
∴∠CAH=∠BOG=60°,
∴∠ACH=30°,
在△ACH和△OBG中
∴△ACH≌△OBG,
∴BG=CH,∠OBG=∠ACH=30°,
在△BEG和△CEH中,
∴△BEG≌△CEH,
∴EB=EC,∠EBC=∠ECH,即∠EBG+∠EBO=30°
设∠EBG=∠ECH=x,则有x+∠EBO=30°,
即∠EBC=60°-2x,
∵∠ECB=∠ACE=∠ECH+∠ACH=x+30°,
∴60°-2x=x+30°,∴x=10°,
∴∠EBC=60°-2x=40°,即∠ABC=40°.
类型 ① 作垂线构全等
已知 作法 结论
P 是∠MON 平分线上的一点, PA ⊥ OM 于点A 过点 P作PB⊥ON于点B AP=BP, Rt△AOP≌Rt△BOP
例1 如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,△ABC的面积为15,AB=6,DE=3,则AC 的长是 .
类型 2 截取(或延长)等线段构全等(截长补短)
已知 作法
AD 平分∠BAC,AB>AC 作法1:截长 在AB上截取AE=AC,连接DE 作法2:补短 延长AC至点F,使得AF=AB,连接DF
结论 △ADE≌△ADC △ADB≌△ADF
例2 多解法[2024 葫芦岛兴城市期末]如图,在△ABC中,AD 平分∠BAC,∠B=2∠C,若AC=5,AB=3,则BD的长度为 ( )
A. 1 B. 2 C. 3 D. 4
类型 巧用“三线合一”构等腰
已知 作法 结论
P是∠MON 平分线上的一点,若AP⊥OP 于点 P 延长AP交ON于点B △AOB是等腰三角形,△AOP≌△BOP
例3 多解法如图,在等腰直角三角形ABC 中, BD 平分 于点 E,若. 的面积为16,则BD的长为 ( )
A. 16 B. 8 C. 6 D. 4
类型 作边或角平分线的平行线构等腰
已知 作法 结论
P 是 平分线上的一点 作法1:作一边的平行线 过点P作. 交OM于点Q 是等腰三角形,
OP 是 的平分线,A 是OM 上一点 作法2:作角平分线的平行线 过点A作 交NO的延长线于点B 是等腰三角形,
例4 多解法如图,AD是△ABC的角平分线,交BC于点D,AB=5,AC=3,则
【点拨】解法1:AD平分∠BAC,考虑过点D 作AB的平行线,构造等腰三角形,再结合相似三角形的性质得线段比值.
解法2:过点C作AD的平行线与BA的延长线相交,构造等腰三角形,再结合相似三角形的性质得线段比值.
解法3:过点B 作AC的平行线与AD的延长线相交,构造等腰三角形,再结合相似三角形的性质得线段比值.
针对训练
[2024 沈阳于洪区期中改编]如图,在△ABC中, D为BC 上一点,AD平分 则CD的长为 .
2. 多解法如图,DE是 的中位线, 的平分线交 DE 于点 F, 则EF的长为 ( )
A. 1 B. 1.5 C. 2 D. 2.5
3.如图,在 中, 点D 在 BC边上, 连接CE,且AD平分 过点D作 于点F,若( =4EF,则 的值为 .
4. 如图,已知正方形ABCD 的边长为1,AC,BD 交于点O,CE平分. 交BD于点 E,则DE的长为 ( )
5. 多解法如图,在△ABC中,AD平分∠BAC.求证:
变式如图,在 中,AD平分. 若 求 BD 的长.
6. 如图,在锐角. 中, BD 平分 CE平分 BD与 CE相交于点O,求证:
拓展练思维
拓展1 在上述条件下,可得
拓展2 连接AO并延长,交BC于点 Q,若 判断AQ 与BC 的位置关系为 ;
中小学教育资源及组卷应用平台
拓展3若 求 的值.
例1 4
例2 B 【解析】解法1(截长):如解图①,在AC 上截取AE=AB,连接DE,∵AD平分∠BAC,∴∠BAD=∠DAC,在△ABD 和△AED 中 ∴∠B=∠AED,BD=DE,∵∠B=2∠C,∴∠AED=2∠C,∵∠AED=∠C+∠CDE,∴∠CDE=∠C,∴ DE=CE=BD,∵AC=5,AB=AE=3,∴BD=CE=AC-AE=2.
解法2(补短):如解图②,延长AB至点 F,使AF=AC,连接DF,同理可证△AFD≌△ACD,得∠F=∠C,推出∠F=∠BDF,则BD=BF,则可推出BD=AC-AB=2.
例3 B 【解析】解法1:如解图①,延长CE交BA 的延长线于点 F,∵∠BAC=90°,∴∠CAF=90°,∵BD平分∠ABC,BE⊥CF,∴ ∠ABD = ∠CBD,∠BEC = 90°,∵ ∠BDA =∠CDE,∴∠ABD=∠ACF,∵AB=AC,∴△ABD≌△ACF,∴BD=CF,∵∠ABE=∠CBE,BE⊥CF,∴CF=BD=2CE,设CE=x,则BD=2x,∵△BCD的面积为16,∴ BD·CE 解得x=4(负值已舍去),∴BD=8.
解法2:如解图②,过点D 作DH⊥BC于点H,设AD=a,易得DH=a,DC= a,∴AC=AD+CD=(1+ )a,则BC= 由 =16,求得a =32-16 ,∵HC=DH=a,∴BH=BC-HC= 在Rt△BDH中,根据勾股定理求得BD=8.
例4 【解析】解法1:如解图①,过点 D 作DE∥AB交AC于点 E,∴∠BAD=∠ADE ,∵AD 是△ABC 的角平分线,∴∠BAD=∠CAD,∴∠ADE=∠CAD,∴DE=AE,设DE=AE=x,则EC=3-x,∵DE∥AB,∴△CDE∽△CBA,∴ECCA 解得 ,又∵
解法2:如解图②,过点 C 作 CF∥AD 交 BA 的延长线于点 F,∴ ∠F=∠BAD,∠DAC =∠ACF,∵ AD 是△ABC的角平分线,∴ ∠BAD =∠CAD,∴ ∠ACF=∠F,∴AF=AC=3,∵CF∥AD,∴BD=ABF=
解法3:如解图③,过点 B作BG∥AC 交AD 的延长线于点G,∴∠G=∠CAD,△BGD∽△CAD,∴BCA=BD,∵AD 是△ABC 的角平分线,∴ ∠BAD =∠DAC,∴∠BAD=∠G,∴AB=BG,∴BD=AC=AB=
【针对训练】
1. 2
2. C 【解析】解法1:∵DE 是△ABC的中位线,AB=8,BC=12,∴BD= AB=4,DE∥BC,DE= BC=6,∴∠DFB=∠CBF,∵ BF 是∠ABC 的平分线,∴ ∠DBF =∠CBF,∴∠DFB=∠DBF,∴DF=BD=4,∴EF=DE-DF=6-4=2.
解法2:如解图,连接AF并延长交BC于点H,∵DE是△ABC的中位线,∴D H,又∵BF 平分∠ABH,∴ BH=AB=8,∵ AD=DB,AF=FH,∴DF是△ABH的中位线,∴ ∴EF=DE-DF=2.
3.
4. C
5. 证明:解法1:过点 B 作BE∥AC交AD的延长线于点 E,如解图①,
∴∠C=∠DBE,
∵∠ADC=∠BDE,
∴△CAD∽△BED,
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∵AC∥BE,
∴∠CAD=∠E,
∴∠BAE=∠E,
∴AB=BE,
解法2:过点 D分别作DH⊥AB 于点 H,DF⊥AC 于点F,如解图②,设BC边上的高为h,∵AD平分∠BAC,
变式解:
6.证明略.
拓展1120° 拓展2AQ⊥BC;
拓展3解:如解图,过点B 作 BG⊥CE垂足为G,BG交CE的延长线于点 G,过点C作CH⊥AB,垂足为H,则∠G=∠CHA=90°,
由题已得∠EOB=60°,
∴∠CAH=∠BOG=60°,
∴∠ACH=30°,
在△ACH和△OBG中
∴△ACH≌△OBG,
∴BG=CH,∠OBG=∠ACH=30°,
在△BEG和△CEH中,
∴△BEG≌△CEH,
∴EB=EC,∠EBC=∠ECH,即∠EBG+∠EBO=30°
设∠EBG=∠ECH=x,则有x+∠EBO=30°,
即∠EBC=60°-2x,
∵∠ECB=∠ACE=∠ECH+∠ACH=x+30°,
∴60°-2x=x+30°,∴x=10°,
∴∠EBC=60°-2x=40°,即∠ABC=40°.
同课章节目录
