2025年中考数学培优模型三 半角模型(含解析)
文档属性
| 名称 | 2025年中考数学培优模型三 半角模型(含解析) | 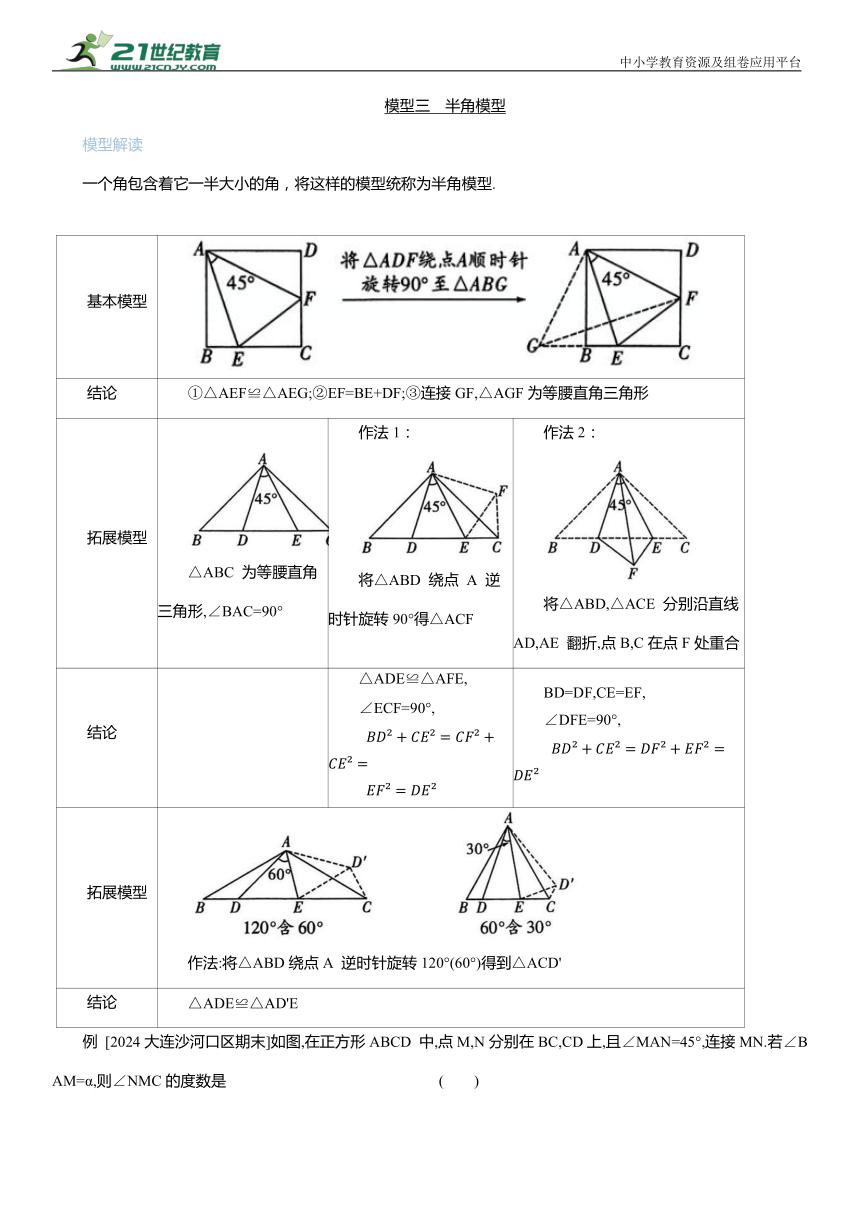 | |
| 格式 | docx | ||
| 文件大小 | 276.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 13:52:08 | ||
图片预览

文档简介
模型三 半角模型
模型解读
一个角包含着它一半大小的角,将这样的模型统称为半角模型.
基本模型
结论 ①△AEF≌△AEG;②EF=BE+DF;③连接GF,△AGF为等腰直角三角形
拓展模型 △ABC 为等腰直角三角形,∠BAC=90° 作法1: 将△ABD 绕点 A 逆时针旋转90°得△ACF 作法2: 将△ABD,△ACE 分别沿直线AD,AE 翻折,点B,C在点F处重合
结论 △ADE≌△AFE, ∠ECF=90°, BD=DF,CE=EF, ∠DFE=90°,
拓展模型 作法:将△ABD绕点A 逆时针旋转120°(60°)得到△ACD'
结论 △ADE≌△AD'E
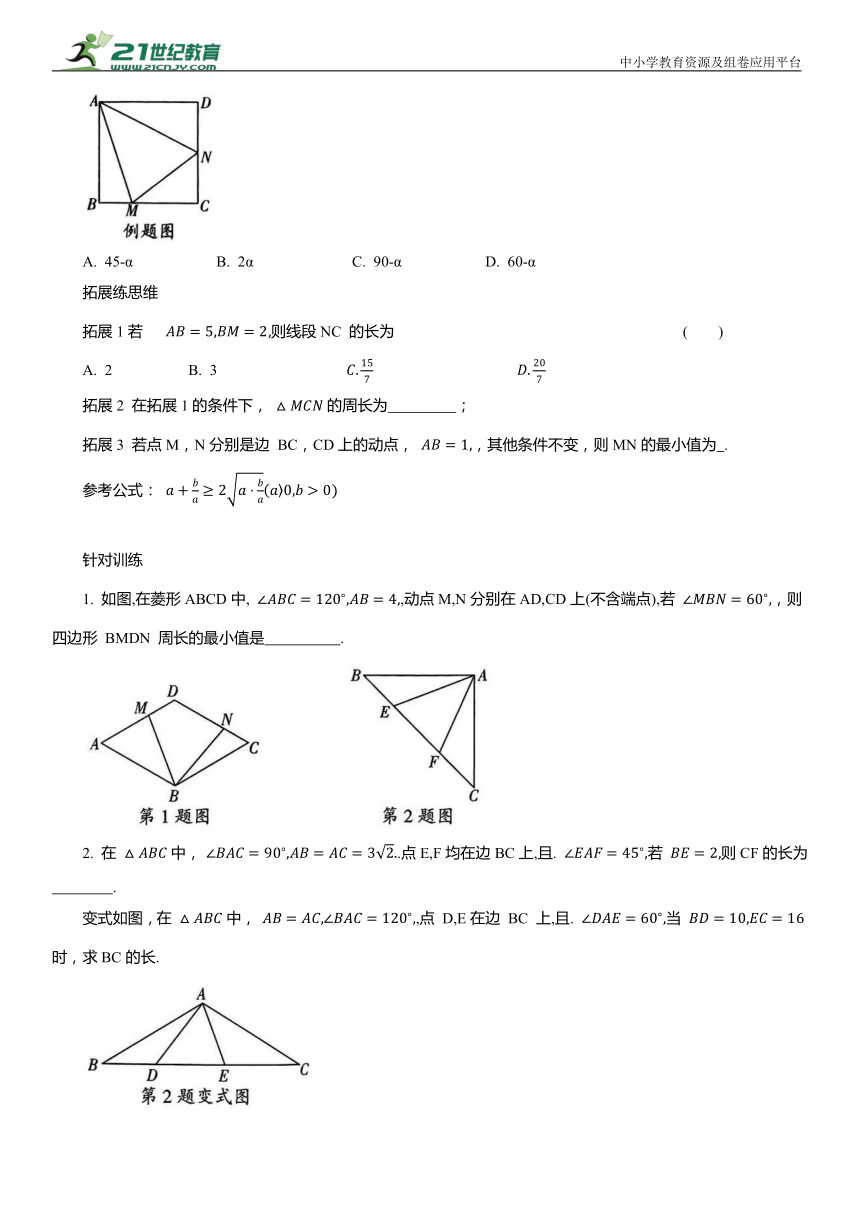
例 [2024大连沙河口区期末]如图,在正方形ABCD 中,点M,N分别在BC,CD上,且∠MAN=45°,连接MN.若∠BAM=α,则∠NMC的度数是 ( )
45-α B. 2α C. 90-α D. 60-α
拓展练思维
拓展1若 则线段NC 的长为 ( )
A. 2 B. 3
拓展2 在拓展1的条件下, 的周长为 ;
拓展3 若点M,N分别是边 BC,CD上的动点, ,其他条件不变,则MN的最小值为 .
参考公式:
针对训练
1. 如图,在菱形ABCD中, ,动点M,N分别在AD,CD上(不含端点),若 ,则四边形 BMDN 周长的最小值是 .
2. 在 中, .点E,F均在边BC上,且. 若 则CF的长为 .
变式如图,在 中, ,点 D,E在边 BC 上,且. 当 时,求BC的长.
中小学教育资源及组卷应用平台
模型三 半角模型
例 B 拓展1 D 拓展210
拓展32 -2 【解析】如解图,延长CB到点G,使BG=DN,连接AG.根据例题同理可得△GAM≌△NAM,∴GM=MN,设DN=x,MN=y,则GM=y,BG=x.∵BC=CD=AB=1,∴CN=1-x,CM=x-y+1,在Rt△CMN中,由勾股定理,得 即 整理可得 故MN的最小值为
【针对训练】
【解析】如解图,连接BD.∵四边形ABCD是菱形,AB=4,∠ABC=120°,∴BC=CD=AD=AB=4,∠ABD=∠CBD= ∠ABC=60°,∴△ABD,△BDC 都是等边三角形,∴∠BDM=∠BCN=60°,DB=CB,∵∠MBN=∠DBC=60°,∴ ∠DBM =∠CBN,∴△DBM≌△CBN(ASA),∴BM=BN,DM=CN,∴DM+DN=NC+DN=CD=4,∵四边形 BMDN的周长为 BM+DM+DN+BN=2BM+4,∴当BM的值最小时,四边形 BMDN的周长最小,根据垂线段最短可知,当BM⊥AD时,BM的值最小,此时BN=BM=AB· 四边形 BMDN周长的最小值为4 +4.
2. 【解析】如解图,把△ABE 绕点A 逆时针旋转 90°得△ACN,连接 FN,∴AN=AE,CN=BE=2,∠ACN=∠B,∠EAN=90°,∵ ∠BAC=90°,AB =AC=3 ,∴ ∠B= ∵∠EAF=45°,∴ ∠BAE+∠CAF= 90°-45°= 45°,∵∠BAE=∠CAN,∴ ∠FAN=∠EAF=45°,又∵AF=AF,AE=AN,∴△EAF≌△NAF(SAS),∴ EF=NF,设(CF=x,则NF=EF=4-x,在Rt△FCN中, 即(4- 解得 即
变式解:如解图,把△ACE 绕点 A 顺时针旋转120°得到△ABP,连接PD,
∴AP=AE,PB=CE=16,∠PBA=∠C,∠EAP=∠BAC=120°,
∵AB=AC,∠BAC=120°,
∴∠ABD=∠C=∠ABP=30°,
∴∠ABD+∠ABP=60°,即∠PBD=60°,
又∵∠DAE=60°,
∴ ∠PAD=∠EAP-∠DAE=120°-60°=60°,
在△AED和△APD中,
∴△AED≌△APD(SAS),
∴ED=PD,
过点D作DH⊥BP,垂足为H,
∴HP=BP-BH=16-5=11.
∴DE=PD=14,∴BC=BD+DE+EC=10+14+16=40.
模型解读
一个角包含着它一半大小的角,将这样的模型统称为半角模型.
基本模型
结论 ①△AEF≌△AEG;②EF=BE+DF;③连接GF,△AGF为等腰直角三角形
拓展模型 △ABC 为等腰直角三角形,∠BAC=90° 作法1: 将△ABD 绕点 A 逆时针旋转90°得△ACF 作法2: 将△ABD,△ACE 分别沿直线AD,AE 翻折,点B,C在点F处重合
结论 △ADE≌△AFE, ∠ECF=90°, BD=DF,CE=EF, ∠DFE=90°,
拓展模型 作法:将△ABD绕点A 逆时针旋转120°(60°)得到△ACD'
结论 △ADE≌△AD'E
例 [2024大连沙河口区期末]如图,在正方形ABCD 中,点M,N分别在BC,CD上,且∠MAN=45°,连接MN.若∠BAM=α,则∠NMC的度数是 ( )
45-α B. 2α C. 90-α D. 60-α
拓展练思维
拓展1若 则线段NC 的长为 ( )
A. 2 B. 3
拓展2 在拓展1的条件下, 的周长为 ;
拓展3 若点M,N分别是边 BC,CD上的动点, ,其他条件不变,则MN的最小值为 .
参考公式:
针对训练
1. 如图,在菱形ABCD中, ,动点M,N分别在AD,CD上(不含端点),若 ,则四边形 BMDN 周长的最小值是 .
2. 在 中, .点E,F均在边BC上,且. 若 则CF的长为 .
变式如图,在 中, ,点 D,E在边 BC 上,且. 当 时,求BC的长.
中小学教育资源及组卷应用平台
模型三 半角模型
例 B 拓展1 D 拓展210
拓展32 -2 【解析】如解图,延长CB到点G,使BG=DN,连接AG.根据例题同理可得△GAM≌△NAM,∴GM=MN,设DN=x,MN=y,则GM=y,BG=x.∵BC=CD=AB=1,∴CN=1-x,CM=x-y+1,在Rt△CMN中,由勾股定理,得 即 整理可得 故MN的最小值为
【针对训练】
【解析】如解图,连接BD.∵四边形ABCD是菱形,AB=4,∠ABC=120°,∴BC=CD=AD=AB=4,∠ABD=∠CBD= ∠ABC=60°,∴△ABD,△BDC 都是等边三角形,∴∠BDM=∠BCN=60°,DB=CB,∵∠MBN=∠DBC=60°,∴ ∠DBM =∠CBN,∴△DBM≌△CBN(ASA),∴BM=BN,DM=CN,∴DM+DN=NC+DN=CD=4,∵四边形 BMDN的周长为 BM+DM+DN+BN=2BM+4,∴当BM的值最小时,四边形 BMDN的周长最小,根据垂线段最短可知,当BM⊥AD时,BM的值最小,此时BN=BM=AB· 四边形 BMDN周长的最小值为4 +4.
2. 【解析】如解图,把△ABE 绕点A 逆时针旋转 90°得△ACN,连接 FN,∴AN=AE,CN=BE=2,∠ACN=∠B,∠EAN=90°,∵ ∠BAC=90°,AB =AC=3 ,∴ ∠B= ∵∠EAF=45°,∴ ∠BAE+∠CAF= 90°-45°= 45°,∵∠BAE=∠CAN,∴ ∠FAN=∠EAF=45°,又∵AF=AF,AE=AN,∴△EAF≌△NAF(SAS),∴ EF=NF,设(CF=x,则NF=EF=4-x,在Rt△FCN中, 即(4- 解得 即
变式解:如解图,把△ACE 绕点 A 顺时针旋转120°得到△ABP,连接PD,
∴AP=AE,PB=CE=16,∠PBA=∠C,∠EAP=∠BAC=120°,
∵AB=AC,∠BAC=120°,
∴∠ABD=∠C=∠ABP=30°,
∴∠ABD+∠ABP=60°,即∠PBD=60°,
又∵∠DAE=60°,
∴ ∠PAD=∠EAP-∠DAE=120°-60°=60°,
在△AED和△APD中,
∴△AED≌△APD(SAS),
∴ED=PD,
过点D作DH⊥BP,垂足为H,
∴HP=BP-BH=16-5=11.
∴DE=PD=14,∴BC=BD+DE+EC=10+14+16=40.
同课章节目录
