2025年中考数学培优模型五 手拉手模型(含解析)
文档属性
| 名称 | 2025年中考数学培优模型五 手拉手模型(含解析) | 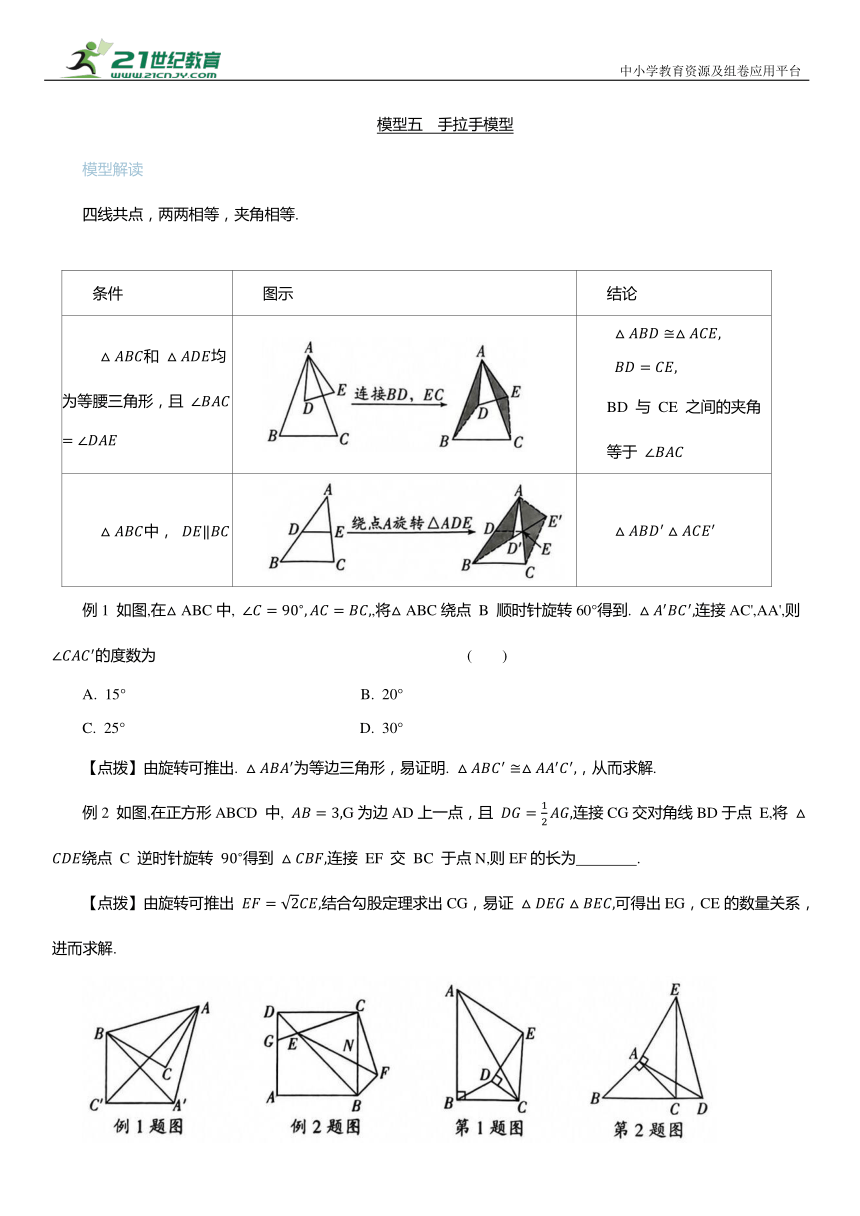 | |
| 格式 | docx | ||
| 文件大小 | 181.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 13:47:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
模型五 手拉手模型
模型解读
四线共点,两两相等,夹角相等.
条件 图示 结论
和 均为等腰三角形,且 BD 与 CE 之间的夹角 等于
中,
例1 如图,在△ABC中, ,将△ABC绕点 B 顺时针旋转60°得到. 连接AC',AA',则 的度数为 ( )
A. 15° B. 20°
C. 25° D. 30°
【点拨】由旋转可推出. 为等边三角形,易证明. ,从而求解.
例2 如图,在正方形ABCD 中, G为边AD上一点,且 连接CG交对角线BD于点 E,将 绕点 C 逆时针旋转 得到 连接 EF 交 BC 于点N,则EF的长为 .
【点拨】由旋转可推出 结合勾股定理求出CG,易证 可得出EG,CE的数量关系,进而求解.
针对训练
1. 如图,在 和 中, ,连接BD,AE,若 ,则AE的值为 .
2.如图, 和 都是等腰直角三角形,即 ,B,C,D三点在同一条直线上.若 则
模型五 手拉手模型
例1 A例2
【针对训练】
1. 4
2. -1 【解析】∵△ABC和△ADE都是等腰直角三角形, +∠CAD=∠DAE+∠CAD = ∠CAE,AB =AC,AD = AE,∴△ABD≌△ACE(SAS),∴ BD=CE,∠ABD =∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°=∠ECD.设CD=x,则BD=CE=2+x,在 Rt△ECD中,根据勾股定理得,CD + 即 解得 (负值已舍去),.
模型五 手拉手模型
模型解读
四线共点,两两相等,夹角相等.
条件 图示 结论
和 均为等腰三角形,且 BD 与 CE 之间的夹角 等于
中,
例1 如图,在△ABC中, ,将△ABC绕点 B 顺时针旋转60°得到. 连接AC',AA',则 的度数为 ( )
A. 15° B. 20°
C. 25° D. 30°
【点拨】由旋转可推出. 为等边三角形,易证明. ,从而求解.
例2 如图,在正方形ABCD 中, G为边AD上一点,且 连接CG交对角线BD于点 E,将 绕点 C 逆时针旋转 得到 连接 EF 交 BC 于点N,则EF的长为 .
【点拨】由旋转可推出 结合勾股定理求出CG,易证 可得出EG,CE的数量关系,进而求解.
针对训练
1. 如图,在 和 中, ,连接BD,AE,若 ,则AE的值为 .
2.如图, 和 都是等腰直角三角形,即 ,B,C,D三点在同一条直线上.若 则
模型五 手拉手模型
例1 A例2
【针对训练】
1. 4
2. -1 【解析】∵△ABC和△ADE都是等腰直角三角形, +∠CAD=∠DAE+∠CAD = ∠CAE,AB =AC,AD = AE,∴△ABD≌△ACE(SAS),∴ BD=CE,∠ABD =∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°=∠ECD.设CD=x,则BD=CE=2+x,在 Rt△ECD中,根据勾股定理得,CD + 即 解得 (负值已舍去),.
同课章节目录
