2025年中考数学培优模型六 对角互补模型(含十字模型)(含解析)
文档属性
| 名称 | 2025年中考数学培优模型六 对角互补模型(含十字模型)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 270.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
模型六 对角互补模型(含十字模型)
模型解读
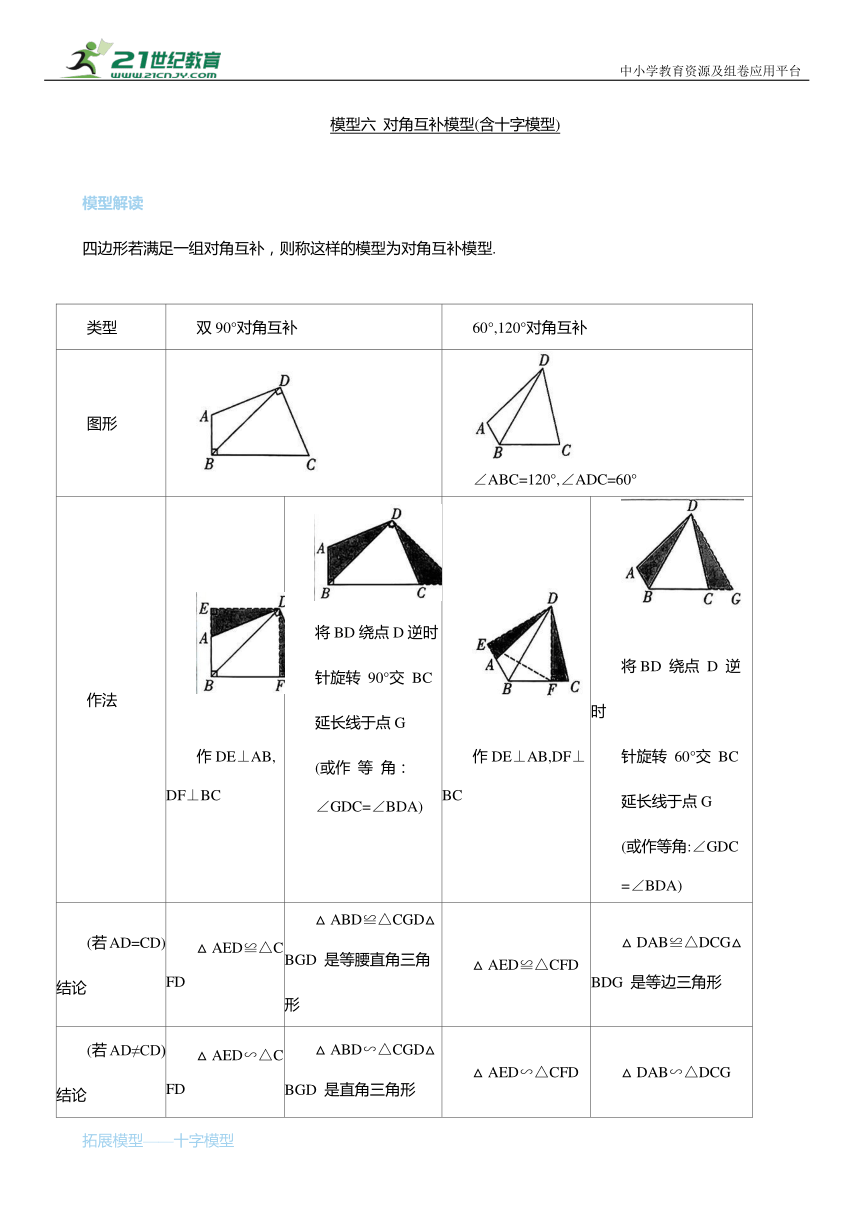
四边形若满足一组对角互补,则称这样的模型为对角互补模型.
类型 双90°对角互补 60°,120°对角互补
图形 ∠ABC=120°,∠ADC=60°
作法 作DE⊥AB,DF⊥BC 将BD绕点D逆时 针旋转 90°交 BC 延长线于点G (或作 等 角: ∠GDC=∠BDA) 作DE⊥AB,DF⊥BC 将BD 绕点 D 逆时 针旋转 60°交 BC 延长线于点G (或作等角:∠GDC =∠BDA)
(若AD=CD)结论 △AED≌△CFD △ABD≌△CGD△BGD 是等腰直角三角形 △AED≌△CFD △DAB≌△DCG△BDG 是等边三角形
(若AD≠CD)结论 △AED∽△CFD △ABD∽△CGD△BGD 是直角三角形 △AED∽△CFD △DAB∽△DCG
拓展模型——十字模型
基本图形 正方形 矩形
辅助线作法 过点 G 作 GH⊥AB 于点H 过点H作HN⊥BC 于点N,过点G作GM⊥AB 于点M
结论 DE=AF, △ADE≌△BAF GE=AF, △GHE≌△ABF GE=HF, △HFN≌△GEM △HFN∽△GEM, 相似比为矩形长与宽之比
例 如图①,正方形ABCD的边长为3,O是对角线AC上一点,且( E是边CD上一点,连接OE,过点O作 交BC于点 F.
(1)四边形 CEOF 的面积为 ;
【点拨】过点O分别作CD,BC的垂线,构造全等三角形,将四边形CEOF的面积转化为一个以OC 为对角线的正方形的面积.
(2)如图②,延长OE,AD 交于点M,延长OF,DC 交于点N,则
【点拨】过点O分别作AD,DC的垂线,构造相似三角形,将所求比值转化为相似三角形的相似比.
针对训练
1.90°对角互补多解法如图, 的顶点在 的角平分线 OC上,两边分别与射线OA,OB交于点D,E,若( ,则CE 的值为 .
对角互补 如图,在四边形ABCD中, ,若四边形AB-CD的面积为 则
3. 十字模型[2023 丹东16题3分]如图,在正方形ABCD中, ,点 E,F 分别在边 BC,CD上,AE与BF 相交于点 G,若. 则BG的长为 .
4.120°对角互补多解法如图,等边三角形ABC的边长为4,D是边AC的中点,点E 在边 AB上, ,点F 在边 BC的延长线上,且. 则CF的长为 .
模型六 对角互补模型(含十字模型)
例 (1)4 (2)
【针对训练】
1. 3 【解析】解法1:如解图①,过点 C 分别作 CM⊥OA,CN⊥OB 于点 M,N,由角平分线性质可得 CM=CN,∠MCN=90°,∴ ∠MCD=∠NCE,∴ △MCD≌△NCE,∴CD=CE=3.
解法2:如解图②,过点 C 作CF⊥OC,与OB 交于点F,易证∠DOC = ∠EFC = 45°,CO = CF,∠DCO =∠ECF,∴△DCO≌△ECF,∴CD=CE=3.
2. 4 3. 6
4. 1 【解析】解法1:如解图①,过点 D 作DG∥BC交AB于点G,∵△ABC是等边三角形,∴∠B=∠ACB=60°,AB=AC = BC,∴ ∠GDC = 120°= ∠EDF,∠EGD =120°=∠DCF,∴∠GDE=∠CDF,∵D是AC的中点,DG∥BC,∴ △CDF,∴GE=CF.∵ BE=1,∴GE=CF=1.
解法2:如解图②,过点 D 分别作 DM⊥AB 于点 M,DN⊥BC 于点N,连接 BD,∵△ABC 是等边三角形,D 是AC的中点,∴ BD 是∠ABC 的平分线,∴DM=DN,∵∠ABC=60°,∴ ∠MDN = 120°,∴∠MDE+∠NDE=∠NDE+∠NDF,∴∠MDE=∠NDF,∵∠DME=∠DNF=90°,∴ △DME≌△DNF(ASA),∴ ME = NF,在Rt△ADM中,AD=2,∠A=60°,∴AM=1,同理,CN=1,∴ME=AB-AM-BE=2,∴NF=2,∴CF=1.
模型六 对角互补模型(含十字模型)
模型解读
四边形若满足一组对角互补,则称这样的模型为对角互补模型.
类型 双90°对角互补 60°,120°对角互补
图形 ∠ABC=120°,∠ADC=60°
作法 作DE⊥AB,DF⊥BC 将BD绕点D逆时 针旋转 90°交 BC 延长线于点G (或作 等 角: ∠GDC=∠BDA) 作DE⊥AB,DF⊥BC 将BD 绕点 D 逆时 针旋转 60°交 BC 延长线于点G (或作等角:∠GDC =∠BDA)
(若AD=CD)结论 △AED≌△CFD △ABD≌△CGD△BGD 是等腰直角三角形 △AED≌△CFD △DAB≌△DCG△BDG 是等边三角形
(若AD≠CD)结论 △AED∽△CFD △ABD∽△CGD△BGD 是直角三角形 △AED∽△CFD △DAB∽△DCG
拓展模型——十字模型
基本图形 正方形 矩形
辅助线作法 过点 G 作 GH⊥AB 于点H 过点H作HN⊥BC 于点N,过点G作GM⊥AB 于点M
结论 DE=AF, △ADE≌△BAF GE=AF, △GHE≌△ABF GE=HF, △HFN≌△GEM △HFN∽△GEM, 相似比为矩形长与宽之比
例 如图①,正方形ABCD的边长为3,O是对角线AC上一点,且( E是边CD上一点,连接OE,过点O作 交BC于点 F.
(1)四边形 CEOF 的面积为 ;
【点拨】过点O分别作CD,BC的垂线,构造全等三角形,将四边形CEOF的面积转化为一个以OC 为对角线的正方形的面积.
(2)如图②,延长OE,AD 交于点M,延长OF,DC 交于点N,则
【点拨】过点O分别作AD,DC的垂线,构造相似三角形,将所求比值转化为相似三角形的相似比.
针对训练
1.90°对角互补多解法如图, 的顶点在 的角平分线 OC上,两边分别与射线OA,OB交于点D,E,若( ,则CE 的值为 .
对角互补 如图,在四边形ABCD中, ,若四边形AB-CD的面积为 则
3. 十字模型[2023 丹东16题3分]如图,在正方形ABCD中, ,点 E,F 分别在边 BC,CD上,AE与BF 相交于点 G,若. 则BG的长为 .
4.120°对角互补多解法如图,等边三角形ABC的边长为4,D是边AC的中点,点E 在边 AB上, ,点F 在边 BC的延长线上,且. 则CF的长为 .
模型六 对角互补模型(含十字模型)
例 (1)4 (2)
【针对训练】
1. 3 【解析】解法1:如解图①,过点 C 分别作 CM⊥OA,CN⊥OB 于点 M,N,由角平分线性质可得 CM=CN,∠MCN=90°,∴ ∠MCD=∠NCE,∴ △MCD≌△NCE,∴CD=CE=3.
解法2:如解图②,过点 C 作CF⊥OC,与OB 交于点F,易证∠DOC = ∠EFC = 45°,CO = CF,∠DCO =∠ECF,∴△DCO≌△ECF,∴CD=CE=3.
2. 4 3. 6
4. 1 【解析】解法1:如解图①,过点 D 作DG∥BC交AB于点G,∵△ABC是等边三角形,∴∠B=∠ACB=60°,AB=AC = BC,∴ ∠GDC = 120°= ∠EDF,∠EGD =120°=∠DCF,∴∠GDE=∠CDF,∵D是AC的中点,DG∥BC,∴ △CDF,∴GE=CF.∵ BE=1,∴GE=CF=1.
解法2:如解图②,过点 D 分别作 DM⊥AB 于点 M,DN⊥BC 于点N,连接 BD,∵△ABC 是等边三角形,D 是AC的中点,∴ BD 是∠ABC 的平分线,∴DM=DN,∵∠ABC=60°,∴ ∠MDN = 120°,∴∠MDE+∠NDE=∠NDE+∠NDF,∴∠MDE=∠NDF,∵∠DME=∠DNF=90°,∴ △DME≌△DNF(ASA),∴ ME = NF,在Rt△ADM中,AD=2,∠A=60°,∴AM=1,同理,CN=1,∴ME=AB-AM-BE=2,∴NF=2,∴CF=1.
同课章节目录
