2025年中考数学培优模型七 与圆有关的模型(含答案)
文档属性
| 名称 | 2025年中考数学培优模型七 与圆有关的模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 480.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 11:29:26 | ||
图片预览



文档简介
模型七 与圆有关的模型
类型①点圆、线圆最值模型
模型解读 点圆最值(记⊙O半径为r)
图形 定点在圆外 定点在圆上 定点在圆内
解法提炼 基本方法:“一箭穿心”找最值,“近”最小,“远”最大 基本依据:三角形三边关系及三点共线,圆中最长弦是直径
最值 最大值为 最小值为 最大值为 最小值为 最大值为 最小值为
模型解读线圆最值(记⊙O 半径为r,圆心O到定直线 m的距离为d)
图形 线圆相离 线圆相切 线圆相交
依据与总结 依据1:垂线段最短 依据2:三角形三边关系及三点共线 总结:过圆心作定直线的垂线与圆相交,“近垂足”取最小,“远垂足”取最大
最值
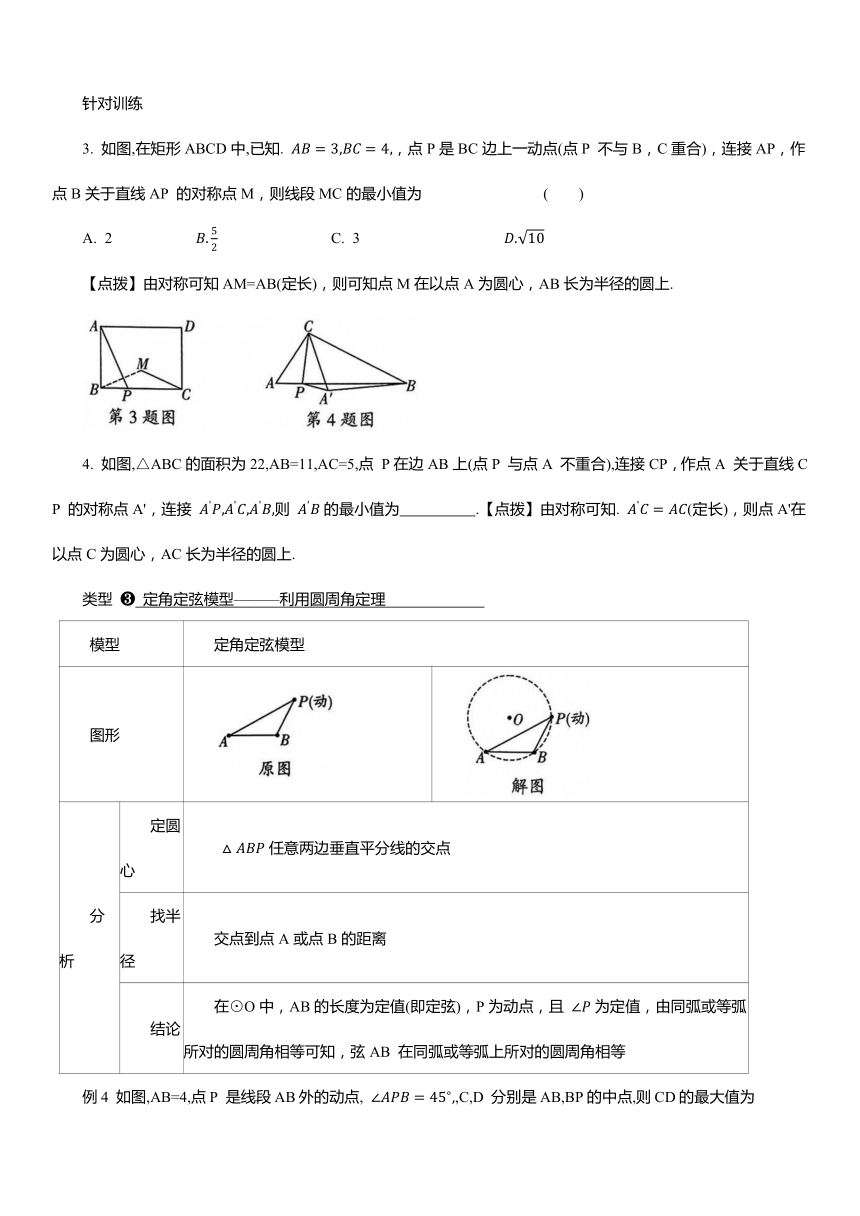
例1 如图,在 中, ,以BC为直径的半圆交AB 于点 D,点 P是弧CD上的一个动点,连接AP,则AP 的最小值是 .
草图区:
【点拨】当点P在OA上时,即点A,P,O三点共线时,AP 最短.
例2 如图,AB是⊙O的弦,C是⊙O上异于A,B的一动点,连接AC,BC,若⊙O的半径为5, ,则点 C到AB距离的最大值为 , \triangle A B C面积的最大值为 .
【点拨】AB 为弦,即直线AB与圆相交,过点C作AB 的垂线,当垂线经过圆心时,点C到AB的距离最大.当点 C 到AB的距离最大时, 的面积最大.
草图区:
针对训练
1. 如图,AB是⊙O 的直径,半径OC⊥AB,点 P 为⊙O 上一动点,M为AP 的中点,连接CM,OP.若⊙O 的半径为2,则 CM的最大值为 ( )
C. 4
2. 如图,A,B是半径为2的⊙O上的两点,且 点C为⊙O上一动点(不与点A,B 重合),则△ABC 面积的最大值为 ( )
类型 定点定长模型————利用圆定义
模型 定点定长模型
图形
分析 定圆心 三条等长线段的公共点A
找半径 AB(或AC)
结论 已知平面内一定点A和一动点P,若AP长度固定,且 则动点P的轨迹是以点A 为圆心,AP 长为半径的圆
例3 如图,在四边形 ABCD 中,AB = AC = AD,∠CAD=2∠BAC,若. 则
【点拨】由AB=AC=AD 可得,点B,C,D在以点A为圆心,AB长为半径的圆上.
中小学教育资源及组卷应用平台
草图区:
针对训练
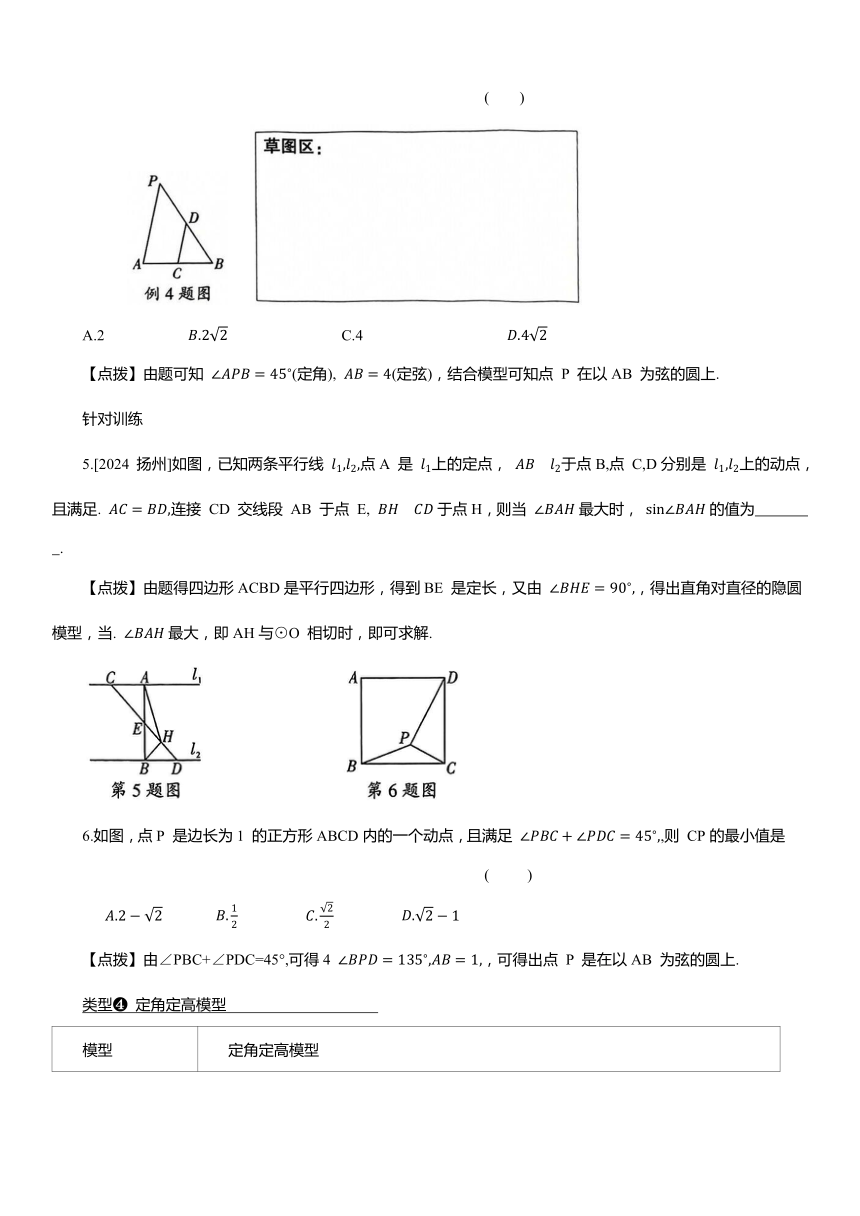
3. 如图,在矩形ABCD中,已知. ,点P是BC边上一动点(点P 不与B,C重合),连接AP,作点B关于直线AP 的对称点M,则线段MC的最小值为 ( )
A. 2 C. 3
【点拨】由对称可知AM=AB(定长),则可知点M在以点A为圆心,AB长为半径的圆上.
4. 如图,△ABC的面积为22,AB=11,AC=5,点 P在边AB上(点P 与点A 不重合),连接CP,作点A 关于直线CP 的对称点A',连接 则 的最小值为 .【点拨】由对称可知. (定长),则点A'在以点C为圆心,AC长为半径的圆上.
类型 定角定弦模型———利用圆周角定理
模型 定角定弦模型
图形
分析 定圆心 任意两边垂直平分线的交点
找半径 交点到点A或点B的距离
结论 在⊙O中,AB的长度为定值(即定弦),P为动点,且 为定值,由同弧或等弧所对的圆周角相等可知,弦AB 在同弧或等弧上所对的圆周角相等
例4 如图,AB=4,点P 是线段AB外的动点, ,C,D 分别是AB,BP的中点,则CD的最大值为 ( )
A.2 C.4
【点拨】由题可知 (定角), (定弦),结合模型可知点 P 在以AB 为弦的圆上.
针对训练
5.[2024 扬州]如图,已知两条平行线 点A 是 上的定点, 于点B,点 C,D分别是 上的动点,且满足. 连接 CD 交线段 AB 于点 E, 于点H,则当 最大时, 的值为 .
【点拨】由题得四边形ACBD是平行四边形,得到BE 是定长,又由 ,得出直角对直径的隐圆模型,当. 最大,即AH与⊙O 相切时,即可求解.
6.如图,点P 是边长为1 的正方形ABCD内的一个动点,且满足 ,则 CP的最小值是 ( )
【点拨】由∠PBC+∠PDC=45°,可得4 ,可得出点 P 是在以AB 为弦的圆上.
类型 定角定高模型
模型 定角定高模型
图形
分析 定圆心 三边垂直平分线的交点
找半径 交点到点B或点A或点C的距离
结论 已知在 中, 的值为定值(即定角),BD为边AC 上的高,则点B 可看作在圆上运动,当B,O,H三点共线时,AC 有最小值
例5 多解法如图,在 中, ,BC 边上的高. 则 周长的最小值为 .
【速解技巧】当直接应用定高模型的结论时可快速解题.
针对训练
7. 如图,在△ABC中,∠ABC=120°,BD⊥AC于点D, ,则AC的最小值是( )
A. 5
变式若∠ABC=60°,BD=4,则△ABC 面积的最小值为 .
类型 四点共圆模型
模型 四点共圆模型
图形
分析 已知 已知动角∠A+动角, 已知AB 的长度为定值,且线段AB所对同侧动角.
定圆心 四边形 ABCD 任意两边垂直平分线的交点 或 任意两边垂直平分线的交点
找半径 交点到点B或点D的距离 交点到点A或点B或点C的距离
结论 对角互补四边形的四个顶点共圆(圆内接四边形性质) 共边三角形且边所对角相等的四个顶点共圆(同弧所对的圆周角相等)
例6 如图,以 C 为公共顶点的 Rt△ABC 和 Rt△CED 中, ∠DCE=30°,且点 D 在线段AB上,则∠ABE= .
针对训练
8.[2023本溪明山区月考]如图,以量角器的直径AB为斜边画直角三角形ABC,量角器上点D对应的读数是 ,则∠BCD 的度数为 ( )
A. 30° B. 40° C. 50°
9. 如图,在△ABC中,BD,CE分别是AC,AB 边上的高,已知 则 DE 的长为 .
模型七与圆有关的模型
例1 -1
例2 8;32 【解析】如解图,连接OA,过点O作AB的垂线,垂足为D,延长DO 交⊙O 于点 ∴在 Rt△AOD中,( 点C到AB距离的最大值为8,∴△ABC面积的最大值为
【针对训练】
1. B 【解析】如解图,当点 P在⊙O 上运动时,取OA 的中点O',连接O'M,则O'M是△AOP的中位线,∴O'M=1,∴AP 的中点 M 的轨迹是以OA为直径的⊙O',即点 M 在以O'为圆心,半径为1的圆上运动,此时CO'交⊙O'于点M,CM的值最大,由题意得OA=OB=OC=2,OO'=O'A=1=0'M,∵ 在 Rt△O'OC 中,
2. C 【解析】如解图,边点O 作OH⊥AB于点H,连接OA,延长HO交⊙O 于点 C,此时△ABC的面积最大,∴AH=BH= 1,∴CH=OC+OH=2+1=3,∴△ABC 的面积为 面积的最大值为3
例3 25
【针对训练】
3. A
4. 4 -5 【解析】如解图,过点C作CD⊥AB,垂足为点D,∵△ABC的面积为22,AB=11,∴ CD=4,在 Rt△ACD中,∵AC=5,CD=4,∴AD=3,∴BD=AB-AD=8,在Rt△BCD中,∵CD=4,BD=8,∴BC=4 ,∵点A和点A'关于直线CP 对称,∴点A'在以点 C 为圆心,AC长为半径的圆上,AC=A'C=5,∴A'B≥BC-A'C,∴A'B的最小值为
例4 B
【针对训练】
5. 【解析】如解图,连接CB,AD,∵AC∥BD,AC=BD,∴四边形ACBD是平行四边形,∴ ∵A为定点,且AB⊥l ,∴AB为定值,∴BE为定值,∵ BH⊥CD,∴∠BHE=90°,∴点H在以 BE为直径的⊙O 上运动,此时 ∵当AH与⊙O 相切时,∠BAH最大
6. D 【解析】∵四边形ABCD 是正方形,∴∠BCD=90°,在四边形BCDP中,∵∠BCD=90°,∠PBC+∠PDC=45°,∴∠BPC+∠CPD=360°-∠BCD-(∠PBC+∠PDC)=225°, ,即点P在正方形ABCD内,以点A为圆心,AB 长为半径的圆弧上,如解图,可得AP+CP≥AC,当点A,P,C三点共线时,CP 取得最小值,最小值为AC-AP,在 Rt△ABC中,∵AB=BC=1,
例5 8+8 【解析】解法1:如解图①,延长CB到点E,延长BC到点 F,使得BE=BA,CF=CA,则( =EB+BC+CF=EF.作出△AEF的外接圆,连接OE,OF,过点O作 EF的垂线,垂足为M,与⊙O 交于点 N,∵AB=EB,AC=FC,∴∠AEB=∠EAB,∠CAF=∠CFA,∴∠ABC=2∠AEB,∠ACB =2∠AFC. ∵ ∠BAC =90°,∴ ∠ABC+∠ACB=90°,∴ ∠AEB+∠AFC=45°,∴ ∠EAB+∠FAC=45°,∴∠EAF=135°,∴∠EOF=2×(180°-135°)=90°.设⊙O的半径为r,则 由 MN≥AD得 解得 . r的最小值为 又 ∴ EF的最小值为8+8 ,即△ABC周长的最小值为
解法2:如解图②,由定角定高的结论知,当AB=AC时,△ABC 的周长最小,∵AD=4,∠BAC=90°,易得BC=2AD=8,AB=AC=4 ,即△ABC周长的最小值为
【针对训练】
7. B 【解析】如解图,作△ABC的外接圆⊙O,连接OA,OB,OC,过点O作OH⊥AC 于点 H,∵∠ABC=120°,∴∠AOC=2×(180°-∠ABC)=120°,∴∠AOH=60°,设⊙O的半径为r,则 又∵OB≥OH+BD,即 解得 AC的最小值为6
变式 【解析】如解图,作△ABC的外接圆⊙O,连接OA,OB,OC,过点 O 作 OE⊥AC 于点 E,∵ ∠ABC=60°,∴∠AOC=120°,∵OA=OC,∴∠OAC=∠OCA=30°,设⊙O的半径为r,则 解得 ∴△ABC面积的最小值为
例6 30°
【针对训练】
8. B 9. 3
类型①点圆、线圆最值模型
模型解读 点圆最值(记⊙O半径为r)
图形 定点在圆外 定点在圆上 定点在圆内
解法提炼 基本方法:“一箭穿心”找最值,“近”最小,“远”最大 基本依据:三角形三边关系及三点共线,圆中最长弦是直径
最值 最大值为 最小值为 最大值为 最小值为 最大值为 最小值为
模型解读线圆最值(记⊙O 半径为r,圆心O到定直线 m的距离为d)
图形 线圆相离 线圆相切 线圆相交
依据与总结 依据1:垂线段最短 依据2:三角形三边关系及三点共线 总结:过圆心作定直线的垂线与圆相交,“近垂足”取最小,“远垂足”取最大
最值
例1 如图,在 中, ,以BC为直径的半圆交AB 于点 D,点 P是弧CD上的一个动点,连接AP,则AP 的最小值是 .
草图区:
【点拨】当点P在OA上时,即点A,P,O三点共线时,AP 最短.
例2 如图,AB是⊙O的弦,C是⊙O上异于A,B的一动点,连接AC,BC,若⊙O的半径为5, ,则点 C到AB距离的最大值为 , \triangle A B C面积的最大值为 .
【点拨】AB 为弦,即直线AB与圆相交,过点C作AB 的垂线,当垂线经过圆心时,点C到AB的距离最大.当点 C 到AB的距离最大时, 的面积最大.
草图区:
针对训练
1. 如图,AB是⊙O 的直径,半径OC⊥AB,点 P 为⊙O 上一动点,M为AP 的中点,连接CM,OP.若⊙O 的半径为2,则 CM的最大值为 ( )
C. 4
2. 如图,A,B是半径为2的⊙O上的两点,且 点C为⊙O上一动点(不与点A,B 重合),则△ABC 面积的最大值为 ( )
类型 定点定长模型————利用圆定义
模型 定点定长模型
图形
分析 定圆心 三条等长线段的公共点A
找半径 AB(或AC)
结论 已知平面内一定点A和一动点P,若AP长度固定,且 则动点P的轨迹是以点A 为圆心,AP 长为半径的圆
例3 如图,在四边形 ABCD 中,AB = AC = AD,∠CAD=2∠BAC,若. 则
【点拨】由AB=AC=AD 可得,点B,C,D在以点A为圆心,AB长为半径的圆上.
中小学教育资源及组卷应用平台
草图区:
针对训练
3. 如图,在矩形ABCD中,已知. ,点P是BC边上一动点(点P 不与B,C重合),连接AP,作点B关于直线AP 的对称点M,则线段MC的最小值为 ( )
A. 2 C. 3
【点拨】由对称可知AM=AB(定长),则可知点M在以点A为圆心,AB长为半径的圆上.
4. 如图,△ABC的面积为22,AB=11,AC=5,点 P在边AB上(点P 与点A 不重合),连接CP,作点A 关于直线CP 的对称点A',连接 则 的最小值为 .【点拨】由对称可知. (定长),则点A'在以点C为圆心,AC长为半径的圆上.
类型 定角定弦模型———利用圆周角定理
模型 定角定弦模型
图形
分析 定圆心 任意两边垂直平分线的交点
找半径 交点到点A或点B的距离
结论 在⊙O中,AB的长度为定值(即定弦),P为动点,且 为定值,由同弧或等弧所对的圆周角相等可知,弦AB 在同弧或等弧上所对的圆周角相等
例4 如图,AB=4,点P 是线段AB外的动点, ,C,D 分别是AB,BP的中点,则CD的最大值为 ( )
A.2 C.4
【点拨】由题可知 (定角), (定弦),结合模型可知点 P 在以AB 为弦的圆上.
针对训练
5.[2024 扬州]如图,已知两条平行线 点A 是 上的定点, 于点B,点 C,D分别是 上的动点,且满足. 连接 CD 交线段 AB 于点 E, 于点H,则当 最大时, 的值为 .
【点拨】由题得四边形ACBD是平行四边形,得到BE 是定长,又由 ,得出直角对直径的隐圆模型,当. 最大,即AH与⊙O 相切时,即可求解.
6.如图,点P 是边长为1 的正方形ABCD内的一个动点,且满足 ,则 CP的最小值是 ( )
【点拨】由∠PBC+∠PDC=45°,可得4 ,可得出点 P 是在以AB 为弦的圆上.
类型 定角定高模型
模型 定角定高模型
图形
分析 定圆心 三边垂直平分线的交点
找半径 交点到点B或点A或点C的距离
结论 已知在 中, 的值为定值(即定角),BD为边AC 上的高,则点B 可看作在圆上运动,当B,O,H三点共线时,AC 有最小值
例5 多解法如图,在 中, ,BC 边上的高. 则 周长的最小值为 .
【速解技巧】当直接应用定高模型的结论时可快速解题.
针对训练
7. 如图,在△ABC中,∠ABC=120°,BD⊥AC于点D, ,则AC的最小值是( )
A. 5
变式若∠ABC=60°,BD=4,则△ABC 面积的最小值为 .
类型 四点共圆模型
模型 四点共圆模型
图形
分析 已知 已知动角∠A+动角, 已知AB 的长度为定值,且线段AB所对同侧动角.
定圆心 四边形 ABCD 任意两边垂直平分线的交点 或 任意两边垂直平分线的交点
找半径 交点到点B或点D的距离 交点到点A或点B或点C的距离
结论 对角互补四边形的四个顶点共圆(圆内接四边形性质) 共边三角形且边所对角相等的四个顶点共圆(同弧所对的圆周角相等)
例6 如图,以 C 为公共顶点的 Rt△ABC 和 Rt△CED 中, ∠DCE=30°,且点 D 在线段AB上,则∠ABE= .
针对训练
8.[2023本溪明山区月考]如图,以量角器的直径AB为斜边画直角三角形ABC,量角器上点D对应的读数是 ,则∠BCD 的度数为 ( )
A. 30° B. 40° C. 50°
9. 如图,在△ABC中,BD,CE分别是AC,AB 边上的高,已知 则 DE 的长为 .
模型七与圆有关的模型
例1 -1
例2 8;32 【解析】如解图,连接OA,过点O作AB的垂线,垂足为D,延长DO 交⊙O 于点 ∴在 Rt△AOD中,( 点C到AB距离的最大值为8,∴△ABC面积的最大值为
【针对训练】
1. B 【解析】如解图,当点 P在⊙O 上运动时,取OA 的中点O',连接O'M,则O'M是△AOP的中位线,∴O'M=1,∴AP 的中点 M 的轨迹是以OA为直径的⊙O',即点 M 在以O'为圆心,半径为1的圆上运动,此时CO'交⊙O'于点M,CM的值最大,由题意得OA=OB=OC=2,OO'=O'A=1=0'M,∵ 在 Rt△O'OC 中,
2. C 【解析】如解图,边点O 作OH⊥AB于点H,连接OA,延长HO交⊙O 于点 C,此时△ABC的面积最大,∴AH=BH= 1,∴CH=OC+OH=2+1=3,∴△ABC 的面积为 面积的最大值为3
例3 25
【针对训练】
3. A
4. 4 -5 【解析】如解图,过点C作CD⊥AB,垂足为点D,∵△ABC的面积为22,AB=11,∴ CD=4,在 Rt△ACD中,∵AC=5,CD=4,∴AD=3,∴BD=AB-AD=8,在Rt△BCD中,∵CD=4,BD=8,∴BC=4 ,∵点A和点A'关于直线CP 对称,∴点A'在以点 C 为圆心,AC长为半径的圆上,AC=A'C=5,∴A'B≥BC-A'C,∴A'B的最小值为
例4 B
【针对训练】
5. 【解析】如解图,连接CB,AD,∵AC∥BD,AC=BD,∴四边形ACBD是平行四边形,∴ ∵A为定点,且AB⊥l ,∴AB为定值,∴BE为定值,∵ BH⊥CD,∴∠BHE=90°,∴点H在以 BE为直径的⊙O 上运动,此时 ∵当AH与⊙O 相切时,∠BAH最大
6. D 【解析】∵四边形ABCD 是正方形,∴∠BCD=90°,在四边形BCDP中,∵∠BCD=90°,∠PBC+∠PDC=45°,∴∠BPC+∠CPD=360°-∠BCD-(∠PBC+∠PDC)=225°, ,即点P在正方形ABCD内,以点A为圆心,AB 长为半径的圆弧上,如解图,可得AP+CP≥AC,当点A,P,C三点共线时,CP 取得最小值,最小值为AC-AP,在 Rt△ABC中,∵AB=BC=1,
例5 8+8 【解析】解法1:如解图①,延长CB到点E,延长BC到点 F,使得BE=BA,CF=CA,则( =EB+BC+CF=EF.作出△AEF的外接圆,连接OE,OF,过点O作 EF的垂线,垂足为M,与⊙O 交于点 N,∵AB=EB,AC=FC,∴∠AEB=∠EAB,∠CAF=∠CFA,∴∠ABC=2∠AEB,∠ACB =2∠AFC. ∵ ∠BAC =90°,∴ ∠ABC+∠ACB=90°,∴ ∠AEB+∠AFC=45°,∴ ∠EAB+∠FAC=45°,∴∠EAF=135°,∴∠EOF=2×(180°-135°)=90°.设⊙O的半径为r,则 由 MN≥AD得 解得 . r的最小值为 又 ∴ EF的最小值为8+8 ,即△ABC周长的最小值为
解法2:如解图②,由定角定高的结论知,当AB=AC时,△ABC 的周长最小,∵AD=4,∠BAC=90°,易得BC=2AD=8,AB=AC=4 ,即△ABC周长的最小值为
【针对训练】
7. B 【解析】如解图,作△ABC的外接圆⊙O,连接OA,OB,OC,过点O作OH⊥AC 于点 H,∵∠ABC=120°,∴∠AOC=2×(180°-∠ABC)=120°,∴∠AOH=60°,设⊙O的半径为r,则 又∵OB≥OH+BD,即 解得 AC的最小值为6
变式 【解析】如解图,作△ABC的外接圆⊙O,连接OA,OB,OC,过点 O 作 OE⊥AC 于点 E,∵ ∠ABC=60°,∴∠AOC=120°,∵OA=OC,∴∠OAC=∠OCA=30°,设⊙O的半径为r,则 解得 ∴△ABC面积的最小值为
例6 30°
【针对训练】
8. B 9. 3
同课章节目录
