【中考模拟题汇编】查漏补缺:四边形-2025年中考数学(含答案)
文档属性
| 名称 | 【中考模拟题汇编】查漏补缺:四边形-2025年中考数学(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 05:35:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【中考模拟题汇编】查漏补缺:四边形-2025年中考数学
一.选择题(共8小题)
1.(2025 中山区一模)若正多边形的一个内角是120°,则这个正多边形的边数为( )
A.8 B.7 C.6 D.5
2.(2025 阜平县校级一模)如图,在 ABCD中,BE⊥AB交对角线AC于点E.若∠2=130°,则∠1的度数为( )
A.30° B.40° C.45° D.50°
3.(2025 昭阳区校级模拟)如图,在 ABCD中,∠ADC的平分线DE交BC于点E,若AB=11,BE=4,则AD的长为( )
A.15 B.11 C.20 D.52
4.(2025 石狮市模拟)依据所标数据,下列四边形不一定为菱形的是( )
A. B.
C. D.
5.(2025 重庆模拟)如图,在四边形ABCD中,AD∥BC,∠A=90°,AD=16,BC=21,CD=13,动点P从点B出发,沿射线BC以每秒3个单位的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位的速度向终点D运动,当动点Q到达点D时,动点P也同时停止运动.设点P的运动时间为t(秒).以点P、C、D、Q为顶点的四边形是平行四边形时t值为( )秒.
A.2或 B. C.或 D.
6.(2025 龙泉市二模)在正方形ABCD中,AB=6,P是对角线AC上一动点,作PE⊥AD于点E,PF⊥CD于点F.若四边形PFDE的面积为6,则BP的长为( )
A.4 B. C. D.
7.(2025 九龙坡区校级二模)如图,在正方形ABCD中,点E、F、G分别在AB、BC、CD上,连接AF、EG交于点H,连接CH,若CF=CG,AE=2DG,∠BAF=α,则∠HCF的度数为( )
A.45°+α B.45°﹣α C.2α D.α
8.(2025 涪城区三模)如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,AD上,且AE=DF,连接BF,交DE于点G,连接GC.现有下列结论:①∠BGD=120°;②GC平分∠BGD;③CG=DG+BG;④S四边形DGBCCG2.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题)
9.(2025 南岸区模拟)如果一个多边形的内角和是它的外角和的4倍,那么这个多边形的边数为 .
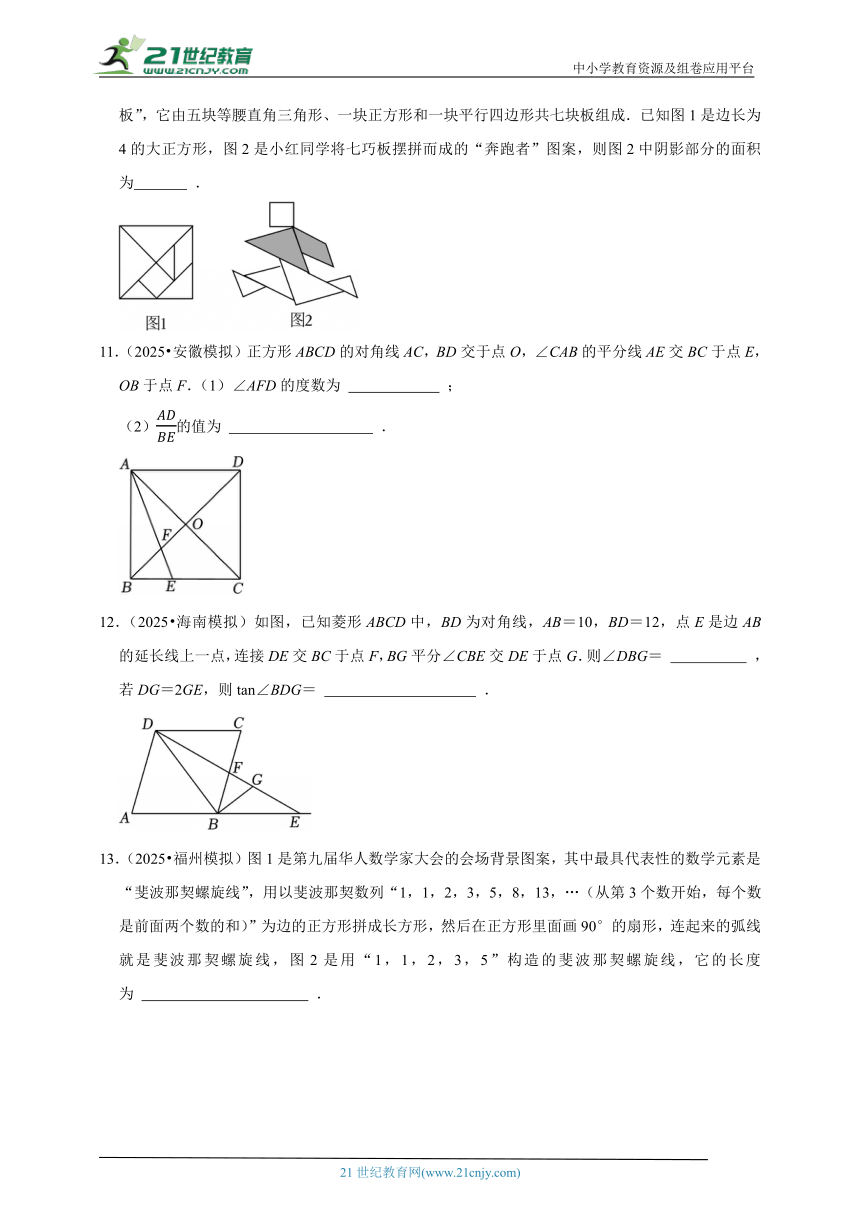
10.(2025 东莞市校级一模)七巧板是中国古代劳动人民发明的一种传统智力玩具,被誉为“东方魔板”,它由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成.已知图1是边长为4的大正方形,图2是小红同学将七巧板摆拼而成的“奔跑者”图案,则图2中阴影部分的面积为 .
11.(2025 安徽模拟)正方形ABCD的对角线AC,BD交于点O,∠CAB的平分线AE交BC于点E,OB于点F.(1)∠AFD的度数为 ;
(2)的值为 .
12.(2025 海南模拟)如图,已知菱形ABCD中,BD为对角线,AB=10,BD=12,点E是边AB的延长线上一点,连接DE交BC于点F,BG平分∠CBE交DE于点G.则∠DBG= ,若DG=2GE,则tan∠BDG= .
13.(2025 福州模拟)图1是第九届华人数学家大会的会场背景图案,其中最具代表性的数学元素是“斐波那契螺旋线”,用以斐波那契数列“1,1,2,3,5,8,13,…(从第3个数开始,每个数是前面两个数的和)”为边的正方形拼成长方形,然后在正方形里面画90°的扇形,连起来的弧线就是斐波那契螺旋线,图2是用“1,1,2,3,5”构造的斐波那契螺旋线,它的长度为 .
14.(2025 杭州模拟)如图,已知矩形ABCD中,点H是CD的中点,连结BD和AH交于点G,过A作BD的垂线交BD于点E,延长AE交BC于点F.若AB=BG,在BD上取一点P(不与B和D重合),使得直线CP刚好经过四边形DEFH某一条边的中点,则BP:BD的值为 .
三.解答题(共7小题)
15.(2025 镇平县模拟)如图,平行四边形ABCD中,点F在AD上.
(1)请用无刻度的直尺和圆规作AE⊥BC于点E.(保留作图痕迹,不写作法);
(2)若DF=BE,连接CF,求证:四边形AECF是矩形.
16.(2025 沛县二模)如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,过点C作CF∥AB,交DE延长线于点F,连接AF、CD.
(1)求证:四边形ADCF是菱形;
(2)当 时,四边形ADCF是正方形.
17.(2025 道里区二模)四边形ABCD为正方形,点E,F分别在BC,CD上,连接BF,DE,∠ADE=∠ABF.
(1)如图1,求证:DE=BF;
(2)如图2,设BF与DE交于点G,∠ABF=2∠CBF,在不添加任何辅助线的情况下,请写出图中所有等于的线段.
18.(2025 儋州模拟)已知正方形ABCD,一等腰直角三角形EFG的斜边EG经过其顶点B,直角边GF所在直线经过其顶点A(点B不与E,G重合,点A不与F,G重合),∠EFG=90°,EF=FG=6,,连接CG.
(1)如图1,若点B为EG的中点,且边GF的延长线经过顶点A时,连接BF.求∠BGC的度数.
(2)如图2,若顶点B不是EG中点,且顶点A在边FG上时,作CM⊥EG于点M,BE,.
①求∠BGC的度数;
②连接AC,交BG于点P,求CP的长.
19.(2025 泌阳县二模)在学习特殊四边形的过程中,我们对四边形有一些了解,并积累了一定的研究经验.定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.请运用已有经验,对“邻等对补四边形”进行研究.
(1)概念理解
①在以下四种图形中,一定是邻等对补四边形的是 ;
A.平行四边形
B.菱形
C.矩形
D.正方形
②分别用含有30°和45°角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有 .(填序号)
(2)概念应用
如图2,∠BAD=60°,且AB=AD.请你用尺规作图在平面内找出动点C的轨迹,使得四边形ABCD总是邻等对补四边形.(保留作图痕迹,不写作法)
(3)综合探究
在(2)的基础上,连接AC,探究线段AC,BC,CD之间满足的数量关系.
20.(2025 安州区三模)如图,在△ABC中,AC=5,CD为AB边上的高,且CD=BD,tan∠CAB,E,M为AC边上两个不重合的动点(点E在点M的上方,且均不与端点重合),EF∥AB,与边BC交于点F,四边形EMNF为平行四边形,连接BN.
(1)求AD,BD的长.
(2)如图①,若四边形EMNF为菱形,点N在CD上,当tan∠ABN时,求该菱形的边长.
(3)如图②,若BF=BN,则当EF长为多少时,平行四边形EMNF的面积取得最大值?求出最大值.
21.(2025 姑苏区校级二模)实践探究:两位同学利用菱形纸片进行翻折问题的自主探究,已知纸片为菱形ABCD,其边长为4,一个内角∠A=60°.
(1)如图1,他们将△AMN沿直线MN翻折得到△EMN,使得点E正好落在边CD上,且EM⊥AB,两位同学发现了不同的解法来求出图中线段DN的长度,一位同学找到了图中的一个特殊的等腰三角形,另一位同学则利用轴对称图形对应边相等这一性质;请聪明的你利用提示来求出线段DN的长度;
(2)如图2,两位同学又将△APQ沿直线PQ翻折得到△FPQ,使得点F正好是边CD的中点,那么此时线段DQ的长度是多少呢?
(3)如图3,点G为BC边上一点,将△ABG沿直线AG翻折得到△AKG,BK,AK的延长线分别交CD于S,T两点,若,求线段ST的长度.
【中考模拟题汇编】查漏补缺:四边形-2025年中考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C B A C C C B D
一.选择题(共8小题)
1.(2025 中山区一模)若正多边形的一个内角是120°,则这个正多边形的边数为( )
A.8 B.7 C.6 D.5
【解答】解:设所求正n边形边数为n,
则120°n=(n﹣2) 180°,
解得n=6,
故选:C.
2.(2025 阜平县校级一模)如图,在 ABCD中,BE⊥AB交对角线AC于点E.若∠2=130°,则∠1的度数为( )
A.30° B.40° C.45° D.50°
【解答】解:∵BE⊥AB,
∴∠ABE=90°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠1,
∵∠2=∠BAE+∠ABE,
∴∠2=∠1+∠ABE,
∴∠1+90°=130°,
∴∠1=130°﹣90°=40°,
故选:B.
3.(2025 昭阳区校级模拟)如图,在 ABCD中,∠ADC的平分线DE交BC于点E,若AB=11,BE=4,则AD的长为( )
A.15 B.11 C.20 D.52
【解答】解:∵∠ADC的平分线DE交BC于点E,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,AB=11,
∴CD=AB=11,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD=11,
∵BE=4,
∴AD=CB=CE+BE=11+4=15,
故选:A.
4.(2025 石狮市模拟)依据所标数据,下列四边形不一定为菱形的是( )
A. B.
C. D.
【解答】解:A、32+42=52,由勾股定理的逆定理推出四边形的对角线互相垂直,四边形的对角线又互相平分,判定是四边形是菱形,故A不符合题意;
B、四边形的四条边相等,判定四边形是菱形,故B不符合题意;
C、四边形的对角线互相平分,只能判定四边形是平行四边形,不能判定四边形是菱形,故C符合题意;
D、由同旁内角互补,得到四边形的两组对边平行,而四边形的邻边又相等,判定四边形是菱形,故D不符合题意.
故选:C.
5.(2025 重庆模拟)如图,在四边形ABCD中,AD∥BC,∠A=90°,AD=16,BC=21,CD=13,动点P从点B出发,沿射线BC以每秒3个单位的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位的速度向终点D运动,当动点Q到达点D时,动点P也同时停止运动.设点P的运动时间为t(秒).以点P、C、D、Q为顶点的四边形是平行四边形时t值为( )秒.
A.2或 B. C.或 D.
【解答】解:∵四边形PQDC是平行四边形,
∴DQ=CP,
当P从B运动到C时,且P在BC上,
∵DQ=AD﹣AQ=16﹣t,CP=21﹣3t,
∴16﹣t=21﹣3t,
解得t,
∴当t秒时,四边形PQDC是平行四边形;
当点P在BC延长线上时,
∴16﹣t=3t﹣21,
解得t,
∴t秒或秒时,P、Q、D、C为顶点的四边形为平行四边形.
故选:C.
6.(2025 龙泉市二模)在正方形ABCD中,AB=6,P是对角线AC上一动点,作PE⊥AD于点E,PF⊥CD于点F.若四边形PFDE的面积为6,则BP的长为( )
A.4 B. C. D.
【解答】解:∵点P是对角线AC上一动点,
∴有以下两种情况:
①当点P靠近点A时,延长EP交BC于点H,如图1所示:
∵四边形ABCD是正方形,且AB=6,
∴AB=BC=6,∠ABC=∠BCD=∠CDA=∠DAB=90°,∠DCA=45°,AD∥BC,
∴EH⊥BC,
∵PE⊥AD,PF⊥CD,
∴四边形ABHE,四边形PHCF,四边形PEDF都是矩形,
∴EH=AB=6,
∵∠DCA=45°,PF⊥CD,
∴△PCF是等腰直角三角形,
∴PF=CF,
∴矩形PFCF是正方形,
设PF=PH=CH=a,
∴PE=EH﹣PH=6﹣a,BH=BC﹣CH=6﹣a,
∵四边形PFDE的面积为6,
∴PF PE=a (6﹣a)=6,
在Rt△PBH中,由勾股定理得:BP;
②当点P靠近点C时,延长EP交BC于点H,如图2所示:
同(1)得:EH=AB=AC=6,四边形PHCF是正方形,
设PH=PF=CH=a,则BH=BC﹣CH=6﹣a,
∵四边形PFDE的面积为6,
∴PF PE=a (6﹣a)=6,
在Rt△PBH中,由勾股定理得:BP.
综上所述:BP的长为.
故选:C.
7.(2025 九龙坡区校级二模)如图,在正方形ABCD中,点E、F、G分别在AB、BC、CD上,连接AF、EG交于点H,连接CH,若CF=CG,AE=2DG,∠BAF=α,则∠HCF的度数为( )
A.45°+α B.45°﹣α C.2α D.α
【解答】解:过点D作DH∥GE交AB于点H,连接AG,FG,作△CFG的外接圆,如图所示:
∵四边形ABCD是正方形,
∴AB=DA=BC=DC,∠DAB=∠B=∠BCD=∠CDA=90°,AB∥CD,
∴四边形DHEG是平行四边形,
∴DE=HE,DH=GE,
∴AE=AH+HE=AH+DE,
∵AE=2DG,
∴AH+DE=2DG,
∴AH=DG,
在△AHD和△DGA中,
,
∴△AHD≌△DGA(SAS),
∴∠BAF=∠GAD=α,DH=AG,
∴∠FAG=∠DAB﹣(∠BAF+∠GAD)=90°﹣2α,
∵BC=DC,CF=CG,
∴BC﹣CF=DC﹣CG,
∴BF=DG,
又∵AH=DG,
∴BF=AH,
在△ABF和△DAH中,
,
∴△ABF≌△DAH(SAS),
∴∠BAF=∠ADH=α,AF=DH,
∵∠BAF+∠FAG=∠DAB=90°,
∴∠ADH+∠FAG=90°,
∴AF⊥DH,
∵DH∥GE,
∴AF⊥GE,
∴∠AGE=90°﹣∠FAG=90°﹣(90°﹣2α)=2α,
∵DH=AG,AF=DH,
∴AF=AG,
∴∠AGF=∠AFG(180°﹣∠FAG)(180°﹣90°+2α)=45°+α,
∴∠FGE=∠AGF﹣∠AGE=45°+α﹣2α=45°﹣α,
∵∠BCD=90°,
∴FG是△CFG外接圆的直径,
∵AF⊥GE,
∴∠FHG=90°,
∴点H在△CFG的外接圆上,
根据圆周角定理得:∠HCF=∠FGE=45°﹣α.
故选:B.
8.(2025 涪城区三模)如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,AD上,且AE=DF,连接BF,交DE于点G,连接GC.现有下列结论:①∠BGD=120°;②GC平分∠BGD;③CG=DG+BG;④S四边形DGBCCG2.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:连接BD,
∵四边形ABCD是菱形,
∴AD=AB=BC=CD,∠A=∠BCD,
∵∠A=60°,
∴△ABD是等边三角形,
∴∠A=∠ADB=60°,AD=BD,
在△AED和△DFB中,
,
∴△AED≌△DFB(SAS),
∴∠ADE=∠DBF,
∴∠BGE=∠BDG+∠DBF=∠BDG+∠ADE=∠ADB=60°,
∴∠BGD=180°﹣∠BGE=120°;
故①符合题意;
过C作CM⊥BG于M,CN⊥ED交ED延长线于N,则∠CNG=∠CMG=90°,
∵∠BGN=180°﹣∠BGE=120°,
∴∠MCN=360°﹣90°﹣90°﹣120°=60°,
∵∠BCD=∠A=60°,
∴∠DCN=∠BCM=60°﹣∠MCD,
在△DCN和△BCM中,
,
∴△DCN≌△BCM(AAS),
∴CN=CM,DN=BM
又∠CNG=∠CMG=90°,
CG=CG,
∴Rt△CNG≌Rt△CMG(HL),
∴∠CGN=∠CGM,
即GC平分∠BGD,
故②符合题意;
∵GC平分∠BGD,且∠BGD=120°,
∴∠NGC=∠BGC=60°
则∠GCN=∠GCM=90°﹣60°=30°,
∴,,
∵DN=BM,
则GD+GB=GD+GM+MB=GD+GM+DN=GN+GM,
即,
故③符合题意;
∴,,
∵△DCN≌△BCM(AAS),
∴S△DCN=S△BCM,
∴S四边形BCDG=S四边形MCNG=2S△CNG,
∴,
故④符合题意;
故选:D.
二.填空题(共6小题)
9.(2025 南岸区模拟)如果一个多边形的内角和是它的外角和的4倍,那么这个多边形的边数为 10 .
【解答】解:这个多边形的内角和为360°×4=1440°,
设这个多边形的边数为n,
则(n﹣2)×180°=1440°,
解得:n=10.
这个多边形的边数是10.
故答案为:10.
10.(2025 东莞市校级一模)七巧板是中国古代劳动人民发明的一种传统智力玩具,被誉为“东方魔板”,它由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成.已知图1是边长为4的大正方形,图2是小红同学将七巧板摆拼而成的“奔跑者”图案,则图2中阴影部分的面积为 6 .
【解答】解:如图1,由题意可知,四边形ABCD和四边形HKIF都是正方形,且正方形ABCD的边长为4,
∴S正方形ABCD=4×4=16,
∴S△ABD=S△CBDS正方形=8,
∵△ABI和△ADI都是等腰直角三角形,
∴S△ABIS△ABD=4,
∵△BHK、△EFI、△CHL都是等腰直角三角形,四边形HKIF是正方形,
∴IK=BK=HK=HF=LF=FI=EI=ED,
∴平行四边形EFLD、正方形HKIF、△CHL面积相等,△BHK与△EFI面积的和等于△CHL的面积,
∴S平行四边形EFLDS△CBD=2,
∵图2中的阴影部分由图1中的△ABI和平行四边形EFLD组成,
∴S阴影=4+2=6,
故答案为:6.
11.(2025 安徽模拟)正方形ABCD的对角线AC,BD交于点O,∠CAB的平分线AE交BC于点E,OB于点F.(1)∠AFD的度数为 67.5° ;
(2)的值为 .
【解答】解:(1)∵四边形ABCD是正方形,
∴∠BAC=∠DAC=∠ADB=45°,
∵AE是∠CAB的平分线,
∴∠CAE∠CAB=22.5°,
∴∠DAE=∠DAC+∠CAE=45°+22.5°=67.5°,
在△ADF中,∠AFD=180°﹣(∠DAE+∠ADB)=180°﹣(67.5°+45°)=67.5°,
故答案为:67.5°;
(2)过点F作FH⊥AB于点F,如图所示:
设FH=a,
∵四边形ABCD是正方形,
∴AB=AD,AD∥BC,AC⊥BD,OA=OB,∠ABD=45°,
∵AE是∠CAB的平分线,FH⊥AB,OF⊥AC,
∴FO=FH=a,
∵∠ABD=45°,FH⊥AB,
∴△HFB是等腰直角三角形,
∴FH=BH=a,
由勾股定理得:BF,
∴OB=FO+BF,
∴OA=OB,
在Rt△AFH和Rt△AFO中,
,
∴Rt△AFH≌Rt△AFO(HL),
∴HA=OA,
∴AD=AB=HA+BH,
由(1)可知:∠DAE=67.5°,∠AFD=67.5°,
∴∠BFE=∠AFD=67.5°,
又∵AD∥BC,
∴∠BEF=∠DAE=67.5°,
∴∠BFE=∠BEF=67.5°,
∴BE=BF,
∴.
故答案为:.
12.(2025 海南模拟)如图,已知菱形ABCD中,BD为对角线,AB=10,BD=12,点E是边AB的延长线上一点,连接DE交BC于点F,BG平分∠CBE交DE于点G.则∠DBG= 90° ,若DG=2GE,则tan∠BDG= .
【解答】解:在菱形ABCD中,BD为对角线,点E是边AB延长线上的任意一点,BG平分∠CBE交DE于点G.
∴∠CBD=∠ABD∠ABC,∠GBF=∠GBE∠EBF,
∴∠DBG=∠CBD+∠CBG(∠ABC+∠EBC)180°=90°;
连接AC交BD于点K,交DE于点L,
∵四边形ABCD是菱形,
∴AC⊥BD,CK=AK,CD∥AB,
∴∠AKB=90°,
在直角三角形ABK中,由勾股定理得:AK8,
∴CK=AK=8,
∴AC=16,
∵AC⊥BD,
∴∠DKL=∠DBG=90°,
∴AC∥BG,
∴1,
∴DL=GLDG,
∵DG=2GE,
∴GEDG,
∴DL=GL=GE,
∵CD∥AB,
∴,
∴CLAC,
∴KL=8
∴tan∠BDE.
故答案为:90°,.
13.(2025 福州模拟)图1是第九届华人数学家大会的会场背景图案,其中最具代表性的数学元素是“斐波那契螺旋线”,用以斐波那契数列“1,1,2,3,5,8,13,…(从第3个数开始,每个数是前面两个数的和)”为边的正方形拼成长方形,然后在正方形里面画90°的扇形,连起来的弧线就是斐波那契螺旋线,图2是用“1,1,2,3,5”构造的斐波那契螺旋线,它的长度为 .
【解答】解:如图所示:
∵四边形ABCD是正方形,且边长为1,
∴AB=BC=CD=AD=1,∠DAB=∠ABC=∠BCD=∠CDA=90°,
∵点C是弧DF所在圆的圆心,半径CF=1,∠DCF=90°,
∴弧DF的长度为:,
∵点B是弧FG所在圆的圆心,半径BG=2,∠FBG=90°,
∴弧FG的长度为:π,
∵点A是弧GH所在圆的圆心,半径AH=3,∠GAH=90°,
∴弧GH的长度为:,
∵点E是弧HK所在圆的圆心,半径EK=5,∠HEK=90°,
∴弧HK的长度为:,
∴图中斐波那契螺旋线长度为:.
故答案为:.
14.(2025 杭州模拟)如图,已知矩形ABCD中,点H是CD的中点,连结BD和AH交于点G,过A作BD的垂线交BD于点E,延长AE交BC于点F.若AB=BG,在BD上取一点P(不与B和D重合),使得直线CP刚好经过四边形DEFH某一条边的中点,则BP:BD的值为 或或 .
【解答】解:设CH=a,
∵H为CD中点,
∴,
∵四边形ABCD是矩形,AB=BG,
∴AD∥BC,AB∥DC,AD=BC,BG=AB=CD=2a,∠BCD=∠BAD=90°,∠BAG=∠BGA,
∵AB∥DC,∠BGA=∠DGH,
∴∠DHA=∠BAH,即∠DHG=∠BAG,
∴∠DGH=∠DHG,
∴DG=DH=a,
∴BD=BG+DG=2a+a=3a,
∵∠BAD=90°,AE⊥BD,
∴,∠AEB=90°,
又∵,
∴,
∴,
∴,
∵AD∥BC,∴∠BFE=∠DAE,∠FBE=∠ADE,
∴△EFB∽△EAD,
∴,即,
∴BFa,
∴CF=BC﹣BFaaa,
①如图,当P为DE中点时,即CP平分ED,
∴,
∴,
∴;
②如图,当CP平分EF时,设EF中点为O,过F作FN∥BD交CP于N,
∴∠PEO=∠NFO,∠EPO=∠FNO,EO=OF,
∴△OEP∽△OFN,
∴,
∴PE=NF,
∵FN∥BP,
∴∠CNF=∠CPB,∠CFN=∠CBP,
∴△CFN∽△CBP,
∴,
∴BP=5FN=5PE,
∴,
∴;
③如图,当CP平分FH时,设FH的中点为I,过P作从PN⊥BC于N,
∴∠PNC=∠BNP=∠BCD=90°,
∵∠PBN=∠DBC,
∴△BPN∽△BDC,
∴,即,
∴PNBN,
∵为EH中点,∠FCH=90°,
∴,
∴∠IFC=∠ICF,
∴,
在Rt△PNC中,,
∴,
∴BNNC,
∴2BN=5CN,
又∵,
∴,,
∴,
∴,
∴;
综上所述,BP:BD的值为,
故答案为:.
三.解答题(共7小题)
15.(2025 镇平县模拟)如图,平行四边形ABCD中,点F在AD上.
(1)请用无刻度的直尺和圆规作AE⊥BC于点E.(保留作图痕迹,不写作法);
(2)若DF=BE,连接CF,求证:四边形AECF是矩形.
【解答】(1)解:如图,AE即为所作;
(2)证明:由作图得∠AEC=90°,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,∠B=∠D,
∴∠EAD+∠AEC=180°,
∴∠EAD=90°,
在△CDF和△ABE中,
,
∴△CDF≌△ABE(SAS),
∴∠CFD=∠AEB=90°,
∴∠EAD=∠CFD=∠AEB=90°,
∴四边形AECF是矩形.
16.(2025 沛县二模)如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,过点C作CF∥AB,交DE延长线于点F,连接AF、CD.
(1)求证:四边形ADCF是菱形;
(2)当 时,四边形ADCF是正方形.
【解答】(1)证明:∵D、E分别是AB、AC中点,
∴DE是△ABC的中位线,
∴DE∥BC,
又∵CF∥AB,
∴四边形DBCF是平行四边形,
∴CF=BD,
∵D是AB的中点,
∴AD=BD,
∴CF=AD,
又∵CF∥AB,
∴四边形ADCF是平行四边形,
∵∠ACB=90°,D是AB中点,
∴.
∴CD=AD.
又∵四边形ADCF是平行四边形,
∴四边形ADCF是菱形;
(2)解:当时,四边形ADCF是正方形.
∵∠ACB=90°,
∴设ABk,AC=k,
∴BCk,
∴AC=BC,
∴△ABC是等腰直角三角形,
∵D是AB的中点,
∴CD⊥AB,
∴∠ADC=90°,
由(1)知,四边形ADCF是菱形,
∴四边形ADCF是正方形.
故答案为:.
17.(2025 道里区二模)四边形ABCD为正方形,点E,F分别在BC,CD上,连接BF,DE,∠ADE=∠ABF.
(1)如图1,求证:DE=BF;
(2)如图2,设BF与DE交于点G,∠ABF=2∠CBF,在不添加任何辅助线的情况下,请写出图中所有等于的线段.
【解答】(1)证明:∵四边形ABCD为正方形,
∴AB=AD=DC=BC,∠ADC=∠ABC=∠C=90°,
∵∠ADE=∠ABF,
∴∠ADC﹣∠ADE=∠ABC﹣∠ABF,
∴∠CDE=∠CBF,
在△CDE和△CBF中,
,
∴△CDE≌△CBF(ASA),
∴DE=BF;
(2)图中等于ABDE的线段有:BE,GE,GF,DF四条,理由如下:
∵∠ABF=2∠CBF,
又∵∠ABC=∠ABF+∠CBF=90°,
∴2∠CBF+∠CBF=90°,
∴∠CBF=30°,
∴∠ABF=2∠CBF=60°,
∵∠ADE=∠ABF,
∴∠CDE=∠CBF=30°,
在Rt△DEC中,∠DEC=90°﹣∠CDE=60°,
∵∠DEC是△EBG的外角,
∴∠DEC=∠CBF+∠EGB,
∴60°=30°+∠EGB,
∴∠EGB=∠CBF=30°,
∴BE=GE,
同理:GF=DF,
由(1)可知:△CDE≌△CBF,
∴CE=CF,
∵BC=DC,
∴BC﹣CE=DC﹣CF,
∴BE=DF,
∴BE=GE=GF=DF,
设CF=a,
∴CE=CF=a,
在Rt△CBF中,∠CBF=30°,
∴BF=2CF=2a,
由(1)可知:DE=BF=2a,
由勾股定理得:BC,
∴AB=BC,BE=BC﹣CE,
∵ABDE,
∴ABDE=BE,
∴线段BE,GE,GF,DF的长都等于ABDE.
18.(2025 儋州模拟)已知正方形ABCD,一等腰直角三角形EFG的斜边EG经过其顶点B,直角边GF所在直线经过其顶点A(点B不与E,G重合,点A不与F,G重合),∠EFG=90°,EF=FG=6,,连接CG.
(1)如图1,若点B为EG的中点,且边GF的延长线经过顶点A时,连接BF.求∠BGC的度数.
(2)如图2,若顶点B不是EG中点,且顶点A在边FG上时,作CM⊥EG于点M,BE,.
①求∠BGC的度数;
②连接AC,交BG于点P,求CP的长.
【解答】解:(1)∵∠EFG=90°,FE=FG,B为EG的中点,
∴BF=BG,∠FBG=90°,∠BFG=45°,
∴∠AFB=135°,
∵四边形ABCD为正方形,
∴∠ABC=90°,BA=BC,
∴∠ABC﹣∠FBC=∠FBG﹣∠FBC,
即∠ABF=∠CBG.
在△ABF和△CBG中,
,
∴△ABF≌△CBG(SAS).
∴∠BGC=∠AFB=135°.
(2)①∵∠EFG=90°,FE=FG=6,
∴EG=6.
∵BE=2,,
∴,
∴.
∵CM⊥EG,∠BMC=∠GMC=90°.
∵,BM,
∴CM3,
∴CM=MG,∠MGC=45°,
即∠BGC=45°;
②如图:
∵∠BGC=45°,∠BGA=45°,∠BAC=45°,
∴∠CPG=∠AGP+∠PAG=45°+∠PAG,∠BAG=∠BAC+∠PAG=45°+∠PAG,
∴∠BAG=∠CPG.
又∵∠AGB=∠PGC,
∴△AGB∽△PGC,
∴.
∵,
∴.
∵,CM⊥EG,
∴,
∴,
∴.
19.(2025 泌阳县二模)在学习特殊四边形的过程中,我们对四边形有一些了解,并积累了一定的研究经验.定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.请运用已有经验,对“邻等对补四边形”进行研究.
(1)概念理解
①在以下四种图形中,一定是邻等对补四边形的是 D ;
A.平行四边形
B.菱形
C.矩形
D.正方形
②分别用含有30°和45°角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有 ②④ .(填序号)
(2)概念应用
如图2,∠BAD=60°,且AB=AD.请你用尺规作图在平面内找出动点C的轨迹,使得四边形ABCD总是邻等对补四边形.(保留作图痕迹,不写作法)
(3)综合探究
在(2)的基础上,连接AC,探究线段AC,BC,CD之间满足的数量关系.
【解答】解:(1)根据“邻等对补四边形”的定义,正方形一定是“邻等对补四边形”.
故答案为:D.
②“邻等对补四边形”是②④.
故答案为:②④;
(2)如图,点C在上移动(不与B,D重合)时,四边形ABCD总是邻等对补四边形.
(3)AC=CD+BC.理由如下:如图,延长BC至点E,使得CE=CD,连接ED,DB.
∵AB=AD,∠BAD=60°,
∴△ABD是等边三角形.
∴BD=AD,∠BDA=60°,
∵四边形ABCD是邻等对补四边形,
∴∠BCD=180°﹣∠BAD=120°.
∴∠ECD=60°,
∴△ECD 是等边三角形.
∴ED=CD,∠EDC=60°,
∴∠EDC+∠CDB=∠CDB+∠BDA.
∴∠EDB=∠CDA.
∴△EBD≌△CAD(SAS).
∴AC=EB=EC+CB=CD+BC.
20.(2025 安州区三模)如图,在△ABC中,AC=5,CD为AB边上的高,且CD=BD,tan∠CAB,E,M为AC边上两个不重合的动点(点E在点M的上方,且均不与端点重合),EF∥AB,与边BC交于点F,四边形EMNF为平行四边形,连接BN.
(1)求AD,BD的长.
(2)如图①,若四边形EMNF为菱形,点N在CD上,当tan∠ABN时,求该菱形的边长.
(3)如图②,若BF=BN,则当EF长为多少时,平行四边形EMNF的面积取得最大值?求出最大值.
【解答】解:(1)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∵tan∠CAB,
∴设CD=4x,AD=3x,
∴AC5x=5,
∴x=1,
∴AD=3,CD=4,
∴BD=CD=4;
(2)如图,过点E作EH⊥MN于点H,设EF与CD交于点R,过点M作MG⊥AB于点G,过点N作NK⊥AB于点K.
∵EF∥AB,四边形EMNF为菱形,CD=BD,
∴tan∠CAD=tan∠CER,
∴,即,
设RF=x,则,
∴,
∵四边形EMNF为菱形,
∴,
在Rt△EMH中,,
∴,
∴,
∴,
∴,
∴.
∵,
∴BK=2NK.,
∴.
∵BK=2KN,
∴,
解得,
∴,
∴当时,菱形EMNF 的边长为.
(3)如图,过点B作BP⊥AC于点P,与NF交于点Q,过点E作ET⊥MN于点T.设CD与EF交于点W.
在Rt△ABP中,∠APB=90°AB=3+4=7.
∵,
∴设PB=4a,AP=3a,
∴(4a)2+(3a)2=72,
∴或舍去),
∴,
∴,
当BN=BF时,△BNF是等腰三角形.
∵BP⊥AC,NF∥AC,
∴BQ⊥NF,
∴BQ为△BNF 的中线和高,即NF=2QF.
设WF=m,则,
∴BF=BC﹣CF=42﹣2m,
∵NF∥AC,
∴,即,
解得,
∴ME,
在Rt△EMT中,,
∴,
∴,
同(2)可得EF,S四边形EMNF=EF,
当m=2时,,
∴当EF时,平行四边形EMNF的面积有最大值,最大值为.
21.(2025 姑苏区校级二模)实践探究:两位同学利用菱形纸片进行翻折问题的自主探究,已知纸片为菱形ABCD,其边长为4,一个内角∠A=60°.
(1)如图1,他们将△AMN沿直线MN翻折得到△EMN,使得点E正好落在边CD上,且EM⊥AB,两位同学发现了不同的解法来求出图中线段DN的长度,一位同学找到了图中的一个特殊的等腰三角形,另一位同学则利用轴对称图形对应边相等这一性质;请聪明的你利用提示来求出线段DN的长度;
(2)如图2,两位同学又将△APQ沿直线PQ翻折得到△FPQ,使得点F正好是边CD的中点,那么此时线段DQ的长度是多少呢?
(3)如图3,点G为BC边上一点,将△ABG沿直线AG翻折得到△AKG,BK,AK的延长线分别交CD于S,T两点,若,求线段ST的长度.
【解答】解:(1)法一(利用特殊等腰三角形):
∵菱形ABCD边长为4,∠A=60°,EM⊥AB,
故EM=sin60° AB.
由折叠可知AM=EM,
设AP=x,则PMx,
作NP⊥AB于点P,由EM⊥AB及折叠可知∠EMN=∠PMN=45°,如图1所示,
∴∠PNM=45°,∠ANP=30°,PN=PM,
∴PN,
即x,解得x,
此时AN=2AP,
故DN=AD﹣AN=4﹣().
法二(利用轴对称性质):如图1所示,延长PN交CD延长线于点Q,则PQ⊥CD.
设DN=x,由折叠性质可得AN=4﹣x=NE,
∵∠ANP=∠QND=30°,
∴QN=cos30° DN,
又∵∠QEN=90°﹣∠NEM=90°﹣60°=30°,
∴QN,
故,解得x.
即DN的长度为.
(2)过点Q作MN⊥AB于点N,交CD延长线于点M,如图2所示,
由(1)知MN,
设DQ=x,则AQ=4﹣x=QF,
∵∠MQD=∠MFQ=30°,
∴QM,DM,
在Rt△MQF中,由勾股定理可得 MQ2+MF2=QF2,
即,解得x.
即DQ长为.
(3)由折叠可知AK=AB=4,∠ABK=∠AKB=∠SKT,
∵DC∥AB,
∴∠KST=∠ABK,
故ST=KT.
延长AG交DC的延长线于点R,作AH⊥CD的延长线于点H,如图3所示,
则CG=CB﹣BG=4,
∵CR∥AB,
∴△CRG∽△BAG,
∴,故CR6,
∵CR∥AB,
∴∠R=∠RAB=∠KAR,
∴AT=RT,
设ST=KT=x,则AT=4+x=RT,
∴TC=RT﹣CR=4+x﹣6=x﹣2,
故DS=DC﹣SC=4﹣(2x﹣2)=6﹣2x,
∵∠HAD=30°,
∴DH2,AH=HT=DH+DT=2+6﹣x=8﹣x,
在Rt△AHT中,由勾股定理可得,
解得x,
故ST长为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【中考模拟题汇编】查漏补缺:四边形-2025年中考数学
一.选择题(共8小题)
1.(2025 中山区一模)若正多边形的一个内角是120°,则这个正多边形的边数为( )
A.8 B.7 C.6 D.5
2.(2025 阜平县校级一模)如图,在 ABCD中,BE⊥AB交对角线AC于点E.若∠2=130°,则∠1的度数为( )
A.30° B.40° C.45° D.50°
3.(2025 昭阳区校级模拟)如图,在 ABCD中,∠ADC的平分线DE交BC于点E,若AB=11,BE=4,则AD的长为( )
A.15 B.11 C.20 D.52
4.(2025 石狮市模拟)依据所标数据,下列四边形不一定为菱形的是( )
A. B.
C. D.
5.(2025 重庆模拟)如图,在四边形ABCD中,AD∥BC,∠A=90°,AD=16,BC=21,CD=13,动点P从点B出发,沿射线BC以每秒3个单位的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位的速度向终点D运动,当动点Q到达点D时,动点P也同时停止运动.设点P的运动时间为t(秒).以点P、C、D、Q为顶点的四边形是平行四边形时t值为( )秒.
A.2或 B. C.或 D.
6.(2025 龙泉市二模)在正方形ABCD中,AB=6,P是对角线AC上一动点,作PE⊥AD于点E,PF⊥CD于点F.若四边形PFDE的面积为6,则BP的长为( )
A.4 B. C. D.
7.(2025 九龙坡区校级二模)如图,在正方形ABCD中,点E、F、G分别在AB、BC、CD上,连接AF、EG交于点H,连接CH,若CF=CG,AE=2DG,∠BAF=α,则∠HCF的度数为( )
A.45°+α B.45°﹣α C.2α D.α
8.(2025 涪城区三模)如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,AD上,且AE=DF,连接BF,交DE于点G,连接GC.现有下列结论:①∠BGD=120°;②GC平分∠BGD;③CG=DG+BG;④S四边形DGBCCG2.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题)
9.(2025 南岸区模拟)如果一个多边形的内角和是它的外角和的4倍,那么这个多边形的边数为 .
10.(2025 东莞市校级一模)七巧板是中国古代劳动人民发明的一种传统智力玩具,被誉为“东方魔板”,它由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成.已知图1是边长为4的大正方形,图2是小红同学将七巧板摆拼而成的“奔跑者”图案,则图2中阴影部分的面积为 .
11.(2025 安徽模拟)正方形ABCD的对角线AC,BD交于点O,∠CAB的平分线AE交BC于点E,OB于点F.(1)∠AFD的度数为 ;
(2)的值为 .
12.(2025 海南模拟)如图,已知菱形ABCD中,BD为对角线,AB=10,BD=12,点E是边AB的延长线上一点,连接DE交BC于点F,BG平分∠CBE交DE于点G.则∠DBG= ,若DG=2GE,则tan∠BDG= .
13.(2025 福州模拟)图1是第九届华人数学家大会的会场背景图案,其中最具代表性的数学元素是“斐波那契螺旋线”,用以斐波那契数列“1,1,2,3,5,8,13,…(从第3个数开始,每个数是前面两个数的和)”为边的正方形拼成长方形,然后在正方形里面画90°的扇形,连起来的弧线就是斐波那契螺旋线,图2是用“1,1,2,3,5”构造的斐波那契螺旋线,它的长度为 .
14.(2025 杭州模拟)如图,已知矩形ABCD中,点H是CD的中点,连结BD和AH交于点G,过A作BD的垂线交BD于点E,延长AE交BC于点F.若AB=BG,在BD上取一点P(不与B和D重合),使得直线CP刚好经过四边形DEFH某一条边的中点,则BP:BD的值为 .
三.解答题(共7小题)
15.(2025 镇平县模拟)如图,平行四边形ABCD中,点F在AD上.
(1)请用无刻度的直尺和圆规作AE⊥BC于点E.(保留作图痕迹,不写作法);
(2)若DF=BE,连接CF,求证:四边形AECF是矩形.
16.(2025 沛县二模)如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,过点C作CF∥AB,交DE延长线于点F,连接AF、CD.
(1)求证:四边形ADCF是菱形;
(2)当 时,四边形ADCF是正方形.
17.(2025 道里区二模)四边形ABCD为正方形,点E,F分别在BC,CD上,连接BF,DE,∠ADE=∠ABF.
(1)如图1,求证:DE=BF;
(2)如图2,设BF与DE交于点G,∠ABF=2∠CBF,在不添加任何辅助线的情况下,请写出图中所有等于的线段.
18.(2025 儋州模拟)已知正方形ABCD,一等腰直角三角形EFG的斜边EG经过其顶点B,直角边GF所在直线经过其顶点A(点B不与E,G重合,点A不与F,G重合),∠EFG=90°,EF=FG=6,,连接CG.
(1)如图1,若点B为EG的中点,且边GF的延长线经过顶点A时,连接BF.求∠BGC的度数.
(2)如图2,若顶点B不是EG中点,且顶点A在边FG上时,作CM⊥EG于点M,BE,.
①求∠BGC的度数;
②连接AC,交BG于点P,求CP的长.
19.(2025 泌阳县二模)在学习特殊四边形的过程中,我们对四边形有一些了解,并积累了一定的研究经验.定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.请运用已有经验,对“邻等对补四边形”进行研究.
(1)概念理解
①在以下四种图形中,一定是邻等对补四边形的是 ;
A.平行四边形
B.菱形
C.矩形
D.正方形
②分别用含有30°和45°角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有 .(填序号)
(2)概念应用
如图2,∠BAD=60°,且AB=AD.请你用尺规作图在平面内找出动点C的轨迹,使得四边形ABCD总是邻等对补四边形.(保留作图痕迹,不写作法)
(3)综合探究
在(2)的基础上,连接AC,探究线段AC,BC,CD之间满足的数量关系.
20.(2025 安州区三模)如图,在△ABC中,AC=5,CD为AB边上的高,且CD=BD,tan∠CAB,E,M为AC边上两个不重合的动点(点E在点M的上方,且均不与端点重合),EF∥AB,与边BC交于点F,四边形EMNF为平行四边形,连接BN.
(1)求AD,BD的长.
(2)如图①,若四边形EMNF为菱形,点N在CD上,当tan∠ABN时,求该菱形的边长.
(3)如图②,若BF=BN,则当EF长为多少时,平行四边形EMNF的面积取得最大值?求出最大值.
21.(2025 姑苏区校级二模)实践探究:两位同学利用菱形纸片进行翻折问题的自主探究,已知纸片为菱形ABCD,其边长为4,一个内角∠A=60°.
(1)如图1,他们将△AMN沿直线MN翻折得到△EMN,使得点E正好落在边CD上,且EM⊥AB,两位同学发现了不同的解法来求出图中线段DN的长度,一位同学找到了图中的一个特殊的等腰三角形,另一位同学则利用轴对称图形对应边相等这一性质;请聪明的你利用提示来求出线段DN的长度;
(2)如图2,两位同学又将△APQ沿直线PQ翻折得到△FPQ,使得点F正好是边CD的中点,那么此时线段DQ的长度是多少呢?
(3)如图3,点G为BC边上一点,将△ABG沿直线AG翻折得到△AKG,BK,AK的延长线分别交CD于S,T两点,若,求线段ST的长度.
【中考模拟题汇编】查漏补缺:四边形-2025年中考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C B A C C C B D
一.选择题(共8小题)
1.(2025 中山区一模)若正多边形的一个内角是120°,则这个正多边形的边数为( )
A.8 B.7 C.6 D.5
【解答】解:设所求正n边形边数为n,
则120°n=(n﹣2) 180°,
解得n=6,
故选:C.
2.(2025 阜平县校级一模)如图,在 ABCD中,BE⊥AB交对角线AC于点E.若∠2=130°,则∠1的度数为( )
A.30° B.40° C.45° D.50°
【解答】解:∵BE⊥AB,
∴∠ABE=90°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠1,
∵∠2=∠BAE+∠ABE,
∴∠2=∠1+∠ABE,
∴∠1+90°=130°,
∴∠1=130°﹣90°=40°,
故选:B.
3.(2025 昭阳区校级模拟)如图,在 ABCD中,∠ADC的平分线DE交BC于点E,若AB=11,BE=4,则AD的长为( )
A.15 B.11 C.20 D.52
【解答】解:∵∠ADC的平分线DE交BC于点E,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,AB=11,
∴CD=AB=11,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD=11,
∵BE=4,
∴AD=CB=CE+BE=11+4=15,
故选:A.
4.(2025 石狮市模拟)依据所标数据,下列四边形不一定为菱形的是( )
A. B.
C. D.
【解答】解:A、32+42=52,由勾股定理的逆定理推出四边形的对角线互相垂直,四边形的对角线又互相平分,判定是四边形是菱形,故A不符合题意;
B、四边形的四条边相等,判定四边形是菱形,故B不符合题意;
C、四边形的对角线互相平分,只能判定四边形是平行四边形,不能判定四边形是菱形,故C符合题意;
D、由同旁内角互补,得到四边形的两组对边平行,而四边形的邻边又相等,判定四边形是菱形,故D不符合题意.
故选:C.
5.(2025 重庆模拟)如图,在四边形ABCD中,AD∥BC,∠A=90°,AD=16,BC=21,CD=13,动点P从点B出发,沿射线BC以每秒3个单位的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位的速度向终点D运动,当动点Q到达点D时,动点P也同时停止运动.设点P的运动时间为t(秒).以点P、C、D、Q为顶点的四边形是平行四边形时t值为( )秒.
A.2或 B. C.或 D.
【解答】解:∵四边形PQDC是平行四边形,
∴DQ=CP,
当P从B运动到C时,且P在BC上,
∵DQ=AD﹣AQ=16﹣t,CP=21﹣3t,
∴16﹣t=21﹣3t,
解得t,
∴当t秒时,四边形PQDC是平行四边形;
当点P在BC延长线上时,
∴16﹣t=3t﹣21,
解得t,
∴t秒或秒时,P、Q、D、C为顶点的四边形为平行四边形.
故选:C.
6.(2025 龙泉市二模)在正方形ABCD中,AB=6,P是对角线AC上一动点,作PE⊥AD于点E,PF⊥CD于点F.若四边形PFDE的面积为6,则BP的长为( )
A.4 B. C. D.
【解答】解:∵点P是对角线AC上一动点,
∴有以下两种情况:
①当点P靠近点A时,延长EP交BC于点H,如图1所示:
∵四边形ABCD是正方形,且AB=6,
∴AB=BC=6,∠ABC=∠BCD=∠CDA=∠DAB=90°,∠DCA=45°,AD∥BC,
∴EH⊥BC,
∵PE⊥AD,PF⊥CD,
∴四边形ABHE,四边形PHCF,四边形PEDF都是矩形,
∴EH=AB=6,
∵∠DCA=45°,PF⊥CD,
∴△PCF是等腰直角三角形,
∴PF=CF,
∴矩形PFCF是正方形,
设PF=PH=CH=a,
∴PE=EH﹣PH=6﹣a,BH=BC﹣CH=6﹣a,
∵四边形PFDE的面积为6,
∴PF PE=a (6﹣a)=6,
在Rt△PBH中,由勾股定理得:BP;
②当点P靠近点C时,延长EP交BC于点H,如图2所示:
同(1)得:EH=AB=AC=6,四边形PHCF是正方形,
设PH=PF=CH=a,则BH=BC﹣CH=6﹣a,
∵四边形PFDE的面积为6,
∴PF PE=a (6﹣a)=6,
在Rt△PBH中,由勾股定理得:BP.
综上所述:BP的长为.
故选:C.
7.(2025 九龙坡区校级二模)如图,在正方形ABCD中,点E、F、G分别在AB、BC、CD上,连接AF、EG交于点H,连接CH,若CF=CG,AE=2DG,∠BAF=α,则∠HCF的度数为( )
A.45°+α B.45°﹣α C.2α D.α
【解答】解:过点D作DH∥GE交AB于点H,连接AG,FG,作△CFG的外接圆,如图所示:
∵四边形ABCD是正方形,
∴AB=DA=BC=DC,∠DAB=∠B=∠BCD=∠CDA=90°,AB∥CD,
∴四边形DHEG是平行四边形,
∴DE=HE,DH=GE,
∴AE=AH+HE=AH+DE,
∵AE=2DG,
∴AH+DE=2DG,
∴AH=DG,
在△AHD和△DGA中,
,
∴△AHD≌△DGA(SAS),
∴∠BAF=∠GAD=α,DH=AG,
∴∠FAG=∠DAB﹣(∠BAF+∠GAD)=90°﹣2α,
∵BC=DC,CF=CG,
∴BC﹣CF=DC﹣CG,
∴BF=DG,
又∵AH=DG,
∴BF=AH,
在△ABF和△DAH中,
,
∴△ABF≌△DAH(SAS),
∴∠BAF=∠ADH=α,AF=DH,
∵∠BAF+∠FAG=∠DAB=90°,
∴∠ADH+∠FAG=90°,
∴AF⊥DH,
∵DH∥GE,
∴AF⊥GE,
∴∠AGE=90°﹣∠FAG=90°﹣(90°﹣2α)=2α,
∵DH=AG,AF=DH,
∴AF=AG,
∴∠AGF=∠AFG(180°﹣∠FAG)(180°﹣90°+2α)=45°+α,
∴∠FGE=∠AGF﹣∠AGE=45°+α﹣2α=45°﹣α,
∵∠BCD=90°,
∴FG是△CFG外接圆的直径,
∵AF⊥GE,
∴∠FHG=90°,
∴点H在△CFG的外接圆上,
根据圆周角定理得:∠HCF=∠FGE=45°﹣α.
故选:B.
8.(2025 涪城区三模)如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,AD上,且AE=DF,连接BF,交DE于点G,连接GC.现有下列结论:①∠BGD=120°;②GC平分∠BGD;③CG=DG+BG;④S四边形DGBCCG2.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:连接BD,
∵四边形ABCD是菱形,
∴AD=AB=BC=CD,∠A=∠BCD,
∵∠A=60°,
∴△ABD是等边三角形,
∴∠A=∠ADB=60°,AD=BD,
在△AED和△DFB中,
,
∴△AED≌△DFB(SAS),
∴∠ADE=∠DBF,
∴∠BGE=∠BDG+∠DBF=∠BDG+∠ADE=∠ADB=60°,
∴∠BGD=180°﹣∠BGE=120°;
故①符合题意;
过C作CM⊥BG于M,CN⊥ED交ED延长线于N,则∠CNG=∠CMG=90°,
∵∠BGN=180°﹣∠BGE=120°,
∴∠MCN=360°﹣90°﹣90°﹣120°=60°,
∵∠BCD=∠A=60°,
∴∠DCN=∠BCM=60°﹣∠MCD,
在△DCN和△BCM中,
,
∴△DCN≌△BCM(AAS),
∴CN=CM,DN=BM
又∠CNG=∠CMG=90°,
CG=CG,
∴Rt△CNG≌Rt△CMG(HL),
∴∠CGN=∠CGM,
即GC平分∠BGD,
故②符合题意;
∵GC平分∠BGD,且∠BGD=120°,
∴∠NGC=∠BGC=60°
则∠GCN=∠GCM=90°﹣60°=30°,
∴,,
∵DN=BM,
则GD+GB=GD+GM+MB=GD+GM+DN=GN+GM,
即,
故③符合题意;
∴,,
∵△DCN≌△BCM(AAS),
∴S△DCN=S△BCM,
∴S四边形BCDG=S四边形MCNG=2S△CNG,
∴,
故④符合题意;
故选:D.
二.填空题(共6小题)
9.(2025 南岸区模拟)如果一个多边形的内角和是它的外角和的4倍,那么这个多边形的边数为 10 .
【解答】解:这个多边形的内角和为360°×4=1440°,
设这个多边形的边数为n,
则(n﹣2)×180°=1440°,
解得:n=10.
这个多边形的边数是10.
故答案为:10.
10.(2025 东莞市校级一模)七巧板是中国古代劳动人民发明的一种传统智力玩具,被誉为“东方魔板”,它由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成.已知图1是边长为4的大正方形,图2是小红同学将七巧板摆拼而成的“奔跑者”图案,则图2中阴影部分的面积为 6 .
【解答】解:如图1,由题意可知,四边形ABCD和四边形HKIF都是正方形,且正方形ABCD的边长为4,
∴S正方形ABCD=4×4=16,
∴S△ABD=S△CBDS正方形=8,
∵△ABI和△ADI都是等腰直角三角形,
∴S△ABIS△ABD=4,
∵△BHK、△EFI、△CHL都是等腰直角三角形,四边形HKIF是正方形,
∴IK=BK=HK=HF=LF=FI=EI=ED,
∴平行四边形EFLD、正方形HKIF、△CHL面积相等,△BHK与△EFI面积的和等于△CHL的面积,
∴S平行四边形EFLDS△CBD=2,
∵图2中的阴影部分由图1中的△ABI和平行四边形EFLD组成,
∴S阴影=4+2=6,
故答案为:6.
11.(2025 安徽模拟)正方形ABCD的对角线AC,BD交于点O,∠CAB的平分线AE交BC于点E,OB于点F.(1)∠AFD的度数为 67.5° ;
(2)的值为 .
【解答】解:(1)∵四边形ABCD是正方形,
∴∠BAC=∠DAC=∠ADB=45°,
∵AE是∠CAB的平分线,
∴∠CAE∠CAB=22.5°,
∴∠DAE=∠DAC+∠CAE=45°+22.5°=67.5°,
在△ADF中,∠AFD=180°﹣(∠DAE+∠ADB)=180°﹣(67.5°+45°)=67.5°,
故答案为:67.5°;
(2)过点F作FH⊥AB于点F,如图所示:
设FH=a,
∵四边形ABCD是正方形,
∴AB=AD,AD∥BC,AC⊥BD,OA=OB,∠ABD=45°,
∵AE是∠CAB的平分线,FH⊥AB,OF⊥AC,
∴FO=FH=a,
∵∠ABD=45°,FH⊥AB,
∴△HFB是等腰直角三角形,
∴FH=BH=a,
由勾股定理得:BF,
∴OB=FO+BF,
∴OA=OB,
在Rt△AFH和Rt△AFO中,
,
∴Rt△AFH≌Rt△AFO(HL),
∴HA=OA,
∴AD=AB=HA+BH,
由(1)可知:∠DAE=67.5°,∠AFD=67.5°,
∴∠BFE=∠AFD=67.5°,
又∵AD∥BC,
∴∠BEF=∠DAE=67.5°,
∴∠BFE=∠BEF=67.5°,
∴BE=BF,
∴.
故答案为:.
12.(2025 海南模拟)如图,已知菱形ABCD中,BD为对角线,AB=10,BD=12,点E是边AB的延长线上一点,连接DE交BC于点F,BG平分∠CBE交DE于点G.则∠DBG= 90° ,若DG=2GE,则tan∠BDG= .
【解答】解:在菱形ABCD中,BD为对角线,点E是边AB延长线上的任意一点,BG平分∠CBE交DE于点G.
∴∠CBD=∠ABD∠ABC,∠GBF=∠GBE∠EBF,
∴∠DBG=∠CBD+∠CBG(∠ABC+∠EBC)180°=90°;
连接AC交BD于点K,交DE于点L,
∵四边形ABCD是菱形,
∴AC⊥BD,CK=AK,CD∥AB,
∴∠AKB=90°,
在直角三角形ABK中,由勾股定理得:AK8,
∴CK=AK=8,
∴AC=16,
∵AC⊥BD,
∴∠DKL=∠DBG=90°,
∴AC∥BG,
∴1,
∴DL=GLDG,
∵DG=2GE,
∴GEDG,
∴DL=GL=GE,
∵CD∥AB,
∴,
∴CLAC,
∴KL=8
∴tan∠BDE.
故答案为:90°,.
13.(2025 福州模拟)图1是第九届华人数学家大会的会场背景图案,其中最具代表性的数学元素是“斐波那契螺旋线”,用以斐波那契数列“1,1,2,3,5,8,13,…(从第3个数开始,每个数是前面两个数的和)”为边的正方形拼成长方形,然后在正方形里面画90°的扇形,连起来的弧线就是斐波那契螺旋线,图2是用“1,1,2,3,5”构造的斐波那契螺旋线,它的长度为 .
【解答】解:如图所示:
∵四边形ABCD是正方形,且边长为1,
∴AB=BC=CD=AD=1,∠DAB=∠ABC=∠BCD=∠CDA=90°,
∵点C是弧DF所在圆的圆心,半径CF=1,∠DCF=90°,
∴弧DF的长度为:,
∵点B是弧FG所在圆的圆心,半径BG=2,∠FBG=90°,
∴弧FG的长度为:π,
∵点A是弧GH所在圆的圆心,半径AH=3,∠GAH=90°,
∴弧GH的长度为:,
∵点E是弧HK所在圆的圆心,半径EK=5,∠HEK=90°,
∴弧HK的长度为:,
∴图中斐波那契螺旋线长度为:.
故答案为:.
14.(2025 杭州模拟)如图,已知矩形ABCD中,点H是CD的中点,连结BD和AH交于点G,过A作BD的垂线交BD于点E,延长AE交BC于点F.若AB=BG,在BD上取一点P(不与B和D重合),使得直线CP刚好经过四边形DEFH某一条边的中点,则BP:BD的值为 或或 .
【解答】解:设CH=a,
∵H为CD中点,
∴,
∵四边形ABCD是矩形,AB=BG,
∴AD∥BC,AB∥DC,AD=BC,BG=AB=CD=2a,∠BCD=∠BAD=90°,∠BAG=∠BGA,
∵AB∥DC,∠BGA=∠DGH,
∴∠DHA=∠BAH,即∠DHG=∠BAG,
∴∠DGH=∠DHG,
∴DG=DH=a,
∴BD=BG+DG=2a+a=3a,
∵∠BAD=90°,AE⊥BD,
∴,∠AEB=90°,
又∵,
∴,
∴,
∴,
∵AD∥BC,∴∠BFE=∠DAE,∠FBE=∠ADE,
∴△EFB∽△EAD,
∴,即,
∴BFa,
∴CF=BC﹣BFaaa,
①如图,当P为DE中点时,即CP平分ED,
∴,
∴,
∴;
②如图,当CP平分EF时,设EF中点为O,过F作FN∥BD交CP于N,
∴∠PEO=∠NFO,∠EPO=∠FNO,EO=OF,
∴△OEP∽△OFN,
∴,
∴PE=NF,
∵FN∥BP,
∴∠CNF=∠CPB,∠CFN=∠CBP,
∴△CFN∽△CBP,
∴,
∴BP=5FN=5PE,
∴,
∴;
③如图,当CP平分FH时,设FH的中点为I,过P作从PN⊥BC于N,
∴∠PNC=∠BNP=∠BCD=90°,
∵∠PBN=∠DBC,
∴△BPN∽△BDC,
∴,即,
∴PNBN,
∵为EH中点,∠FCH=90°,
∴,
∴∠IFC=∠ICF,
∴,
在Rt△PNC中,,
∴,
∴BNNC,
∴2BN=5CN,
又∵,
∴,,
∴,
∴,
∴;
综上所述,BP:BD的值为,
故答案为:.
三.解答题(共7小题)
15.(2025 镇平县模拟)如图,平行四边形ABCD中,点F在AD上.
(1)请用无刻度的直尺和圆规作AE⊥BC于点E.(保留作图痕迹,不写作法);
(2)若DF=BE,连接CF,求证:四边形AECF是矩形.
【解答】(1)解:如图,AE即为所作;
(2)证明:由作图得∠AEC=90°,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,∠B=∠D,
∴∠EAD+∠AEC=180°,
∴∠EAD=90°,
在△CDF和△ABE中,
,
∴△CDF≌△ABE(SAS),
∴∠CFD=∠AEB=90°,
∴∠EAD=∠CFD=∠AEB=90°,
∴四边形AECF是矩形.
16.(2025 沛县二模)如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,过点C作CF∥AB,交DE延长线于点F,连接AF、CD.
(1)求证:四边形ADCF是菱形;
(2)当 时,四边形ADCF是正方形.
【解答】(1)证明:∵D、E分别是AB、AC中点,
∴DE是△ABC的中位线,
∴DE∥BC,
又∵CF∥AB,
∴四边形DBCF是平行四边形,
∴CF=BD,
∵D是AB的中点,
∴AD=BD,
∴CF=AD,
又∵CF∥AB,
∴四边形ADCF是平行四边形,
∵∠ACB=90°,D是AB中点,
∴.
∴CD=AD.
又∵四边形ADCF是平行四边形,
∴四边形ADCF是菱形;
(2)解:当时,四边形ADCF是正方形.
∵∠ACB=90°,
∴设ABk,AC=k,
∴BCk,
∴AC=BC,
∴△ABC是等腰直角三角形,
∵D是AB的中点,
∴CD⊥AB,
∴∠ADC=90°,
由(1)知,四边形ADCF是菱形,
∴四边形ADCF是正方形.
故答案为:.
17.(2025 道里区二模)四边形ABCD为正方形,点E,F分别在BC,CD上,连接BF,DE,∠ADE=∠ABF.
(1)如图1,求证:DE=BF;
(2)如图2,设BF与DE交于点G,∠ABF=2∠CBF,在不添加任何辅助线的情况下,请写出图中所有等于的线段.
【解答】(1)证明:∵四边形ABCD为正方形,
∴AB=AD=DC=BC,∠ADC=∠ABC=∠C=90°,
∵∠ADE=∠ABF,
∴∠ADC﹣∠ADE=∠ABC﹣∠ABF,
∴∠CDE=∠CBF,
在△CDE和△CBF中,
,
∴△CDE≌△CBF(ASA),
∴DE=BF;
(2)图中等于ABDE的线段有:BE,GE,GF,DF四条,理由如下:
∵∠ABF=2∠CBF,
又∵∠ABC=∠ABF+∠CBF=90°,
∴2∠CBF+∠CBF=90°,
∴∠CBF=30°,
∴∠ABF=2∠CBF=60°,
∵∠ADE=∠ABF,
∴∠CDE=∠CBF=30°,
在Rt△DEC中,∠DEC=90°﹣∠CDE=60°,
∵∠DEC是△EBG的外角,
∴∠DEC=∠CBF+∠EGB,
∴60°=30°+∠EGB,
∴∠EGB=∠CBF=30°,
∴BE=GE,
同理:GF=DF,
由(1)可知:△CDE≌△CBF,
∴CE=CF,
∵BC=DC,
∴BC﹣CE=DC﹣CF,
∴BE=DF,
∴BE=GE=GF=DF,
设CF=a,
∴CE=CF=a,
在Rt△CBF中,∠CBF=30°,
∴BF=2CF=2a,
由(1)可知:DE=BF=2a,
由勾股定理得:BC,
∴AB=BC,BE=BC﹣CE,
∵ABDE,
∴ABDE=BE,
∴线段BE,GE,GF,DF的长都等于ABDE.
18.(2025 儋州模拟)已知正方形ABCD,一等腰直角三角形EFG的斜边EG经过其顶点B,直角边GF所在直线经过其顶点A(点B不与E,G重合,点A不与F,G重合),∠EFG=90°,EF=FG=6,,连接CG.
(1)如图1,若点B为EG的中点,且边GF的延长线经过顶点A时,连接BF.求∠BGC的度数.
(2)如图2,若顶点B不是EG中点,且顶点A在边FG上时,作CM⊥EG于点M,BE,.
①求∠BGC的度数;
②连接AC,交BG于点P,求CP的长.
【解答】解:(1)∵∠EFG=90°,FE=FG,B为EG的中点,
∴BF=BG,∠FBG=90°,∠BFG=45°,
∴∠AFB=135°,
∵四边形ABCD为正方形,
∴∠ABC=90°,BA=BC,
∴∠ABC﹣∠FBC=∠FBG﹣∠FBC,
即∠ABF=∠CBG.
在△ABF和△CBG中,
,
∴△ABF≌△CBG(SAS).
∴∠BGC=∠AFB=135°.
(2)①∵∠EFG=90°,FE=FG=6,
∴EG=6.
∵BE=2,,
∴,
∴.
∵CM⊥EG,∠BMC=∠GMC=90°.
∵,BM,
∴CM3,
∴CM=MG,∠MGC=45°,
即∠BGC=45°;
②如图:
∵∠BGC=45°,∠BGA=45°,∠BAC=45°,
∴∠CPG=∠AGP+∠PAG=45°+∠PAG,∠BAG=∠BAC+∠PAG=45°+∠PAG,
∴∠BAG=∠CPG.
又∵∠AGB=∠PGC,
∴△AGB∽△PGC,
∴.
∵,
∴.
∵,CM⊥EG,
∴,
∴,
∴.
19.(2025 泌阳县二模)在学习特殊四边形的过程中,我们对四边形有一些了解,并积累了一定的研究经验.定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.请运用已有经验,对“邻等对补四边形”进行研究.
(1)概念理解
①在以下四种图形中,一定是邻等对补四边形的是 D ;
A.平行四边形
B.菱形
C.矩形
D.正方形
②分别用含有30°和45°角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有 ②④ .(填序号)
(2)概念应用
如图2,∠BAD=60°,且AB=AD.请你用尺规作图在平面内找出动点C的轨迹,使得四边形ABCD总是邻等对补四边形.(保留作图痕迹,不写作法)
(3)综合探究
在(2)的基础上,连接AC,探究线段AC,BC,CD之间满足的数量关系.
【解答】解:(1)根据“邻等对补四边形”的定义,正方形一定是“邻等对补四边形”.
故答案为:D.
②“邻等对补四边形”是②④.
故答案为:②④;
(2)如图,点C在上移动(不与B,D重合)时,四边形ABCD总是邻等对补四边形.
(3)AC=CD+BC.理由如下:如图,延长BC至点E,使得CE=CD,连接ED,DB.
∵AB=AD,∠BAD=60°,
∴△ABD是等边三角形.
∴BD=AD,∠BDA=60°,
∵四边形ABCD是邻等对补四边形,
∴∠BCD=180°﹣∠BAD=120°.
∴∠ECD=60°,
∴△ECD 是等边三角形.
∴ED=CD,∠EDC=60°,
∴∠EDC+∠CDB=∠CDB+∠BDA.
∴∠EDB=∠CDA.
∴△EBD≌△CAD(SAS).
∴AC=EB=EC+CB=CD+BC.
20.(2025 安州区三模)如图,在△ABC中,AC=5,CD为AB边上的高,且CD=BD,tan∠CAB,E,M为AC边上两个不重合的动点(点E在点M的上方,且均不与端点重合),EF∥AB,与边BC交于点F,四边形EMNF为平行四边形,连接BN.
(1)求AD,BD的长.
(2)如图①,若四边形EMNF为菱形,点N在CD上,当tan∠ABN时,求该菱形的边长.
(3)如图②,若BF=BN,则当EF长为多少时,平行四边形EMNF的面积取得最大值?求出最大值.
【解答】解:(1)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∵tan∠CAB,
∴设CD=4x,AD=3x,
∴AC5x=5,
∴x=1,
∴AD=3,CD=4,
∴BD=CD=4;
(2)如图,过点E作EH⊥MN于点H,设EF与CD交于点R,过点M作MG⊥AB于点G,过点N作NK⊥AB于点K.
∵EF∥AB,四边形EMNF为菱形,CD=BD,
∴tan∠CAD=tan∠CER,
∴,即,
设RF=x,则,
∴,
∵四边形EMNF为菱形,
∴,
在Rt△EMH中,,
∴,
∴,
∴,
∴,
∴.
∵,
∴BK=2NK.,
∴.
∵BK=2KN,
∴,
解得,
∴,
∴当时,菱形EMNF 的边长为.
(3)如图,过点B作BP⊥AC于点P,与NF交于点Q,过点E作ET⊥MN于点T.设CD与EF交于点W.
在Rt△ABP中,∠APB=90°AB=3+4=7.
∵,
∴设PB=4a,AP=3a,
∴(4a)2+(3a)2=72,
∴或舍去),
∴,
∴,
当BN=BF时,△BNF是等腰三角形.
∵BP⊥AC,NF∥AC,
∴BQ⊥NF,
∴BQ为△BNF 的中线和高,即NF=2QF.
设WF=m,则,
∴BF=BC﹣CF=42﹣2m,
∵NF∥AC,
∴,即,
解得,
∴ME,
在Rt△EMT中,,
∴,
∴,
同(2)可得EF,S四边形EMNF=EF,
当m=2时,,
∴当EF时,平行四边形EMNF的面积有最大值,最大值为.
21.(2025 姑苏区校级二模)实践探究:两位同学利用菱形纸片进行翻折问题的自主探究,已知纸片为菱形ABCD,其边长为4,一个内角∠A=60°.
(1)如图1,他们将△AMN沿直线MN翻折得到△EMN,使得点E正好落在边CD上,且EM⊥AB,两位同学发现了不同的解法来求出图中线段DN的长度,一位同学找到了图中的一个特殊的等腰三角形,另一位同学则利用轴对称图形对应边相等这一性质;请聪明的你利用提示来求出线段DN的长度;
(2)如图2,两位同学又将△APQ沿直线PQ翻折得到△FPQ,使得点F正好是边CD的中点,那么此时线段DQ的长度是多少呢?
(3)如图3,点G为BC边上一点,将△ABG沿直线AG翻折得到△AKG,BK,AK的延长线分别交CD于S,T两点,若,求线段ST的长度.
【解答】解:(1)法一(利用特殊等腰三角形):
∵菱形ABCD边长为4,∠A=60°,EM⊥AB,
故EM=sin60° AB.
由折叠可知AM=EM,
设AP=x,则PMx,
作NP⊥AB于点P,由EM⊥AB及折叠可知∠EMN=∠PMN=45°,如图1所示,
∴∠PNM=45°,∠ANP=30°,PN=PM,
∴PN,
即x,解得x,
此时AN=2AP,
故DN=AD﹣AN=4﹣().
法二(利用轴对称性质):如图1所示,延长PN交CD延长线于点Q,则PQ⊥CD.
设DN=x,由折叠性质可得AN=4﹣x=NE,
∵∠ANP=∠QND=30°,
∴QN=cos30° DN,
又∵∠QEN=90°﹣∠NEM=90°﹣60°=30°,
∴QN,
故,解得x.
即DN的长度为.
(2)过点Q作MN⊥AB于点N,交CD延长线于点M,如图2所示,
由(1)知MN,
设DQ=x,则AQ=4﹣x=QF,
∵∠MQD=∠MFQ=30°,
∴QM,DM,
在Rt△MQF中,由勾股定理可得 MQ2+MF2=QF2,
即,解得x.
即DQ长为.
(3)由折叠可知AK=AB=4,∠ABK=∠AKB=∠SKT,
∵DC∥AB,
∴∠KST=∠ABK,
故ST=KT.
延长AG交DC的延长线于点R,作AH⊥CD的延长线于点H,如图3所示,
则CG=CB﹣BG=4,
∵CR∥AB,
∴△CRG∽△BAG,
∴,故CR6,
∵CR∥AB,
∴∠R=∠RAB=∠KAR,
∴AT=RT,
设ST=KT=x,则AT=4+x=RT,
∴TC=RT﹣CR=4+x﹣6=x﹣2,
故DS=DC﹣SC=4﹣(2x﹣2)=6﹣2x,
∵∠HAD=30°,
∴DH2,AH=HT=DH+DT=2+6﹣x=8﹣x,
在Rt△AHT中,由勾股定理可得,
解得x,
故ST长为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
