【中考模拟题汇编】查漏补缺:图形的相似-2025年中考数学(含答案)
文档属性
| 名称 | 【中考模拟题汇编】查漏补缺:图形的相似-2025年中考数学(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 05:35:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【中考模拟题汇编】查漏补缺:图形的相似-2025年中考数学
一.选择题(共8小题)
1.(2025 桥东区模拟)如图,带有刻度的直尺结合数轴作图,已知图中的虚线相互平行,若点A与直尺的0刻度重合且在数轴上表示的数是﹣2,则点B在数轴上表示的数是( )
A.2 B.3 C.4 D.5
2.(2025 白云区模拟)如图,在5×4的正方形网格中,点A,C是在网格处,线段AC与网格线交于点B点,则AB:BC等于( )
A.1:2 B. C. D.2:5
3.(2025 北碚区模拟)若两个相似三角形的周长比是2:3,则这两个相似三角形的面积比是( )
A.2:3 B.2:6 C. D.4:9
4.(2025 九龙坡区校级二模)如图,△ABC与△A′B′C′位似,点O为位似中心,若AA′=3OA′,若△A′B′C′的面积为3,则△ABC的面积为( )
A.6 B.9 C.12 D.16
5.(2025 龙泉市二模)如图,在直角坐标系中,△OCD与△OAB是以原点O为位似中心的位似图形,位似比为3.则点A(2,﹣1)的对应点C的坐标为( )
A.(﹣6,3) B.(6,﹣3) C.(﹣3,6) D.(3,﹣6)
6.(2025 河南模拟)手工课上,小明想借助如图所示的四边形纸片剪出一个面积最大的圆形纸片,经测量可得这张四边形纸片中AB=AD=6cm,CB=CD=8cm,∠B为直角,则该圆的半径为( )
A. B. C. D.
7.(2025 南岸区模拟)如图,在正方形ABCD中,对角线AC,BD相交于点O,E是OD的中点,连接CE,过点E作EG⊥EC,EG与AC,AB分别交于点F,G,若EC=EG,则的长为( )
A. B. C.2 D.
8.(2025 西城区校级一模)如图,在等边△ABC中,点D,E分别是边AB、BC上的动点,且BD=2CE.以DE为边作等边△DEF,使点A与点F在直线DE同侧,DF交AC于点G,EF交AC于点H.给出下面四个结论:
①∠BED=∠AHF;
②AD DF=BE DG;
③若ED⊥AB,则DF⊥AC;
④若CE:BE=1:2,则四边形DBEF是菱形.
上述结论中.所有正确结论的序号是( )
A.①② B.③④ C.①②③ D.①②③④
二.填空题(共6小题)
9.(2025 城中区模拟)已知△ABC∽△DEF,且相似比为1:3,则△ABC与△DEF的面积比为 .
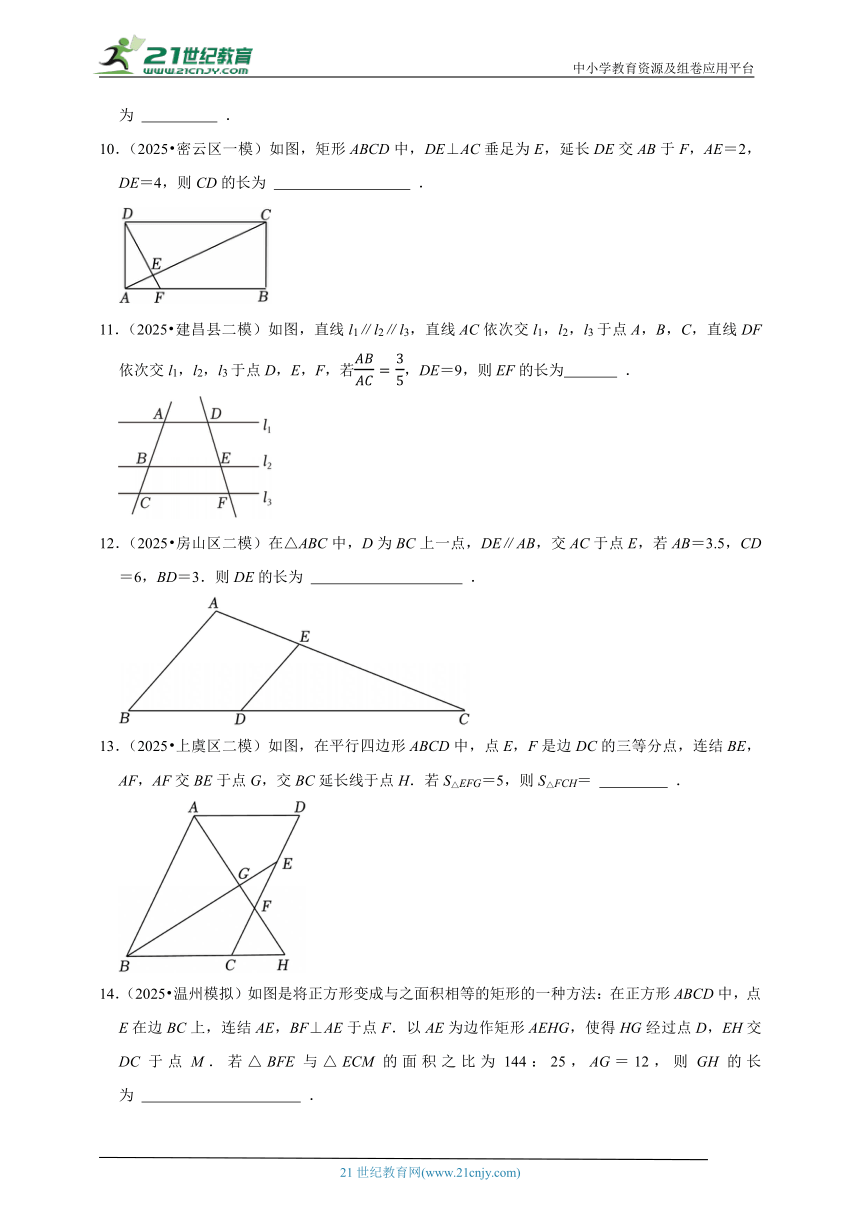
10.(2025 密云区一模)如图,矩形ABCD中,DE⊥AC垂足为E,延长DE交AB于F,AE=2,DE=4,则CD的长为 .
11.(2025 建昌县二模)如图,直线l1∥l2∥l3,直线AC依次交l1,l2,l3于点A,B,C,直线DF依次交l1,l2,l3于点D,E,F,若,DE=9,则EF的长为 .
12.(2025 房山区二模)在△ABC中,D为BC上一点,DE∥AB,交AC于点E,若AB=3.5,CD=6,BD=3.则DE的长为 .
13.(2025 上虞区二模)如图,在平行四边形ABCD中,点E,F是边DC的三等分点,连结BE,AF,AF交BE于点G,交BC延长线于点H.若S△EFG=5,则S△FCH= .
14.(2025 温州模拟)如图是将正方形变成与之面积相等的矩形的一种方法:在正方形ABCD中,点E在边BC上,连结AE,BF⊥AE于点F.以AE为边作矩形AEHG,使得HG经过点D,EH交DC于点M.若△BFE与△ECM的面积之比为144:25,AG=12,则GH的长为 .
三.解答题(共7小题)
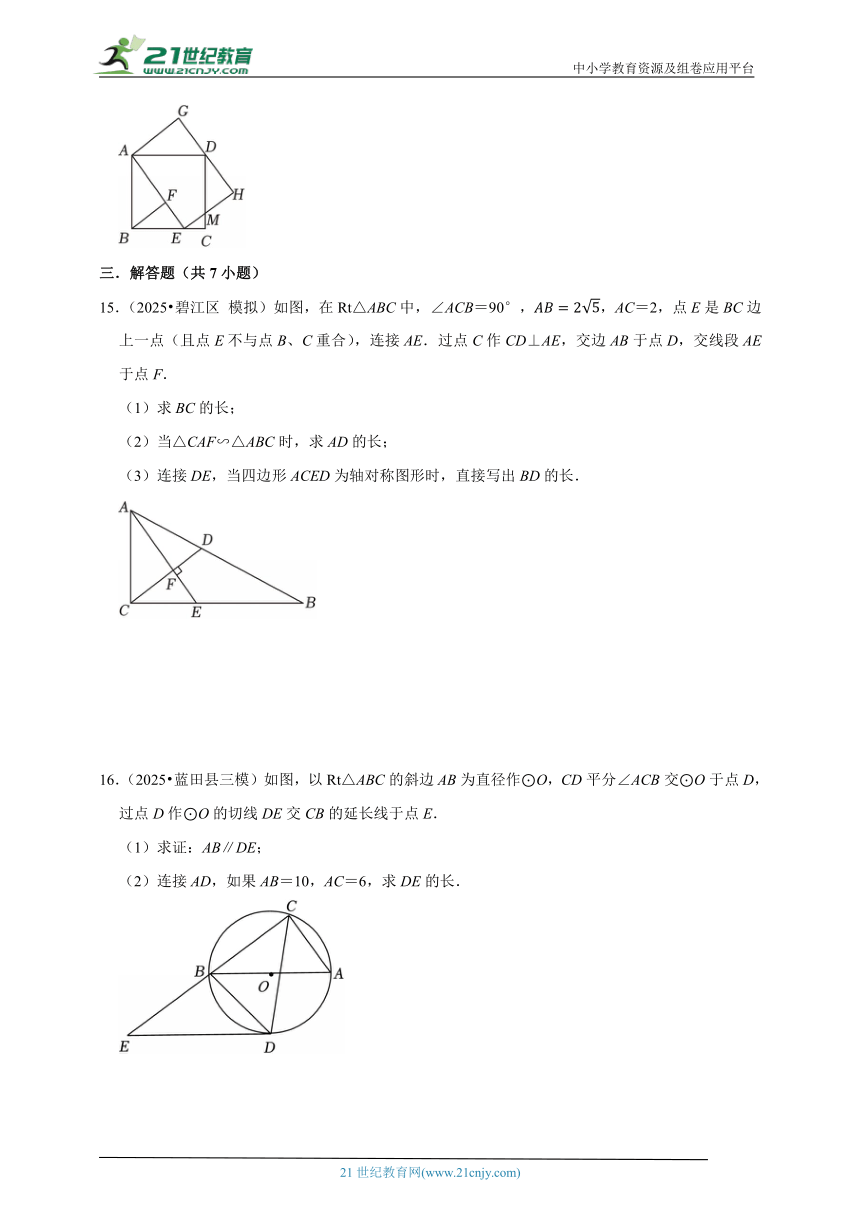
15.(2025 碧江区 模拟)如图,在Rt△ABC中,∠ACB=90°,,AC=2,点E是BC边上一点(且点E不与点B、C重合),连接AE.过点C作CD⊥AE,交边AB于点D,交线段AE于点F.
(1)求BC的长;
(2)当△CAF∽△ABC时,求AD的长;
(3)连接DE,当四边形ACED为轴对称图形时,直接写出BD的长.
16.(2025 蓝田县三模)如图,以Rt△ABC的斜边AB为直径作⊙O,CD平分∠ACB交⊙O于点D,过点D作⊙O的切线DE交CB的延长线于点E.
(1)求证:AB∥DE;
(2)连接AD,如果AB=10,AC=6,求DE的长.
17.(2025 洪山区模拟)如图,在矩形ABCD中,点O是对角线AC和BD的交点,E为线段OB上一点,F为线段OD上一点,连接AE,CE,FC,AF.若 ,则四边形AECF是平行四边形.请从①AE⊥BD,CF⊥BD;②AE=CF;③OE:OB=1:3,FD:OD=2:3这三个选项中选择一个作为条件,使结论成立,并说明理由.
18.(2025 上城区二模)已知:如图,在△ABC中,AB=AC,D,E分别为BC,AB中点,连结DE并延长,使DE=EF.
(1)求证:四边形ADBF为矩形;
(2)记∠ADE=α,∠AEM=β.
①求∠DEM(用含α,β的代数式表示);
②若β=90°﹣2α,求证:2DE2=DM DA.
19.(2025 南岸区模拟)如图,在△ABC中,D是AC边上一点,且AD=AB.AE平分∠BAC,交BC于点F,DE∥AB,DE交BC于点G.DH平分∠CDE,交BC于点H.
(1)求证:DH∥AE;
(2)如图2,当EG=GD,∠DHG=45°时,用等式表示AC与BC之间的数量关系,并证明;
(3)当∠BAD=60°时,连接EH,若△DEH为直角三角形,直接写出的值.
20.(2025 淮安区模拟)【初步感知】如图1,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B时,求证:.
【探索发现】如图2,在△ABC中,∠ABC=50°,AB=4,BC=3,点F是CB延长线上的一点,且BF=BC,在FC下方作∠CFG=∠ABC,将射线CA绕点C逆时针旋转130°,交射线FG于点G,求FG的长.
【尝试应用】如图3,在△ABC中,∠A>∠C,E为AC边上一点,连接BE,∠ABE=∠C,tanC,且,求的值.
【拓展提升】如图4,已知在菱形ABCD中,∠A=60°,点E在边AB上,且AE=mEB,连结CE交对角线BD于F,点G在线段CF上,连结DG,GB,若∠DGB=120°,GB=n,则DG= .(用含有m、n的式子表示)
21.(2025 广信区校级模拟)【综合与实践】
【课本再现】
人教版九年级上册数学教材第60页有一例题:点E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.由作图过程可以得出△ADE≌△ABE′.由此,老师进行了延伸拓展,与同学们一起探究.
【例题延伸】
(1)如图1,在正方形ABCD中,点E,F分别是边BC,CD上的动点,且∠EAF=45°,试判断BE,EF,DF之间的数量关系.小明把△ABE绕点A顺时针旋转90°得到△ADG,使AB与AD重合,试求BE,EF,DF之间有什么数量关系?并说明理由;
【类比探究】
(2)如图2,在矩形ABCD中,已知AB=6,BC=8,点F为边BC延长线上一点,连接DF,过点B作BH⊥DF于点H,交CD于点E.
①求的值;
②求cos∠EFC的值;
【拓展应用】
(3)如图3,在(2)的条件下,平移线段DF,使它经过BE的中点H,交AD于点M,交BC于点N,连接NE,若,请你求出MN的长.
【中考模拟题汇编】查漏补缺:图形的相似-2025年中考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C A D C A A D D
一.选择题(共8小题)
1.(2025 桥东区模拟)如图,带有刻度的直尺结合数轴作图,已知图中的虚线相互平行,若点A与直尺的0刻度重合且在数轴上表示的数是﹣2,则点B在数轴上表示的数是( )
A.2 B.3 C.4 D.5
【解答】解:在数轴上数8对应的点为D,在直尺上刻度3对应的点为C点,刻度5对应的点为D点,如图,
∵BC∥DE,
∴△ABC∽△ADE,
∴,
即,
解得OB=4,
∴点B在数轴上表示的数是4.
故选:C.
2.(2025 白云区模拟)如图,在5×4的正方形网格中,点A,C是在网格处,线段AC与网格线交于点B点,则AB:BC等于( )
A.1:2 B. C. D.2:5
【解答】解:取格点D、E,如图,
∵AD∥CE,
∴△ADE∽△CEB,
∴,
即AB:BC=1:2.
故选:A.
3.(2025 北碚区模拟)若两个相似三角形的周长比是2:3,则这两个相似三角形的面积比是( )
A.2:3 B.2:6 C. D.4:9
【解答】解:根据题意知:两个相似三角形的相似比为2:3,而面积比为相似比的平方,所以面积比是4:9.故选:D.
4.(2025 九龙坡区校级二模)如图,△ABC与△A′B′C′位似,点O为位似中心,若AA′=3OA′,若△A′B′C′的面积为3,则△ABC的面积为( )
A.6 B.9 C.12 D.16
【解答】解:∵AA′=3OA′,
∴2.
∵△ABC与△A′B′C′位似,点O为位似中心,
∴△ABC∽△A′B′C′,且AC∥AA′.
∴22.
∵△A′B′C′的面积为3,
∴△ABC的面积为12,
故选:C.
5.(2025 龙泉市二模)如图,在直角坐标系中,△OCD与△OAB是以原点O为位似中心的位似图形,位似比为3.则点A(2,﹣1)的对应点C的坐标为( )
A.(﹣6,3) B.(6,﹣3) C.(﹣3,6) D.(3,﹣6)
【解答】解:∵△OCD与△OAB是以原点O为位似中心的位似图形,位似比为3,
而A(2,﹣1),
∴点A(2,﹣1)的对应点C的坐标为[﹣3×2,﹣3×(﹣1)],
即C(﹣6,3).
故选:A.
6.(2025 河南模拟)手工课上,小明想借助如图所示的四边形纸片剪出一个面积最大的圆形纸片,经测量可得这张四边形纸片中AB=AD=6cm,CB=CD=8cm,∠B为直角,则该圆的半径为( )
A. B. C. D.
【解答】解:如图,连接AC,作∠ABC的平分线,交AC于点O,作OH⊥BC于H,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,∠ACB=∠ACD,
∴AC平分∠BAD和∠BCD,
∵OB平分∠ABC,
∴点O到四边形ABCD的各边的距离相等,
∴⊙O是四边形ABCD的内切圆,它是所求的面积最大的圆形纸片,其半径为OH,
∵∠ABC=90°,
∴,
∴△BOH为等腰直角三角形,
∴OH=BH,
设OH=r cm,则BH=r cm,CH=BC﹣BH=(8﹣r)cm,
∴∠ABC=90°,OH⊥BC,
∴OH∥AB,
∴△COH∽△CAB,
∴,
即,
∴,
即⊙O的半径为,
∴圆形纸片的半径为,
故选:A.
7.(2025 南岸区模拟)如图,在正方形ABCD中,对角线AC,BD相交于点O,E是OD的中点,连接CE,过点E作EG⊥EC,EG与AC,AB分别交于点F,G,若EC=EG,则的长为( )
A. B. C.2 D.
【解答】解:设OF=m.
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OB=OC=OD,
∵EC⊥EG,
∴∠FEO+∠CEO=90°,∠CEO+∠OCE=90°,
∴∠FEO=∠ECO,
∵E是OD的中点,
∴OE=ED,
∵∠EOF=∠EOC=90°,
∴△EOF∽△COE,
∴,
∴OE=2m,OC=4m,
∴EG=EC2m,EFm,
∴FG=EG﹣EFm,
∴.
故选:D.
8.(2025 西城区校级一模)如图,在等边△ABC中,点D,E分别是边AB、BC上的动点,且BD=2CE.以DE为边作等边△DEF,使点A与点F在直线DE同侧,DF交AC于点G,EF交AC于点H.给出下面四个结论:
①∠BED=∠AHF;
②AD DF=BE DG;
③若ED⊥AB,则DF⊥AC;
④若CE:BE=1:2,则四边形DBEF是菱形.
上述结论中.所有正确结论的序号是( )
A.①② B.③④ C.①②③ D.①②③④
【解答】解:∵△ABC,△DEF都是等边三角形,
∴∠ACB=∠DEF=60°,
∵∠BEF=∠BED+∠DEF=∠ACB+∠CHE,
∴∠BED=∠CHE,
∵∠AHF=∠CHE,
∴∠BED=∠AHF,故①正确;
∵∠B=∠BAC=∠EDF=60°,
∴∠BDE+∠BED=120°,∠BDE+∠ADG=120°,
∴∠BED=∠ADG,
∴△EDB∽△DGA,
∴,即AD DE=BE DG,
∵DE=DF,
∴AD DF=BE DG;故②正确;
∵△ABC是等边三角形,
∴∠B=∠BAC=60°,
∵ED⊥AB,
∴∠ADE=90°,
∵△DEF是等边三角形,
∴∠EDF=60°,
∴∠ADG=30°,
∴∠ADE=90°,
∴∠AGD=90°,即DF⊥AC,故③正确;
∵CE:BE=1:2,
∴BE=2CE,
∵BD=2CE,
∴BE=BE,
∵∠B=60°,
∴△BDE是等边三角形,
∴BE=BD=DE=EF=DF,
∴四边形DBEF是菱形,故④正确.
故选:D.
二.填空题(共6小题)
9.(2025 城中区模拟)已知△ABC∽△DEF,且相似比为1:3,则△ABC与△DEF的面积比为 1:9 .
【解答】解:∵△ABC∽△DEF,且相似比为1:3,
∴△ABC的面积:△DEF的面积=12:32=1:9.
故答案为:1:9.
10.(2025 密云区一模)如图,矩形ABCD中,DE⊥AC垂足为E,延长DE交AB于F,AE=2,DE=4,则CD的长为 4 .
【解答】解:∵DE⊥AC,
∴∠AED=90°,
在Rt△ADE中,∵AE=2,DE=4,
∴AD2,
∵四边形ABCD为矩形,
∴∠ADC=90°,
∵∠ADE+∠CDE=90°,∠ADE+∠DAE=90°,
∴∠CDE=∠DAE,
∴Rt△CDE∽△Rt△DAE,
∴,
即,
解得CD=4.
故答案为:4.
11.(2025 建昌县二模)如图,直线l1∥l2∥l3,直线AC依次交l1,l2,l3于点A,B,C,直线DF依次交l1,l2,l3于点D,E,F,若,DE=9,则EF的长为 6 .
【解答】解:根据平行线分线段成比例可得,
∵,
∴,
解得DF=15,
∴EF=DF﹣DE=6,
故答案为:6.
12.(2025 房山区二模)在△ABC中,D为BC上一点,DE∥AB,交AC于点E,若AB=3.5,CD=6,BD=3.则DE的长为 .
【解答】解:∵DE∥AB,
∴△CED∽△CAB,
∴,
即,
解得DE.
故答案为:.
13.(2025 上虞区二模)如图,在平行四边形ABCD中,点E,F是边DC的三等分点,连结BE,AF,AF交BE于点G,交BC延长线于点H.若S△EFG=5,则S△FCH= 10 .
【解答】解:连接BF,如图,
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∵点E,F是边DC的三等分点,
∴,
∵EF∥AB,
∴△GEF∽△GBA,
∴,()2=()2,
∴S△BGF=3S△GEF=3×5=15,S△GBA=9S△GEF=9×5=45,
∵EF=CF,
∴S△BCF=S△BEF=15+5=20,
∴S四边形ABCF=20+15+45=80,
∵CF∥AB,
∴△HCF∽△HBA,
∴()2=()2,
即,
∴S△HCF=10.
故答案为:10.
14.(2025 温州模拟)如图是将正方形变成与之面积相等的矩形的一种方法:在正方形ABCD中,点E在边BC上,连结AE,BF⊥AE于点F.以AE为边作矩形AEHG,使得HG经过点D,EH交DC于点M.若△BFE与△ECM的面积之比为144:25,AG=12,则GH的长为 .
【解答】解:在正方形ABCD中,AB=AD,∠BAD=90°,
则∠BAE+∠DAE=90°,
在矩形AEHG中,∠EAG=∠G=90°,
则∠DAG+∠DAE=90°,
∴∠BAE=∠DAG,
∵BF⊥AE,
∴∠BFA=90°,
∴△ABF≌△ADG(AAS),
∴AF=AG=12,BF=DG,
∵正方形ABCD与矩形AEHG面积相等,
∴S△BEF+S△ECM=S△DMH,
∵△BFE与△ECM的面积之比为144:25,
设S△ECM=25a,S△BEF=144a,
则S△DMH=S△BEF+S△ECM=169a,
∵BF∥EH,
∴∠FBE=∠MEC,
∵∠BFE=90°=∠C,
∴△BFE∽﹣△ECM,
则;
∴∠EMC=∠DMH,
∵∠H=90°=∠C,
∴△MHD∽△MCE,
则,
设EC=5b,则HD=13b,BF=12b,
∴DG=BF=12b,
在Rt△ABF中,∠AFB=90°,AF=12,BF=12b,
则由勾股定理可得,
∴,
∵GH=GD+DH=12b+13b=25b,
∴S矩形AEHG=AG GH=25b×12=300b,
∵正方形ABCD与矩形AEHG面积相等,
∴300b=144(b2+1),
即12b2﹣25b+12=0,
∴,
解得或,
∵在正方形ABCD中,当点E与点C重合时,△ABC是等腰直角三角形,
则由BF⊥AE可知,此时AF=BF,
∴当点E在边BC上时,AF>BF,即12>12b,
解得b<1,
∴取,
则,
故答案为:.
三.解答题(共7小题)
15.(2025 碧江区 模拟)如图,在Rt△ABC中,∠ACB=90°,,AC=2,点E是BC边上一点(且点E不与点B、C重合),连接AE.过点C作CD⊥AE,交边AB于点D,交线段AE于点F.
(1)求BC的长;
(2)当△CAF∽△ABC时,求AD的长;
(3)连接DE,当四边形ACED为轴对称图形时,直接写出BD的长.
【解答】解:(1)在Rt△ABC中,∠ACB=90°,AB=2,AC=2,
∴BC4;
(2)当△CAF∽△ABC时,
∴∠CAF=∠B,
∵AE⊥CD,∠ACB=90°,
∴∠CAF+∠ACF=90°,∠ACF+∠FCB=90°,
∴∠CAF=∠FCB=∠B,
∴AD=BDAB;
(3)当四边形ACED为轴对称图形时,
①如图,以AE为对称轴时,
则AD=AC=2,
∴BD=AB﹣AD=22;
②如图,以CD为对称轴时,
则∠ACD=∠BCD,
∴点D到AC、BC的距离相等,
设点D到AC、BC的距离为h,点C到AB的距离为m,
∴,
∴,
∴BD,
综上,BD的长为22或
16.(2025 蓝田县三模)如图,以Rt△ABC的斜边AB为直径作⊙O,CD平分∠ACB交⊙O于点D,过点D作⊙O的切线DE交CB的延长线于点E.
(1)求证:AB∥DE;
(2)连接AD,如果AB=10,AC=6,求DE的长.
【解答】(1)证明:连接OD,如图,
∵AB为直径,
∴∠BCA=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴∠BOD=2∠BCD=90°,
∴OD⊥AB,
∵DE为⊙O的切线,
∴OD⊥DE,
∴AB∥DE;
(2)解:在Rt△ABC中,∵AB=10,AC=6,
∴BC8,
∵AB为直径,
∴∠BDA=90°,
∵∠DBA=∠ACD=45°,
∴△ABD为等腰直角三角形,
∴BD=ADAB=5,
∵AB∥DE,
∴∠E=∠ABC,∠EDB=∠DBA=45°,
而∠ABC=∠ADC,
∴∠E=∠ADC,
∵∠ACD=∠EDB=45°,
∴△EDB∽△DCA,
∴BE:AD=BD:AC,
即BE:55:6,
解得BE,
∴CE=BE+BC8,
∵∠EDB=∠ECD,∠DEB=∠CED,
∴△EDB∽△ECD,
∴DE:EC=BE:DE,
即DE::DE,
解得DE.
17.(2025 洪山区模拟)如图,在矩形ABCD中,点O是对角线AC和BD的交点,E为线段OB上一点,F为线段OD上一点,连接AE,CE,FC,AF.若 OE:OB=1:3,FD:OD=2:3 ,则四边形AECF是平行四边形.请从①AE⊥BD,CF⊥BD;②AE=CF;③OE:OB=1:3,FD:OD=2:3这三个选项中选择一个作为条件,使结论成立,并说明理由.
【解答】解:选择③OE:OB=1:3,FD:OD=2:3,
理由:∵四边形ABCD是矩形,对角线AC、BD交于点O,
∴OA=OC,OB=OD,
∴OBOD,
∵OE:OB=1:3,FD:OD=2:3,
∴OEOB,FDOD,
∴OF=ODODOD,
∴OE=OF,
∵OA=OC,OE=OF,
∴四边形AECF是平行四边形,
故答案为:OE:OB=1:3,FD:OD=2:3.
注:答案不唯一.
18.(2025 上城区二模)已知:如图,在△ABC中,AB=AC,D,E分别为BC,AB中点,连结DE并延长,使DE=EF.
(1)求证:四边形ADBF为矩形;
(2)记∠ADE=α,∠AEM=β.
①求∠DEM(用含α,β的代数式表示);
②若β=90°﹣2α,求证:2DE2=DM DA.
【解答】(1)证明:∵AB=AC,点D为BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∵点E为AB的中点,
∴DE=BE=AE,
∵DE=EF,
∴DE=EF=BE=AE,
∴四边形ADBF为矩形;
(2)①解:∵EA=ED,
∴∠EAD=∠ADE=α,
∴∠AED=180°﹣2α,
∴∠DEM=∠AED﹣∠AEM=180°﹣2α﹣β;
②证明:∵β=90°﹣2α,
∴∠DEM=180°﹣2α﹣β=180°﹣2α﹣(90°﹣2α)=90°,
∵四边形ADBF为矩形,
∴∠DAF=90°,
∵∠MDE=∠FDA,∠DEM=∠DAF,
∴△DEM∽△DAF,
∴DE:DA=DM:DF,
∴DE DF=DM DA,
而DF=2DE,
∴2DE2=DM DA.
19.(2025 南岸区模拟)如图,在△ABC中,D是AC边上一点,且AD=AB.AE平分∠BAC,交BC于点F,DE∥AB,DE交BC于点G.DH平分∠CDE,交BC于点H.
(1)求证:DH∥AE;
(2)如图2,当EG=GD,∠DHG=45°时,用等式表示AC与BC之间的数量关系,并证明;
(3)当∠BAD=60°时,连接EH,若△DEH为直角三角形,直接写出的值.
【解答】(1)证明:∵DE∥AB,
∴∠CAB=∠CDE,
又∵AE平分∠BAC,DH平分∠CDE,
∴,∠EDH=∠CDH,
∴∠CAE=∠CDH,
∴DH∥AE;
(2)解:,证明如下:
连接BD交AE于点O,连接BE,如图,
∵DE∥AB,
∴∠DEA=∠EAB,
又∵∠BAE=∠CAE,
∴∠DEA=∠CAE,
∴DE=DA=AB,
∴四边形ABED是菱形,
∴∠BOF=90°,BO=OD,BE∥AC,BE=AD,
∴∠BED=∠EDC,∠EBC=∠C,
又∵EG=GD,
∴△GEB≌△GDC(ASA),
∴BE=CD,BG=GC,
同理可得△GEF≌△GDH(ASA),
∴FG=GH,
设EO=OD=a,
∵DH∥AE,
∴∠BFO=∠GHD=45°,∠BOF=∠BDH=90°,
∴BO=OF=a,BD=DH=2OB=2a,
∴BFa,,
∴,
∴,
∴,
即,
又∵DH∥AE,
∴△CDH∽△CAF,
∴,
即AF=2DH=4a,
∴AO=AF﹣OF=4a﹣a=3a,
∴,
∴,
∴;
(3)解:∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
连BD交AE于M,如图,
由(2)可得:∠BAF=∠FAD=∠AED=30°,∠BMF=∠BDH=90°,BO=OD,
①当∠DHE=90°时,四边形DMEH是矩形,
∴DM=EH,DE=2DM=2EH,HE∥DM,
∴∠EHG=∠GBD,∠HEG=∠GDB,
∴△EHG∽△DBG,
∴,
∴DGDEEH,
∴;
②当∠HED=90°时,ED=2DM,
∴,
又∵DH∥AE,
∴∠HDE=∠MCD=30°,
∴,
∴,
又∵AE∥DH,
∴△BMF∽△BDH,
∴,
即,
∴,
又∵AE∥DH,
∴∠FEG=∠GDH,∠EFG=∠GHD,
∴△GEF∽△GDH,
∴,
∴,
∴;
综上,△DEH为直角三角形时,的值为或.
20.(2025 淮安区模拟)【初步感知】如图1,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B时,求证:.
【探索发现】如图2,在△ABC中,∠ABC=50°,AB=4,BC=3,点F是CB延长线上的一点,且BF=BC,在FC下方作∠CFG=∠ABC,将射线CA绕点C逆时针旋转130°,交射线FG于点G,求FG的长.
【尝试应用】如图3,在△ABC中,∠A>∠C,E为AC边上一点,连接BE,∠ABE=∠C,tanC,且,求的值.
【拓展提升】如图4,已知在菱形ABCD中,∠A=60°,点E在边AB上,且AE=mEB,连结CE交对角线BD于F,点G在线段CF上,连结DG,GB,若∠DGB=120°,GB=n,则DG= n .(用含有m、n的式子表示)
【解答】【初步感知】证明:∵∠DPC=∠A=∠B,∠APD+∠ADP=180°﹣∠A,∠APD+∠BPC=180°﹣∠DPC,
∴∠ADP=∠PBC,
∴△APD∽△BCP,
∴;
【探索发现】解:∵∠ABC=50°,
∴∠A+∠ACB=130°,
∵射线CA绕点C逆时针旋转130°,交射线FG于点G,
∴∠ACG=130°,
∴∠ACB+∠FCG=130°,
∴∠A=∠FCG,
∵∠CFG=∠ABC,
∴△ABC∽△CFG,
∴,
∵BF=BC=3,
∴CF=6,
∴,
∴FG;
【尝试应用】解:如图1,
作AD⊥BC于D,
设CE=3a,AE=7a,则AC=10a,
∵tanC,
∴sinC,cosC,
∴ADAC=8a,CDAC=6a,
∵∠ABE=∠C,∠BAC=∠BAE,
∴△ABE∽△ACB,
∴,
∴AB2=AE AC=70a2,
∴BD,
∴BC=CD+BD=(6)a,
∴;
【拓展提升】解:如图2,
作GV∥BD,交CD于V,交BC于W,
∴△CGV∽△CFD,△CGW∽△CFB,
∴,
∵四边形ABCD是菱形,
∴CD∥AB,CD=AB=BC,∠BCD=∠A=60°,
∴△BEF∽△DCG,△BCD是等边三角形,
∴,∠CDB=∠CBD=60°,
∴,∠DVG=∠BWG=120°,CV=CW,
∴∠WBG+∠BGW=60°,DV=BW,
∵∠DGB=120°,
∴∠BGW+∠DGV=60°,
∴∠DGV=∠WBG,
∴△DGV∽△GBW,
∴,
设GW=x,GW=(m+1)x,
∴,
∴DV x,
∴,
∴DG,
故答案为:n.
21.(2025 广信区校级模拟)【综合与实践】
【课本再现】
人教版九年级上册数学教材第60页有一例题:点E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.由作图过程可以得出△ADE≌△ABE′.由此,老师进行了延伸拓展,与同学们一起探究.
【例题延伸】
(1)如图1,在正方形ABCD中,点E,F分别是边BC,CD上的动点,且∠EAF=45°,试判断BE,EF,DF之间的数量关系.小明把△ABE绕点A顺时针旋转90°得到△ADG,使AB与AD重合,试求BE,EF,DF之间有什么数量关系?并说明理由;
【类比探究】
(2)如图2,在矩形ABCD中,已知AB=6,BC=8,点F为边BC延长线上一点,连接DF,过点B作BH⊥DF于点H,交CD于点E.
①求的值;
②求cos∠EFC的值;
【拓展应用】
(3)如图3,在(2)的条件下,平移线段DF,使它经过BE的中点H,交AD于点M,交BC于点N,连接NE,若,请你求出MN的长.
【解答】解:(1)EF=BE+DF;理由如下:
∵△ADG是△ABE绕点A顺时针旋转90°得到的,
∴∠ADG=∠B,AG=AE,∠DAG=∠BAE.
∵四边形ABCD是正方形,
∴∠B=∠BAD=∠ADC=90°,AB=AD,
∴∠ADG=90°,
∴∠ADG+∠ADC=180°,
∴C,D,G三点共线.
∵∠EAF=45°,∠BAD=90°,
∴∠BAE+∠DAF=45°,
∴∠DAG+∠DAF=45°,
∴∠GAF=45°,
∴∠GAF=∠EAF.
在△EAF和△GAF中,
,
∴△EAF≌△GAF(SAS),
∴EF=FG=DG+DF=BE+DF;
(2)①∵BE⊥DF,
∴∠CBE+∠DFC=90°.
在矩形ABCD中,∠DCF=∠DCB=90°,AB=CD,
∴∠CBE+∠BEC=90°,
∴∠BEC=∠DFC,
∴△BCE∽△DCF,
∴.
∵,
∴;
②∵△BCE∽△DCF,,
∴.
设CE=4a,则CF=3a,
在直角三角形CEF中,由勾股定理得:,
∴;
(3)由平移的性质可得MN∥DF,MN=DF.
∵点H为BE的中点,
∴MN垂直平分BE,
∴BN=NE.
∵,
∴设BN=EN=5x,CE=4x,
在直角三角形CEN中,由勾股定理得:,
∴BC=BN+CN=8x.
∵BC=8,
∴8x=8,
解得x=1,
∴CE=4.
∵,设MN=3y,
∴BE=4y.
在Rt△EBC中,由勾股定理得:BE2=BC2+CE2,
∴(4y)2=42+82,
解得或(不合题意,舍去),
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【中考模拟题汇编】查漏补缺:图形的相似-2025年中考数学
一.选择题(共8小题)
1.(2025 桥东区模拟)如图,带有刻度的直尺结合数轴作图,已知图中的虚线相互平行,若点A与直尺的0刻度重合且在数轴上表示的数是﹣2,则点B在数轴上表示的数是( )
A.2 B.3 C.4 D.5
2.(2025 白云区模拟)如图,在5×4的正方形网格中,点A,C是在网格处,线段AC与网格线交于点B点,则AB:BC等于( )
A.1:2 B. C. D.2:5
3.(2025 北碚区模拟)若两个相似三角形的周长比是2:3,则这两个相似三角形的面积比是( )
A.2:3 B.2:6 C. D.4:9
4.(2025 九龙坡区校级二模)如图,△ABC与△A′B′C′位似,点O为位似中心,若AA′=3OA′,若△A′B′C′的面积为3,则△ABC的面积为( )
A.6 B.9 C.12 D.16
5.(2025 龙泉市二模)如图,在直角坐标系中,△OCD与△OAB是以原点O为位似中心的位似图形,位似比为3.则点A(2,﹣1)的对应点C的坐标为( )
A.(﹣6,3) B.(6,﹣3) C.(﹣3,6) D.(3,﹣6)
6.(2025 河南模拟)手工课上,小明想借助如图所示的四边形纸片剪出一个面积最大的圆形纸片,经测量可得这张四边形纸片中AB=AD=6cm,CB=CD=8cm,∠B为直角,则该圆的半径为( )
A. B. C. D.
7.(2025 南岸区模拟)如图,在正方形ABCD中,对角线AC,BD相交于点O,E是OD的中点,连接CE,过点E作EG⊥EC,EG与AC,AB分别交于点F,G,若EC=EG,则的长为( )
A. B. C.2 D.
8.(2025 西城区校级一模)如图,在等边△ABC中,点D,E分别是边AB、BC上的动点,且BD=2CE.以DE为边作等边△DEF,使点A与点F在直线DE同侧,DF交AC于点G,EF交AC于点H.给出下面四个结论:
①∠BED=∠AHF;
②AD DF=BE DG;
③若ED⊥AB,则DF⊥AC;
④若CE:BE=1:2,则四边形DBEF是菱形.
上述结论中.所有正确结论的序号是( )
A.①② B.③④ C.①②③ D.①②③④
二.填空题(共6小题)
9.(2025 城中区模拟)已知△ABC∽△DEF,且相似比为1:3,则△ABC与△DEF的面积比为 .
10.(2025 密云区一模)如图,矩形ABCD中,DE⊥AC垂足为E,延长DE交AB于F,AE=2,DE=4,则CD的长为 .
11.(2025 建昌县二模)如图,直线l1∥l2∥l3,直线AC依次交l1,l2,l3于点A,B,C,直线DF依次交l1,l2,l3于点D,E,F,若,DE=9,则EF的长为 .
12.(2025 房山区二模)在△ABC中,D为BC上一点,DE∥AB,交AC于点E,若AB=3.5,CD=6,BD=3.则DE的长为 .
13.(2025 上虞区二模)如图,在平行四边形ABCD中,点E,F是边DC的三等分点,连结BE,AF,AF交BE于点G,交BC延长线于点H.若S△EFG=5,则S△FCH= .
14.(2025 温州模拟)如图是将正方形变成与之面积相等的矩形的一种方法:在正方形ABCD中,点E在边BC上,连结AE,BF⊥AE于点F.以AE为边作矩形AEHG,使得HG经过点D,EH交DC于点M.若△BFE与△ECM的面积之比为144:25,AG=12,则GH的长为 .
三.解答题(共7小题)
15.(2025 碧江区 模拟)如图,在Rt△ABC中,∠ACB=90°,,AC=2,点E是BC边上一点(且点E不与点B、C重合),连接AE.过点C作CD⊥AE,交边AB于点D,交线段AE于点F.
(1)求BC的长;
(2)当△CAF∽△ABC时,求AD的长;
(3)连接DE,当四边形ACED为轴对称图形时,直接写出BD的长.
16.(2025 蓝田县三模)如图,以Rt△ABC的斜边AB为直径作⊙O,CD平分∠ACB交⊙O于点D,过点D作⊙O的切线DE交CB的延长线于点E.
(1)求证:AB∥DE;
(2)连接AD,如果AB=10,AC=6,求DE的长.
17.(2025 洪山区模拟)如图,在矩形ABCD中,点O是对角线AC和BD的交点,E为线段OB上一点,F为线段OD上一点,连接AE,CE,FC,AF.若 ,则四边形AECF是平行四边形.请从①AE⊥BD,CF⊥BD;②AE=CF;③OE:OB=1:3,FD:OD=2:3这三个选项中选择一个作为条件,使结论成立,并说明理由.
18.(2025 上城区二模)已知:如图,在△ABC中,AB=AC,D,E分别为BC,AB中点,连结DE并延长,使DE=EF.
(1)求证:四边形ADBF为矩形;
(2)记∠ADE=α,∠AEM=β.
①求∠DEM(用含α,β的代数式表示);
②若β=90°﹣2α,求证:2DE2=DM DA.
19.(2025 南岸区模拟)如图,在△ABC中,D是AC边上一点,且AD=AB.AE平分∠BAC,交BC于点F,DE∥AB,DE交BC于点G.DH平分∠CDE,交BC于点H.
(1)求证:DH∥AE;
(2)如图2,当EG=GD,∠DHG=45°时,用等式表示AC与BC之间的数量关系,并证明;
(3)当∠BAD=60°时,连接EH,若△DEH为直角三角形,直接写出的值.
20.(2025 淮安区模拟)【初步感知】如图1,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B时,求证:.
【探索发现】如图2,在△ABC中,∠ABC=50°,AB=4,BC=3,点F是CB延长线上的一点,且BF=BC,在FC下方作∠CFG=∠ABC,将射线CA绕点C逆时针旋转130°,交射线FG于点G,求FG的长.
【尝试应用】如图3,在△ABC中,∠A>∠C,E为AC边上一点,连接BE,∠ABE=∠C,tanC,且,求的值.
【拓展提升】如图4,已知在菱形ABCD中,∠A=60°,点E在边AB上,且AE=mEB,连结CE交对角线BD于F,点G在线段CF上,连结DG,GB,若∠DGB=120°,GB=n,则DG= .(用含有m、n的式子表示)
21.(2025 广信区校级模拟)【综合与实践】
【课本再现】
人教版九年级上册数学教材第60页有一例题:点E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.由作图过程可以得出△ADE≌△ABE′.由此,老师进行了延伸拓展,与同学们一起探究.
【例题延伸】
(1)如图1,在正方形ABCD中,点E,F分别是边BC,CD上的动点,且∠EAF=45°,试判断BE,EF,DF之间的数量关系.小明把△ABE绕点A顺时针旋转90°得到△ADG,使AB与AD重合,试求BE,EF,DF之间有什么数量关系?并说明理由;
【类比探究】
(2)如图2,在矩形ABCD中,已知AB=6,BC=8,点F为边BC延长线上一点,连接DF,过点B作BH⊥DF于点H,交CD于点E.
①求的值;
②求cos∠EFC的值;
【拓展应用】
(3)如图3,在(2)的条件下,平移线段DF,使它经过BE的中点H,交AD于点M,交BC于点N,连接NE,若,请你求出MN的长.
【中考模拟题汇编】查漏补缺:图形的相似-2025年中考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C A D C A A D D
一.选择题(共8小题)
1.(2025 桥东区模拟)如图,带有刻度的直尺结合数轴作图,已知图中的虚线相互平行,若点A与直尺的0刻度重合且在数轴上表示的数是﹣2,则点B在数轴上表示的数是( )
A.2 B.3 C.4 D.5
【解答】解:在数轴上数8对应的点为D,在直尺上刻度3对应的点为C点,刻度5对应的点为D点,如图,
∵BC∥DE,
∴△ABC∽△ADE,
∴,
即,
解得OB=4,
∴点B在数轴上表示的数是4.
故选:C.
2.(2025 白云区模拟)如图,在5×4的正方形网格中,点A,C是在网格处,线段AC与网格线交于点B点,则AB:BC等于( )
A.1:2 B. C. D.2:5
【解答】解:取格点D、E,如图,
∵AD∥CE,
∴△ADE∽△CEB,
∴,
即AB:BC=1:2.
故选:A.
3.(2025 北碚区模拟)若两个相似三角形的周长比是2:3,则这两个相似三角形的面积比是( )
A.2:3 B.2:6 C. D.4:9
【解答】解:根据题意知:两个相似三角形的相似比为2:3,而面积比为相似比的平方,所以面积比是4:9.故选:D.
4.(2025 九龙坡区校级二模)如图,△ABC与△A′B′C′位似,点O为位似中心,若AA′=3OA′,若△A′B′C′的面积为3,则△ABC的面积为( )
A.6 B.9 C.12 D.16
【解答】解:∵AA′=3OA′,
∴2.
∵△ABC与△A′B′C′位似,点O为位似中心,
∴△ABC∽△A′B′C′,且AC∥AA′.
∴22.
∵△A′B′C′的面积为3,
∴△ABC的面积为12,
故选:C.
5.(2025 龙泉市二模)如图,在直角坐标系中,△OCD与△OAB是以原点O为位似中心的位似图形,位似比为3.则点A(2,﹣1)的对应点C的坐标为( )
A.(﹣6,3) B.(6,﹣3) C.(﹣3,6) D.(3,﹣6)
【解答】解:∵△OCD与△OAB是以原点O为位似中心的位似图形,位似比为3,
而A(2,﹣1),
∴点A(2,﹣1)的对应点C的坐标为[﹣3×2,﹣3×(﹣1)],
即C(﹣6,3).
故选:A.
6.(2025 河南模拟)手工课上,小明想借助如图所示的四边形纸片剪出一个面积最大的圆形纸片,经测量可得这张四边形纸片中AB=AD=6cm,CB=CD=8cm,∠B为直角,则该圆的半径为( )
A. B. C. D.
【解答】解:如图,连接AC,作∠ABC的平分线,交AC于点O,作OH⊥BC于H,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,∠ACB=∠ACD,
∴AC平分∠BAD和∠BCD,
∵OB平分∠ABC,
∴点O到四边形ABCD的各边的距离相等,
∴⊙O是四边形ABCD的内切圆,它是所求的面积最大的圆形纸片,其半径为OH,
∵∠ABC=90°,
∴,
∴△BOH为等腰直角三角形,
∴OH=BH,
设OH=r cm,则BH=r cm,CH=BC﹣BH=(8﹣r)cm,
∴∠ABC=90°,OH⊥BC,
∴OH∥AB,
∴△COH∽△CAB,
∴,
即,
∴,
即⊙O的半径为,
∴圆形纸片的半径为,
故选:A.
7.(2025 南岸区模拟)如图,在正方形ABCD中,对角线AC,BD相交于点O,E是OD的中点,连接CE,过点E作EG⊥EC,EG与AC,AB分别交于点F,G,若EC=EG,则的长为( )
A. B. C.2 D.
【解答】解:设OF=m.
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OB=OC=OD,
∵EC⊥EG,
∴∠FEO+∠CEO=90°,∠CEO+∠OCE=90°,
∴∠FEO=∠ECO,
∵E是OD的中点,
∴OE=ED,
∵∠EOF=∠EOC=90°,
∴△EOF∽△COE,
∴,
∴OE=2m,OC=4m,
∴EG=EC2m,EFm,
∴FG=EG﹣EFm,
∴.
故选:D.
8.(2025 西城区校级一模)如图,在等边△ABC中,点D,E分别是边AB、BC上的动点,且BD=2CE.以DE为边作等边△DEF,使点A与点F在直线DE同侧,DF交AC于点G,EF交AC于点H.给出下面四个结论:
①∠BED=∠AHF;
②AD DF=BE DG;
③若ED⊥AB,则DF⊥AC;
④若CE:BE=1:2,则四边形DBEF是菱形.
上述结论中.所有正确结论的序号是( )
A.①② B.③④ C.①②③ D.①②③④
【解答】解:∵△ABC,△DEF都是等边三角形,
∴∠ACB=∠DEF=60°,
∵∠BEF=∠BED+∠DEF=∠ACB+∠CHE,
∴∠BED=∠CHE,
∵∠AHF=∠CHE,
∴∠BED=∠AHF,故①正确;
∵∠B=∠BAC=∠EDF=60°,
∴∠BDE+∠BED=120°,∠BDE+∠ADG=120°,
∴∠BED=∠ADG,
∴△EDB∽△DGA,
∴,即AD DE=BE DG,
∵DE=DF,
∴AD DF=BE DG;故②正确;
∵△ABC是等边三角形,
∴∠B=∠BAC=60°,
∵ED⊥AB,
∴∠ADE=90°,
∵△DEF是等边三角形,
∴∠EDF=60°,
∴∠ADG=30°,
∴∠ADE=90°,
∴∠AGD=90°,即DF⊥AC,故③正确;
∵CE:BE=1:2,
∴BE=2CE,
∵BD=2CE,
∴BE=BE,
∵∠B=60°,
∴△BDE是等边三角形,
∴BE=BD=DE=EF=DF,
∴四边形DBEF是菱形,故④正确.
故选:D.
二.填空题(共6小题)
9.(2025 城中区模拟)已知△ABC∽△DEF,且相似比为1:3,则△ABC与△DEF的面积比为 1:9 .
【解答】解:∵△ABC∽△DEF,且相似比为1:3,
∴△ABC的面积:△DEF的面积=12:32=1:9.
故答案为:1:9.
10.(2025 密云区一模)如图,矩形ABCD中,DE⊥AC垂足为E,延长DE交AB于F,AE=2,DE=4,则CD的长为 4 .
【解答】解:∵DE⊥AC,
∴∠AED=90°,
在Rt△ADE中,∵AE=2,DE=4,
∴AD2,
∵四边形ABCD为矩形,
∴∠ADC=90°,
∵∠ADE+∠CDE=90°,∠ADE+∠DAE=90°,
∴∠CDE=∠DAE,
∴Rt△CDE∽△Rt△DAE,
∴,
即,
解得CD=4.
故答案为:4.
11.(2025 建昌县二模)如图,直线l1∥l2∥l3,直线AC依次交l1,l2,l3于点A,B,C,直线DF依次交l1,l2,l3于点D,E,F,若,DE=9,则EF的长为 6 .
【解答】解:根据平行线分线段成比例可得,
∵,
∴,
解得DF=15,
∴EF=DF﹣DE=6,
故答案为:6.
12.(2025 房山区二模)在△ABC中,D为BC上一点,DE∥AB,交AC于点E,若AB=3.5,CD=6,BD=3.则DE的长为 .
【解答】解:∵DE∥AB,
∴△CED∽△CAB,
∴,
即,
解得DE.
故答案为:.
13.(2025 上虞区二模)如图,在平行四边形ABCD中,点E,F是边DC的三等分点,连结BE,AF,AF交BE于点G,交BC延长线于点H.若S△EFG=5,则S△FCH= 10 .
【解答】解:连接BF,如图,
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∵点E,F是边DC的三等分点,
∴,
∵EF∥AB,
∴△GEF∽△GBA,
∴,()2=()2,
∴S△BGF=3S△GEF=3×5=15,S△GBA=9S△GEF=9×5=45,
∵EF=CF,
∴S△BCF=S△BEF=15+5=20,
∴S四边形ABCF=20+15+45=80,
∵CF∥AB,
∴△HCF∽△HBA,
∴()2=()2,
即,
∴S△HCF=10.
故答案为:10.
14.(2025 温州模拟)如图是将正方形变成与之面积相等的矩形的一种方法:在正方形ABCD中,点E在边BC上,连结AE,BF⊥AE于点F.以AE为边作矩形AEHG,使得HG经过点D,EH交DC于点M.若△BFE与△ECM的面积之比为144:25,AG=12,则GH的长为 .
【解答】解:在正方形ABCD中,AB=AD,∠BAD=90°,
则∠BAE+∠DAE=90°,
在矩形AEHG中,∠EAG=∠G=90°,
则∠DAG+∠DAE=90°,
∴∠BAE=∠DAG,
∵BF⊥AE,
∴∠BFA=90°,
∴△ABF≌△ADG(AAS),
∴AF=AG=12,BF=DG,
∵正方形ABCD与矩形AEHG面积相等,
∴S△BEF+S△ECM=S△DMH,
∵△BFE与△ECM的面积之比为144:25,
设S△ECM=25a,S△BEF=144a,
则S△DMH=S△BEF+S△ECM=169a,
∵BF∥EH,
∴∠FBE=∠MEC,
∵∠BFE=90°=∠C,
∴△BFE∽﹣△ECM,
则;
∴∠EMC=∠DMH,
∵∠H=90°=∠C,
∴△MHD∽△MCE,
则,
设EC=5b,则HD=13b,BF=12b,
∴DG=BF=12b,
在Rt△ABF中,∠AFB=90°,AF=12,BF=12b,
则由勾股定理可得,
∴,
∵GH=GD+DH=12b+13b=25b,
∴S矩形AEHG=AG GH=25b×12=300b,
∵正方形ABCD与矩形AEHG面积相等,
∴300b=144(b2+1),
即12b2﹣25b+12=0,
∴,
解得或,
∵在正方形ABCD中,当点E与点C重合时,△ABC是等腰直角三角形,
则由BF⊥AE可知,此时AF=BF,
∴当点E在边BC上时,AF>BF,即12>12b,
解得b<1,
∴取,
则,
故答案为:.
三.解答题(共7小题)
15.(2025 碧江区 模拟)如图,在Rt△ABC中,∠ACB=90°,,AC=2,点E是BC边上一点(且点E不与点B、C重合),连接AE.过点C作CD⊥AE,交边AB于点D,交线段AE于点F.
(1)求BC的长;
(2)当△CAF∽△ABC时,求AD的长;
(3)连接DE,当四边形ACED为轴对称图形时,直接写出BD的长.
【解答】解:(1)在Rt△ABC中,∠ACB=90°,AB=2,AC=2,
∴BC4;
(2)当△CAF∽△ABC时,
∴∠CAF=∠B,
∵AE⊥CD,∠ACB=90°,
∴∠CAF+∠ACF=90°,∠ACF+∠FCB=90°,
∴∠CAF=∠FCB=∠B,
∴AD=BDAB;
(3)当四边形ACED为轴对称图形时,
①如图,以AE为对称轴时,
则AD=AC=2,
∴BD=AB﹣AD=22;
②如图,以CD为对称轴时,
则∠ACD=∠BCD,
∴点D到AC、BC的距离相等,
设点D到AC、BC的距离为h,点C到AB的距离为m,
∴,
∴,
∴BD,
综上,BD的长为22或
16.(2025 蓝田县三模)如图,以Rt△ABC的斜边AB为直径作⊙O,CD平分∠ACB交⊙O于点D,过点D作⊙O的切线DE交CB的延长线于点E.
(1)求证:AB∥DE;
(2)连接AD,如果AB=10,AC=6,求DE的长.
【解答】(1)证明:连接OD,如图,
∵AB为直径,
∴∠BCA=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴∠BOD=2∠BCD=90°,
∴OD⊥AB,
∵DE为⊙O的切线,
∴OD⊥DE,
∴AB∥DE;
(2)解:在Rt△ABC中,∵AB=10,AC=6,
∴BC8,
∵AB为直径,
∴∠BDA=90°,
∵∠DBA=∠ACD=45°,
∴△ABD为等腰直角三角形,
∴BD=ADAB=5,
∵AB∥DE,
∴∠E=∠ABC,∠EDB=∠DBA=45°,
而∠ABC=∠ADC,
∴∠E=∠ADC,
∵∠ACD=∠EDB=45°,
∴△EDB∽△DCA,
∴BE:AD=BD:AC,
即BE:55:6,
解得BE,
∴CE=BE+BC8,
∵∠EDB=∠ECD,∠DEB=∠CED,
∴△EDB∽△ECD,
∴DE:EC=BE:DE,
即DE::DE,
解得DE.
17.(2025 洪山区模拟)如图,在矩形ABCD中,点O是对角线AC和BD的交点,E为线段OB上一点,F为线段OD上一点,连接AE,CE,FC,AF.若 OE:OB=1:3,FD:OD=2:3 ,则四边形AECF是平行四边形.请从①AE⊥BD,CF⊥BD;②AE=CF;③OE:OB=1:3,FD:OD=2:3这三个选项中选择一个作为条件,使结论成立,并说明理由.
【解答】解:选择③OE:OB=1:3,FD:OD=2:3,
理由:∵四边形ABCD是矩形,对角线AC、BD交于点O,
∴OA=OC,OB=OD,
∴OBOD,
∵OE:OB=1:3,FD:OD=2:3,
∴OEOB,FDOD,
∴OF=ODODOD,
∴OE=OF,
∵OA=OC,OE=OF,
∴四边形AECF是平行四边形,
故答案为:OE:OB=1:3,FD:OD=2:3.
注:答案不唯一.
18.(2025 上城区二模)已知:如图,在△ABC中,AB=AC,D,E分别为BC,AB中点,连结DE并延长,使DE=EF.
(1)求证:四边形ADBF为矩形;
(2)记∠ADE=α,∠AEM=β.
①求∠DEM(用含α,β的代数式表示);
②若β=90°﹣2α,求证:2DE2=DM DA.
【解答】(1)证明:∵AB=AC,点D为BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∵点E为AB的中点,
∴DE=BE=AE,
∵DE=EF,
∴DE=EF=BE=AE,
∴四边形ADBF为矩形;
(2)①解:∵EA=ED,
∴∠EAD=∠ADE=α,
∴∠AED=180°﹣2α,
∴∠DEM=∠AED﹣∠AEM=180°﹣2α﹣β;
②证明:∵β=90°﹣2α,
∴∠DEM=180°﹣2α﹣β=180°﹣2α﹣(90°﹣2α)=90°,
∵四边形ADBF为矩形,
∴∠DAF=90°,
∵∠MDE=∠FDA,∠DEM=∠DAF,
∴△DEM∽△DAF,
∴DE:DA=DM:DF,
∴DE DF=DM DA,
而DF=2DE,
∴2DE2=DM DA.
19.(2025 南岸区模拟)如图,在△ABC中,D是AC边上一点,且AD=AB.AE平分∠BAC,交BC于点F,DE∥AB,DE交BC于点G.DH平分∠CDE,交BC于点H.
(1)求证:DH∥AE;
(2)如图2,当EG=GD,∠DHG=45°时,用等式表示AC与BC之间的数量关系,并证明;
(3)当∠BAD=60°时,连接EH,若△DEH为直角三角形,直接写出的值.
【解答】(1)证明:∵DE∥AB,
∴∠CAB=∠CDE,
又∵AE平分∠BAC,DH平分∠CDE,
∴,∠EDH=∠CDH,
∴∠CAE=∠CDH,
∴DH∥AE;
(2)解:,证明如下:
连接BD交AE于点O,连接BE,如图,
∵DE∥AB,
∴∠DEA=∠EAB,
又∵∠BAE=∠CAE,
∴∠DEA=∠CAE,
∴DE=DA=AB,
∴四边形ABED是菱形,
∴∠BOF=90°,BO=OD,BE∥AC,BE=AD,
∴∠BED=∠EDC,∠EBC=∠C,
又∵EG=GD,
∴△GEB≌△GDC(ASA),
∴BE=CD,BG=GC,
同理可得△GEF≌△GDH(ASA),
∴FG=GH,
设EO=OD=a,
∵DH∥AE,
∴∠BFO=∠GHD=45°,∠BOF=∠BDH=90°,
∴BO=OF=a,BD=DH=2OB=2a,
∴BFa,,
∴,
∴,
∴,
即,
又∵DH∥AE,
∴△CDH∽△CAF,
∴,
即AF=2DH=4a,
∴AO=AF﹣OF=4a﹣a=3a,
∴,
∴,
∴;
(3)解:∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
连BD交AE于M,如图,
由(2)可得:∠BAF=∠FAD=∠AED=30°,∠BMF=∠BDH=90°,BO=OD,
①当∠DHE=90°时,四边形DMEH是矩形,
∴DM=EH,DE=2DM=2EH,HE∥DM,
∴∠EHG=∠GBD,∠HEG=∠GDB,
∴△EHG∽△DBG,
∴,
∴DGDEEH,
∴;
②当∠HED=90°时,ED=2DM,
∴,
又∵DH∥AE,
∴∠HDE=∠MCD=30°,
∴,
∴,
又∵AE∥DH,
∴△BMF∽△BDH,
∴,
即,
∴,
又∵AE∥DH,
∴∠FEG=∠GDH,∠EFG=∠GHD,
∴△GEF∽△GDH,
∴,
∴,
∴;
综上,△DEH为直角三角形时,的值为或.
20.(2025 淮安区模拟)【初步感知】如图1,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B时,求证:.
【探索发现】如图2,在△ABC中,∠ABC=50°,AB=4,BC=3,点F是CB延长线上的一点,且BF=BC,在FC下方作∠CFG=∠ABC,将射线CA绕点C逆时针旋转130°,交射线FG于点G,求FG的长.
【尝试应用】如图3,在△ABC中,∠A>∠C,E为AC边上一点,连接BE,∠ABE=∠C,tanC,且,求的值.
【拓展提升】如图4,已知在菱形ABCD中,∠A=60°,点E在边AB上,且AE=mEB,连结CE交对角线BD于F,点G在线段CF上,连结DG,GB,若∠DGB=120°,GB=n,则DG= n .(用含有m、n的式子表示)
【解答】【初步感知】证明:∵∠DPC=∠A=∠B,∠APD+∠ADP=180°﹣∠A,∠APD+∠BPC=180°﹣∠DPC,
∴∠ADP=∠PBC,
∴△APD∽△BCP,
∴;
【探索发现】解:∵∠ABC=50°,
∴∠A+∠ACB=130°,
∵射线CA绕点C逆时针旋转130°,交射线FG于点G,
∴∠ACG=130°,
∴∠ACB+∠FCG=130°,
∴∠A=∠FCG,
∵∠CFG=∠ABC,
∴△ABC∽△CFG,
∴,
∵BF=BC=3,
∴CF=6,
∴,
∴FG;
【尝试应用】解:如图1,
作AD⊥BC于D,
设CE=3a,AE=7a,则AC=10a,
∵tanC,
∴sinC,cosC,
∴ADAC=8a,CDAC=6a,
∵∠ABE=∠C,∠BAC=∠BAE,
∴△ABE∽△ACB,
∴,
∴AB2=AE AC=70a2,
∴BD,
∴BC=CD+BD=(6)a,
∴;
【拓展提升】解:如图2,
作GV∥BD,交CD于V,交BC于W,
∴△CGV∽△CFD,△CGW∽△CFB,
∴,
∵四边形ABCD是菱形,
∴CD∥AB,CD=AB=BC,∠BCD=∠A=60°,
∴△BEF∽△DCG,△BCD是等边三角形,
∴,∠CDB=∠CBD=60°,
∴,∠DVG=∠BWG=120°,CV=CW,
∴∠WBG+∠BGW=60°,DV=BW,
∵∠DGB=120°,
∴∠BGW+∠DGV=60°,
∴∠DGV=∠WBG,
∴△DGV∽△GBW,
∴,
设GW=x,GW=(m+1)x,
∴,
∴DV x,
∴,
∴DG,
故答案为:n.
21.(2025 广信区校级模拟)【综合与实践】
【课本再现】
人教版九年级上册数学教材第60页有一例题:点E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.由作图过程可以得出△ADE≌△ABE′.由此,老师进行了延伸拓展,与同学们一起探究.
【例题延伸】
(1)如图1,在正方形ABCD中,点E,F分别是边BC,CD上的动点,且∠EAF=45°,试判断BE,EF,DF之间的数量关系.小明把△ABE绕点A顺时针旋转90°得到△ADG,使AB与AD重合,试求BE,EF,DF之间有什么数量关系?并说明理由;
【类比探究】
(2)如图2,在矩形ABCD中,已知AB=6,BC=8,点F为边BC延长线上一点,连接DF,过点B作BH⊥DF于点H,交CD于点E.
①求的值;
②求cos∠EFC的值;
【拓展应用】
(3)如图3,在(2)的条件下,平移线段DF,使它经过BE的中点H,交AD于点M,交BC于点N,连接NE,若,请你求出MN的长.
【解答】解:(1)EF=BE+DF;理由如下:
∵△ADG是△ABE绕点A顺时针旋转90°得到的,
∴∠ADG=∠B,AG=AE,∠DAG=∠BAE.
∵四边形ABCD是正方形,
∴∠B=∠BAD=∠ADC=90°,AB=AD,
∴∠ADG=90°,
∴∠ADG+∠ADC=180°,
∴C,D,G三点共线.
∵∠EAF=45°,∠BAD=90°,
∴∠BAE+∠DAF=45°,
∴∠DAG+∠DAF=45°,
∴∠GAF=45°,
∴∠GAF=∠EAF.
在△EAF和△GAF中,
,
∴△EAF≌△GAF(SAS),
∴EF=FG=DG+DF=BE+DF;
(2)①∵BE⊥DF,
∴∠CBE+∠DFC=90°.
在矩形ABCD中,∠DCF=∠DCB=90°,AB=CD,
∴∠CBE+∠BEC=90°,
∴∠BEC=∠DFC,
∴△BCE∽△DCF,
∴.
∵,
∴;
②∵△BCE∽△DCF,,
∴.
设CE=4a,则CF=3a,
在直角三角形CEF中,由勾股定理得:,
∴;
(3)由平移的性质可得MN∥DF,MN=DF.
∵点H为BE的中点,
∴MN垂直平分BE,
∴BN=NE.
∵,
∴设BN=EN=5x,CE=4x,
在直角三角形CEN中,由勾股定理得:,
∴BC=BN+CN=8x.
∵BC=8,
∴8x=8,
解得x=1,
∴CE=4.
∵,设MN=3y,
∴BE=4y.
在Rt△EBC中,由勾股定理得:BE2=BC2+CE2,
∴(4y)2=42+82,
解得或(不合题意,舍去),
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
