【中考模拟题汇编】查漏补缺:反比例函数-2025年中考数学(含答案)
文档属性
| 名称 | 【中考模拟题汇编】查漏补缺:反比例函数-2025年中考数学(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 05:41:49 | ||
图片预览


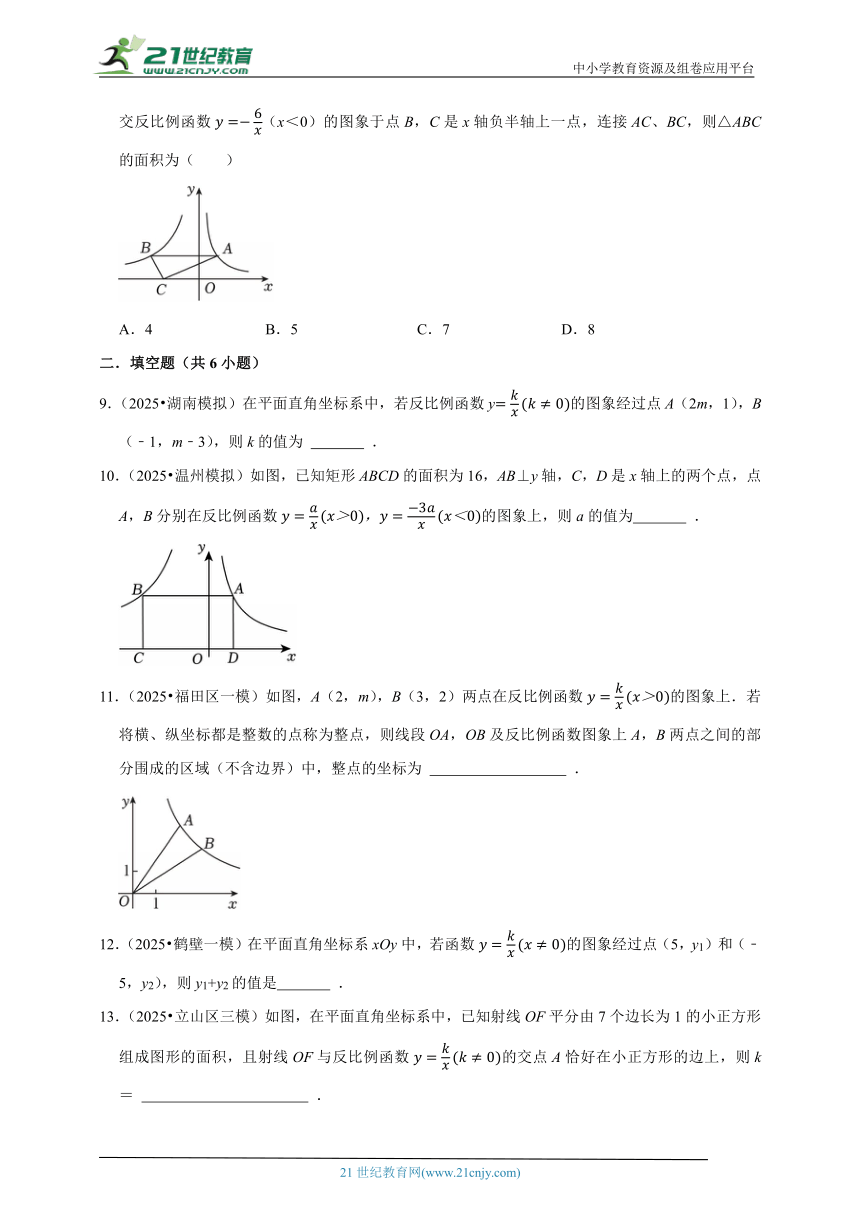

文档简介
中小学教育资源及组卷应用平台
【中考模拟题汇编】查漏补缺:反比例函数-2025年中考数学
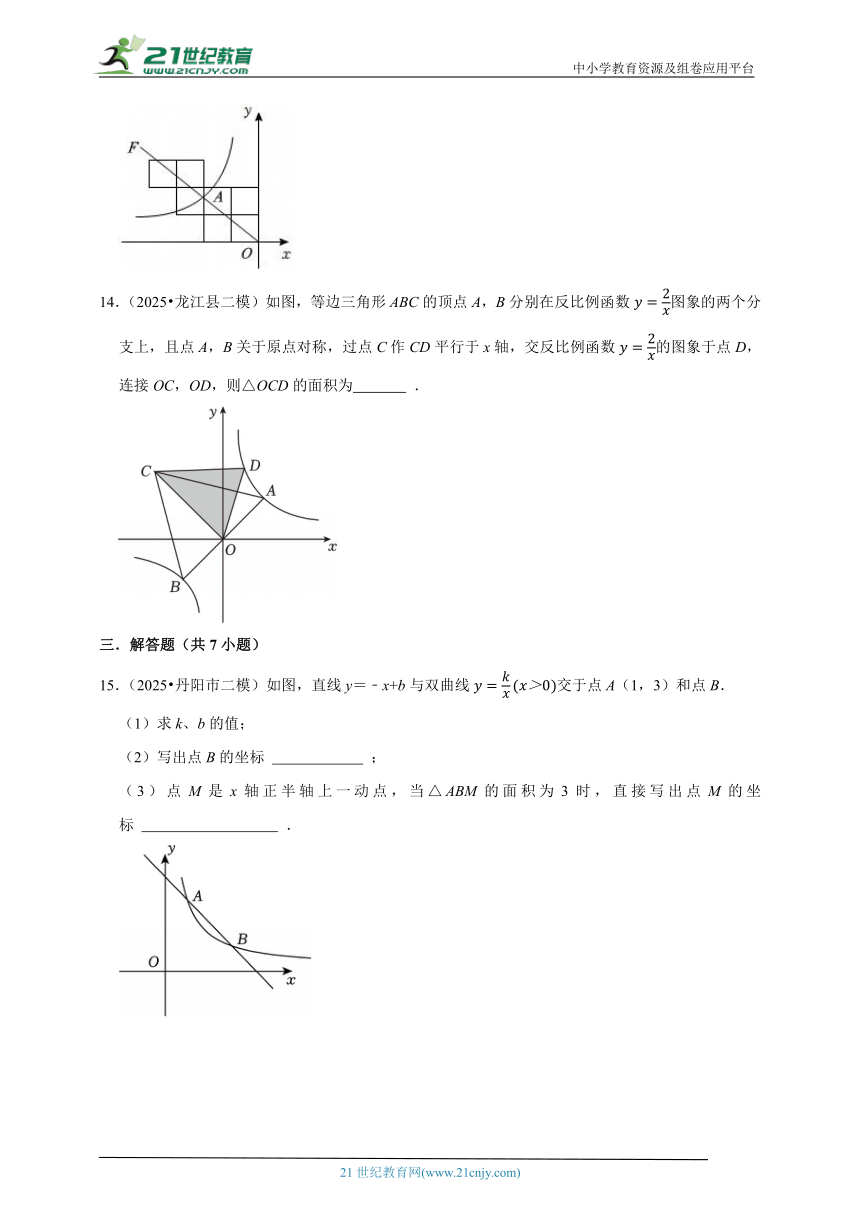
一.选择题(共8小题)
1.(2025 西山区二模)反比例函数的图象经过( )
A.第二、四象限 B.第一、三象限
C.第一、二象限 D.第三、四象限
2.(2025 绥化一模)若点(﹣2,y1)、(﹣1,y2)、(1,y3)都在反比例函数(k<0)的图象上,则有( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
3.(2025 南岸区模拟)物理兴趣小组在实验室研究电学时设计了一个电路,其电路图如图1所示.经测试,发现电流I(A)随着电阻R(Ω)的变化而变化,,并结合实验数据描点、连线,画成了如图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最小电流是9A B.最大电流是9A
C.最小电流是18A D.最大电流是18A
4.(2025 道里区二模)反比例函数的图象,当x>0时,y随x的增大而增大,则k的取值范围是( )
A.k>3 B.k≤3 C.k<3 D.k≥3
5.(2025 杭州模拟)综合实践小组的同学利用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(cm)是液体的密度ρ(g/cm3)的反比例函数,其图象如图所示(ρ>0).下列说法正确的是( )
A.当液体密度ρ≥1g/cm3时,浸在液体中的高度h≥20cm
B.当液体密度ρ=2g/cm3时,浸在液体中的高度h=40cm
C.当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3
D.当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≤20cm
6.(2025 岳麓区校级模拟)如图,正方形ABCD的顶点B在x轴上,点A,点C在反比例函数图象上.若直线BC交y轴负半轴于点G,且tan∠OGB=2,则直线BC的函数表达式为( )
A.y=2x﹣4 B. C. D.
7.(2025 云岩区一模)如图,在平面直角坐标系中,点在反比例函数y(k为常数,x<0)的图象上.将直线OA沿y轴向上平移后的直线与y轴交于点B,与此反比例函数的图象交于点C.若BC,则点B的坐标是( )
A. B.(0,4) C. D.(0,3)
8.(2025 碧江区 模拟)如图,在反比例函数的图象上任取一点A,过点A作AB∥x轴交反比例函数(x<0)的图象于点B,C是x轴负半轴上一点,连接AC、BC,则△ABC的面积为( )
A.4 B.5 C.7 D.8
二.填空题(共6小题)
9.(2025 湖南模拟)在平面直角坐标系中,若反比例函数y的图象经过点A(2m,1),B(﹣1,m﹣3),则k的值为 .
10.(2025 温州模拟)如图,已知矩形ABCD的面积为16,AB⊥y轴,C,D是x轴上的两个点,点A,B分别在反比例函数的图象上,则a的值为 .
11.(2025 福田区一模)如图,A(2,m),B(3,2)两点在反比例函数的图象上.若将横、纵坐标都是整数的点称为整点,则线段OA,OB及反比例函数图象上A,B两点之间的部分围成的区域(不含边界)中,整点的坐标为 .
12.(2025 鹤壁一模)在平面直角坐标系xOy中,若函数的图象经过点(5,y1)和(﹣5,y2),则y1+y2的值是 .
13.(2025 立山区三模)如图,在平面直角坐标系中,已知射线OF平分由7个边长为1的小正方形组成图形的面积,且射线OF与反比例函数的交点A恰好在小正方形的边上,则k= .
14.(2025 龙江县二模)如图,等边三角形ABC的顶点A,B分别在反比例函数图象的两个分支上,且点A,B关于原点对称,过点C作CD平行于x轴,交反比例函数的图象于点D,连接OC,OD,则△OCD的面积为 .
三.解答题(共7小题)
15.(2025 丹阳市二模)如图,直线y=﹣x+b与双曲线交于点A(1,3)和点B.
(1)求k、b的值;
(2)写出点B的坐标 ;
(3)点M是x轴正半轴上一动点,当△ABM的面积为3时,直接写出点M的坐标 .
16.(2025 河南模拟)如图,在平面直角坐标系中,已知一次函数y1=kx+b(k≠0)的图象与反比例函数的图象交于A,B两点,已知点A(1,4),点B的横坐标为﹣2.
(1)求一次函数与反比例函数的解析式;
(2)D为x轴上一点,若△ABD的面积为6,求点D的坐标;
(3)根据函数图象,直接写出不等式y1≤y2的解集.
17.(2025 西市区校级模拟)国家规定,如果驾驶人员血液中每100毫升的酒精含量大于或等于20毫克且小于80毫克,则被认定为饮酒后驾车,如果每100毫升的血液中酒精含量大于或等于80毫克,则被认定为醉酒后驾车,且此时肝部正被严重损伤,一般成人饮用低度白酒0.25kg后,血液中酒精含量y(单位:毫克/百毫升)与时间x(单位:时)的关系可近似地用如图所示的图象表示.
(1)求OA所在直线及部分双曲线BC的函数表达式(不用写x的取值范围).
(2)饮用低度白酒0.25kg后,肝部被严重损伤会持续多少时间?
(3)假设某驾驶员晚上20:00在家喝完0.25kg低度白酒,第二天早上7:00能否驾车去上班?请判断并说明理由.
18.(2025 涪城区三模)如图,一次函数y=kx+b(k≠0)的图象与反比例函数y(m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(1)求一次函数和反比例函数的解析式;
(2)若点E是点C关于x轴的对称点,求△ABE的面积.
19.(2025 碧江区 模拟)在初二物理的学习中,我们知道压强p(Pa),压力F(N),受力面积S(m2)满足公式.
(1)当F为定值时,如图所示的图象能够正确反映p与S之间函数关系的图象是 (填序号);
(2)已知一块比较薄的冰面最多承受10000Pa的压强,小明的重量为600N.
①若小明的一双鞋底与冰面的接触面积共0.03m2,他能否安全地站在这块冰面上?
②若小明平躺在冰面上的一块质量不计的薄木板上,为了保证安全,这块薄木板的面积应满足什么条件?
20.(2025 越秀区校级二模)综合与实践:课题小空间检测视力问题
具体情境:对某班学生视力进行检测的任务:
现有条件:一张测试距离为5米的视力表,一间长为3.8米,宽为3.6米的空书房.
(1)如图1,若将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理可知:测试线应画在距离墙ABEF 米处;
(2)小明选择按比例制作视力表完成该任务,在制作过程中发现视力表上视力值V和该行字母E的宽度a之间的关系是一种函数模型,字母E的宽度a如图2所示,视力表上部分视力值V和字母E的宽度a的部分对应数据如所示:
位置 视力值V a的值(mm)
第1行 0.1 70
第5行 0.25 28
第8行 0.5 14
第14行 2 3.5
①根据表格数据判断,从一次函数、反比例函数中选择一个合适的函数模型拟合视力值V与字母E的宽度a(说明理由),并求出视力值V与字母E宽度a之间的函数关系式;
②小明在制作过程中发现某行字母E的宽度a的值17.5mm,请问该行对应的视力值是多少?
21.(2025 青白江区模拟)如图1,已知点(a,b)为双曲线上一点,且,直线y=﹣x+t分别交x、y轴及双曲线于点A、B、C.
(1)求双曲线的解析式;
(2)如图2,连接OC.
①若t=8,在双曲线上找一点D,使得△OBD的面积是△OBC的面积的3倍,请求出此时点D的坐标;
②当t的值变化时,的值是否发生变化?若不变,求出它的值;若变化,请说明理由.
【中考模拟题汇编】查漏补缺:反比例函数-2025年中考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A C D C C C D A
一.选择题(共8小题)
1.(2025 西山区二模)反比例函数的图象经过( )
A.第二、四象限 B.第一、三象限
C.第一、二象限 D.第三、四象限
【解答】解:反比例函数中,
∵k=﹣3<0,
∴此函数图象的两个分支分别位于第二、四象限.
故选:A.
2.(2025 绥化一模)若点(﹣2,y1)、(﹣1,y2)、(1,y3)都在反比例函数(k<0)的图象上,则有( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
【解答】解:∵反比例函数y中k<0,
∴函数图象的两个分支位于二四象限,且在每一象限内y随x的增大而增大,
∵﹣2<﹣1<0,
∴y2>y1>0,
∵1>0,
∴y3<0,
∴y2>y1>y3.
故选:C.
3.(2025 南岸区模拟)物理兴趣小组在实验室研究电学时设计了一个电路,其电路图如图1所示.经测试,发现电流I(A)随着电阻R(Ω)的变化而变化,,并结合实验数据描点、连线,画成了如图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最小电流是9A B.最大电流是9A
C.最小电流是18A D.最大电流是18A
【解答】解:电流I(A)随着电阻R(Ω)的变化而变化,,
电流与电阻成反比例关系,
由图象可得:过(3,6)‘
∴U=18.
当电阻最小时,电流最大,
该电路的最小电阻为1Ω,则该电路能通过的最大电流为:I18.
故选:D.
4.(2025 道里区二模)反比例函数的图象,当x>0时,y随x的增大而增大,则k的取值范围是( )
A.k>3 B.k≤3 C.k<3 D.k≥3
【解答】解:∵当x>0时,y随x的增大而增大,
∴函数图象必在第四象限,
∴k﹣3<0,
∴k<3.
故选:C.
5.(2025 杭州模拟)综合实践小组的同学利用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(cm)是液体的密度ρ(g/cm3)的反比例函数,其图象如图所示(ρ>0).下列说法正确的是( )
A.当液体密度ρ≥1g/cm3时,浸在液体中的高度h≥20cm
B.当液体密度ρ=2g/cm3时,浸在液体中的高度h=40cm
C.当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3
D.当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≤20cm
【解答】解:根据题意得,反比例函数解析式为:h,
A、当液体密度ρ≥1g/cm3时,浸在液体中的高度h≤20cm,故原说法错误,不符合题意;
B、当液体密度ρ=2g/cm3时,浸在液体中的高度h=10cm,故原说法错误,不符合题意;,
C、当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3,正确,符合题意;
D、当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≥20cm,故原说法错误,不符合题意;,
故选:C.
6.(2025 岳麓区校级模拟)如图,正方形ABCD的顶点B在x轴上,点A,点C在反比例函数图象上.若直线BC交y轴负半轴于点G,且tan∠OGB=2,则直线BC的函数表达式为( )
A.y=2x﹣4 B. C. D.
【解答】解:过A作AE⊥x轴于E,过C作CF⊥x轴于F,
在Rt△BOG中,tan∠OGB2,
∴设OB=2m,OG=m(m>0),
∵∠BOG=∠BFC=90°,∠OBG=∠CBF,
∴△OBG∽△FBC,
∴2,
∴设BF=2n,CF=n(n>0),
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠EAB+∠ABE=∠ABE+∠CBF=90°,
∴∠EAB=∠CBF,
在△AEB与△BFC中,
,
∴△AEB≌△BFC(AAS),
∴AE=BF=2n,BE=CF=n,
∴OF=OB+BF=2m+2n,OE=OB﹣BE=2m﹣n,
∴C(2m+2n,n),A(2m﹣n,2n),
∵点A,点C在反比例函数y(k>0,x>0)图象上,
∴,
解得或(舍去),
∴G(0﹣4),B(8,0),
设直线BC的解析式为y=kx+b,
把B,G坐标代入解析式得:,
解得,
∴直线BC的解析式为yx﹣4,
故选:C.
7.(2025 云岩区一模)如图,在平面直角坐标系中,点在反比例函数y(k为常数,x<0)的图象上.将直线OA沿y轴向上平移后的直线与y轴交于点B,与此反比例函数的图象交于点C.若BC,则点B的坐标是( )
A. B.(0,4) C. D.(0,3)
【解答】解:由题意,∵点A(﹣2,2)在函数y上,
∴k=﹣22=﹣4.
∴反比例函数为y.
设直线OA为y=ax,
∴﹣2a=2.
∴a.
∴直线OA为yx.
又设向上平移m个单位到直线BC,
∴B(0,m),直线BC为yx+m.
再设C(c,)(c<0),
∴c+m.
∴mc.
作CH⊥y轴于H,
∴CH=c,BHmc,BH2+CH2=BC2.
∴c2+c2=3.
∴c.
∴4﹣m=1.
∴m=3.
∴B(0,3).
故选:D.
8.(2025 碧江区 模拟)如图,在反比例函数的图象上任取一点A,过点A作AB∥x轴交反比例函数(x<0)的图象于点B,C是x轴负半轴上一点,连接AC、BC,则△ABC的面积为( )
A.4 B.5 C.7 D.8
【解答】解:如图,连接OA、OB,线段AB交y轴于点D,
∵点A在反比例函数y图象上,点B在反比例函数y图象上,
∴S△AOD=1,S△BOD=3,
∴S△AOB=4,
∵AB∥x轴,
∴S△ABC=S△AOB=4.
故选:A.
二.填空题(共6小题)
9.(2025 湖南模拟)在平面直角坐标系中,若反比例函数y的图象经过点A(2m,1),B(﹣1,m﹣3),则k的值为 2 .
【解答】解:∵反比例函数y的图象经过点A(2m,1),B(﹣1,m﹣3),
∴2m×1=﹣1×(m﹣3),
解得:m=1,
∴A (2,1),
∴k=2.
故答案为:2.
10.(2025 温州模拟)如图,已知矩形ABCD的面积为16,AB⊥y轴,C,D是x轴上的两个点,点A,B分别在反比例函数的图象上,则a的值为 4 .
【解答】解:设点A坐标为(m,)(m>0,a>0),
∵AB⊥y轴,
∴点B坐标为(﹣3m,),
∴m |﹣3m| a+3a=16,
解得a=4,
故答案为:4.
11.(2025 福田区一模)如图,A(2,m),B(3,2)两点在反比例函数的图象上.若将横、纵坐标都是整数的点称为整点,则线段OA,OB及反比例函数图象上A,B两点之间的部分围成的区域(不含边界)中,整点的坐标为 (1,1)和(2,2) .
【解答】解:∵A(2,m),B(3,2)两点在反比例函数的图象上,
∴k=2m=3×2,
∴k=6,m=3,
∴反比例函数为y,A(2,3),
∵A(2,3),B(3,2),
∴直线OA为y1x,OB为y2x,
当x=1时,y1,y2,
当x=2时,y2,
∴线段OA,OB及反比例函数图象上A,B两点之间的部分围成的区域(不含边界)中整点有(1,1),(2,2).
故答案为:(1,1)和(2,2).
12.(2025 鹤壁一模)在平面直角坐标系xOy中,若函数的图象经过点(5,y1)和(﹣5,y2),则y1+y2的值是 0 .
【解答】解:∵函数的图象经过点(5,y1)和(﹣5,y2),
∴,,
∴,
故答案为:0.
13.(2025 立山区三模)如图,在平面直角坐标系中,已知射线OF平分由7个边长为1的小正方形组成图形的面积,且射线OF与反比例函数的交点A恰好在小正方形的边上,则k= .
【解答】解:如图,由图可知,点A的横坐标为﹣2,点H的纵坐标为3,
∵点A在反比例函数的图象上,
∴,A(﹣2,),
设直线OF的解析式为y=mx,由条件可得,
解得,
∴直线OF的解析式为,
把点H的纵坐标为3代入得到,
解得,
∴,
∴,
由条件可得,
解得,
经检验,是分式方程的解且符合题意.
故答案为:.
14.(2025 龙江县二模)如图,等边三角形ABC的顶点A,B分别在反比例函数图象的两个分支上,且点A,B关于原点对称,过点C作CD平行于x轴,交反比例函数的图象于点D,连接OC,OD,则△OCD的面积为 4 .
【解答】解:如图,过C、A作CM⊥x轴,AN⊥x轴于M、N,令CD交y轴于点H,则四边形CMOH是矩形,
∴∠CHO=∠DHO=90°,∠CMO=∠ONA=90°,S△COM=S△COH,
由对称可知OA=OB,OC⊥AB,
∴∠AOC=90°,
∵△ABC是等边三角形,
∴∠ACB=∠BAC=60°,
∴,
∵∠AOC=90°,AN⊥x轴,
∴∠OAN=90°﹣∠AON=∠COM,
∴△COM∽△OAN,
∴,
∴,
∴S△COH=S△COM=3S△OAN=3,
∴△OCD的面积为S△COM+S△ODH=3+1=4,
故答案为:4.
三.解答题(共7小题)
15.(2025 丹阳市二模)如图,直线y=﹣x+b与双曲线交于点A(1,3)和点B.
(1)求k、b的值;
(2)写出点B的坐标 (3,1) ;
(3)点M是x轴正半轴上一动点,当△ABM的面积为3时,直接写出点M的坐标 (1,0)或(7,0) .
【解答】解:(1)∵直线y=﹣x+b与双曲线交于点A(1,3),
∴3=﹣1+b,3,
∴k=3,b=4;
(2)解方程组,得或,
∴B(3,1).
故答案为:(3,1);
(3)令y=0,则y=﹣x+4=0,解得x=4,
∴C(4,0),
∵S△AMB=3,
∴S△AMB=S△AMC﹣S△BMC3,
∴MC=3,
∴M(1,0)或(7,0).
故答案为:(1,0)或(7,0).
16.(2025 河南模拟)如图,在平面直角坐标系中,已知一次函数y1=kx+b(k≠0)的图象与反比例函数的图象交于A,B两点,已知点A(1,4),点B的横坐标为﹣2.
(1)求一次函数与反比例函数的解析式;
(2)D为x轴上一点,若△ABD的面积为6,求点D的坐标;
(3)根据函数图象,直接写出不等式y1≤y2的解集.
【解答】解:(1)将A(1,4)代入y2得a=4,
∴反比例函数的解析式为y2,
将x=﹣2代入y2得y2=﹣2,
∴点B坐标为(﹣2,﹣2),
将A(1,4)B(﹣2,﹣2)代入y1=kx+b得
,解的,
∴y1=2x+2.
(2)设直线与x轴交点为C,将y=0代入y1=2x+2得x=﹣1
∴直线AB与x轴交点C的坐标为(﹣1,0),
设D点坐标为(n,0),
则S△ABD=S△ACD+S△BCDCD yACD |yB||﹣1﹣n|×4|﹣1﹣n|×2=3|﹣1﹣n|=6,
∴﹣1﹣n=2或﹣1﹣n=﹣2,解得n=﹣3或n=1,
∴点D坐标为(﹣3,0)或(1,0);
(3)由图象可得x≤﹣2或0<x≤1时,y1≤y2.
17.(2025 西市区校级模拟)国家规定,如果驾驶人员血液中每100毫升的酒精含量大于或等于20毫克且小于80毫克,则被认定为饮酒后驾车,如果每100毫升的血液中酒精含量大于或等于80毫克,则被认定为醉酒后驾车,且此时肝部正被严重损伤,一般成人饮用低度白酒0.25kg后,血液中酒精含量y(单位:毫克/百毫升)与时间x(单位:时)的关系可近似地用如图所示的图象表示.
(1)求OA所在直线及部分双曲线BC的函数表达式(不用写x的取值范围).
(2)饮用低度白酒0.25kg后,肝部被严重损伤会持续多少时间?
(3)假设某驾驶员晚上20:00在家喝完0.25kg低度白酒,第二天早上7:00能否驾车去上班?请判断并说明理由.
【解答】解:(1)设OA的函数表达式为y=kx,则:x=120,
∴k=100,
∴OA的函数表达式为y=100x,
可设部分双曲线BC的函数表达式为y,
由图象可知,当x=2时,y=120,
∴m=240,
∴部分双曲线BC的函数表达式为y;
(2)由(1)知y;
∴y80时,x=3;
当y=100x=80时,x=0.8,
∴饮用低度白酒0.25kg后,肝部被严重损伤会持续3﹣0.8=2.2小时.
(3)在y中,令y<20,
可得:20,
解之可得:x>12,
∵晚上20:00到第二天早上7:00的时间间隔为7+4=11(h),11h<12h,
∴某人晚上20:00喝完完0.25kg白酒,则此人第二天早上7:00时体内的酒精含量高于20(毫克/百毫升),
∴某人晚上20:00喝完完0.25kg低度白酒,则此人第二天早上7:00不能驾车出行.
18.(2025 涪城区三模)如图,一次函数y=kx+b(k≠0)的图象与反比例函数y(m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(1)求一次函数和反比例函数的解析式;
(2)若点E是点C关于x轴的对称点,求△ABE的面积.
【解答】解:(1)∵AD⊥x轴于点D,
∴AD∥y轴,
设A(a,2),
∴AD=2,
∵∠CAD=45°,
∴∠AFD=45°,
∴FD=AD=2,
连接AO,
∵AD∥y轴,
∴S△AOD=S△ADC=6,
∴OD=6,
∴A(6,2),
将A(6,2)代入,得m=12,
∴反比例函数解析式为y;
∵∠OCF=∠CAD=45°,
在△COF中,OC=OF=OD﹣FD=6﹣2=4,
∴C(0,﹣4),
将点A(6,2),点C(0,﹣4)代入y=kx+b,可得
,
∴,
∴一次函数解析式为y=x﹣4;
(2)点E是点C关于x轴的对称点,
∴E(0,4),
∴CE=8,
解方程组,
得 或,
∴B(﹣2,﹣6),
∴.
19.(2025 碧江区 模拟)在初二物理的学习中,我们知道压强p(Pa),压力F(N),受力面积S(m2)满足公式.
(1)当F为定值时,如图所示的图象能够正确反映p与S之间函数关系的图象是 ① (填序号);
(2)已知一块比较薄的冰面最多承受10000Pa的压强,小明的重量为600N.
①若小明的一双鞋底与冰面的接触面积共0.03m2,他能否安全地站在这块冰面上?
②若小明平躺在冰面上的一块质量不计的薄木板上,为了保证安全,这块薄木板的面积应满足什么条件?
【解答】解:(1)F为定值时,p与S之间是反比例函数的关系,且p随S的增大而减小,
∴p与S之间函数关系的图象是①.
故答案为:①.
(2)①当F=600,S=0.03时,p20000,
∵20000>10000,
∴他不能否安全地站在这块冰面上.
②根据题意,得10000,
解得S≥0.06.
答:这块薄木板的面积不能小于0.06m2.
20.(2025 越秀区校级二模)综合与实践:课题小空间检测视力问题
具体情境:对某班学生视力进行检测的任务:
现有条件:一张测试距离为5米的视力表,一间长为3.8米,宽为3.6米的空书房.
(1)如图1,若将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理可知:测试线应画在距离墙ABEF 1.2 米处;
(2)小明选择按比例制作视力表完成该任务,在制作过程中发现视力表上视力值V和该行字母E的宽度a之间的关系是一种函数模型,字母E的宽度a如图2所示,视力表上部分视力值V和字母E的宽度a的部分对应数据如所示:
位置 视力值V a的值(mm)
第1行 0.1 70
第5行 0.25 28
第8行 0.5 14
第14行 2 3.5
①根据表格数据判断,从一次函数、反比例函数中选择一个合适的函数模型拟合视力值V与字母E的宽度a(说明理由),并求出视力值V与字母E宽度a之间的函数关系式;
②小明在制作过程中发现某行字母E的宽度a的值17.5mm,请问该行对应的视力值是多少?
【解答】解:(1)5﹣3.8=1.2(米),
∴测试线应画在距离墙ABEF1.2米处,
故答案为:1.2.
(2)①∵视力值V与字母宽度a的乘积是定值7,
∴视力值V与字母宽度a成反比例函数关系.
设V,
把a=70,V=0.1,代入得到k=7,
∴视力值V与字母宽度a的函数关系是V.
②把a=17.5,代入V,得V=0.4,
∴该行对应的视力值是0.4.
21.(2025 青白江区模拟)如图1,已知点(a,b)为双曲线上一点,且,直线y=﹣x+t分别交x、y轴及双曲线于点A、B、C.
(1)求双曲线的解析式;
(2)如图2,连接OC.
①若t=8,在双曲线上找一点D,使得△OBD的面积是△OBC的面积的3倍,请求出此时点D的坐标;
②当t的值变化时,的值是否发生变化?若不变,求出它的值;若变化,请说明理由.
【解答】解:(1)∵,
∴,
∴.
∴a=﹣3,b=3.
∴k=﹣3×3=﹣9.
∴双曲线的解析式.
(2)①由题意,当t=8时,y=﹣x+8,令x=0,得y=8,
∴B(0,8),即OB=8.
令y=0,得﹣x+8=0,即x=8,
∴A(8,0),即OA=8,
又联立方程﹣x+8,
∴x=﹣1或x=9(x<0).
∴C(﹣1,9).
∴S△BOCOB |xC|8×1=4.
设点D的坐标为(m,﹣m),m<0,
∴.
∵S△DOB=3S△BOC=12
∴﹣4m=12.
∴m=﹣3.
∴D(﹣3,3).
②的值不发生变化,理由如下:过C作CH⊥y轴于H,
如图:在y=﹣x+t中,令x=0得y=t,令y=0得x=t,
∴OA=OB=t,
∴AB2=OA2+OB2=2OA2,.
∴△AOB是等腰直角三角形,∠ABO=45°=∠CBH.
∴△CBH是等腰直角三角形.
∴CH=BH.
设CH=BH=x,则OH=t+x,
∴OC2=OH2+CH2=(t+x)2+x2,
∴OC2﹣OA2=(t+x)2+x2﹣t2=2x(x+t),
由反比例函数可得,,
∴CH﹣OH=9,即x(x+t)=9,
∴OC2﹣OA2=2x(x+t)=18.
∴18,即的值不发生变化,为18.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【中考模拟题汇编】查漏补缺:反比例函数-2025年中考数学
一.选择题(共8小题)
1.(2025 西山区二模)反比例函数的图象经过( )
A.第二、四象限 B.第一、三象限
C.第一、二象限 D.第三、四象限
2.(2025 绥化一模)若点(﹣2,y1)、(﹣1,y2)、(1,y3)都在反比例函数(k<0)的图象上,则有( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
3.(2025 南岸区模拟)物理兴趣小组在实验室研究电学时设计了一个电路,其电路图如图1所示.经测试,发现电流I(A)随着电阻R(Ω)的变化而变化,,并结合实验数据描点、连线,画成了如图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最小电流是9A B.最大电流是9A
C.最小电流是18A D.最大电流是18A
4.(2025 道里区二模)反比例函数的图象,当x>0时,y随x的增大而增大,则k的取值范围是( )
A.k>3 B.k≤3 C.k<3 D.k≥3
5.(2025 杭州模拟)综合实践小组的同学利用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(cm)是液体的密度ρ(g/cm3)的反比例函数,其图象如图所示(ρ>0).下列说法正确的是( )
A.当液体密度ρ≥1g/cm3时,浸在液体中的高度h≥20cm
B.当液体密度ρ=2g/cm3时,浸在液体中的高度h=40cm
C.当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3
D.当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≤20cm
6.(2025 岳麓区校级模拟)如图,正方形ABCD的顶点B在x轴上,点A,点C在反比例函数图象上.若直线BC交y轴负半轴于点G,且tan∠OGB=2,则直线BC的函数表达式为( )
A.y=2x﹣4 B. C. D.
7.(2025 云岩区一模)如图,在平面直角坐标系中,点在反比例函数y(k为常数,x<0)的图象上.将直线OA沿y轴向上平移后的直线与y轴交于点B,与此反比例函数的图象交于点C.若BC,则点B的坐标是( )
A. B.(0,4) C. D.(0,3)
8.(2025 碧江区 模拟)如图,在反比例函数的图象上任取一点A,过点A作AB∥x轴交反比例函数(x<0)的图象于点B,C是x轴负半轴上一点,连接AC、BC,则△ABC的面积为( )
A.4 B.5 C.7 D.8
二.填空题(共6小题)
9.(2025 湖南模拟)在平面直角坐标系中,若反比例函数y的图象经过点A(2m,1),B(﹣1,m﹣3),则k的值为 .
10.(2025 温州模拟)如图,已知矩形ABCD的面积为16,AB⊥y轴,C,D是x轴上的两个点,点A,B分别在反比例函数的图象上,则a的值为 .
11.(2025 福田区一模)如图,A(2,m),B(3,2)两点在反比例函数的图象上.若将横、纵坐标都是整数的点称为整点,则线段OA,OB及反比例函数图象上A,B两点之间的部分围成的区域(不含边界)中,整点的坐标为 .
12.(2025 鹤壁一模)在平面直角坐标系xOy中,若函数的图象经过点(5,y1)和(﹣5,y2),则y1+y2的值是 .
13.(2025 立山区三模)如图,在平面直角坐标系中,已知射线OF平分由7个边长为1的小正方形组成图形的面积,且射线OF与反比例函数的交点A恰好在小正方形的边上,则k= .
14.(2025 龙江县二模)如图,等边三角形ABC的顶点A,B分别在反比例函数图象的两个分支上,且点A,B关于原点对称,过点C作CD平行于x轴,交反比例函数的图象于点D,连接OC,OD,则△OCD的面积为 .
三.解答题(共7小题)
15.(2025 丹阳市二模)如图,直线y=﹣x+b与双曲线交于点A(1,3)和点B.
(1)求k、b的值;
(2)写出点B的坐标 ;
(3)点M是x轴正半轴上一动点,当△ABM的面积为3时,直接写出点M的坐标 .
16.(2025 河南模拟)如图,在平面直角坐标系中,已知一次函数y1=kx+b(k≠0)的图象与反比例函数的图象交于A,B两点,已知点A(1,4),点B的横坐标为﹣2.
(1)求一次函数与反比例函数的解析式;
(2)D为x轴上一点,若△ABD的面积为6,求点D的坐标;
(3)根据函数图象,直接写出不等式y1≤y2的解集.
17.(2025 西市区校级模拟)国家规定,如果驾驶人员血液中每100毫升的酒精含量大于或等于20毫克且小于80毫克,则被认定为饮酒后驾车,如果每100毫升的血液中酒精含量大于或等于80毫克,则被认定为醉酒后驾车,且此时肝部正被严重损伤,一般成人饮用低度白酒0.25kg后,血液中酒精含量y(单位:毫克/百毫升)与时间x(单位:时)的关系可近似地用如图所示的图象表示.
(1)求OA所在直线及部分双曲线BC的函数表达式(不用写x的取值范围).
(2)饮用低度白酒0.25kg后,肝部被严重损伤会持续多少时间?
(3)假设某驾驶员晚上20:00在家喝完0.25kg低度白酒,第二天早上7:00能否驾车去上班?请判断并说明理由.
18.(2025 涪城区三模)如图,一次函数y=kx+b(k≠0)的图象与反比例函数y(m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(1)求一次函数和反比例函数的解析式;
(2)若点E是点C关于x轴的对称点,求△ABE的面积.
19.(2025 碧江区 模拟)在初二物理的学习中,我们知道压强p(Pa),压力F(N),受力面积S(m2)满足公式.
(1)当F为定值时,如图所示的图象能够正确反映p与S之间函数关系的图象是 (填序号);
(2)已知一块比较薄的冰面最多承受10000Pa的压强,小明的重量为600N.
①若小明的一双鞋底与冰面的接触面积共0.03m2,他能否安全地站在这块冰面上?
②若小明平躺在冰面上的一块质量不计的薄木板上,为了保证安全,这块薄木板的面积应满足什么条件?
20.(2025 越秀区校级二模)综合与实践:课题小空间检测视力问题
具体情境:对某班学生视力进行检测的任务:
现有条件:一张测试距离为5米的视力表,一间长为3.8米,宽为3.6米的空书房.
(1)如图1,若将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理可知:测试线应画在距离墙ABEF 米处;
(2)小明选择按比例制作视力表完成该任务,在制作过程中发现视力表上视力值V和该行字母E的宽度a之间的关系是一种函数模型,字母E的宽度a如图2所示,视力表上部分视力值V和字母E的宽度a的部分对应数据如所示:
位置 视力值V a的值(mm)
第1行 0.1 70
第5行 0.25 28
第8行 0.5 14
第14行 2 3.5
①根据表格数据判断,从一次函数、反比例函数中选择一个合适的函数模型拟合视力值V与字母E的宽度a(说明理由),并求出视力值V与字母E宽度a之间的函数关系式;
②小明在制作过程中发现某行字母E的宽度a的值17.5mm,请问该行对应的视力值是多少?
21.(2025 青白江区模拟)如图1,已知点(a,b)为双曲线上一点,且,直线y=﹣x+t分别交x、y轴及双曲线于点A、B、C.
(1)求双曲线的解析式;
(2)如图2,连接OC.
①若t=8,在双曲线上找一点D,使得△OBD的面积是△OBC的面积的3倍,请求出此时点D的坐标;
②当t的值变化时,的值是否发生变化?若不变,求出它的值;若变化,请说明理由.
【中考模拟题汇编】查漏补缺:反比例函数-2025年中考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A C D C C C D A
一.选择题(共8小题)
1.(2025 西山区二模)反比例函数的图象经过( )
A.第二、四象限 B.第一、三象限
C.第一、二象限 D.第三、四象限
【解答】解:反比例函数中,
∵k=﹣3<0,
∴此函数图象的两个分支分别位于第二、四象限.
故选:A.
2.(2025 绥化一模)若点(﹣2,y1)、(﹣1,y2)、(1,y3)都在反比例函数(k<0)的图象上,则有( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
【解答】解:∵反比例函数y中k<0,
∴函数图象的两个分支位于二四象限,且在每一象限内y随x的增大而增大,
∵﹣2<﹣1<0,
∴y2>y1>0,
∵1>0,
∴y3<0,
∴y2>y1>y3.
故选:C.
3.(2025 南岸区模拟)物理兴趣小组在实验室研究电学时设计了一个电路,其电路图如图1所示.经测试,发现电流I(A)随着电阻R(Ω)的变化而变化,,并结合实验数据描点、连线,画成了如图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最小电流是9A B.最大电流是9A
C.最小电流是18A D.最大电流是18A
【解答】解:电流I(A)随着电阻R(Ω)的变化而变化,,
电流与电阻成反比例关系,
由图象可得:过(3,6)‘
∴U=18.
当电阻最小时,电流最大,
该电路的最小电阻为1Ω,则该电路能通过的最大电流为:I18.
故选:D.
4.(2025 道里区二模)反比例函数的图象,当x>0时,y随x的增大而增大,则k的取值范围是( )
A.k>3 B.k≤3 C.k<3 D.k≥3
【解答】解:∵当x>0时,y随x的增大而增大,
∴函数图象必在第四象限,
∴k﹣3<0,
∴k<3.
故选:C.
5.(2025 杭州模拟)综合实践小组的同学利用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(cm)是液体的密度ρ(g/cm3)的反比例函数,其图象如图所示(ρ>0).下列说法正确的是( )
A.当液体密度ρ≥1g/cm3时,浸在液体中的高度h≥20cm
B.当液体密度ρ=2g/cm3时,浸在液体中的高度h=40cm
C.当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3
D.当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≤20cm
【解答】解:根据题意得,反比例函数解析式为:h,
A、当液体密度ρ≥1g/cm3时,浸在液体中的高度h≤20cm,故原说法错误,不符合题意;
B、当液体密度ρ=2g/cm3时,浸在液体中的高度h=10cm,故原说法错误,不符合题意;,
C、当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3,正确,符合题意;
D、当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≥20cm,故原说法错误,不符合题意;,
故选:C.
6.(2025 岳麓区校级模拟)如图,正方形ABCD的顶点B在x轴上,点A,点C在反比例函数图象上.若直线BC交y轴负半轴于点G,且tan∠OGB=2,则直线BC的函数表达式为( )
A.y=2x﹣4 B. C. D.
【解答】解:过A作AE⊥x轴于E,过C作CF⊥x轴于F,
在Rt△BOG中,tan∠OGB2,
∴设OB=2m,OG=m(m>0),
∵∠BOG=∠BFC=90°,∠OBG=∠CBF,
∴△OBG∽△FBC,
∴2,
∴设BF=2n,CF=n(n>0),
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠EAB+∠ABE=∠ABE+∠CBF=90°,
∴∠EAB=∠CBF,
在△AEB与△BFC中,
,
∴△AEB≌△BFC(AAS),
∴AE=BF=2n,BE=CF=n,
∴OF=OB+BF=2m+2n,OE=OB﹣BE=2m﹣n,
∴C(2m+2n,n),A(2m﹣n,2n),
∵点A,点C在反比例函数y(k>0,x>0)图象上,
∴,
解得或(舍去),
∴G(0﹣4),B(8,0),
设直线BC的解析式为y=kx+b,
把B,G坐标代入解析式得:,
解得,
∴直线BC的解析式为yx﹣4,
故选:C.
7.(2025 云岩区一模)如图,在平面直角坐标系中,点在反比例函数y(k为常数,x<0)的图象上.将直线OA沿y轴向上平移后的直线与y轴交于点B,与此反比例函数的图象交于点C.若BC,则点B的坐标是( )
A. B.(0,4) C. D.(0,3)
【解答】解:由题意,∵点A(﹣2,2)在函数y上,
∴k=﹣22=﹣4.
∴反比例函数为y.
设直线OA为y=ax,
∴﹣2a=2.
∴a.
∴直线OA为yx.
又设向上平移m个单位到直线BC,
∴B(0,m),直线BC为yx+m.
再设C(c,)(c<0),
∴c+m.
∴mc.
作CH⊥y轴于H,
∴CH=c,BHmc,BH2+CH2=BC2.
∴c2+c2=3.
∴c.
∴4﹣m=1.
∴m=3.
∴B(0,3).
故选:D.
8.(2025 碧江区 模拟)如图,在反比例函数的图象上任取一点A,过点A作AB∥x轴交反比例函数(x<0)的图象于点B,C是x轴负半轴上一点,连接AC、BC,则△ABC的面积为( )
A.4 B.5 C.7 D.8
【解答】解:如图,连接OA、OB,线段AB交y轴于点D,
∵点A在反比例函数y图象上,点B在反比例函数y图象上,
∴S△AOD=1,S△BOD=3,
∴S△AOB=4,
∵AB∥x轴,
∴S△ABC=S△AOB=4.
故选:A.
二.填空题(共6小题)
9.(2025 湖南模拟)在平面直角坐标系中,若反比例函数y的图象经过点A(2m,1),B(﹣1,m﹣3),则k的值为 2 .
【解答】解:∵反比例函数y的图象经过点A(2m,1),B(﹣1,m﹣3),
∴2m×1=﹣1×(m﹣3),
解得:m=1,
∴A (2,1),
∴k=2.
故答案为:2.
10.(2025 温州模拟)如图,已知矩形ABCD的面积为16,AB⊥y轴,C,D是x轴上的两个点,点A,B分别在反比例函数的图象上,则a的值为 4 .
【解答】解:设点A坐标为(m,)(m>0,a>0),
∵AB⊥y轴,
∴点B坐标为(﹣3m,),
∴m |﹣3m| a+3a=16,
解得a=4,
故答案为:4.
11.(2025 福田区一模)如图,A(2,m),B(3,2)两点在反比例函数的图象上.若将横、纵坐标都是整数的点称为整点,则线段OA,OB及反比例函数图象上A,B两点之间的部分围成的区域(不含边界)中,整点的坐标为 (1,1)和(2,2) .
【解答】解:∵A(2,m),B(3,2)两点在反比例函数的图象上,
∴k=2m=3×2,
∴k=6,m=3,
∴反比例函数为y,A(2,3),
∵A(2,3),B(3,2),
∴直线OA为y1x,OB为y2x,
当x=1时,y1,y2,
当x=2时,y2,
∴线段OA,OB及反比例函数图象上A,B两点之间的部分围成的区域(不含边界)中整点有(1,1),(2,2).
故答案为:(1,1)和(2,2).
12.(2025 鹤壁一模)在平面直角坐标系xOy中,若函数的图象经过点(5,y1)和(﹣5,y2),则y1+y2的值是 0 .
【解答】解:∵函数的图象经过点(5,y1)和(﹣5,y2),
∴,,
∴,
故答案为:0.
13.(2025 立山区三模)如图,在平面直角坐标系中,已知射线OF平分由7个边长为1的小正方形组成图形的面积,且射线OF与反比例函数的交点A恰好在小正方形的边上,则k= .
【解答】解:如图,由图可知,点A的横坐标为﹣2,点H的纵坐标为3,
∵点A在反比例函数的图象上,
∴,A(﹣2,),
设直线OF的解析式为y=mx,由条件可得,
解得,
∴直线OF的解析式为,
把点H的纵坐标为3代入得到,
解得,
∴,
∴,
由条件可得,
解得,
经检验,是分式方程的解且符合题意.
故答案为:.
14.(2025 龙江县二模)如图,等边三角形ABC的顶点A,B分别在反比例函数图象的两个分支上,且点A,B关于原点对称,过点C作CD平行于x轴,交反比例函数的图象于点D,连接OC,OD,则△OCD的面积为 4 .
【解答】解:如图,过C、A作CM⊥x轴,AN⊥x轴于M、N,令CD交y轴于点H,则四边形CMOH是矩形,
∴∠CHO=∠DHO=90°,∠CMO=∠ONA=90°,S△COM=S△COH,
由对称可知OA=OB,OC⊥AB,
∴∠AOC=90°,
∵△ABC是等边三角形,
∴∠ACB=∠BAC=60°,
∴,
∵∠AOC=90°,AN⊥x轴,
∴∠OAN=90°﹣∠AON=∠COM,
∴△COM∽△OAN,
∴,
∴,
∴S△COH=S△COM=3S△OAN=3,
∴△OCD的面积为S△COM+S△ODH=3+1=4,
故答案为:4.
三.解答题(共7小题)
15.(2025 丹阳市二模)如图,直线y=﹣x+b与双曲线交于点A(1,3)和点B.
(1)求k、b的值;
(2)写出点B的坐标 (3,1) ;
(3)点M是x轴正半轴上一动点,当△ABM的面积为3时,直接写出点M的坐标 (1,0)或(7,0) .
【解答】解:(1)∵直线y=﹣x+b与双曲线交于点A(1,3),
∴3=﹣1+b,3,
∴k=3,b=4;
(2)解方程组,得或,
∴B(3,1).
故答案为:(3,1);
(3)令y=0,则y=﹣x+4=0,解得x=4,
∴C(4,0),
∵S△AMB=3,
∴S△AMB=S△AMC﹣S△BMC3,
∴MC=3,
∴M(1,0)或(7,0).
故答案为:(1,0)或(7,0).
16.(2025 河南模拟)如图,在平面直角坐标系中,已知一次函数y1=kx+b(k≠0)的图象与反比例函数的图象交于A,B两点,已知点A(1,4),点B的横坐标为﹣2.
(1)求一次函数与反比例函数的解析式;
(2)D为x轴上一点,若△ABD的面积为6,求点D的坐标;
(3)根据函数图象,直接写出不等式y1≤y2的解集.
【解答】解:(1)将A(1,4)代入y2得a=4,
∴反比例函数的解析式为y2,
将x=﹣2代入y2得y2=﹣2,
∴点B坐标为(﹣2,﹣2),
将A(1,4)B(﹣2,﹣2)代入y1=kx+b得
,解的,
∴y1=2x+2.
(2)设直线与x轴交点为C,将y=0代入y1=2x+2得x=﹣1
∴直线AB与x轴交点C的坐标为(﹣1,0),
设D点坐标为(n,0),
则S△ABD=S△ACD+S△BCDCD yACD |yB||﹣1﹣n|×4|﹣1﹣n|×2=3|﹣1﹣n|=6,
∴﹣1﹣n=2或﹣1﹣n=﹣2,解得n=﹣3或n=1,
∴点D坐标为(﹣3,0)或(1,0);
(3)由图象可得x≤﹣2或0<x≤1时,y1≤y2.
17.(2025 西市区校级模拟)国家规定,如果驾驶人员血液中每100毫升的酒精含量大于或等于20毫克且小于80毫克,则被认定为饮酒后驾车,如果每100毫升的血液中酒精含量大于或等于80毫克,则被认定为醉酒后驾车,且此时肝部正被严重损伤,一般成人饮用低度白酒0.25kg后,血液中酒精含量y(单位:毫克/百毫升)与时间x(单位:时)的关系可近似地用如图所示的图象表示.
(1)求OA所在直线及部分双曲线BC的函数表达式(不用写x的取值范围).
(2)饮用低度白酒0.25kg后,肝部被严重损伤会持续多少时间?
(3)假设某驾驶员晚上20:00在家喝完0.25kg低度白酒,第二天早上7:00能否驾车去上班?请判断并说明理由.
【解答】解:(1)设OA的函数表达式为y=kx,则:x=120,
∴k=100,
∴OA的函数表达式为y=100x,
可设部分双曲线BC的函数表达式为y,
由图象可知,当x=2时,y=120,
∴m=240,
∴部分双曲线BC的函数表达式为y;
(2)由(1)知y;
∴y80时,x=3;
当y=100x=80时,x=0.8,
∴饮用低度白酒0.25kg后,肝部被严重损伤会持续3﹣0.8=2.2小时.
(3)在y中,令y<20,
可得:20,
解之可得:x>12,
∵晚上20:00到第二天早上7:00的时间间隔为7+4=11(h),11h<12h,
∴某人晚上20:00喝完完0.25kg白酒,则此人第二天早上7:00时体内的酒精含量高于20(毫克/百毫升),
∴某人晚上20:00喝完完0.25kg低度白酒,则此人第二天早上7:00不能驾车出行.
18.(2025 涪城区三模)如图,一次函数y=kx+b(k≠0)的图象与反比例函数y(m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(1)求一次函数和反比例函数的解析式;
(2)若点E是点C关于x轴的对称点,求△ABE的面积.
【解答】解:(1)∵AD⊥x轴于点D,
∴AD∥y轴,
设A(a,2),
∴AD=2,
∵∠CAD=45°,
∴∠AFD=45°,
∴FD=AD=2,
连接AO,
∵AD∥y轴,
∴S△AOD=S△ADC=6,
∴OD=6,
∴A(6,2),
将A(6,2)代入,得m=12,
∴反比例函数解析式为y;
∵∠OCF=∠CAD=45°,
在△COF中,OC=OF=OD﹣FD=6﹣2=4,
∴C(0,﹣4),
将点A(6,2),点C(0,﹣4)代入y=kx+b,可得
,
∴,
∴一次函数解析式为y=x﹣4;
(2)点E是点C关于x轴的对称点,
∴E(0,4),
∴CE=8,
解方程组,
得 或,
∴B(﹣2,﹣6),
∴.
19.(2025 碧江区 模拟)在初二物理的学习中,我们知道压强p(Pa),压力F(N),受力面积S(m2)满足公式.
(1)当F为定值时,如图所示的图象能够正确反映p与S之间函数关系的图象是 ① (填序号);
(2)已知一块比较薄的冰面最多承受10000Pa的压强,小明的重量为600N.
①若小明的一双鞋底与冰面的接触面积共0.03m2,他能否安全地站在这块冰面上?
②若小明平躺在冰面上的一块质量不计的薄木板上,为了保证安全,这块薄木板的面积应满足什么条件?
【解答】解:(1)F为定值时,p与S之间是反比例函数的关系,且p随S的增大而减小,
∴p与S之间函数关系的图象是①.
故答案为:①.
(2)①当F=600,S=0.03时,p20000,
∵20000>10000,
∴他不能否安全地站在这块冰面上.
②根据题意,得10000,
解得S≥0.06.
答:这块薄木板的面积不能小于0.06m2.
20.(2025 越秀区校级二模)综合与实践:课题小空间检测视力问题
具体情境:对某班学生视力进行检测的任务:
现有条件:一张测试距离为5米的视力表,一间长为3.8米,宽为3.6米的空书房.
(1)如图1,若将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理可知:测试线应画在距离墙ABEF 1.2 米处;
(2)小明选择按比例制作视力表完成该任务,在制作过程中发现视力表上视力值V和该行字母E的宽度a之间的关系是一种函数模型,字母E的宽度a如图2所示,视力表上部分视力值V和字母E的宽度a的部分对应数据如所示:
位置 视力值V a的值(mm)
第1行 0.1 70
第5行 0.25 28
第8行 0.5 14
第14行 2 3.5
①根据表格数据判断,从一次函数、反比例函数中选择一个合适的函数模型拟合视力值V与字母E的宽度a(说明理由),并求出视力值V与字母E宽度a之间的函数关系式;
②小明在制作过程中发现某行字母E的宽度a的值17.5mm,请问该行对应的视力值是多少?
【解答】解:(1)5﹣3.8=1.2(米),
∴测试线应画在距离墙ABEF1.2米处,
故答案为:1.2.
(2)①∵视力值V与字母宽度a的乘积是定值7,
∴视力值V与字母宽度a成反比例函数关系.
设V,
把a=70,V=0.1,代入得到k=7,
∴视力值V与字母宽度a的函数关系是V.
②把a=17.5,代入V,得V=0.4,
∴该行对应的视力值是0.4.
21.(2025 青白江区模拟)如图1,已知点(a,b)为双曲线上一点,且,直线y=﹣x+t分别交x、y轴及双曲线于点A、B、C.
(1)求双曲线的解析式;
(2)如图2,连接OC.
①若t=8,在双曲线上找一点D,使得△OBD的面积是△OBC的面积的3倍,请求出此时点D的坐标;
②当t的值变化时,的值是否发生变化?若不变,求出它的值;若变化,请说明理由.
【解答】解:(1)∵,
∴,
∴.
∴a=﹣3,b=3.
∴k=﹣3×3=﹣9.
∴双曲线的解析式.
(2)①由题意,当t=8时,y=﹣x+8,令x=0,得y=8,
∴B(0,8),即OB=8.
令y=0,得﹣x+8=0,即x=8,
∴A(8,0),即OA=8,
又联立方程﹣x+8,
∴x=﹣1或x=9(x<0).
∴C(﹣1,9).
∴S△BOCOB |xC|8×1=4.
设点D的坐标为(m,﹣m),m<0,
∴.
∵S△DOB=3S△BOC=12
∴﹣4m=12.
∴m=﹣3.
∴D(﹣3,3).
②的值不发生变化,理由如下:过C作CH⊥y轴于H,
如图:在y=﹣x+t中,令x=0得y=t,令y=0得x=t,
∴OA=OB=t,
∴AB2=OA2+OB2=2OA2,.
∴△AOB是等腰直角三角形,∠ABO=45°=∠CBH.
∴△CBH是等腰直角三角形.
∴CH=BH.
设CH=BH=x,则OH=t+x,
∴OC2=OH2+CH2=(t+x)2+x2,
∴OC2﹣OA2=(t+x)2+x2﹣t2=2x(x+t),
由反比例函数可得,,
∴CH﹣OH=9,即x(x+t)=9,
∴OC2﹣OA2=2x(x+t)=18.
∴18,即的值不发生变化,为18.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
