2025秋高考物理复习第四章专题三天体运动突破专题课件
文档属性
| 名称 | 2025秋高考物理复习第四章专题三天体运动突破专题课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 816.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-05 17:38:17 | ||
图片预览








文档简介
(共29张PPT)
专题三
天体运动突破专题
突破 1 近地卫星、赤道上的物体及同步卫星的比较
1.同步卫星的六个“一定”.
2.近地卫星是在地球表面附近环绕地球做匀速圆周运动的卫
星,其运行的轨道半径可近似认为等于地球的半径,其运行线速
度约为 7.9 km/s,运行周期约为 85 min.
环绕体 近地卫星
(r1、ω1、v1、a1) 同步卫星
(r2、ω2、v2、a2) 赤道上随地球自转的物体(r3、ω3、v3、a3)
向心力 万有引力 万有引力 万有引力的一个分力
线速度 由 v=rω 得 v2>v3
v1>v2>v3
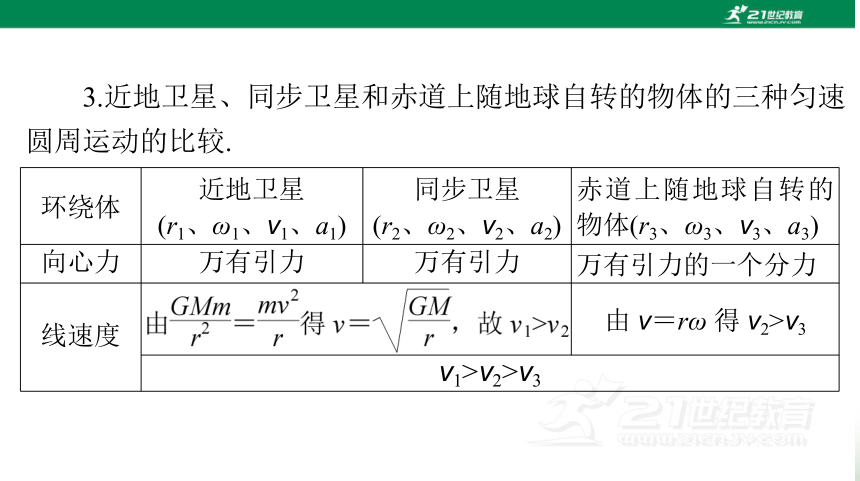
3.近地卫星、同步卫星和赤道上随地球自转的物体的三种匀速
圆周运动的比较.
环绕体 近地卫星
(r1、ω1、v1、a1) 同步卫星
(r2、ω2、v2、a2) 赤道上随地球自转的物体(r3、ω3、v3、a3)
向心加
速度 由 a=ω2r 得 a2>a3
a1>a2>a3
轨道半径 r2>r3=r1
(续表)
环绕体 近地卫星
(r1、ω1、v1、a1) 同步卫星
(r2、ω2、v2、a2) 赤道上随地球自转的物体(r3、ω3、v3、a3)
角速度
ω1>ω2 同步卫星的角速度与地球自转角速度相同,故 ω2=ω3
ω1>ω2=ω3
(续表)
【典题1】(多选,2024 年天津卷)卫星未发射时静置在赤道上
随地球转动,地球半径为 R.卫星发射后在地球同步轨道上做匀速
)
圆周运动,轨道半径为 r.则卫星未发射时和在轨道上运行时(
A.角速度之比为 1∶1
B.线速度之比为
C.向心加速度之比为 R∶r
D.受到地球的万有引力之比为 R2∶r2
解析:卫星未发射时静置在赤道上随地球转动,角速度与地
球自转角速度相等,卫星发射后在地球同步轨道上做匀速圆周运
动,角速度与地球自转角速度相等,则卫星未发射时和在轨道上
运行时角速度之比为 1∶1,A 正确;由公式 v=ωr 可知,卫星未
发射时和在轨道上运行时,由于角速度相等,则线速度之比为轨
道半径之比 R∶r,B 错误;由公式an=ω2r 可知,卫星未发射时
和在轨道上运行时,由于角速度相等,则向心加速度之比为轨道
r
半径之比 R∶r,C 正确;由公式 F=
GMm
2
可知,卫星未发射时和
在轨道上运行时,受到地球的万有引力之比与轨道半径的平方成
反比,即 r2∶R2,D 错误.
答案:AC
突破 2 卫星的变轨问题
1.卫星轨道的渐变:当卫星由于某种原因,速度逐渐改变时,
万有引力不再等于向心力,卫星将变轨运行.
2.卫星轨道的突变:由于技术上的需要,有时要在适当的位
置短时间内启动飞行器上的发动机,使飞行器轨道发生突变,使
其进入预定的轨道.如图所示,发射同步卫星时,可以分多过程
完成:
(1)先将卫星送到近地轨道Ⅰ.
(2)使其绕地球做匀速圆周运动,速率为 v1,变轨时在 P 点点
火加速,短时间内将速率由 v1 增加到 v2,使卫星进入椭圆形的转
移轨道Ⅱ.
(3)卫星运行到远地点 Q 时的速率为 v3,此时进行第二次点火
加速,在短时间内将速率由 v3 增加到 v4,使卫星进入同步轨道Ⅲ,
绕地球做匀速圆周运动.
【典题2】(2024 年安徽卷)2024 年 3 月 20 日,我国探月工程
四期鹊桥二号中继星成功发射升空.当抵达距离月球表面某高度
时,鹊桥二号开始进行近月制动,并顺利进入捕获轨道运行,如
图所示,轨道的半长轴约为 51 900 km.后经多次轨道调整,进入冻
结轨道运行,轨道的半长轴约为 9900 km,周期约为 24 h.则鹊桥
二号在捕获轨道运行时(
)
A.周期约为 144 h
B.近月点的速度大于远月点的速度
C.近月点的速度小于在冻结轨道运行时近月点的速度
D.近月点的加速度大于在冻结轨道运行时近月点的加速度
解析:冻结轨道和捕获轨道的中心天体是月球,根据开普勒
普勒第二定律得,近月点的速度大于远月点的速度,B 正确;近
月点从捕获轨道到冻结轨道鹊桥二号进行近月制动,捕获轨道近
月点的速度大于在冻结轨道运行时近月点的速度,C 错误;两轨
道的近月点所受的万有引力相同,根据牛顿第二定律可知,近月
点的加速度等于在冻结轨道运行时近月点的加速度,D 错误.
答案:B
突破 3 天体的追及问题
“天体相遇”,指两天体相距最近.若两环绕天体的运转轨道
在同一平面内,则两环绕天体与中心天体在同一
直线上,且位于中心天体的同侧(或异侧)时相距
最近(或最远),类似于在田径场赛道上的循环长
跑比赛,跑得快的每隔一段时间多跑一圈追上并
超过跑得慢的,如图所示.解决这类问题有两种常
用方法:
1.角度关系.
设天体1(离中心近些)与天体2某时刻相距最近,如果经过时间t,两天体与中心连线半径转过的角度之差(或和)等于2π的整数倍,则两天体又相距最近,即ω1t-ω2t=2nπ(n=1,2,3,…)(同向)或 ω1t+ω2t=2nπ(n=1,2,3,…)(反向);如果经过时间 t′,两天体与中心连线半径转过的角度之差(或和)等于π的奇数倍,则两天体又相距最远,即ω1t′-ω2t′=(2n-1)π(n=1,2,3,…)(同向)或 ω1t′+ω2t′=(2n-1)π(n=1,2,3,…)(反向).
2.圈数关系.
【典题 3】如图所示,有 A、B 两颗行星绕同一颗质量为
M 的恒星做圆周运动,旋转方向相同,A 行星的周期为 T1,B
行星的周期为 T2,在某一时刻两行星相距最近,则:
(1)经过多长时间,两行星再次相距最近?
(2)经过多长时间,两行星第一次相距最远?
解:A、B 两颗行星做匀速圆周运动,由万有引力提供向心力,
一周时,B 还没有运动完一周,但是要它们相距最近,只有 A、B
两行星和恒星的连线再次在一条直线上,且 A、B 在恒星的同侧,
从角度上看,在相同时间内,A 比 B 多转了 2π.如果 A、B 在恒星
的两侧,则它们相距最远,从角度上看,在相同时间内,A 比 B
多转了π.
方法技巧
处理天体相距最近和最远的问题,实际上就是因
为越向外的卫星运行得越慢,当里边的比外边的卫星多走了半圈
或半圈的奇数倍时相距最远,多走了整数圈时相距最近.
突破 4 非常规“卫星”问题
通常的卫星是指仅仅在中心天体万有引力作用下做无动力飞
行的卫星,各参量与轨道半径的关系也是针对这种卫星的,不满
足以上条件的卫星,同样也不适应常见卫星的运行规律.如飞机,
有动力,线速度与高度无关;连续物,整个连续物上各点角速度
大小相等,其角速度、线速度等规律与卫星的相反;某个飞行物
同时受到两个物体的引力,如同时受到地球和月球的引力,也不
满足常见卫星的运行规律.
【典题 4】(2023 年四川成都三模)如图甲所示,电影《流浪
地球 2》中的“太空电梯”令人震撼.“太空电梯”的结构设计如
图乙所示,地球半径约 6400 km,“太空电梯”空间站位于离地
面约 36 000 km 的地球同步轨道上,其上方约 54 000 km 高度有平
衡锤,空间站上、下方均用缆绳分别连接地面和平衡锤,运载仓
与缆绳间的作用力可忽略.下列说法正确的是(
)
甲
乙
A.运载仓由地面上升至空间站的过程中始终处于失重状态
B.连接空间站的上、下两根缆绳对空间站的拉力大小相等
C.平衡锤、空间站的加速度 a锤、a站与地球表面重力加速度 g
的大小关系为 a锤>g>a站
D.若平衡锤下方的缆绳突然断裂,则平衡锤将做近心运动跌
落至地球表面
解析:根据“太空电梯”结构可知 v=ωr,运载仓由地面上
升至空间站的过程中,角速度不变,线速度逐渐增大,运载仓不
是始终处于失重状态,A 错误;由于“太空电梯”空间站处于地球
同步轨道上,可知地球对它的万有引力刚好提供其绕地球做匀速
圆周运动所需的向心力,则连接空间站的上、下两根缆绳对空间
站的拉力大小相等,方向相反,B 正确;对于“太空电梯”空间站,
锤、空间站的加速度 a锤、a站与地球表面重力加速度 g 的大小关系
为 g>a锤>a站,C 错误;根据题意可知,若平衡锤下方的缆绳突然断
裂,平衡锤与地球之间的万有引力将不足以提供平衡锤做圆周运
动所需的向心力,因此平衡锤将做离心运动,D 错误.
答案:B
专题三
天体运动突破专题
突破 1 近地卫星、赤道上的物体及同步卫星的比较
1.同步卫星的六个“一定”.
2.近地卫星是在地球表面附近环绕地球做匀速圆周运动的卫
星,其运行的轨道半径可近似认为等于地球的半径,其运行线速
度约为 7.9 km/s,运行周期约为 85 min.
环绕体 近地卫星
(r1、ω1、v1、a1) 同步卫星
(r2、ω2、v2、a2) 赤道上随地球自转的物体(r3、ω3、v3、a3)
向心力 万有引力 万有引力 万有引力的一个分力
线速度 由 v=rω 得 v2>v3
v1>v2>v3
3.近地卫星、同步卫星和赤道上随地球自转的物体的三种匀速
圆周运动的比较.
环绕体 近地卫星
(r1、ω1、v1、a1) 同步卫星
(r2、ω2、v2、a2) 赤道上随地球自转的物体(r3、ω3、v3、a3)
向心加
速度 由 a=ω2r 得 a2>a3
a1>a2>a3
轨道半径 r2>r3=r1
(续表)
环绕体 近地卫星
(r1、ω1、v1、a1) 同步卫星
(r2、ω2、v2、a2) 赤道上随地球自转的物体(r3、ω3、v3、a3)
角速度
ω1>ω2 同步卫星的角速度与地球自转角速度相同,故 ω2=ω3
ω1>ω2=ω3
(续表)
【典题1】(多选,2024 年天津卷)卫星未发射时静置在赤道上
随地球转动,地球半径为 R.卫星发射后在地球同步轨道上做匀速
)
圆周运动,轨道半径为 r.则卫星未发射时和在轨道上运行时(
A.角速度之比为 1∶1
B.线速度之比为
C.向心加速度之比为 R∶r
D.受到地球的万有引力之比为 R2∶r2
解析:卫星未发射时静置在赤道上随地球转动,角速度与地
球自转角速度相等,卫星发射后在地球同步轨道上做匀速圆周运
动,角速度与地球自转角速度相等,则卫星未发射时和在轨道上
运行时角速度之比为 1∶1,A 正确;由公式 v=ωr 可知,卫星未
发射时和在轨道上运行时,由于角速度相等,则线速度之比为轨
道半径之比 R∶r,B 错误;由公式an=ω2r 可知,卫星未发射时
和在轨道上运行时,由于角速度相等,则向心加速度之比为轨道
r
半径之比 R∶r,C 正确;由公式 F=
GMm
2
可知,卫星未发射时和
在轨道上运行时,受到地球的万有引力之比与轨道半径的平方成
反比,即 r2∶R2,D 错误.
答案:AC
突破 2 卫星的变轨问题
1.卫星轨道的渐变:当卫星由于某种原因,速度逐渐改变时,
万有引力不再等于向心力,卫星将变轨运行.
2.卫星轨道的突变:由于技术上的需要,有时要在适当的位
置短时间内启动飞行器上的发动机,使飞行器轨道发生突变,使
其进入预定的轨道.如图所示,发射同步卫星时,可以分多过程
完成:
(1)先将卫星送到近地轨道Ⅰ.
(2)使其绕地球做匀速圆周运动,速率为 v1,变轨时在 P 点点
火加速,短时间内将速率由 v1 增加到 v2,使卫星进入椭圆形的转
移轨道Ⅱ.
(3)卫星运行到远地点 Q 时的速率为 v3,此时进行第二次点火
加速,在短时间内将速率由 v3 增加到 v4,使卫星进入同步轨道Ⅲ,
绕地球做匀速圆周运动.
【典题2】(2024 年安徽卷)2024 年 3 月 20 日,我国探月工程
四期鹊桥二号中继星成功发射升空.当抵达距离月球表面某高度
时,鹊桥二号开始进行近月制动,并顺利进入捕获轨道运行,如
图所示,轨道的半长轴约为 51 900 km.后经多次轨道调整,进入冻
结轨道运行,轨道的半长轴约为 9900 km,周期约为 24 h.则鹊桥
二号在捕获轨道运行时(
)
A.周期约为 144 h
B.近月点的速度大于远月点的速度
C.近月点的速度小于在冻结轨道运行时近月点的速度
D.近月点的加速度大于在冻结轨道运行时近月点的加速度
解析:冻结轨道和捕获轨道的中心天体是月球,根据开普勒
普勒第二定律得,近月点的速度大于远月点的速度,B 正确;近
月点从捕获轨道到冻结轨道鹊桥二号进行近月制动,捕获轨道近
月点的速度大于在冻结轨道运行时近月点的速度,C 错误;两轨
道的近月点所受的万有引力相同,根据牛顿第二定律可知,近月
点的加速度等于在冻结轨道运行时近月点的加速度,D 错误.
答案:B
突破 3 天体的追及问题
“天体相遇”,指两天体相距最近.若两环绕天体的运转轨道
在同一平面内,则两环绕天体与中心天体在同一
直线上,且位于中心天体的同侧(或异侧)时相距
最近(或最远),类似于在田径场赛道上的循环长
跑比赛,跑得快的每隔一段时间多跑一圈追上并
超过跑得慢的,如图所示.解决这类问题有两种常
用方法:
1.角度关系.
设天体1(离中心近些)与天体2某时刻相距最近,如果经过时间t,两天体与中心连线半径转过的角度之差(或和)等于2π的整数倍,则两天体又相距最近,即ω1t-ω2t=2nπ(n=1,2,3,…)(同向)或 ω1t+ω2t=2nπ(n=1,2,3,…)(反向);如果经过时间 t′,两天体与中心连线半径转过的角度之差(或和)等于π的奇数倍,则两天体又相距最远,即ω1t′-ω2t′=(2n-1)π(n=1,2,3,…)(同向)或 ω1t′+ω2t′=(2n-1)π(n=1,2,3,…)(反向).
2.圈数关系.
【典题 3】如图所示,有 A、B 两颗行星绕同一颗质量为
M 的恒星做圆周运动,旋转方向相同,A 行星的周期为 T1,B
行星的周期为 T2,在某一时刻两行星相距最近,则:
(1)经过多长时间,两行星再次相距最近?
(2)经过多长时间,两行星第一次相距最远?
解:A、B 两颗行星做匀速圆周运动,由万有引力提供向心力,
一周时,B 还没有运动完一周,但是要它们相距最近,只有 A、B
两行星和恒星的连线再次在一条直线上,且 A、B 在恒星的同侧,
从角度上看,在相同时间内,A 比 B 多转了 2π.如果 A、B 在恒星
的两侧,则它们相距最远,从角度上看,在相同时间内,A 比 B
多转了π.
方法技巧
处理天体相距最近和最远的问题,实际上就是因
为越向外的卫星运行得越慢,当里边的比外边的卫星多走了半圈
或半圈的奇数倍时相距最远,多走了整数圈时相距最近.
突破 4 非常规“卫星”问题
通常的卫星是指仅仅在中心天体万有引力作用下做无动力飞
行的卫星,各参量与轨道半径的关系也是针对这种卫星的,不满
足以上条件的卫星,同样也不适应常见卫星的运行规律.如飞机,
有动力,线速度与高度无关;连续物,整个连续物上各点角速度
大小相等,其角速度、线速度等规律与卫星的相反;某个飞行物
同时受到两个物体的引力,如同时受到地球和月球的引力,也不
满足常见卫星的运行规律.
【典题 4】(2023 年四川成都三模)如图甲所示,电影《流浪
地球 2》中的“太空电梯”令人震撼.“太空电梯”的结构设计如
图乙所示,地球半径约 6400 km,“太空电梯”空间站位于离地
面约 36 000 km 的地球同步轨道上,其上方约 54 000 km 高度有平
衡锤,空间站上、下方均用缆绳分别连接地面和平衡锤,运载仓
与缆绳间的作用力可忽略.下列说法正确的是(
)
甲
乙
A.运载仓由地面上升至空间站的过程中始终处于失重状态
B.连接空间站的上、下两根缆绳对空间站的拉力大小相等
C.平衡锤、空间站的加速度 a锤、a站与地球表面重力加速度 g
的大小关系为 a锤>g>a站
D.若平衡锤下方的缆绳突然断裂,则平衡锤将做近心运动跌
落至地球表面
解析:根据“太空电梯”结构可知 v=ωr,运载仓由地面上
升至空间站的过程中,角速度不变,线速度逐渐增大,运载仓不
是始终处于失重状态,A 错误;由于“太空电梯”空间站处于地球
同步轨道上,可知地球对它的万有引力刚好提供其绕地球做匀速
圆周运动所需的向心力,则连接空间站的上、下两根缆绳对空间
站的拉力大小相等,方向相反,B 正确;对于“太空电梯”空间站,
锤、空间站的加速度 a锤、a站与地球表面重力加速度 g 的大小关系
为 g>a锤>a站,C 错误;根据题意可知,若平衡锤下方的缆绳突然断
裂,平衡锤与地球之间的万有引力将不足以提供平衡锤做圆周运
动所需的向心力,因此平衡锤将做离心运动,D 错误.
答案:B
同课章节目录
