2025秋高考物理复习第五章第1节功和功率课件
文档属性
| 名称 | 2025秋高考物理复习第五章第1节功和功率课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-05 17:38:17 | ||
图片预览











文档简介
(共47张PPT)
第五章
机械能
课标要求 热点考向
1.举例说明功是能量变化的量度,理解功和功率.关心生活和生产
中常见机械功率的大小及其意义
2.通过实验,探究恒力做功与物体动能变化的关系.理解动能和动
能定理.用动能定律解释生活和生产中的现象
3.理解重力势能.知道重力势能的变化和重力做功的关系
4.通过实验,验证机械能守恒定律.理解机械能守恒定律.用机械能
守恒定律分析生活和生产中的有关问题
5.了解自然界中存在多种形式的能量.知道能量守恒是最基本、最
普遍的自然规律之一
6.通过能量守恒以及能量转化和转移的方向性,认识提高效率的
重要性.了解能源与人类生存和社会发展的关系,知道可持续发展
的重大意义 1.功和功率问题
2.动能定理的应用
3.机械能守恒的条件
4.机械能守恒定律与平抛
运动、圆周运动的综合
5.功能关系与能量守恒
第1节
功和功率
一、功
力的方向
力的方向
量度
1.定义:一个物体受到力的作用,如果在________上发生了一
段位移,就说这个力对物体做了功.
2.必要因素:力和物体在_________上发生的位移.
3.物理意义:功是能量转化的________.
4.计算公式.
Fl
Flcos α
(1)恒力 F 的方向与位移 l 的方向一致时:W=________.
(2)恒力 F 的方向与位移l的方向成某一夹角 α 时:W=
________.
5.功的正负.
正功
负功
不做功
二、功率
快慢
时间
1.功率:描述做功________的物理量.
2.定义:功跟完成功所用________的比值叫做功率.
3.功率的计算.
W
t
Fv·cos α
(1)P=______,只能计算 t 时间内的平均功率.
(2)P=________.若 v 为平均速度,则 P 为平均功率;若 v 为
瞬时速度,则 P 为瞬时功率;α 表示 F 与 v 的夹角.
【基础自测】
1.判断下列题目的正误.
(1)一个力对物体做了负功,则说明这个力一定阻碍物体的运
动.(
)
(2)作用力做正功时,反作用力一定做负功.(
)
(3)力对物体做功的正负是由力和位移间的夹角大小决定的.
(
)
(4)汽车上坡时换成低挡位,其目的是减小速度得到较大的牵
引力.(
)
(5)合力的功等于各力功的矢量和.(
答案:(1)√ (2)× (3)√ (4)√ (5)×
)
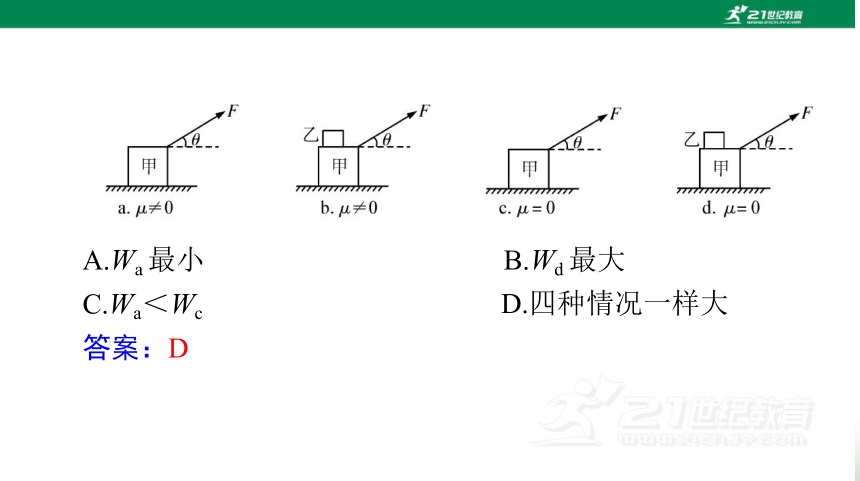
2.如图所示的 a、b、c、d 中,质量为 M 的物体甲受到相同
的恒力 F 的作用,在力 F 作用下物体甲在水平方向移动相同的位
移.μ表示物体甲与水平面间的动摩擦因数,乙是随物体甲一起运
动的小物块,比较物体甲移动的过程中力 F 对甲所做的功的大
小,下列选项正确的是(
)
B.Wd 最大
D.四种情况一样大
A.Wa 最小
C.Wa<Wc
答案:D
3.物体在两个相互垂直的力 F1、F2 作用下运动,力 F1 对物体
做功 6 J,力 F2 对物体做功 8 J,则 F1 、F2 的合力对物体做功为
(
)
B.10 J
D.-2 J
A.14 J
C.2 J
答案:A
4.(2024 年浙江卷) 一个音乐喷泉喷头出水口的横截面积为
2×10-4 m2,喷水速度约为10 m/s,水的密度为1×103 kg/m3,则该
)
喷头喷水的功率约为(
A.10 W
C.100 W
B.20 W
D.200 W
答案:C
判断依据 适用情况
根据力和位移方向的夹角判断 常用于恒力做功的判断
根据力和瞬时速度方向的夹角判断 常用于质点做曲线运动
根据功能关系或能量守恒定律判断 常用于变力做功的判断
热点 1 功的理解与计算
[热点归纳]
1.判断力是否做功及做正、负功的方法.
定义法 用力乘以力方向上的位移,比如重力做功就是用重力乘
以重力方向上的位移,根据力和力的方向上位移的方向
关系判断功的正负
计算
式法 根据功的计算式 W=Fscos α,需要注意的是位移 s 为
对地位移(严格讲是力的作用点的位移),α为力的方向
与位移方向的夹角
2.恒力做功的计算方法.
考向 1 正负功的判断
【典题 1】如图所示,光滑的水平面上放着一辆小车,站
在小车上的人拉系在墙壁上的水平绳子,使小车和人一起向右
)
加速移动.则下列说法正确的是(
A.绳子的拉力对人做了负功
B.绳子的拉力对小车做了正功
C.小车对人的摩擦力对人做了正功
D.人对小车的摩擦力对小车做了正功
解析:人受到绳子的拉力与人的位移方向相同,所以绳子的
拉力对人做正功.由于拉力未作用在小车上,所以拉力对小车不做
功, AB 错误;小车对人的摩擦力方向向左,则小车对人的摩擦
力对人做负功, C 错误;人对小车的静摩擦力方向向右,则静
摩擦力对小车做正功, D 正确.
答案:D
考向 2 功的计算
【典题 2】(2023 年北京卷)如图所示,一物体在力 F 作用
下沿水平桌面做匀加速直线运动.已知物体质量为 m,加速度大
小为 a,物体和桌面之间的动摩擦因数为 μ,重力加速度为 g,在
)
物体移动距离为 x 的过程中,下列说法正确的是(
A.摩擦力做功大小与力 F 的方向无关
B.合力做功大小与力 F 的方向有关
C.力 F 为水平方向时,F 做功为μmgx
D.力 F 做功的最小值为 max
解析:因合力做功为 max 且大小一定,而合力做的功等于力
F 与摩擦力 f 做功的代数和,而当 F sin θ=mg 时,摩擦力 f=0,
则此时摩擦力做功为零,此时力 F 做功最小,最小值为 max,D
正确.
答案:D
热点 2 功率的分析和计算
[热点归纳]
瞬时功率
的计算 P=Fvcos α,其中v为物体运动的瞬时速度,α为力的方向与瞬时速度方向的夹角
P=F·vF,其中vF为物体的速度v在力F方向上的分速度;P=Fv·v,其中Fv为物体受到的外力F在速度v方向上的分力
(续表)
考向 1 平均功率
【典题 3】(2023 年山东卷)《天工开物》中记载了古人借助
水力使用高转筒车往稻田里引水的场景(如图所示).引水过程简化
如下:两个半径均为 R 的水轮,以角速度ω匀速转动.水筒在筒车
上均匀排布,单位长度上有 n 个,与水轮间无相对滑动.每个水
筒离开水面时装有质量为 m 的水,其中的 60%被输送到高出水面
H 处灌入稻田.当地的重力加速度为 g,则筒车对灌入稻田的水做
功的功率为(
)
A.
2nmgω2RH
5
B.
3nmgωRH
5
3nmgω2RH
C.
5
D.nmgωRH
解析:每个水筒中水的重力为 G=mg,水筒的线速度为 v=
ωR,t 时间内,装水的水筒个数为 N=nvt=nωRt,筒车对灌入稻
答案:B
思路引导
本题为非质点模型,选取一个周期的时间,所有
的水筒及水均从最低点上升到最高点.
考向 2 瞬时功率
【典题4】(2024 年贵州卷)质量为 1 kg 的物块静置于光滑水
平地面上,设物块静止时的位置为 x 轴零点.现给物块施加一沿 x
轴正方向的水平力 F,其大小随位置x变化的关系如图所示,则物
块运动到 x=3 m 处,F 做功的瞬时功率为(
)
A.8 W
B.16 W
C.24 W
D.36 W
解析:根据图像可知物块运动到 x=3 m 处,F 做的总功为
得物块运动到 x=3 m 处时的速度为 v=4 m/s,故此时 F 做功的瞬
时功率为 P=Fv=8 W,A 正确.
答案:A
两种方式 以恒定功率启动 以恒定加速度启动
P t 图和
v t 图
热点 3 机车的启动运行
[热点归纳]
1.两种启动方式的比较.
(续表)
(续表)
=
率最大,但速度不是最大,v=2.三个重要关系式.
(1)无论哪种启动过程,机车的最大速度都等于其匀速运动时的
速度,即vm=
P P
Fmin F阻
(式中 Fmin 为最小牵引力,其值等于阻力 F阻).
(2)机车以恒定加速度启动的过程中,匀加速过程结束时,功
P P
F F阻
.
(3)机车以恒定功率启动时,牵引力做的功 W=Pt.由动能定理
得:Pt-F阻 x=ΔEk.此式经常用于求解机车以恒定功率启动过程的
位移大小.
【典题 5】(2023 年湖北卷)两节动车的额定功率分别为 P1 和
P2,在某平直铁轨上能达到的最大速度分别为 v1 和 v2.现将他们编
成动车组,设每节动车运行时受到的阻力在编组前后不变,则该
动车组在此铁轨上能达到的最大速度为(
)
答案:D
思路导引
动车组在此铁轨上达到最大速度时,动车组所受
合力为 0,阻力为两部分的阻力之和,牵引力为两部分的牵引力之
和.
变力做功的计算方法
求力做功时,一定要注意分析是求恒力做的功还是变力做的
功,如果是求变力做的功,还有以下 4 种方法.
方法 常见情境 方法概述
微元法 将物体的位移分割成许多小段,因小段很小,每一小段上作用在物体上的力可以视为恒力,这样就将变力做功转化为在无数个无穷小的位移方向上的恒力所做功的代数和.此法在中学阶段,常应用于求解大小不变、方向改变的变力做功问题
方法 常见情境 方法概述
平均
力法 在求解变力做功时,若物体受到的力方
向不变,而大小随位移呈线性变化,即
力均匀变化时,则可以认为物体受到一
F1+F2
大小为 F = 的恒力作用,F1 、F2
2
分别为物体初、末态所受到的力,然后
用公式 W=F lcos α求此力所做的功
(续表)
方法 常见情境 方法概述
图像法 在 F-x 图像中,图线与 x 轴所围“面积”
的代数和就表示力 F 在这段位移所做的
功,且位于 x 轴上方的“面积”为正,位
于 x 轴下方的“面积”为负,但此方法只
便于求图线所围图形规则的情况(如三角
形、矩形、圆等规则的几何图形)
(续表)
方法 常见情境 方法概述
等效转
换法 变力做功直接求解时,通常都比较复杂,
但若通过转换研究对象,有时可化为恒
力做功,用 W=Flcos ɑ求解. 此法常常应
用于轻绳通过定滑轮拉物体的问题中
恒力 F 把物块从 A 拉到 B,绳子对物块
(续表)
模型一 微元法
【典题 6】(2021 年山东济南质检)如图所示,一质量为m=
0.1 kg 的小方块(可视为质点)系在一伸直的轻绳一端,绳的另一
端固定在摩擦因数μ=0.2 的粗糙水平面上,绳长 r=1 m.给小方
以绳长为半径做圆周运动,重力加速度为 g 取 10 m/s2,当小方块
恰好运动一周时,绳子拉力为(
)
B.0.8π N
D.0.2π N
A.π N
C.0.4π N
答案:D
模型二 平均力法
【典题 7】当前,我国某些贫困地区的日常用水仍然依靠井水.
某同学用水桶从水井里提水,井内水面到井口的高度为 20 m.水桶
离开水面时,桶和水的总质量为 10 kg.由于水桶漏水,在被匀速提
升至井口的过程中,桶和水的总质量随着上升距离的变化而变化,
其关系如图所示.水桶可以看成质点,不计空气阻力,重力加速
度 g 取 10 m/s2.由图像可知,在提水的整个过程中,拉力对水
桶做的功为(
)
A.2000 J
B.1800 J
C.200 J
D.180 J
F1+F2
解析:由于水桶匀速上升,故拉力等于水桶重力.由于水和水
桶的质量随位移均匀减小.故拉力与位移满足线性关系,所以可用
平均力法求解变力做功.F1=m1g=100 N,F2=m2g=80 N,则拉力
2
x=1800 J.
做功为:W拉=
答案:B
模型三 图像法
【典题 8】一物体所受的力 F 随位移 x 变化的图像如图
)
所示,求在这一过程中,力 F 对物体做的功为(
A.3 J
B.6 J
C.7 J
D.8 J
解析:力 F 对物体做的功等于 x 轴上方梯形“面积”所表示
的正功与 x 轴下方三角形“面积”所表示的负功的代数之和.W1=
物体做的功为 W=7 J-1 J=6 J.B 正确.
答案:B
思路导引
力 F 随位移 x 变化的图像中,图像与坐标轴所围
成图形的面积等于力做的功,结合图像特点知,前 5 m 内力做的
功与前 3 m 内力做的功相同.
模型四 等效转换法
【典题 9】人在 A 点拉着绳通过一定滑轮吊起质量 m=50 kg
的物体,如图所示,开始时绳与水平方向的夹角为 60°.当人匀
速提起物体由 A 点沿水平方向运动 L=2 m 而到达 B 点时,绳与
水平方向成 30°角.则人对绳的拉力做了多少功?(g 取 10 m/s2)
解:人对绳的拉力做功与绳对物体的拉力做功是相同的,而
由于匀速提升物体,故物体处于平衡状态,可知绳上拉力 F=mg.
而物体上升的高度 h 等于右侧绳子的变化量ΔL,由几何关系得
解得ΔL≈1.46 m
所以,人对绳子做的功
W=mgΔL=500×1.46 J=730 J.
第五章
机械能
课标要求 热点考向
1.举例说明功是能量变化的量度,理解功和功率.关心生活和生产
中常见机械功率的大小及其意义
2.通过实验,探究恒力做功与物体动能变化的关系.理解动能和动
能定理.用动能定律解释生活和生产中的现象
3.理解重力势能.知道重力势能的变化和重力做功的关系
4.通过实验,验证机械能守恒定律.理解机械能守恒定律.用机械能
守恒定律分析生活和生产中的有关问题
5.了解自然界中存在多种形式的能量.知道能量守恒是最基本、最
普遍的自然规律之一
6.通过能量守恒以及能量转化和转移的方向性,认识提高效率的
重要性.了解能源与人类生存和社会发展的关系,知道可持续发展
的重大意义 1.功和功率问题
2.动能定理的应用
3.机械能守恒的条件
4.机械能守恒定律与平抛
运动、圆周运动的综合
5.功能关系与能量守恒
第1节
功和功率
一、功
力的方向
力的方向
量度
1.定义:一个物体受到力的作用,如果在________上发生了一
段位移,就说这个力对物体做了功.
2.必要因素:力和物体在_________上发生的位移.
3.物理意义:功是能量转化的________.
4.计算公式.
Fl
Flcos α
(1)恒力 F 的方向与位移 l 的方向一致时:W=________.
(2)恒力 F 的方向与位移l的方向成某一夹角 α 时:W=
________.
5.功的正负.
正功
负功
不做功
二、功率
快慢
时间
1.功率:描述做功________的物理量.
2.定义:功跟完成功所用________的比值叫做功率.
3.功率的计算.
W
t
Fv·cos α
(1)P=______,只能计算 t 时间内的平均功率.
(2)P=________.若 v 为平均速度,则 P 为平均功率;若 v 为
瞬时速度,则 P 为瞬时功率;α 表示 F 与 v 的夹角.
【基础自测】
1.判断下列题目的正误.
(1)一个力对物体做了负功,则说明这个力一定阻碍物体的运
动.(
)
(2)作用力做正功时,反作用力一定做负功.(
)
(3)力对物体做功的正负是由力和位移间的夹角大小决定的.
(
)
(4)汽车上坡时换成低挡位,其目的是减小速度得到较大的牵
引力.(
)
(5)合力的功等于各力功的矢量和.(
答案:(1)√ (2)× (3)√ (4)√ (5)×
)
2.如图所示的 a、b、c、d 中,质量为 M 的物体甲受到相同
的恒力 F 的作用,在力 F 作用下物体甲在水平方向移动相同的位
移.μ表示物体甲与水平面间的动摩擦因数,乙是随物体甲一起运
动的小物块,比较物体甲移动的过程中力 F 对甲所做的功的大
小,下列选项正确的是(
)
B.Wd 最大
D.四种情况一样大
A.Wa 最小
C.Wa<Wc
答案:D
3.物体在两个相互垂直的力 F1、F2 作用下运动,力 F1 对物体
做功 6 J,力 F2 对物体做功 8 J,则 F1 、F2 的合力对物体做功为
(
)
B.10 J
D.-2 J
A.14 J
C.2 J
答案:A
4.(2024 年浙江卷) 一个音乐喷泉喷头出水口的横截面积为
2×10-4 m2,喷水速度约为10 m/s,水的密度为1×103 kg/m3,则该
)
喷头喷水的功率约为(
A.10 W
C.100 W
B.20 W
D.200 W
答案:C
判断依据 适用情况
根据力和位移方向的夹角判断 常用于恒力做功的判断
根据力和瞬时速度方向的夹角判断 常用于质点做曲线运动
根据功能关系或能量守恒定律判断 常用于变力做功的判断
热点 1 功的理解与计算
[热点归纳]
1.判断力是否做功及做正、负功的方法.
定义法 用力乘以力方向上的位移,比如重力做功就是用重力乘
以重力方向上的位移,根据力和力的方向上位移的方向
关系判断功的正负
计算
式法 根据功的计算式 W=Fscos α,需要注意的是位移 s 为
对地位移(严格讲是力的作用点的位移),α为力的方向
与位移方向的夹角
2.恒力做功的计算方法.
考向 1 正负功的判断
【典题 1】如图所示,光滑的水平面上放着一辆小车,站
在小车上的人拉系在墙壁上的水平绳子,使小车和人一起向右
)
加速移动.则下列说法正确的是(
A.绳子的拉力对人做了负功
B.绳子的拉力对小车做了正功
C.小车对人的摩擦力对人做了正功
D.人对小车的摩擦力对小车做了正功
解析:人受到绳子的拉力与人的位移方向相同,所以绳子的
拉力对人做正功.由于拉力未作用在小车上,所以拉力对小车不做
功, AB 错误;小车对人的摩擦力方向向左,则小车对人的摩擦
力对人做负功, C 错误;人对小车的静摩擦力方向向右,则静
摩擦力对小车做正功, D 正确.
答案:D
考向 2 功的计算
【典题 2】(2023 年北京卷)如图所示,一物体在力 F 作用
下沿水平桌面做匀加速直线运动.已知物体质量为 m,加速度大
小为 a,物体和桌面之间的动摩擦因数为 μ,重力加速度为 g,在
)
物体移动距离为 x 的过程中,下列说法正确的是(
A.摩擦力做功大小与力 F 的方向无关
B.合力做功大小与力 F 的方向有关
C.力 F 为水平方向时,F 做功为μmgx
D.力 F 做功的最小值为 max
解析:因合力做功为 max 且大小一定,而合力做的功等于力
F 与摩擦力 f 做功的代数和,而当 F sin θ=mg 时,摩擦力 f=0,
则此时摩擦力做功为零,此时力 F 做功最小,最小值为 max,D
正确.
答案:D
热点 2 功率的分析和计算
[热点归纳]
瞬时功率
的计算 P=Fvcos α,其中v为物体运动的瞬时速度,α为力的方向与瞬时速度方向的夹角
P=F·vF,其中vF为物体的速度v在力F方向上的分速度;P=Fv·v,其中Fv为物体受到的外力F在速度v方向上的分力
(续表)
考向 1 平均功率
【典题 3】(2023 年山东卷)《天工开物》中记载了古人借助
水力使用高转筒车往稻田里引水的场景(如图所示).引水过程简化
如下:两个半径均为 R 的水轮,以角速度ω匀速转动.水筒在筒车
上均匀排布,单位长度上有 n 个,与水轮间无相对滑动.每个水
筒离开水面时装有质量为 m 的水,其中的 60%被输送到高出水面
H 处灌入稻田.当地的重力加速度为 g,则筒车对灌入稻田的水做
功的功率为(
)
A.
2nmgω2RH
5
B.
3nmgωRH
5
3nmgω2RH
C.
5
D.nmgωRH
解析:每个水筒中水的重力为 G=mg,水筒的线速度为 v=
ωR,t 时间内,装水的水筒个数为 N=nvt=nωRt,筒车对灌入稻
答案:B
思路引导
本题为非质点模型,选取一个周期的时间,所有
的水筒及水均从最低点上升到最高点.
考向 2 瞬时功率
【典题4】(2024 年贵州卷)质量为 1 kg 的物块静置于光滑水
平地面上,设物块静止时的位置为 x 轴零点.现给物块施加一沿 x
轴正方向的水平力 F,其大小随位置x变化的关系如图所示,则物
块运动到 x=3 m 处,F 做功的瞬时功率为(
)
A.8 W
B.16 W
C.24 W
D.36 W
解析:根据图像可知物块运动到 x=3 m 处,F 做的总功为
得物块运动到 x=3 m 处时的速度为 v=4 m/s,故此时 F 做功的瞬
时功率为 P=Fv=8 W,A 正确.
答案:A
两种方式 以恒定功率启动 以恒定加速度启动
P t 图和
v t 图
热点 3 机车的启动运行
[热点归纳]
1.两种启动方式的比较.
(续表)
(续表)
=
率最大,但速度不是最大,v=
(1)无论哪种启动过程,机车的最大速度都等于其匀速运动时的
速度,即vm=
P P
Fmin F阻
(式中 Fmin 为最小牵引力,其值等于阻力 F阻).
(2)机车以恒定加速度启动的过程中,匀加速过程结束时,功
P P
F F阻
.
(3)机车以恒定功率启动时,牵引力做的功 W=Pt.由动能定理
得:Pt-F阻 x=ΔEk.此式经常用于求解机车以恒定功率启动过程的
位移大小.
【典题 5】(2023 年湖北卷)两节动车的额定功率分别为 P1 和
P2,在某平直铁轨上能达到的最大速度分别为 v1 和 v2.现将他们编
成动车组,设每节动车运行时受到的阻力在编组前后不变,则该
动车组在此铁轨上能达到的最大速度为(
)
答案:D
思路导引
动车组在此铁轨上达到最大速度时,动车组所受
合力为 0,阻力为两部分的阻力之和,牵引力为两部分的牵引力之
和.
变力做功的计算方法
求力做功时,一定要注意分析是求恒力做的功还是变力做的
功,如果是求变力做的功,还有以下 4 种方法.
方法 常见情境 方法概述
微元法 将物体的位移分割成许多小段,因小段很小,每一小段上作用在物体上的力可以视为恒力,这样就将变力做功转化为在无数个无穷小的位移方向上的恒力所做功的代数和.此法在中学阶段,常应用于求解大小不变、方向改变的变力做功问题
方法 常见情境 方法概述
平均
力法 在求解变力做功时,若物体受到的力方
向不变,而大小随位移呈线性变化,即
力均匀变化时,则可以认为物体受到一
F1+F2
大小为 F = 的恒力作用,F1 、F2
2
分别为物体初、末态所受到的力,然后
用公式 W=F lcos α求此力所做的功
(续表)
方法 常见情境 方法概述
图像法 在 F-x 图像中,图线与 x 轴所围“面积”
的代数和就表示力 F 在这段位移所做的
功,且位于 x 轴上方的“面积”为正,位
于 x 轴下方的“面积”为负,但此方法只
便于求图线所围图形规则的情况(如三角
形、矩形、圆等规则的几何图形)
(续表)
方法 常见情境 方法概述
等效转
换法 变力做功直接求解时,通常都比较复杂,
但若通过转换研究对象,有时可化为恒
力做功,用 W=Flcos ɑ求解. 此法常常应
用于轻绳通过定滑轮拉物体的问题中
恒力 F 把物块从 A 拉到 B,绳子对物块
(续表)
模型一 微元法
【典题 6】(2021 年山东济南质检)如图所示,一质量为m=
0.1 kg 的小方块(可视为质点)系在一伸直的轻绳一端,绳的另一
端固定在摩擦因数μ=0.2 的粗糙水平面上,绳长 r=1 m.给小方
以绳长为半径做圆周运动,重力加速度为 g 取 10 m/s2,当小方块
恰好运动一周时,绳子拉力为(
)
B.0.8π N
D.0.2π N
A.π N
C.0.4π N
答案:D
模型二 平均力法
【典题 7】当前,我国某些贫困地区的日常用水仍然依靠井水.
某同学用水桶从水井里提水,井内水面到井口的高度为 20 m.水桶
离开水面时,桶和水的总质量为 10 kg.由于水桶漏水,在被匀速提
升至井口的过程中,桶和水的总质量随着上升距离的变化而变化,
其关系如图所示.水桶可以看成质点,不计空气阻力,重力加速
度 g 取 10 m/s2.由图像可知,在提水的整个过程中,拉力对水
桶做的功为(
)
A.2000 J
B.1800 J
C.200 J
D.180 J
F1+F2
解析:由于水桶匀速上升,故拉力等于水桶重力.由于水和水
桶的质量随位移均匀减小.故拉力与位移满足线性关系,所以可用
平均力法求解变力做功.F1=m1g=100 N,F2=m2g=80 N,则拉力
2
x=1800 J.
做功为:W拉=
答案:B
模型三 图像法
【典题 8】一物体所受的力 F 随位移 x 变化的图像如图
)
所示,求在这一过程中,力 F 对物体做的功为(
A.3 J
B.6 J
C.7 J
D.8 J
解析:力 F 对物体做的功等于 x 轴上方梯形“面积”所表示
的正功与 x 轴下方三角形“面积”所表示的负功的代数之和.W1=
物体做的功为 W=7 J-1 J=6 J.B 正确.
答案:B
思路导引
力 F 随位移 x 变化的图像中,图像与坐标轴所围
成图形的面积等于力做的功,结合图像特点知,前 5 m 内力做的
功与前 3 m 内力做的功相同.
模型四 等效转换法
【典题 9】人在 A 点拉着绳通过一定滑轮吊起质量 m=50 kg
的物体,如图所示,开始时绳与水平方向的夹角为 60°.当人匀
速提起物体由 A 点沿水平方向运动 L=2 m 而到达 B 点时,绳与
水平方向成 30°角.则人对绳的拉力做了多少功?(g 取 10 m/s2)
解:人对绳的拉力做功与绳对物体的拉力做功是相同的,而
由于匀速提升物体,故物体处于平衡状态,可知绳上拉力 F=mg.
而物体上升的高度 h 等于右侧绳子的变化量ΔL,由几何关系得
解得ΔL≈1.46 m
所以,人对绳子做的功
W=mgΔL=500×1.46 J=730 J.
同课章节目录
