2025秋高考物理复习第五章第3节机械能守恒定律及其应用课件
文档属性
| 名称 | 2025秋高考物理复习第五章第3节机械能守恒定律及其应用课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-05 17:38:17 | ||
图片预览










文档简介
(共50张PPT)
第3节
机械能守恒定律及其应用
一、重力势能和弹性势能
1.重力势能.
路径
重力势能
(1)重力做功的特点.
①重力做功与________无关,只与初、末位置的高度差有关;
②重力做功引起物体__________的变化.
(2)重力势能.
举高
mgh
标量
①概念:物体由于被________而具有的能.
②表达式:Ep=________;
③矢标性:重力势能是________,正负表示其大小.
(3)重力做功与重力势能变化的关系.
减少
减少量
①定性关系:重力对物体做正功,重力势能就________;重
力对物体做负功,重力势能就增加;
②定量关系:重力对物体做的功等于物体重力势能的_______.
即 WG=-(Ep2-Ep1)=-ΔEp.
重力势能具有相对性,同一物体位于同一位置时,
由于选择不同的水平面作为零势能面,其重力势能的数值(包括正、
负)也不同.
越大
2.弹性势能:物体由于发生弹性形变而具有的能量.弹簧的弹
性势能的大小与形变量及劲度系数有关,弹簧的形变量________,
劲度系数越大,弹簧的弹性势能越大.
二、机械能守恒定律
1.机械能:________和势能统称为机械能.
2.机械能守恒定律的内容:在只有________或弹力做功的物体
系统内,动能与势能可以相互转化,而总的机械能保持不变.
3.机械能守恒定律的表达式:Ek1+Ep1=____________.
动能
重力
Ek2+Ep2
【基础自测】
1.判断下列题目的正误.
)
(1)被举到高处的物体的重力势能一定不为零.(
(2)物体克服重力做功,物体的重力势能一定增加.(
(3)任何发生弹性形变的物体都具有弹性势能.(
)
)
(4)弹力做正功弹性势能一定增加.(
)
(5)物体所受的合外力为零,物体的机械能一定守恒.(
)
答案:(1)× (2)√ (3)√ (4)× (5)×
2.(2023 年浙江卷)一位游客正在体验蹦极,绑上蹦极专用的橡
)
皮绳后从跳台纵身而下.游客从跳台下落直到最低点过程中(
A.弹性势能减小
B.重力势能减小
C.机械能保持不变
D.绳一绷紧动能就开始减小
答案:B
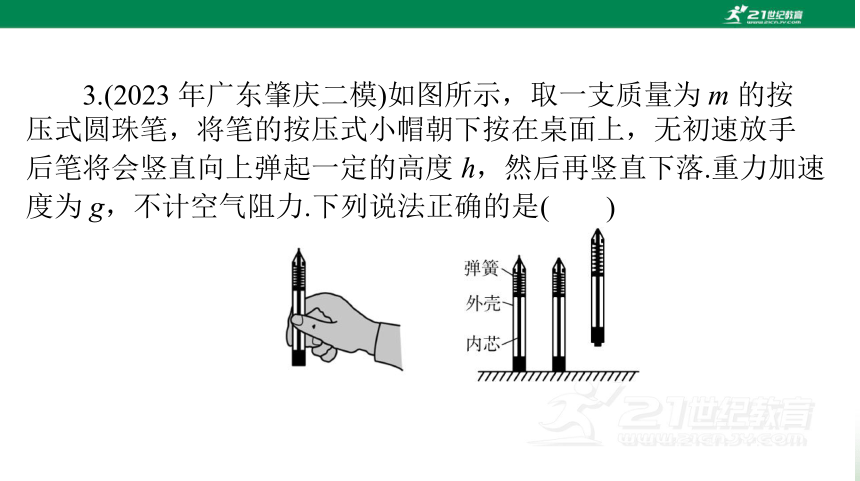
3.(2023 年广东肇庆二模)如图所示,取一支质量为 m 的按
压式圆珠笔,将笔的按压式小帽朝下按在桌面上,无初速放手
后笔将会竖直向上弹起一定的高度 h,然后再竖直下落.重力加速
)
度为 g,不计空气阻力.下列说法正确的是(
A.按压时笔内部弹簧的弹性势能增加了 mgh
B.放手后到笔向上离开桌面的过程弹簧的弹性势能全部转化
为笔的动能
C.笔在离开桌面后的上升阶段处于超重状态
D.笔从离开桌面到落回桌面过程的时间为
解析:因放手后笔将会竖直向上弹起一定的高度 h,该过程中
弹簧的弹性势能转化为重力势能,则弹性势能为 mgh,则按压时
笔内部弹簧的弹性势能增加了 mgh,A 正确.
答案:A
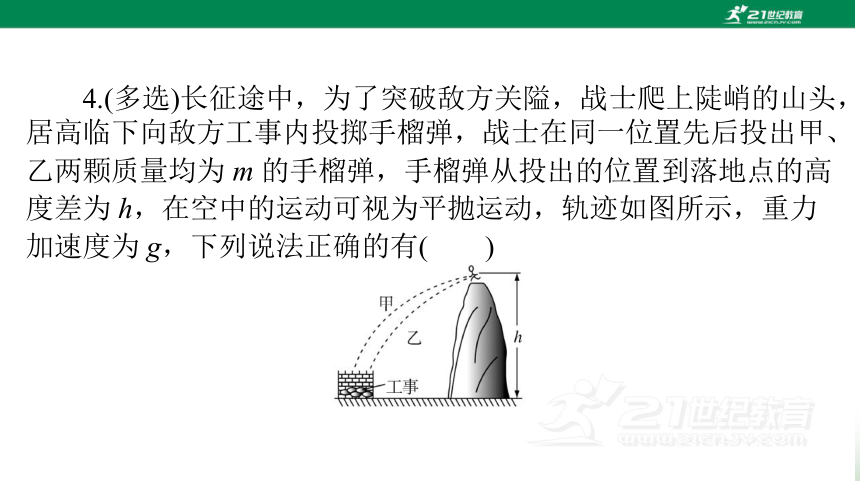
4.(多选)长征途中,为了突破敌方关隘,战士爬上陡峭的山头,
居高临下向敌方工事内投掷手榴弹,战士在同一位置先后投出甲、
乙两颗质量均为 m 的手榴弹,手榴弹从投出的位置到落地点的高
度差为 h,在空中的运动可视为平抛运动,轨迹如图所示,重力
加速度为 g,下列说法正确的有( )
A.甲在空中的运动时间比乙的长
B.两手榴弹在落地前瞬间,重力的功率相等
C.从投出到落地,每颗手榴弹的重力势能减少 mgh
D.从投出到落地,每颗手榴弹的机械能变化量为 mgh
答案:BC
热点 1 机械能守恒的判断方法
[热点归纳]
1.对机械能守恒条件的理解.
(1)物体的机械能是物体的势能加上动能,如果物体只受重力作用,
物体的机械能守恒,如果物体还受其他力作用,但其他力不做功或做
功代数和为零,则物体的机械能也守恒.
(2)物体和弹簧组成的系统的机械能包括物体的重力势能、物体的
动能和弹簧的弹性势能,如果只有重力和弹簧弹力做功,物体和弹簧
组成的系统机械能守恒.
2.机械能是否守恒的三种判断方法.
【典题 1】(多选)如图所示,下列关于机械能是否守恒
的判断正确的是(
)
甲
乙
丙
丁
A.图甲中,物体 A 将弹簧压缩的过程中,A 机械能守恒
B.图乙中,A 置于光滑水平面上,物体 B 沿光滑斜面下滑,
物体 B 机械能守恒
C.图丙中,不计任何阻力和定滑轮质量时 A 加速下落,B 加
速上升过程中,A、B 系统机械能守恒
D.图丁中,小球沿水平面做匀速圆锥摆运动时,小球的机械
能守恒
解析:图甲中重力和弹力做功,物体 A 和弹簧组成的系统机
械能守恒,但物体 A 机械能不守恒,A 错误;图乙中物体 B 除受重
力外,还受弹力,弹力对 B 做负功,机械能不守恒,但从能量特
点看 A、B 组成的系统机械能守恒,B 错误;图丙中绳子张力对 A
做负功,对 B 做正功,代数和为零,A、B 系统机械能守恒,C 正
确;图丁中小球的动能不变,势能不变,机械能守恒,D 正确.
答案:CD
易错提醒
(1)机械能守恒的条件绝不是合外力的功等于零,
更不是合外力为零;“只有重力做功”不等于“只受重力作用”.
(2)对于一些绳子突然绷紧、物体间碰撞等情况,除非题目特
别说明,否则机械能必定不守恒.
(3)对于系统机械能是否守恒,可以根据能量的转化进行判断.
热点 2 机械能守恒定律的应用
[热点归纳]
1.机械能守恒的三种表达式.
2.一般步骤.
【典题 2】(2022 年全国乙卷)如图所示,固定于竖直平
面内的光滑大圆环上套有一个小环.小环从大圆环
顶端 P 点由静止开始自由下滑,在下滑过程中,
)
小环的速率正比于(
A.它滑过的弧长
B.它下降的高度
C.它到 P 点的距离
D.它与 P 点的连线扫过的面积
解析:如图所示.设大圆环的半径为 R,小环
下降的高度为 h,它到 P 点的距离为 L,根据机
C 正确.
答案:C
思路导引
根据小环运动过程中机械能守恒,列出方程,求
出小环下滑过程中的速率,结合表达式判断与哪个选项符合.
【迁移拓展1】(2024 年全国甲卷)如图,一光滑大圆环固定在
竖直平面内,质量为 m 的小环套在大圆环上,小环从静止开始由
大圆环顶端经 Q 点自由下滑至其底部,Q 为竖直线与大圆环的切
)
点.则小环下滑过程中对大圆环的作用力大小(
A.在 Q 点最大
B.在 Q 点最小
C.先减小后增大
D.先增大后减小
解析:设大圆环半径为 R,小环在大圆环上某处(P 点)与圆环
的作用力恰好为零,如图所示.
设图中夹角为θ,从大圆环顶端到 P 点过程,根据机械能守
环圆心方向的分力大于小环所需的向心力,所以大圆环对小环的
弹力背离圆心,不断减小,从 P 点到最低点过程,小环速度变大,
小环重力和大圆环对小环的弹力合力提供向心力,所以大圆环对
小环的弹力逐渐变大,根据牛顿第三定律可知小环下滑过程中对
大圆环的作用力大小先减小后增大,C 正确.
答案:C
热点 3 含弹簧类机械能守恒问题
[热点归纳]
1.由于弹簧的形变会具有弹性势能,系统的总动能将发生变
化,若系统所受的外力和除弹簧弹力以外的内力不做功,系统机
械能守恒.
2.在相互作用过程特征方面,弹簧两端物体把弹簧拉伸至最长
(或压缩至最短)时,两端的物体具有相同的速度,弹性势能最大.
3.如果系统每个物体除弹簧弹力外所受合力为零,当弹簧为自
然长度时,系统内弹簧某一端的物体具有最大速度(如绷紧的弹簧
由静止释放).
【典题 3】(多选,2023 年广东广州开学考)如图所示,物体
A、B 通过细绳及轻质弹簧连接在轻滑轮两侧,物体 A、B 的质
量分别为 2m、m.开始时细绳伸直,用手托着物体 A 使弹簧处于
原长且 A 与地面的距离为 h,物体 B 静止在地面上,放手后物体
A 下落,与地面即将接触时速度大小为 v,此时物体 B 对地面恰
好无压力,不计一切摩擦及空气阻力,重力加速度大小为 g,则下
列说法中正确的是(
)
A.物体 A 下落过程中,物体 A 和弹簧组成
的系统机械能守恒
解析:由题可知,物体 A 下落过程中,物体 B 一直静止不动,
对于物体 A 和弹簧组成的系统,只有重力和弹簧弹力做功,则物
体 A 和弹簧组成的系统机械能守恒,A 正确;物体 A 与地面即将接
触时,物体 B 对地面恰好无压力,则此时弹簧的弹力为 T=mg,
开始时弹簧处于原长,由胡克定律知 T=kh,联立解得弹簧的劲度
细绳对 A 的拉力也等于 mg ,对 A 根据牛顿第二定律得 2mg -
答案:AC
思路导引
弹簧的初状态是处于原长、弹性势能为零,末状
态根据“物体 B 对地面恰好无压力”可求,进而求得弹性势能和
弹簧的弹力.根据运动过程中物体 A、B 及弹簧组成的系统机械能
守恒可分析 D 选项.
【迁移拓展 2】如图所示,三个小球 A、B、C 的质量均为
m,A 与 B、C 间通过铰链用轻杆连接,杆长为 L,B、C 置
于水平地面上,用一轻质弹簧连接,弹簧处于原
长.现 A 由静止释放下降到最低点,两轻杆间夹
角α由 60°变为 120°,A、B、C 在同一竖直平
面内运动,弹簧在弹性限度内,忽略一切摩擦,
重力加速度为 g.则此下降过程中(
)
A.释放 A 的瞬间,B 受到地面的支持力等于 1.5mg
B.A 的动能最大时,B 受到地面的支持力等于 1.5mg
C.弹簧的弹性势能最大时,A 的加速度等于 0
D.弹簧的弹性势能最大值和系统动能的最大值相同
解析:A 的动能最大时,设 B 和 C 受到地面的支持力大小均
为 F,此时整体在竖直方向上受力平衡,得 2F=3mg,所以 F=
1.5mg,B 正确.释放 A 的瞬间,A有向下的加速度,处于失重状态,
所以 B 受到地面的支持力小于 1.5mg, A 错误;当 A 到达最低点
时,动能为零,此时弹簧的弹性势能最大,A 的加速度方向向上,
C 错误;当弹性势能最大时,系统的动能为零,小球 A 减少的重
力势能全部转化为弹簧的弹性势能,当系统的动能最大时,小球
A 还没到最低点,并且是将小球 A 减少的重力势能转化为系统的
动能和弹簧的弹性势能,故弹簧的弹性势能最大值大于系统动能
的最大值,D 错误.
答案:B
机械能守恒定律在绳(杆)连接体模型中的应用
多个物体机械能守恒问题:根据物体间的关联方式,常见“轻
绳连接”和“轻杆连接”两种类型.
模型特点 通过轻绳连接的两个物体速度大小相等
常见情景
模型提醒 如图所示的两物体组成的系统,在释放 B 而使 A、B
运动的过程中,A、B的速度均沿绳子方向,在相等的
时间内 A、B 运动的路程相等,则 A、B 的速率相等
模型一 “轻绳连接”的多物体系统
【典题 4】(多选,2022 年河北卷)如图,轻质定滑轮固定
在天花板上,物体 P 和 Q 用不可伸长的轻绳相连,悬挂在定滑
轮上,质量 mQ>mP,t=0时刻将两物体由静止释放,物体 Q 的加
物体 Q 释放位置处于同一高度,取 t=0 时刻物体 P 所在水平面为
零势能面,此时物体 Q 的机械能为 E.重力加速度大小为 g,不计
摩擦和空气阻力,两物体均可视为质点.下列说法正确的是(
)
A.物体 P 和 Q 的质量之比为 1∶3
答案:BCD
模型特点 通过轻绳连接的两个物体速度大小不等
常见情景
模型提醒 如图所示,A 放在光滑斜面上,B 穿过竖直光滑杆 PQ 下滑,将 B 的速度 v 沿绳子方向和垂直绳子方向分解,如图所示,其中沿绳子方向的分速度 vx 与 A 的速度大小相等 B物体的速度大小总是 A 的 2 倍
【典题 5】(多选,2021 年福建厦门模拟)如图所示,质量
均为 m 的物块 A 和 B用不可伸长的轻绳连接,A放在倾角为 θ 的
固定光滑斜面上,而 B 能沿光滑竖直杆上下滑动,杆和滑轮中心
间的距离为 L,物块 B 从与滑轮等高处由静止开始下落,斜面与
杆足够长,重力加速度为 g.在物块 B 下落到绳与水平方向的夹角
为θ的过程中,下列说法正确的是(
)
A.开始下落时,B 的加速度大于 g
B.物块 B 的重力势能减小量为 mgLtan θ
C.物块 A 的速度小于物块 B 的速度
解析:刚开始下落时,绳子的拉力方向沿水平方向,竖直方向上
只受重力,所以加速度为 g,故A错误;B 下降的高度为 h=Ltan θ,故
物块 B 减小的重力势能为ΔEp=mgLtan θ,B 正确;将 B 的速度分解为
沿绳方向的速度和垂直绳方向的速度,则 vA=v绳=vBsin θ,则物块 A
的速度小于物块 B 的速度,故 C 正确;系统机械能守恒,故 mgLtan θ-
答案:BC
思路导引
判断出开始下落时,加速度在哪个方向,即可分
析 A 选项.据图中三角形求出 B 下落高度,B 选项得以解决.A 的速
度是 B 速度的一个分速度,B 的速度是矩形的对角线,A 的速度
是一直角边,二者速度大小关系可明确.根据 A 与 B 减少的重力势
能等于二者增加的动能之和,列方程可分析 D 选项.
常见
情景
模型
提醒 (1)平动时两物体线速度相等,转动时两物体角
速度相等.
(2)杆对物体的作用力并不总是沿杆的方向,杆
能对物体做功,单个物体机械能不守恒.
(3)对于杆和球组成的系统,忽略空气阻力和各
种摩擦且没有其他力对系统做功,则系统机械
能守恒.杆对两个物体做的功互为相反数 两球沿杆方向的速度大小
相等
v杆=vacos θ
而 v杆=vbsin θ
va
解得 vb=
tan θ
模型二 “轻杆连接”的多物体系统
【典题 6】(多选)如图 所示,一根长为 3L 的轻杆可绕
水平转轴 O 转动,两端固定质量均为 m 的小球 A
和 B,A 到 O 的距离为 L,现使杆在竖直平面内转
动,B 运动到最高点时,恰好对杆无作用力,两球
均视为质点,不计空气阻力和摩擦阻力,重力加速
度为 g.当 B 由最高点第一次转至与 O 点等高的过
程中,下列说法正确的是(
)
A.杆对 B 球做负功
B.B 球的机械能守恒
解析:当 B 由最高点第一次转至与 O 点等高的过程中,对于
两球组成的系统机械能守恒,只有重力做功,所以系统的机械能
守恒.A 球的动能和重力势能均增加,则 A 球的机械能增加,根据
系统的机械能守恒知 B 球的机械能减少,由功能关系知杆对 B 球
做负功,A 正确,B 错误;B 球在最高点时,由重力提供向心力,
答案:AD
模型三 链条类
【典题 7】(2022 年重庆模拟)如图所示,总长为 L,质量分
布均匀的铁链放在高度为 H 的光滑桌面上,有长度为 a 的一段下
垂,H>L,重力加速度为 g,则铁链刚接触地面时速度为( )
解析:设铁链单位长度的质量为 m,设地面为零势能面,由
答案:D
第3节
机械能守恒定律及其应用
一、重力势能和弹性势能
1.重力势能.
路径
重力势能
(1)重力做功的特点.
①重力做功与________无关,只与初、末位置的高度差有关;
②重力做功引起物体__________的变化.
(2)重力势能.
举高
mgh
标量
①概念:物体由于被________而具有的能.
②表达式:Ep=________;
③矢标性:重力势能是________,正负表示其大小.
(3)重力做功与重力势能变化的关系.
减少
减少量
①定性关系:重力对物体做正功,重力势能就________;重
力对物体做负功,重力势能就增加;
②定量关系:重力对物体做的功等于物体重力势能的_______.
即 WG=-(Ep2-Ep1)=-ΔEp.
重力势能具有相对性,同一物体位于同一位置时,
由于选择不同的水平面作为零势能面,其重力势能的数值(包括正、
负)也不同.
越大
2.弹性势能:物体由于发生弹性形变而具有的能量.弹簧的弹
性势能的大小与形变量及劲度系数有关,弹簧的形变量________,
劲度系数越大,弹簧的弹性势能越大.
二、机械能守恒定律
1.机械能:________和势能统称为机械能.
2.机械能守恒定律的内容:在只有________或弹力做功的物体
系统内,动能与势能可以相互转化,而总的机械能保持不变.
3.机械能守恒定律的表达式:Ek1+Ep1=____________.
动能
重力
Ek2+Ep2
【基础自测】
1.判断下列题目的正误.
)
(1)被举到高处的物体的重力势能一定不为零.(
(2)物体克服重力做功,物体的重力势能一定增加.(
(3)任何发生弹性形变的物体都具有弹性势能.(
)
)
(4)弹力做正功弹性势能一定增加.(
)
(5)物体所受的合外力为零,物体的机械能一定守恒.(
)
答案:(1)× (2)√ (3)√ (4)× (5)×
2.(2023 年浙江卷)一位游客正在体验蹦极,绑上蹦极专用的橡
)
皮绳后从跳台纵身而下.游客从跳台下落直到最低点过程中(
A.弹性势能减小
B.重力势能减小
C.机械能保持不变
D.绳一绷紧动能就开始减小
答案:B
3.(2023 年广东肇庆二模)如图所示,取一支质量为 m 的按
压式圆珠笔,将笔的按压式小帽朝下按在桌面上,无初速放手
后笔将会竖直向上弹起一定的高度 h,然后再竖直下落.重力加速
)
度为 g,不计空气阻力.下列说法正确的是(
A.按压时笔内部弹簧的弹性势能增加了 mgh
B.放手后到笔向上离开桌面的过程弹簧的弹性势能全部转化
为笔的动能
C.笔在离开桌面后的上升阶段处于超重状态
D.笔从离开桌面到落回桌面过程的时间为
解析:因放手后笔将会竖直向上弹起一定的高度 h,该过程中
弹簧的弹性势能转化为重力势能,则弹性势能为 mgh,则按压时
笔内部弹簧的弹性势能增加了 mgh,A 正确.
答案:A
4.(多选)长征途中,为了突破敌方关隘,战士爬上陡峭的山头,
居高临下向敌方工事内投掷手榴弹,战士在同一位置先后投出甲、
乙两颗质量均为 m 的手榴弹,手榴弹从投出的位置到落地点的高
度差为 h,在空中的运动可视为平抛运动,轨迹如图所示,重力
加速度为 g,下列说法正确的有( )
A.甲在空中的运动时间比乙的长
B.两手榴弹在落地前瞬间,重力的功率相等
C.从投出到落地,每颗手榴弹的重力势能减少 mgh
D.从投出到落地,每颗手榴弹的机械能变化量为 mgh
答案:BC
热点 1 机械能守恒的判断方法
[热点归纳]
1.对机械能守恒条件的理解.
(1)物体的机械能是物体的势能加上动能,如果物体只受重力作用,
物体的机械能守恒,如果物体还受其他力作用,但其他力不做功或做
功代数和为零,则物体的机械能也守恒.
(2)物体和弹簧组成的系统的机械能包括物体的重力势能、物体的
动能和弹簧的弹性势能,如果只有重力和弹簧弹力做功,物体和弹簧
组成的系统机械能守恒.
2.机械能是否守恒的三种判断方法.
【典题 1】(多选)如图所示,下列关于机械能是否守恒
的判断正确的是(
)
甲
乙
丙
丁
A.图甲中,物体 A 将弹簧压缩的过程中,A 机械能守恒
B.图乙中,A 置于光滑水平面上,物体 B 沿光滑斜面下滑,
物体 B 机械能守恒
C.图丙中,不计任何阻力和定滑轮质量时 A 加速下落,B 加
速上升过程中,A、B 系统机械能守恒
D.图丁中,小球沿水平面做匀速圆锥摆运动时,小球的机械
能守恒
解析:图甲中重力和弹力做功,物体 A 和弹簧组成的系统机
械能守恒,但物体 A 机械能不守恒,A 错误;图乙中物体 B 除受重
力外,还受弹力,弹力对 B 做负功,机械能不守恒,但从能量特
点看 A、B 组成的系统机械能守恒,B 错误;图丙中绳子张力对 A
做负功,对 B 做正功,代数和为零,A、B 系统机械能守恒,C 正
确;图丁中小球的动能不变,势能不变,机械能守恒,D 正确.
答案:CD
易错提醒
(1)机械能守恒的条件绝不是合外力的功等于零,
更不是合外力为零;“只有重力做功”不等于“只受重力作用”.
(2)对于一些绳子突然绷紧、物体间碰撞等情况,除非题目特
别说明,否则机械能必定不守恒.
(3)对于系统机械能是否守恒,可以根据能量的转化进行判断.
热点 2 机械能守恒定律的应用
[热点归纳]
1.机械能守恒的三种表达式.
2.一般步骤.
【典题 2】(2022 年全国乙卷)如图所示,固定于竖直平
面内的光滑大圆环上套有一个小环.小环从大圆环
顶端 P 点由静止开始自由下滑,在下滑过程中,
)
小环的速率正比于(
A.它滑过的弧长
B.它下降的高度
C.它到 P 点的距离
D.它与 P 点的连线扫过的面积
解析:如图所示.设大圆环的半径为 R,小环
下降的高度为 h,它到 P 点的距离为 L,根据机
C 正确.
答案:C
思路导引
根据小环运动过程中机械能守恒,列出方程,求
出小环下滑过程中的速率,结合表达式判断与哪个选项符合.
【迁移拓展1】(2024 年全国甲卷)如图,一光滑大圆环固定在
竖直平面内,质量为 m 的小环套在大圆环上,小环从静止开始由
大圆环顶端经 Q 点自由下滑至其底部,Q 为竖直线与大圆环的切
)
点.则小环下滑过程中对大圆环的作用力大小(
A.在 Q 点最大
B.在 Q 点最小
C.先减小后增大
D.先增大后减小
解析:设大圆环半径为 R,小环在大圆环上某处(P 点)与圆环
的作用力恰好为零,如图所示.
设图中夹角为θ,从大圆环顶端到 P 点过程,根据机械能守
环圆心方向的分力大于小环所需的向心力,所以大圆环对小环的
弹力背离圆心,不断减小,从 P 点到最低点过程,小环速度变大,
小环重力和大圆环对小环的弹力合力提供向心力,所以大圆环对
小环的弹力逐渐变大,根据牛顿第三定律可知小环下滑过程中对
大圆环的作用力大小先减小后增大,C 正确.
答案:C
热点 3 含弹簧类机械能守恒问题
[热点归纳]
1.由于弹簧的形变会具有弹性势能,系统的总动能将发生变
化,若系统所受的外力和除弹簧弹力以外的内力不做功,系统机
械能守恒.
2.在相互作用过程特征方面,弹簧两端物体把弹簧拉伸至最长
(或压缩至最短)时,两端的物体具有相同的速度,弹性势能最大.
3.如果系统每个物体除弹簧弹力外所受合力为零,当弹簧为自
然长度时,系统内弹簧某一端的物体具有最大速度(如绷紧的弹簧
由静止释放).
【典题 3】(多选,2023 年广东广州开学考)如图所示,物体
A、B 通过细绳及轻质弹簧连接在轻滑轮两侧,物体 A、B 的质
量分别为 2m、m.开始时细绳伸直,用手托着物体 A 使弹簧处于
原长且 A 与地面的距离为 h,物体 B 静止在地面上,放手后物体
A 下落,与地面即将接触时速度大小为 v,此时物体 B 对地面恰
好无压力,不计一切摩擦及空气阻力,重力加速度大小为 g,则下
列说法中正确的是(
)
A.物体 A 下落过程中,物体 A 和弹簧组成
的系统机械能守恒
解析:由题可知,物体 A 下落过程中,物体 B 一直静止不动,
对于物体 A 和弹簧组成的系统,只有重力和弹簧弹力做功,则物
体 A 和弹簧组成的系统机械能守恒,A 正确;物体 A 与地面即将接
触时,物体 B 对地面恰好无压力,则此时弹簧的弹力为 T=mg,
开始时弹簧处于原长,由胡克定律知 T=kh,联立解得弹簧的劲度
细绳对 A 的拉力也等于 mg ,对 A 根据牛顿第二定律得 2mg -
答案:AC
思路导引
弹簧的初状态是处于原长、弹性势能为零,末状
态根据“物体 B 对地面恰好无压力”可求,进而求得弹性势能和
弹簧的弹力.根据运动过程中物体 A、B 及弹簧组成的系统机械能
守恒可分析 D 选项.
【迁移拓展 2】如图所示,三个小球 A、B、C 的质量均为
m,A 与 B、C 间通过铰链用轻杆连接,杆长为 L,B、C 置
于水平地面上,用一轻质弹簧连接,弹簧处于原
长.现 A 由静止释放下降到最低点,两轻杆间夹
角α由 60°变为 120°,A、B、C 在同一竖直平
面内运动,弹簧在弹性限度内,忽略一切摩擦,
重力加速度为 g.则此下降过程中(
)
A.释放 A 的瞬间,B 受到地面的支持力等于 1.5mg
B.A 的动能最大时,B 受到地面的支持力等于 1.5mg
C.弹簧的弹性势能最大时,A 的加速度等于 0
D.弹簧的弹性势能最大值和系统动能的最大值相同
解析:A 的动能最大时,设 B 和 C 受到地面的支持力大小均
为 F,此时整体在竖直方向上受力平衡,得 2F=3mg,所以 F=
1.5mg,B 正确.释放 A 的瞬间,A有向下的加速度,处于失重状态,
所以 B 受到地面的支持力小于 1.5mg, A 错误;当 A 到达最低点
时,动能为零,此时弹簧的弹性势能最大,A 的加速度方向向上,
C 错误;当弹性势能最大时,系统的动能为零,小球 A 减少的重
力势能全部转化为弹簧的弹性势能,当系统的动能最大时,小球
A 还没到最低点,并且是将小球 A 减少的重力势能转化为系统的
动能和弹簧的弹性势能,故弹簧的弹性势能最大值大于系统动能
的最大值,D 错误.
答案:B
机械能守恒定律在绳(杆)连接体模型中的应用
多个物体机械能守恒问题:根据物体间的关联方式,常见“轻
绳连接”和“轻杆连接”两种类型.
模型特点 通过轻绳连接的两个物体速度大小相等
常见情景
模型提醒 如图所示的两物体组成的系统,在释放 B 而使 A、B
运动的过程中,A、B的速度均沿绳子方向,在相等的
时间内 A、B 运动的路程相等,则 A、B 的速率相等
模型一 “轻绳连接”的多物体系统
【典题 4】(多选,2022 年河北卷)如图,轻质定滑轮固定
在天花板上,物体 P 和 Q 用不可伸长的轻绳相连,悬挂在定滑
轮上,质量 mQ>mP,t=0时刻将两物体由静止释放,物体 Q 的加
物体 Q 释放位置处于同一高度,取 t=0 时刻物体 P 所在水平面为
零势能面,此时物体 Q 的机械能为 E.重力加速度大小为 g,不计
摩擦和空气阻力,两物体均可视为质点.下列说法正确的是(
)
A.物体 P 和 Q 的质量之比为 1∶3
答案:BCD
模型特点 通过轻绳连接的两个物体速度大小不等
常见情景
模型提醒 如图所示,A 放在光滑斜面上,B 穿过竖直光滑杆 PQ 下滑,将 B 的速度 v 沿绳子方向和垂直绳子方向分解,如图所示,其中沿绳子方向的分速度 vx 与 A 的速度大小相等 B物体的速度大小总是 A 的 2 倍
【典题 5】(多选,2021 年福建厦门模拟)如图所示,质量
均为 m 的物块 A 和 B用不可伸长的轻绳连接,A放在倾角为 θ 的
固定光滑斜面上,而 B 能沿光滑竖直杆上下滑动,杆和滑轮中心
间的距离为 L,物块 B 从与滑轮等高处由静止开始下落,斜面与
杆足够长,重力加速度为 g.在物块 B 下落到绳与水平方向的夹角
为θ的过程中,下列说法正确的是(
)
A.开始下落时,B 的加速度大于 g
B.物块 B 的重力势能减小量为 mgLtan θ
C.物块 A 的速度小于物块 B 的速度
解析:刚开始下落时,绳子的拉力方向沿水平方向,竖直方向上
只受重力,所以加速度为 g,故A错误;B 下降的高度为 h=Ltan θ,故
物块 B 减小的重力势能为ΔEp=mgLtan θ,B 正确;将 B 的速度分解为
沿绳方向的速度和垂直绳方向的速度,则 vA=v绳=vBsin θ,则物块 A
的速度小于物块 B 的速度,故 C 正确;系统机械能守恒,故 mgLtan θ-
答案:BC
思路导引
判断出开始下落时,加速度在哪个方向,即可分
析 A 选项.据图中三角形求出 B 下落高度,B 选项得以解决.A 的速
度是 B 速度的一个分速度,B 的速度是矩形的对角线,A 的速度
是一直角边,二者速度大小关系可明确.根据 A 与 B 减少的重力势
能等于二者增加的动能之和,列方程可分析 D 选项.
常见
情景
模型
提醒 (1)平动时两物体线速度相等,转动时两物体角
速度相等.
(2)杆对物体的作用力并不总是沿杆的方向,杆
能对物体做功,单个物体机械能不守恒.
(3)对于杆和球组成的系统,忽略空气阻力和各
种摩擦且没有其他力对系统做功,则系统机械
能守恒.杆对两个物体做的功互为相反数 两球沿杆方向的速度大小
相等
v杆=vacos θ
而 v杆=vbsin θ
va
解得 vb=
tan θ
模型二 “轻杆连接”的多物体系统
【典题 6】(多选)如图 所示,一根长为 3L 的轻杆可绕
水平转轴 O 转动,两端固定质量均为 m 的小球 A
和 B,A 到 O 的距离为 L,现使杆在竖直平面内转
动,B 运动到最高点时,恰好对杆无作用力,两球
均视为质点,不计空气阻力和摩擦阻力,重力加速
度为 g.当 B 由最高点第一次转至与 O 点等高的过
程中,下列说法正确的是(
)
A.杆对 B 球做负功
B.B 球的机械能守恒
解析:当 B 由最高点第一次转至与 O 点等高的过程中,对于
两球组成的系统机械能守恒,只有重力做功,所以系统的机械能
守恒.A 球的动能和重力势能均增加,则 A 球的机械能增加,根据
系统的机械能守恒知 B 球的机械能减少,由功能关系知杆对 B 球
做负功,A 正确,B 错误;B 球在最高点时,由重力提供向心力,
答案:AD
模型三 链条类
【典题 7】(2022 年重庆模拟)如图所示,总长为 L,质量分
布均匀的铁链放在高度为 H 的光滑桌面上,有长度为 a 的一段下
垂,H>L,重力加速度为 g,则铁链刚接触地面时速度为( )
解析:设铁链单位长度的质量为 m,设地面为零势能面,由
答案:D
同课章节目录
