2025秋高考物理复习第四章第4节万有引力定律及其应用课件
文档属性
| 名称 | 2025秋高考物理复习第四章第4节万有引力定律及其应用课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-05 17:38:17 | ||
图片预览











文档简介
(共44张PPT)
第4节
万有引力定律及其应用
一、开普勒三定律
椭圆
1. 开普勒第一定律:所有的行星围绕太阳运动的轨道都是
________,太阳处在所有椭圆的一个焦点上.
2.开普勒第二定律:行星与太阳的连线在相同的时间内_____
________相等.
的面积
公转周期的二次方
3. 开普勒第三定律:所有行星的轨道的半长轴的三次方与
____________________的比值都相等.
扫过
r2
二、万有引力定律
质量的乘积
1.内容:自然界中任何两个物体都是互相吸引的,引力的大小
跟这两个物体的_____________成正比,跟它们的距离的二次方成
反比.
6.67×10-11 N·m2/kg2
质点
2.公式:F=G
m1m2
,其中 G=__________________,叫引力
常量,由英国物理学家卡文迪什利用扭秤装置第一次测得.
3.适用条件:公式适用于________间的相互作用.均匀的球体
也可视为质量集中于球心的质点,r 是两球心间的距离.
宇宙速度 数值(km/s) 意义
第一宇宙速度
(环绕速度) ①________ 是人造地球卫星的最②____发射速度,也是人造地球卫星绕地球做圆周运动的最③____速度
第二宇宙速度 ④________ 使物体挣脱⑤____引力束缚的最小发射速度
第三宇宙速度 ⑥________ 使物体挣脱⑦____引力束缚的最小发射速度
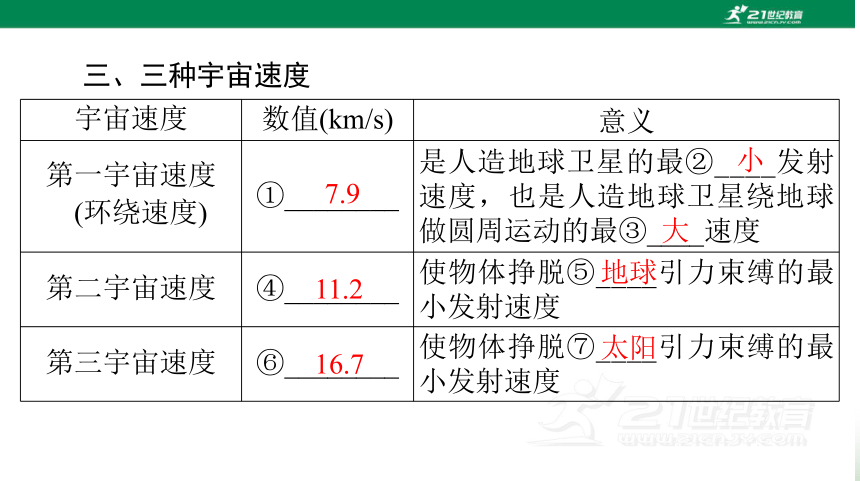
三、三种宇宙速度
7.9
小
大
11.2
地球
16.7
太阳
四、同步卫星
静止
24 h
1.概念:相对地面________的卫星称为同步卫星.
2.基本特征:①周期为地球自转周期 T=________;②轨道在
赤道平面内;③运动的角速度与地球的自转角速度相同;④高度 h
一定;⑤轨道和地球赤道为共面同心圆;⑥卫星运行速度一定.
【基础自测】
1.判断下列题目的正误.
(1)行星在椭圆轨道上运行速率是变化的,离太阳越远,运行
速率越大.(
)
(2)牛顿总结了前人的科研成果,在此基础上,经过研究得出
了万有引力定律.(
)
(3)牛顿利用扭秤实验装置比较准确地测出了引力常量.(
)
(4) 第一宇宙速度是卫星绕地球做匀速圆周运动的最小速
度.(
)
(5)若物体的速度大于第二宇宙速度而小于第三宇宙速度,则
物体可绕太阳运行.(
)
答案:(1)× (2)√ (3)× (4)× (5)√
2.(多选)如图所示,一颗卫星绕地球做椭圆运动,运动周期
为 T,图中虚线为卫星的运动轨迹,A、B、C、D 是轨迹上的四
个位置,其中 A 距离地球最近,C 距离地球最远.B 点和 D 点是
)
弧线 ABC 和 ADC 的中点,下列说法正确的是(
A.卫星在 A 点的速度最大
B.卫星在 C 点的加速度最大
答案:AC
3.(2022 年河北卷)2008 年,我国天文学家利用国家天文台兴
隆观测基地的 2.16 米望远镜,发现了一颗绕恒星 HD173416 运动
的系外行星 HD173416b,2019 年,该恒星和行星被国际天文学联
合会分别命名为“羲和”和“望舒”,天文观测得到恒星“羲
和”的质量是太阳质量的 2 倍,若将“望舒”与地球的公转均视
为匀速圆周运动,且公转的轨道半径相等.则望舒与地球公转速度
大小的比值为(
)
解析:地球绕太阳公转和行星“望舒”绕恒星“羲和”的匀
答案:C
4.(2024 年贵州卷)土星的部分卫星绕土星的运动可视为匀速
圆周运动,其中的两颗卫星轨道半径分别为r1、r2 且 r1≠r2,向
心加速度大小分别为 a1、a2,则(
)
答案:D
热点 1 万有引力与重力的关系
考向 1 考虑星球自转时,星球表面万有引力与重力的关系
[热点归纳]
地球对物体的万有引力 F 表现为两个效果:一是重力 mg,
二是提供物体随地球自转的向心力 F向,如图所示.
【典题 1】(2022 年广东广州模拟)现实版的倒霉熊乔伊曾因为
白化病两次被送到北极,还有一次被送到位于赤道的北极馆.若乔
伊质量始终为 m,它在北极和北极馆的重力差为ΔN,地球半径 R,
则可求出同步卫星运动的周期为(
)
答案:B
考向 2 不考虑星球自转时,星球表面万有引力与重力的关系
[热点归纳]
因为一般星球自转表面需要的向心力远小于重力,所以不研
【典题 2】质量为 m 的着陆器在着陆火星前,会在火星表面
附近经历一个时长为 t0、速度由 v0 减速到零的过程.已知火星的质
量约为地球的 0.1 倍,半径约为地球的 0.5 倍,地球表面的重力加
速度大小为 g,忽略火星大气阻力.若该减速过程可视为一个竖直
向下的匀减速直线运动,此过程中着陆器受到的制动力大小约为
(
)
答案:B
考向 3 天体表面某深度处的重力加速度
①推论 1:在匀质球壳的空腔内任意位置处,质点受到球壳的
万有引力的合力为零,即∑F引=0.
②推论 2:在匀质球体内部距离球心 r 处的质点(m)受到的万
有引力等于球体内半径为 r 的同心球体(M′)对其的万有引力,即
【典题 3】(2023 年海南海口三模)已知某星球的半径为 R,该
星球表面处的重力加速度大小为 g,不考虑星球的自转,则距离星
球表面高度为 3R 处的重力加速度大小为(
)
1
A. g
3
1
B. g
4
1
C. g
9
1
D. g
16
答案:D
热点 2 中心天体质量和密度的计算
[热点归纳]
天体质量和密度常用的估算方法.
(续表)
【典题4】(2024 年河南卷)天文学家发现,在太阳系外的一颗
红矮星有两颗行星绕其运行,其中行星 GJ1002c 的轨道近似为圆,
轨道半径约为日地距离的 0.07 倍,周期约为 0.06 年,则这颗红矮
)
星的质量约为太阳质量的(
A.0.001 倍
C.10 倍
B.0.1 倍
D.1000 倍
答案:B
方法技巧 估算天体质量和密度的四点注意
(1)利用万有引力提供天体圆周运动的向心力估算天体质量
时,估算的只是中心天体的质量,而非环绕天体的质量.
(2)区别天体半径 R 和卫星轨道半径 r,只有在天体表面附近
中心天体的半径.
(3)天体质量估算中常有隐含条件,如地球的自转周期为 24 h,
公转周期为 365 天等.
(4)注意黄金代换式 GM=gR2 的应用.
热点 3 卫星
[热点归纳]
地球卫星的运行参数.
(续表)
【典题 5】(2022 年广东卷)“祝融号”火星车需要“休眠”以
度过火星寒冷的冬季.假设火星和地球的冬季是各自公转周期的四
分之一,且火星的冬季时长约为地球的 1.88 倍.火星和地球绕太阳
的公转均可视为匀速圆周运动.下列关于火星、地球公转的说法正
确的是(
)
A.火星公转的线速度比地球的大
B.火星公转的角速度比地球的大
C.火星公转的半径比地球的小
D.火星公转的加速度比地球的小
答案:D
热点 4 宇宙速度
[热点归纳]
1.第一宇宙速度的推导
2.宇宙速度与运动轨迹的关系
(1)v发=7.9 km/s 时,卫星绕地球做匀速圆周运动.
(2)7.9 km/s<v发<11.2 km/s,卫星绕地球运动的轨迹为椭圆.
(3)11.2 km/s<v发<16.7 km/s,卫星绕太阳做椭圆运动.
(4)v发≥16.7 km/s,卫星将挣脱太阳引力的束缚,飞到太阳系
以外的空间.
【典题6】(多选,2024 年湖南卷)2024 年 5 月 3 日,“嫦娥
六号”探测器顺利进入地月转移轨道,正式开启月球之旅.相较于
“嫦娥四号”和“嫦娥五号”,本次的主要任务是登陆月球背面
进行月壤采集并通过升空器将月壤转移至绕月运行的返回舱,返
回舱再通过返回轨道返回地球.设返回舱绕月运行的轨道为圆轨
道,半径近似为月球半径.已知月球表面重力加速度约为地球表面
动,下列说法正确的是(
)
A.其相对于月球的速度大于地球第一宇宙速度
B.其相对于月球的速度小于地球第一宇宙速度
答案:BD
情景图 “双星”模型 “三星”模型 “四星”模型
“双星”和“三星”模型分析
“双星”“三星”和“四星”模型.
运动
特点 转动方向、周期、角速度相同,运动半径一般不等 转动方向、周期、角速度、线速度大小均相同,圆周运动半径相等 转动方向、周期、角速度、线速度大小均相同,圆周运动半径相等
受力
特点 两星间的万有引力提供两星圆周运动的向心力 各星所受万有引力的合力提供圆周运动的向心力 各星所受万有引力的合力提供圆周运动的向心力
(续表)
(续表)
【典题 7】(多选,2023 年海南海口一模)冥王星与其附近的另
一星体“卡戎”可视为双星系统,质量之比约为 7∶1,同时绕它
们连线上某点 O 做匀速圆周运动.由此可知(
)
A.冥王星的轨道半径约为“卡戎”的
1
7
B.冥王星的向心加速度大小约为“卡戎”的 7 倍
D.冥王星的动能约为“卡戎”的 7 倍
解析:冥王星 M 与“卡戎”m 组成双星系统,所以冥王星和
“卡戎”周期是相等的,角速度也是相等的.它们之间的万有引力
提供各自的向心力,则有 Mr1ω2=mr2ω2,解得 r1∶r2=m∶M=
1∶7,A 正确;根据向心加速度公式 an=ω2r 可知,两者的向心加
速度之比 an1∶an2=r1∶r2 =1∶7,B 错误;根据线速度 v=ωr 可得,
两者的线速度大小之比 v1∶v2=r1∶r2 =1∶7,C 正确;由万有引力
r1∶r2=1∶7,D 错误.
答案:AC
【触类旁通】(2022 年广东模拟)三颗质量相等的恒星彼此连
线恰好构成等边三角形,忽略其他星体对其引力,测量星体之间
距离,并通过理论计算得到该三星系统的周期为 T,但实际观测中
得到该三星系统周期为 nT,科学家猜测在三星构成的等边三角形
的中心存在质量为 M 的黑洞,该黑洞质量是恒星质量的(
)
答案:D
第4节
万有引力定律及其应用
一、开普勒三定律
椭圆
1. 开普勒第一定律:所有的行星围绕太阳运动的轨道都是
________,太阳处在所有椭圆的一个焦点上.
2.开普勒第二定律:行星与太阳的连线在相同的时间内_____
________相等.
的面积
公转周期的二次方
3. 开普勒第三定律:所有行星的轨道的半长轴的三次方与
____________________的比值都相等.
扫过
r2
二、万有引力定律
质量的乘积
1.内容:自然界中任何两个物体都是互相吸引的,引力的大小
跟这两个物体的_____________成正比,跟它们的距离的二次方成
反比.
6.67×10-11 N·m2/kg2
质点
2.公式:F=G
m1m2
,其中 G=__________________,叫引力
常量,由英国物理学家卡文迪什利用扭秤装置第一次测得.
3.适用条件:公式适用于________间的相互作用.均匀的球体
也可视为质量集中于球心的质点,r 是两球心间的距离.
宇宙速度 数值(km/s) 意义
第一宇宙速度
(环绕速度) ①________ 是人造地球卫星的最②____发射速度,也是人造地球卫星绕地球做圆周运动的最③____速度
第二宇宙速度 ④________ 使物体挣脱⑤____引力束缚的最小发射速度
第三宇宙速度 ⑥________ 使物体挣脱⑦____引力束缚的最小发射速度
三、三种宇宙速度
7.9
小
大
11.2
地球
16.7
太阳
四、同步卫星
静止
24 h
1.概念:相对地面________的卫星称为同步卫星.
2.基本特征:①周期为地球自转周期 T=________;②轨道在
赤道平面内;③运动的角速度与地球的自转角速度相同;④高度 h
一定;⑤轨道和地球赤道为共面同心圆;⑥卫星运行速度一定.
【基础自测】
1.判断下列题目的正误.
(1)行星在椭圆轨道上运行速率是变化的,离太阳越远,运行
速率越大.(
)
(2)牛顿总结了前人的科研成果,在此基础上,经过研究得出
了万有引力定律.(
)
(3)牛顿利用扭秤实验装置比较准确地测出了引力常量.(
)
(4) 第一宇宙速度是卫星绕地球做匀速圆周运动的最小速
度.(
)
(5)若物体的速度大于第二宇宙速度而小于第三宇宙速度,则
物体可绕太阳运行.(
)
答案:(1)× (2)√ (3)× (4)× (5)√
2.(多选)如图所示,一颗卫星绕地球做椭圆运动,运动周期
为 T,图中虚线为卫星的运动轨迹,A、B、C、D 是轨迹上的四
个位置,其中 A 距离地球最近,C 距离地球最远.B 点和 D 点是
)
弧线 ABC 和 ADC 的中点,下列说法正确的是(
A.卫星在 A 点的速度最大
B.卫星在 C 点的加速度最大
答案:AC
3.(2022 年河北卷)2008 年,我国天文学家利用国家天文台兴
隆观测基地的 2.16 米望远镜,发现了一颗绕恒星 HD173416 运动
的系外行星 HD173416b,2019 年,该恒星和行星被国际天文学联
合会分别命名为“羲和”和“望舒”,天文观测得到恒星“羲
和”的质量是太阳质量的 2 倍,若将“望舒”与地球的公转均视
为匀速圆周运动,且公转的轨道半径相等.则望舒与地球公转速度
大小的比值为(
)
解析:地球绕太阳公转和行星“望舒”绕恒星“羲和”的匀
答案:C
4.(2024 年贵州卷)土星的部分卫星绕土星的运动可视为匀速
圆周运动,其中的两颗卫星轨道半径分别为r1、r2 且 r1≠r2,向
心加速度大小分别为 a1、a2,则(
)
答案:D
热点 1 万有引力与重力的关系
考向 1 考虑星球自转时,星球表面万有引力与重力的关系
[热点归纳]
地球对物体的万有引力 F 表现为两个效果:一是重力 mg,
二是提供物体随地球自转的向心力 F向,如图所示.
【典题 1】(2022 年广东广州模拟)现实版的倒霉熊乔伊曾因为
白化病两次被送到北极,还有一次被送到位于赤道的北极馆.若乔
伊质量始终为 m,它在北极和北极馆的重力差为ΔN,地球半径 R,
则可求出同步卫星运动的周期为(
)
答案:B
考向 2 不考虑星球自转时,星球表面万有引力与重力的关系
[热点归纳]
因为一般星球自转表面需要的向心力远小于重力,所以不研
【典题 2】质量为 m 的着陆器在着陆火星前,会在火星表面
附近经历一个时长为 t0、速度由 v0 减速到零的过程.已知火星的质
量约为地球的 0.1 倍,半径约为地球的 0.5 倍,地球表面的重力加
速度大小为 g,忽略火星大气阻力.若该减速过程可视为一个竖直
向下的匀减速直线运动,此过程中着陆器受到的制动力大小约为
(
)
答案:B
考向 3 天体表面某深度处的重力加速度
①推论 1:在匀质球壳的空腔内任意位置处,质点受到球壳的
万有引力的合力为零,即∑F引=0.
②推论 2:在匀质球体内部距离球心 r 处的质点(m)受到的万
有引力等于球体内半径为 r 的同心球体(M′)对其的万有引力,即
【典题 3】(2023 年海南海口三模)已知某星球的半径为 R,该
星球表面处的重力加速度大小为 g,不考虑星球的自转,则距离星
球表面高度为 3R 处的重力加速度大小为(
)
1
A. g
3
1
B. g
4
1
C. g
9
1
D. g
16
答案:D
热点 2 中心天体质量和密度的计算
[热点归纳]
天体质量和密度常用的估算方法.
(续表)
【典题4】(2024 年河南卷)天文学家发现,在太阳系外的一颗
红矮星有两颗行星绕其运行,其中行星 GJ1002c 的轨道近似为圆,
轨道半径约为日地距离的 0.07 倍,周期约为 0.06 年,则这颗红矮
)
星的质量约为太阳质量的(
A.0.001 倍
C.10 倍
B.0.1 倍
D.1000 倍
答案:B
方法技巧 估算天体质量和密度的四点注意
(1)利用万有引力提供天体圆周运动的向心力估算天体质量
时,估算的只是中心天体的质量,而非环绕天体的质量.
(2)区别天体半径 R 和卫星轨道半径 r,只有在天体表面附近
中心天体的半径.
(3)天体质量估算中常有隐含条件,如地球的自转周期为 24 h,
公转周期为 365 天等.
(4)注意黄金代换式 GM=gR2 的应用.
热点 3 卫星
[热点归纳]
地球卫星的运行参数.
(续表)
【典题 5】(2022 年广东卷)“祝融号”火星车需要“休眠”以
度过火星寒冷的冬季.假设火星和地球的冬季是各自公转周期的四
分之一,且火星的冬季时长约为地球的 1.88 倍.火星和地球绕太阳
的公转均可视为匀速圆周运动.下列关于火星、地球公转的说法正
确的是(
)
A.火星公转的线速度比地球的大
B.火星公转的角速度比地球的大
C.火星公转的半径比地球的小
D.火星公转的加速度比地球的小
答案:D
热点 4 宇宙速度
[热点归纳]
1.第一宇宙速度的推导
2.宇宙速度与运动轨迹的关系
(1)v发=7.9 km/s 时,卫星绕地球做匀速圆周运动.
(2)7.9 km/s<v发<11.2 km/s,卫星绕地球运动的轨迹为椭圆.
(3)11.2 km/s<v发<16.7 km/s,卫星绕太阳做椭圆运动.
(4)v发≥16.7 km/s,卫星将挣脱太阳引力的束缚,飞到太阳系
以外的空间.
【典题6】(多选,2024 年湖南卷)2024 年 5 月 3 日,“嫦娥
六号”探测器顺利进入地月转移轨道,正式开启月球之旅.相较于
“嫦娥四号”和“嫦娥五号”,本次的主要任务是登陆月球背面
进行月壤采集并通过升空器将月壤转移至绕月运行的返回舱,返
回舱再通过返回轨道返回地球.设返回舱绕月运行的轨道为圆轨
道,半径近似为月球半径.已知月球表面重力加速度约为地球表面
动,下列说法正确的是(
)
A.其相对于月球的速度大于地球第一宇宙速度
B.其相对于月球的速度小于地球第一宇宙速度
答案:BD
情景图 “双星”模型 “三星”模型 “四星”模型
“双星”和“三星”模型分析
“双星”“三星”和“四星”模型.
运动
特点 转动方向、周期、角速度相同,运动半径一般不等 转动方向、周期、角速度、线速度大小均相同,圆周运动半径相等 转动方向、周期、角速度、线速度大小均相同,圆周运动半径相等
受力
特点 两星间的万有引力提供两星圆周运动的向心力 各星所受万有引力的合力提供圆周运动的向心力 各星所受万有引力的合力提供圆周运动的向心力
(续表)
(续表)
【典题 7】(多选,2023 年海南海口一模)冥王星与其附近的另
一星体“卡戎”可视为双星系统,质量之比约为 7∶1,同时绕它
们连线上某点 O 做匀速圆周运动.由此可知(
)
A.冥王星的轨道半径约为“卡戎”的
1
7
B.冥王星的向心加速度大小约为“卡戎”的 7 倍
D.冥王星的动能约为“卡戎”的 7 倍
解析:冥王星 M 与“卡戎”m 组成双星系统,所以冥王星和
“卡戎”周期是相等的,角速度也是相等的.它们之间的万有引力
提供各自的向心力,则有 Mr1ω2=mr2ω2,解得 r1∶r2=m∶M=
1∶7,A 正确;根据向心加速度公式 an=ω2r 可知,两者的向心加
速度之比 an1∶an2=r1∶r2 =1∶7,B 错误;根据线速度 v=ωr 可得,
两者的线速度大小之比 v1∶v2=r1∶r2 =1∶7,C 正确;由万有引力
r1∶r2=1∶7,D 错误.
答案:AC
【触类旁通】(2022 年广东模拟)三颗质量相等的恒星彼此连
线恰好构成等边三角形,忽略其他星体对其引力,测量星体之间
距离,并通过理论计算得到该三星系统的周期为 T,但实际观测中
得到该三星系统周期为 nT,科学家猜测在三星构成的等边三角形
的中心存在质量为 M 的黑洞,该黑洞质量是恒星质量的(
)
答案:D
同课章节目录
