2025秋高考物理复习第四章第2节抛体运动课件
文档属性
| 名称 | 2025秋高考物理复习第四章第2节抛体运动课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-05 17:38:17 | ||
图片预览










文档简介
(共59张PPT)
第2节
抛体运动
一、平抛运动及其规律
1.平抛运动.
重力
(1)定义:水平方向抛出的物体只在________作用下运动.
(2)性质:平抛运动是加速度为 g 的匀加速曲线运动,其运动
轨迹是________.
抛物线
重力
(3)平抛运动的条件:①v0≠0,沿水平方向;②只受________
作用.
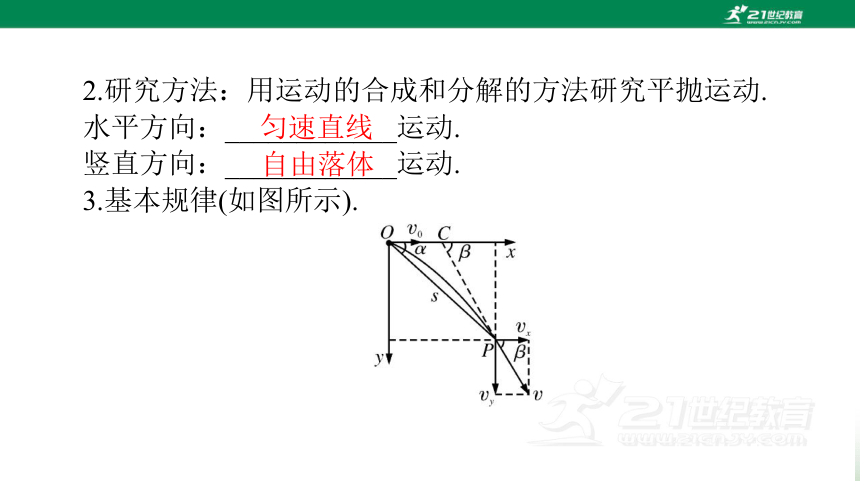
2.研究方法:用运动的合成和分解的方法研究平抛运动.
匀速直线
自由落体
水平方向:____________运动.
竖直方向:____________运动.
3.基本规律(如图所示).
(1)速度关系.
(2)位移关系.
注:综合(1)(2)可知 tan β=2tan α.
(3)轨迹方程:y=________.
gt
v0t
二、斜抛运动
1.定义:将物体以速度 v0 斜向上方或斜向下方抛出,物体只
在________作用下的运动.
重力
匀速直线
2.研究方法:斜抛运动可以看作是水平方向的_________运动
和竖直方向的竖直上抛运动的合运动.
3.基本规律(以斜向上抛为例说明,如图所示).
(1)水平方向:v0x=________,x=________.
(2)竖直方向:v0y =________,y=____________.
v0cos θ
v0cos θt
v0sin θ
【基础自测】
1.判断下列题目的正误.
(1)做平抛运动的物体的速度方向时刻在变化,加速度方向也
时刻在变化.(
)
(2)做平抛运动的物体初速度越大,水平位移越大.(
)
(3)做平抛运动的物体,初速度越大,在空中飞行时间越长.
(
)
(4)无论平抛运动还是斜抛运动,都是匀变速曲线运动.(
)
(5)做平抛运动的物体,在任意相等的时间内速度的变化量是
相同的.(
)
答案:(1)× (2)× (3)× (4)√ (5)√
2.质点从同一高度水平抛出,不计空气阻力,下列说法正确的
是(
)
A.质量越大,水平位移越大
B.初速度越大,落地时竖直方向速度越大
C.初速度越大,空中运动时间越长
D.初速度越大,落地速度越大
答案:D
3.(2024 年湖北卷)如图所示,有五片荷叶伸出荷塘水面,一只
青蛙要从高处荷叶跳到低处荷叶上.设低处荷叶 a、b、c、d 和青蛙
在同一竖直平面内,a、b 高度相同,c、d 高度相同,a、b 分别在
c、d 正上方.将青蛙的跳跃视为平抛运动,若以最小的初速度完成
跳跃,则它应跳到(
)
A.荷叶 a
B.荷叶 b
C.荷叶 c
D.荷叶 d
解析:青蛙做平抛运动,水平方向匀速直线,竖直方向自由
直高度越大,初速度越小,因此跳到荷叶 c 上面,C 正确.
答案:C
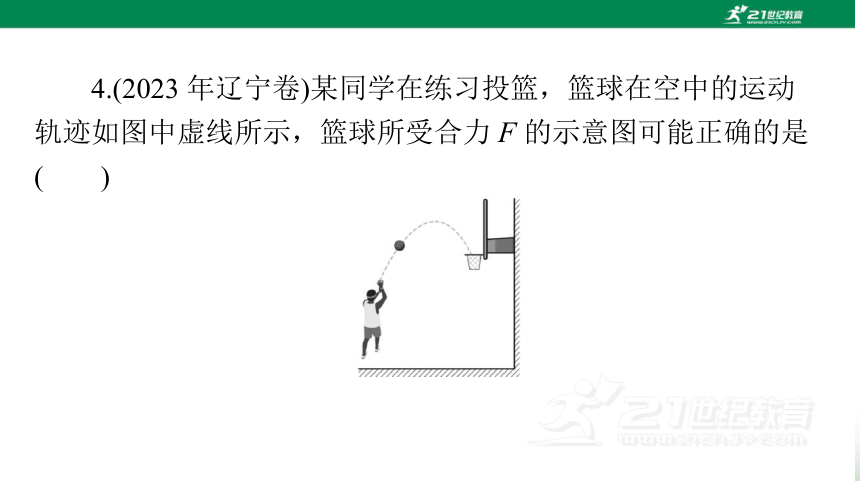
4.(2023 年辽宁卷)某同学在练习投篮,篮球在空中的运动
轨迹如图中虚线所示,篮球所受合力 F 的示意图可能正确的是
(
)
A
B
C
D
解析:篮球做曲线运动,所受合力指向运动轨迹的凹侧,
A正确.
答案:A
热点 1 平抛运动
[热点归纳]
关于平抛运动必须掌握的四个物理量.
(续表)
考向 1 对平抛运动的理解
【典题 1】(2023 年山东梁山一中期中)质点从同一高度水平抛
出,不计空气阻力,下列说法正确的是(
)
A.水平位移只与初速度有关
B.水平位移既跟高度有关,又跟初速度有关
C.初速度越大,运动时间越长
D.运动时间既跟高度有关,又跟初速度有关
运动时间越长,CD 错误;平抛运动竖直方向做匀速直线运动,有
A 错误,B 正确.
答案:B
考向 2 平抛运动的规律及应用
【典题 2】(多选,2022 年山东卷)如图所示,某同学将离
地 1.25 m 的网球以 13 m/s 的速度斜向上击出,击球点到竖直墙
壁的距离为 4.8 m.当网球竖直分速度为零时,击中墙壁上离地高度
为 8.45 m 的 P 点.网球与墙壁碰撞后,垂直墙面速度分量大小变为
碰前的 0.75 倍.平行墙面的速度分量不变.重力加速度 g 取 10 m/s2,
网球碰墙后的速度大小 v 和着地点到墙壁的距离 d 分别为(
)
A.v=5 m/s
B.v=
m/s
C.d=3.6 m
D.d=3.9 m
=3.9 m,BD 正确,AC 错误.
答案:BD
思路导引
这是一个三维空间的运动,与二维平面内物体的
运动分解思路一致,将运动分解为垂直墙向里的运动、平行于墙
向左的运动、平行于墙向上的运动,结合合运动与分运动的等时
性分别研究三个方向的运动.
【迁移拓展1】(2024 年湖南永州一模)2024 年 8 月 3 日,中
国选手在巴黎奥运会网球女单决赛中战胜克罗地亚选手夺冠,为
中国网球赢得史上首枚女单奥运金牌.如图所示,网球比赛中,运
动员甲某次在 B 点直线救球倒地后,运动员乙将球从距水平地面
上 D 点高度为 h 的 A 点水平击出,落点为 C.乙击球瞬间,甲同时
沿直线 BC 奔跑,恰好在球落地时赶到 C 点.已知 BC⊥BD,BD=
d,BC=l,网球和运动员甲均可视为质点,忽略空气阻力,则甲
此次奔跑的平均加速度大小与当地重力加速度大小之比为(
)
解析:设甲此次奔跑的平均加速度大小为 a,当地重力加速度
正确.
答案:A
热点 2 落点在斜面上的平抛运动
[热点归纳]
1.常见的几种模型.
(续表)
(续表)
2v0tan θ
2.抛出点和落点均在斜面上的平抛运动的特点.
(1)位移方向相同,竖直位移与水平位移之比等于斜面倾斜角
的正切值.
(2)末速度方向平行,竖直分速度与水平分速度(初速度)之比等
于斜面倾斜角正切值的 2 倍.
(3)运动的时间与初速度成正比:t=
g
.
(5)当速度与斜面平行时,物体到斜面的距离最远,且从抛出
到距斜面最远所用的时间为平抛运动时间的一半.
【典题3】(2022 年广东卷)如图所示是滑雪道的示意图.可视为
质点的运动员从斜坡上的 M 点由静止自由滑下,经过水平 NP 段
后飞入空中,在 Q 点落地.不计运动员经过 N 点的机械能损失,不
计摩擦力和空气阻力.下列能表示该过程运动员速度大小 v 或加速
度大小 a 随时间 t 变化的图像是(
)
A
C
B
D
解析:设斜坡倾角为θ,运动员在斜坡 MN 段做匀加速直线运
动,根据牛顿第二定律 mgsin θ=ma1,可得 a1=gsin θ,运动员在
水平 NP 段做匀速直线运动,加速度 a2=0,运动员从 P 点飞出后
做平抛运动,加速度为重力加速度 a3=g,设在 P 点的速度为 v0,
从P 点飞出后速度大小与时间的图像不可能为直线,且 a1<a3,
C 正确.
答案:C
【迁移拓展2】(2024 年广东深圳二模)如图所示,阳光垂直照
射到倾角为θ的斜面草坪上,在斜面草坪顶端把一高尔夫球以 v0
的速度水平击出,小球刚好落在斜面底端.B 点是球距离斜面的最
远处,草坪上 A 点是在阳光照射下球经过 B 点时的投影点,草坪
上 D 点在 B 点的正下方.不计空气阻力,则(
)
C.OA 与 AC 长度之比为 1∶3
D.OD 与 DC 长度之比为 1∶3
解析:将小球的运动分解为沿斜面和垂直斜面两个分运动,
可知小球垂直斜面方向做初速度为 v0sin θ,加速度为 gcos θ的匀减
速直线运动,B 点是运动过程中距离斜面的最远处,则此时小球
可知小球从 B 点运动到 C 点的时间等于从 O 点到 B 点运动的时间,
C 错误;将小球的运动分解为水平方
向的匀速运动和竖直方向的自由落体运动,如图所示.
则从O到B有xOB=v0t1,小球从O到C有xOC=v0·2t1=2xOB,
根据几何关系,可知 D 点是 OC 的中点,则 OD 与 DC 长度相等,
即 OD 与 DC 长度之比为 1∶1,D 错误.
答案:A
图示 规律
热点 3 落点在曲面上的平抛运动
[热点归纳]
1.常见的几种模型.
图示 规律
(续表)
2.平抛运动的两个重要推论.
(1)做平抛运动的物体在任意时刻的瞬时速度的反向延长线一
(2)做平抛(或类平抛)运动的物体在任一时刻,设其速度方向与
水平方向的夹角为θ,位移与水平方向的夹角为α,则 tan θ=2tan α.
如图所示.
【典题 4】(2022 年广东模拟)如图,在竖直平面内有一半
圆形轨道,圆心为 O,AB 为水平直径,D 点为半圆形轨道的最
低点,C 为轨道上的一点,CO 与水平直径的
夹角为 53°,甲、乙两小球分别从 B 点和 C
点水平抛出,两球都落到 D 点.不计空气阻力,
小球可视为质点,sin 53°=0.8,则甲、乙两
球初速度之比为(
)
解析:依题意,设圆形轨道半径为 R,对于甲球,水平方向
答案:B
思路导引 这是两个独立的平抛运动,根据几何关系确定各自
的水平位移和竖直位移,分别在水平方向和竖直方向列方程求解.
热点 4 斜抛运动
[热点归纳]
1.斜抛运动的速度公式(θ为初位置速度与水平方向夹角).
2.斜抛运动的位置坐标.
3.对称性特点.
(1)速度对称:相对于轨道最高点两侧对称
的两点速度大小相等,或水平方向速度相等、
竖直方向速度等大反向(如图).
(2)时间对称:相对于轨道最高点两侧对称
的曲线上升时间等于下降时间.
(3)轨迹对称:其运动轨迹关于过最高点的竖直线对称.
【典题5】(2024 年广东深圳月考)图甲是北京冬奥会单板滑雪
大跳台比赛项目中运动员在空中姿态的合成图.比赛场地分为助滑
区、起跳台、着陆坡和终点区域四个部分.运动员进入起跳台后的
运动可简化成如图乙所示,先以水平初速度 v0 从 A 点冲上圆心角
为α的圆弧跳台,从 B 点离开跳台,C 点为运动轨迹最高点,之后
落在着陆坡上的 E 点.忽略运动过程中受到的空气阻力并将运动员
及装备看成质点,则下列说法正确的是(
)
甲
乙
A.运动员在 C 点速度为 0
B.运动员在 AB 圆弧轨道上运动时处于失重状态
C.运动员从 B 到 C 与从 C 到 E 两个过程的速度变化量方向相反
D.运动员以更大的初速度从 A 点冲上轨道,运动轨迹的最高
点在 C 点的右上方
解析:运动员在 C 点时具有水平速度,即速度不为 0,A 错
误;运动员在 AB 圆弧轨道上运动时设速度与水平方向夹角为θ,
则其竖直方向分速度为 v竖直=vsin θ运动员从 A 运动到 B 过程,
其线速度减小,θ增大,导致 sin θ增大,可知 v 竖直先增大后减小,
即运动员竖直方向加速度先竖直向上后竖直向下,运动员先处于
超重状态后出于失重状态,B 错误;由Δv=gt 可知运动员从 B 到
C 与从 C 到 E 两个过程的速度变化量方向均竖直向下,方向相同,
C 错误;运动员以更大的初速度从 A 点冲上轨道,则从 B 点离开
分位移和竖直分位移均增大,运动轨迹的最高点在 C 点的右上方,
D 正确.
答案:D
热点 5 实验探究平抛运动的特点
【典题6】(2024 年广东汕头二模)乔乔同学用平抛运动规律来
测量木制小球从玩具轨道顶部滚落到水平底部时的速度.装置图如
图甲所示,需要用到的器材有:新买的学习桌、配送的气泡水平
仪、包装用的快递盒(瓦楞纸板)和刻度尺.实验步骤如下:
甲
乙
(1)将桌子边缘与地板纹路平行,轨道底部与桌子边缘对齐.
(2)利用气泡水平仪将桌面调至水平.通过查阅说明书,乔乔知
道气泡在水平仪中总保持在最高位置,当气泡处于参考线内时,
安装面达到水平.将水平仪贴近桌子边缘,俯视图如图乙,右侧气
泡不在参考线内,此时应该将__________(填“1 号”“2 号”“3
号”或“4 号”)两个桌脚适当垫高.
(3)把瓦楞纸板固定在架子上,调节好架子让瓦楞纸板正对轨
道固定在水平地面上;将小球沾上墨水,并记录小球在轨道开始
下滑的位置为 O 点,静止释放小球,小球飞出后在瓦楞纸板留下
痕迹.
(4)将瓦楞纸板往远离桌子方向平行移动距离 D,并固定,
____________________(填写操作步骤).重复此步骤 4 次,瓦楞纸
板留下点迹如图.
(5)用刻度尺测量 AB、BC、CD 之间的距离 y1=16.87 cm、
y2=28.97 cm、y3=41.07 cm,重力加速度 g 取 10 m/s2,则相邻两
次实验小球在空中运动的时间之差为 T=________(结果保留 2 位
有效数字).
(6)用刻度尺测量瓦楞纸板每次平行移动的距离 D=12.0 cm,
则小球从轨道底部水平飞出的速度 v0=__________m/s(结果保留
3 位有效数字).
(7)完成实验后,乔乔对实验进行评价反思,可能引起误差的
原因有________(填字母).
A.未测量水平轨道底部离桌面高度
B.瓦楞纸板厚度不可忽略
C.小球下落过程中有空气阻力
D.通过小球在瓦楞纸板上的痕迹,通过圆心确定位置时存在
误差
解析:(2)由图乙可知气泡偏右,说明桌子左侧低,应该将1号、
4号桌脚适当垫高.(4)实验中应保持平抛运动的初速度不变,需要小
球从 O 点由静止开始下滑.(5)相邻两次实验小球在空中运动的时
间之差为y2-y1=gT2,解得T=0.11 s.(6)小球从轨道底部水平飞出
部离桌面高度,不影响小球竖直位移,A 错误;瓦楞纸板厚度不
影响水平位移,可忽略,B 错误;小球下落过程中有空气阻力,
影响水平位移和竖直位移,C 正确;通过小球在瓦楞纸板上的痕
迹,通过圆心确定位置时存在误差,影响竖直位移,D 正确.
答案:(2)1 号、4 号
(4)小球从 O 点由静止开始下滑
(5)0.11 s
(6)1.09
(7)CD
第2节
抛体运动
一、平抛运动及其规律
1.平抛运动.
重力
(1)定义:水平方向抛出的物体只在________作用下运动.
(2)性质:平抛运动是加速度为 g 的匀加速曲线运动,其运动
轨迹是________.
抛物线
重力
(3)平抛运动的条件:①v0≠0,沿水平方向;②只受________
作用.
2.研究方法:用运动的合成和分解的方法研究平抛运动.
匀速直线
自由落体
水平方向:____________运动.
竖直方向:____________运动.
3.基本规律(如图所示).
(1)速度关系.
(2)位移关系.
注:综合(1)(2)可知 tan β=2tan α.
(3)轨迹方程:y=________.
gt
v0t
二、斜抛运动
1.定义:将物体以速度 v0 斜向上方或斜向下方抛出,物体只
在________作用下的运动.
重力
匀速直线
2.研究方法:斜抛运动可以看作是水平方向的_________运动
和竖直方向的竖直上抛运动的合运动.
3.基本规律(以斜向上抛为例说明,如图所示).
(1)水平方向:v0x=________,x=________.
(2)竖直方向:v0y =________,y=____________.
v0cos θ
v0cos θt
v0sin θ
【基础自测】
1.判断下列题目的正误.
(1)做平抛运动的物体的速度方向时刻在变化,加速度方向也
时刻在变化.(
)
(2)做平抛运动的物体初速度越大,水平位移越大.(
)
(3)做平抛运动的物体,初速度越大,在空中飞行时间越长.
(
)
(4)无论平抛运动还是斜抛运动,都是匀变速曲线运动.(
)
(5)做平抛运动的物体,在任意相等的时间内速度的变化量是
相同的.(
)
答案:(1)× (2)× (3)× (4)√ (5)√
2.质点从同一高度水平抛出,不计空气阻力,下列说法正确的
是(
)
A.质量越大,水平位移越大
B.初速度越大,落地时竖直方向速度越大
C.初速度越大,空中运动时间越长
D.初速度越大,落地速度越大
答案:D
3.(2024 年湖北卷)如图所示,有五片荷叶伸出荷塘水面,一只
青蛙要从高处荷叶跳到低处荷叶上.设低处荷叶 a、b、c、d 和青蛙
在同一竖直平面内,a、b 高度相同,c、d 高度相同,a、b 分别在
c、d 正上方.将青蛙的跳跃视为平抛运动,若以最小的初速度完成
跳跃,则它应跳到(
)
A.荷叶 a
B.荷叶 b
C.荷叶 c
D.荷叶 d
解析:青蛙做平抛运动,水平方向匀速直线,竖直方向自由
直高度越大,初速度越小,因此跳到荷叶 c 上面,C 正确.
答案:C
4.(2023 年辽宁卷)某同学在练习投篮,篮球在空中的运动
轨迹如图中虚线所示,篮球所受合力 F 的示意图可能正确的是
(
)
A
B
C
D
解析:篮球做曲线运动,所受合力指向运动轨迹的凹侧,
A正确.
答案:A
热点 1 平抛运动
[热点归纳]
关于平抛运动必须掌握的四个物理量.
(续表)
考向 1 对平抛运动的理解
【典题 1】(2023 年山东梁山一中期中)质点从同一高度水平抛
出,不计空气阻力,下列说法正确的是(
)
A.水平位移只与初速度有关
B.水平位移既跟高度有关,又跟初速度有关
C.初速度越大,运动时间越长
D.运动时间既跟高度有关,又跟初速度有关
运动时间越长,CD 错误;平抛运动竖直方向做匀速直线运动,有
A 错误,B 正确.
答案:B
考向 2 平抛运动的规律及应用
【典题 2】(多选,2022 年山东卷)如图所示,某同学将离
地 1.25 m 的网球以 13 m/s 的速度斜向上击出,击球点到竖直墙
壁的距离为 4.8 m.当网球竖直分速度为零时,击中墙壁上离地高度
为 8.45 m 的 P 点.网球与墙壁碰撞后,垂直墙面速度分量大小变为
碰前的 0.75 倍.平行墙面的速度分量不变.重力加速度 g 取 10 m/s2,
网球碰墙后的速度大小 v 和着地点到墙壁的距离 d 分别为(
)
A.v=5 m/s
B.v=
m/s
C.d=3.6 m
D.d=3.9 m
=3.9 m,BD 正确,AC 错误.
答案:BD
思路导引
这是一个三维空间的运动,与二维平面内物体的
运动分解思路一致,将运动分解为垂直墙向里的运动、平行于墙
向左的运动、平行于墙向上的运动,结合合运动与分运动的等时
性分别研究三个方向的运动.
【迁移拓展1】(2024 年湖南永州一模)2024 年 8 月 3 日,中
国选手在巴黎奥运会网球女单决赛中战胜克罗地亚选手夺冠,为
中国网球赢得史上首枚女单奥运金牌.如图所示,网球比赛中,运
动员甲某次在 B 点直线救球倒地后,运动员乙将球从距水平地面
上 D 点高度为 h 的 A 点水平击出,落点为 C.乙击球瞬间,甲同时
沿直线 BC 奔跑,恰好在球落地时赶到 C 点.已知 BC⊥BD,BD=
d,BC=l,网球和运动员甲均可视为质点,忽略空气阻力,则甲
此次奔跑的平均加速度大小与当地重力加速度大小之比为(
)
解析:设甲此次奔跑的平均加速度大小为 a,当地重力加速度
正确.
答案:A
热点 2 落点在斜面上的平抛运动
[热点归纳]
1.常见的几种模型.
(续表)
(续表)
2v0tan θ
2.抛出点和落点均在斜面上的平抛运动的特点.
(1)位移方向相同,竖直位移与水平位移之比等于斜面倾斜角
的正切值.
(2)末速度方向平行,竖直分速度与水平分速度(初速度)之比等
于斜面倾斜角正切值的 2 倍.
(3)运动的时间与初速度成正比:t=
g
.
(5)当速度与斜面平行时,物体到斜面的距离最远,且从抛出
到距斜面最远所用的时间为平抛运动时间的一半.
【典题3】(2022 年广东卷)如图所示是滑雪道的示意图.可视为
质点的运动员从斜坡上的 M 点由静止自由滑下,经过水平 NP 段
后飞入空中,在 Q 点落地.不计运动员经过 N 点的机械能损失,不
计摩擦力和空气阻力.下列能表示该过程运动员速度大小 v 或加速
度大小 a 随时间 t 变化的图像是(
)
A
C
B
D
解析:设斜坡倾角为θ,运动员在斜坡 MN 段做匀加速直线运
动,根据牛顿第二定律 mgsin θ=ma1,可得 a1=gsin θ,运动员在
水平 NP 段做匀速直线运动,加速度 a2=0,运动员从 P 点飞出后
做平抛运动,加速度为重力加速度 a3=g,设在 P 点的速度为 v0,
从P 点飞出后速度大小与时间的图像不可能为直线,且 a1<a3,
C 正确.
答案:C
【迁移拓展2】(2024 年广东深圳二模)如图所示,阳光垂直照
射到倾角为θ的斜面草坪上,在斜面草坪顶端把一高尔夫球以 v0
的速度水平击出,小球刚好落在斜面底端.B 点是球距离斜面的最
远处,草坪上 A 点是在阳光照射下球经过 B 点时的投影点,草坪
上 D 点在 B 点的正下方.不计空气阻力,则(
)
C.OA 与 AC 长度之比为 1∶3
D.OD 与 DC 长度之比为 1∶3
解析:将小球的运动分解为沿斜面和垂直斜面两个分运动,
可知小球垂直斜面方向做初速度为 v0sin θ,加速度为 gcos θ的匀减
速直线运动,B 点是运动过程中距离斜面的最远处,则此时小球
可知小球从 B 点运动到 C 点的时间等于从 O 点到 B 点运动的时间,
C 错误;将小球的运动分解为水平方
向的匀速运动和竖直方向的自由落体运动,如图所示.
则从O到B有xOB=v0t1,小球从O到C有xOC=v0·2t1=2xOB,
根据几何关系,可知 D 点是 OC 的中点,则 OD 与 DC 长度相等,
即 OD 与 DC 长度之比为 1∶1,D 错误.
答案:A
图示 规律
热点 3 落点在曲面上的平抛运动
[热点归纳]
1.常见的几种模型.
图示 规律
(续表)
2.平抛运动的两个重要推论.
(1)做平抛运动的物体在任意时刻的瞬时速度的反向延长线一
(2)做平抛(或类平抛)运动的物体在任一时刻,设其速度方向与
水平方向的夹角为θ,位移与水平方向的夹角为α,则 tan θ=2tan α.
如图所示.
【典题 4】(2022 年广东模拟)如图,在竖直平面内有一半
圆形轨道,圆心为 O,AB 为水平直径,D 点为半圆形轨道的最
低点,C 为轨道上的一点,CO 与水平直径的
夹角为 53°,甲、乙两小球分别从 B 点和 C
点水平抛出,两球都落到 D 点.不计空气阻力,
小球可视为质点,sin 53°=0.8,则甲、乙两
球初速度之比为(
)
解析:依题意,设圆形轨道半径为 R,对于甲球,水平方向
答案:B
思路导引 这是两个独立的平抛运动,根据几何关系确定各自
的水平位移和竖直位移,分别在水平方向和竖直方向列方程求解.
热点 4 斜抛运动
[热点归纳]
1.斜抛运动的速度公式(θ为初位置速度与水平方向夹角).
2.斜抛运动的位置坐标.
3.对称性特点.
(1)速度对称:相对于轨道最高点两侧对称
的两点速度大小相等,或水平方向速度相等、
竖直方向速度等大反向(如图).
(2)时间对称:相对于轨道最高点两侧对称
的曲线上升时间等于下降时间.
(3)轨迹对称:其运动轨迹关于过最高点的竖直线对称.
【典题5】(2024 年广东深圳月考)图甲是北京冬奥会单板滑雪
大跳台比赛项目中运动员在空中姿态的合成图.比赛场地分为助滑
区、起跳台、着陆坡和终点区域四个部分.运动员进入起跳台后的
运动可简化成如图乙所示,先以水平初速度 v0 从 A 点冲上圆心角
为α的圆弧跳台,从 B 点离开跳台,C 点为运动轨迹最高点,之后
落在着陆坡上的 E 点.忽略运动过程中受到的空气阻力并将运动员
及装备看成质点,则下列说法正确的是(
)
甲
乙
A.运动员在 C 点速度为 0
B.运动员在 AB 圆弧轨道上运动时处于失重状态
C.运动员从 B 到 C 与从 C 到 E 两个过程的速度变化量方向相反
D.运动员以更大的初速度从 A 点冲上轨道,运动轨迹的最高
点在 C 点的右上方
解析:运动员在 C 点时具有水平速度,即速度不为 0,A 错
误;运动员在 AB 圆弧轨道上运动时设速度与水平方向夹角为θ,
则其竖直方向分速度为 v竖直=vsin θ运动员从 A 运动到 B 过程,
其线速度减小,θ增大,导致 sin θ增大,可知 v 竖直先增大后减小,
即运动员竖直方向加速度先竖直向上后竖直向下,运动员先处于
超重状态后出于失重状态,B 错误;由Δv=gt 可知运动员从 B 到
C 与从 C 到 E 两个过程的速度变化量方向均竖直向下,方向相同,
C 错误;运动员以更大的初速度从 A 点冲上轨道,则从 B 点离开
分位移和竖直分位移均增大,运动轨迹的最高点在 C 点的右上方,
D 正确.
答案:D
热点 5 实验探究平抛运动的特点
【典题6】(2024 年广东汕头二模)乔乔同学用平抛运动规律来
测量木制小球从玩具轨道顶部滚落到水平底部时的速度.装置图如
图甲所示,需要用到的器材有:新买的学习桌、配送的气泡水平
仪、包装用的快递盒(瓦楞纸板)和刻度尺.实验步骤如下:
甲
乙
(1)将桌子边缘与地板纹路平行,轨道底部与桌子边缘对齐.
(2)利用气泡水平仪将桌面调至水平.通过查阅说明书,乔乔知
道气泡在水平仪中总保持在最高位置,当气泡处于参考线内时,
安装面达到水平.将水平仪贴近桌子边缘,俯视图如图乙,右侧气
泡不在参考线内,此时应该将__________(填“1 号”“2 号”“3
号”或“4 号”)两个桌脚适当垫高.
(3)把瓦楞纸板固定在架子上,调节好架子让瓦楞纸板正对轨
道固定在水平地面上;将小球沾上墨水,并记录小球在轨道开始
下滑的位置为 O 点,静止释放小球,小球飞出后在瓦楞纸板留下
痕迹.
(4)将瓦楞纸板往远离桌子方向平行移动距离 D,并固定,
____________________(填写操作步骤).重复此步骤 4 次,瓦楞纸
板留下点迹如图.
(5)用刻度尺测量 AB、BC、CD 之间的距离 y1=16.87 cm、
y2=28.97 cm、y3=41.07 cm,重力加速度 g 取 10 m/s2,则相邻两
次实验小球在空中运动的时间之差为 T=________(结果保留 2 位
有效数字).
(6)用刻度尺测量瓦楞纸板每次平行移动的距离 D=12.0 cm,
则小球从轨道底部水平飞出的速度 v0=__________m/s(结果保留
3 位有效数字).
(7)完成实验后,乔乔对实验进行评价反思,可能引起误差的
原因有________(填字母).
A.未测量水平轨道底部离桌面高度
B.瓦楞纸板厚度不可忽略
C.小球下落过程中有空气阻力
D.通过小球在瓦楞纸板上的痕迹,通过圆心确定位置时存在
误差
解析:(2)由图乙可知气泡偏右,说明桌子左侧低,应该将1号、
4号桌脚适当垫高.(4)实验中应保持平抛运动的初速度不变,需要小
球从 O 点由静止开始下滑.(5)相邻两次实验小球在空中运动的时
间之差为y2-y1=gT2,解得T=0.11 s.(6)小球从轨道底部水平飞出
部离桌面高度,不影响小球竖直位移,A 错误;瓦楞纸板厚度不
影响水平位移,可忽略,B 错误;小球下落过程中有空气阻力,
影响水平位移和竖直位移,C 正确;通过小球在瓦楞纸板上的痕
迹,通过圆心确定位置时存在误差,影响竖直位移,D 正确.
答案:(2)1 号、4 号
(4)小球从 O 点由静止开始下滑
(5)0.11 s
(6)1.09
(7)CD
同课章节目录
