2025秋高考物理复习第十四章第2节气体液体固体课件
文档属性
| 名称 | 2025秋高考物理复习第十四章第2节气体液体固体课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-05 17:38:17 | ||
图片预览











文档简介
(共78张PPT)
第2节
气体
液体
固体
一、气体的性质
平均动能
容积
1.气体的状态参量.
(1)温度:在宏观上表示物体的冷热程度;在微观上是分子
____________的标志.
(2)体积:气体总是充满它所在的容器,所以气体的体积总是
等于盛装气体的容器的________.
频繁碰撞
(3)压强:气体的压强是由于气体分子____________器壁而产
生的.
2.气体分子动理论.
(1)气体分子运动的特点.
大
它能达到的整个空间
①气体分子间距较______,分子力可以忽略,因此分子间除
碰撞外不受其他力的作用,故气体能充满_____________________.
②分子做无规则的运动,速率有大有小,且时而变化,大量
分子的速率按“__________,__________”的规律分布.
③温度升高时,速率小的分子数________,速率大的分子数
________,分子的平均速率将________,但速率分布规律不变.
中间多
两头少
减少
增多
增大
(2)气体压强的微观意义.
气体的压强是大量分子频繁碰撞器壁产生的.压强的大小跟两
个因素有关:①气体分子的________;②气体分子的_________.
平均动能
密集程度
项目 玻意耳定律 查理定律 盖-吕萨克定律
内容 一定质量的某种
气体,在温度不变
的情况下,压强与
体积成①_______ 一定质量的某种气
体,在体积不变的情
况下,压强与热力学
温度成②_____ 一定质量的某种
气体,在压强不变
的情况下,其体积
与热力学温度成
③________
3.气体实验定律.
反比
正比
正比
项目 玻意耳定律 查理定律 盖-吕萨克定律
表达式 ④__________ ⑤__________
或⑥________ ⑦__________
或⑧__________
图像
(续表)
p1V1=p2V2
4.理想气体的状态方程.
pV
T
一定质量的理想气体的状态方程:_______=C(恒量).
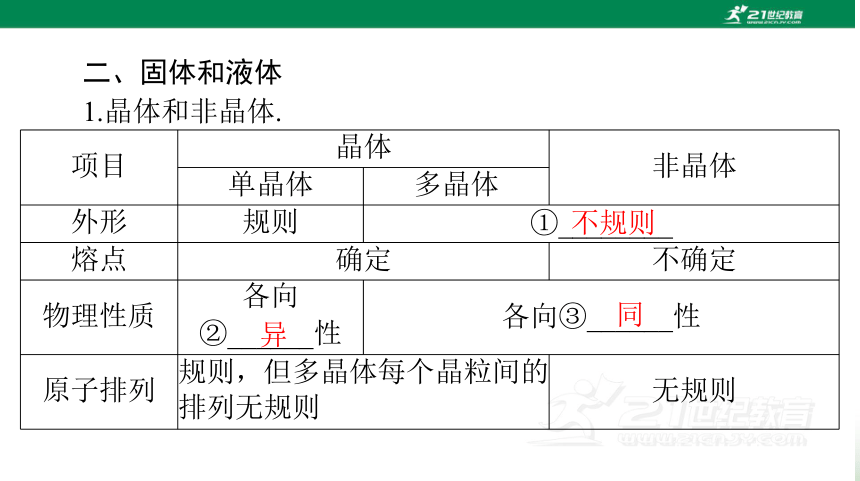
项目 晶体 非晶体
单晶体 多晶体
外形 规则 ①________
熔点 确定 不确定
物理性质 各向
②______性 各向③______性
原子排列 规则,但多晶体每个晶粒间的
排列无规则 无规则
二、固体和液体
1.晶体和非晶体.
不规则
异
同
项目 晶体 非晶体
单晶体 多晶体
形成与
转化 有的物质在不同条件下能够形成不同的④________;
同一物质可能以⑤__________ 和⑥________ 两种不
同的形态出现;有些⑦______在一定的条件下也可转
化为⑧________
典型物质 石英、云母、食盐、硫酸铜 玻璃、蜂蜡、松香
(续表)
晶体
晶体
非晶体
晶体
非晶体
注意:多晶体没有确定的几何形状,且多晶体是各向同性的.
2.液体、液晶.
吸引
(1)液体的表面张力.
液体表面各部分间相互________的力叫表面张力.表面张力使
液体自动收缩,液体表面有收缩到最小的趋势.表面张力的方向和
液面相切;其大小除了跟边界线的长度有关外,还跟液体的种类、
温度有关.
(2)液晶的特性.
异
流动性
液体
①液晶分子既保持排列有序而显示各向______性,又可以自
由移动位置,保持了液体的____________.
②液晶分子的位置无序使它像_______,排列有序使它像晶体.
③液晶分子的排列从某个方向看比较整齐,从另一个方向看
则是杂乱无章的.
④液晶的物理性质很容易在外界的影响下发生改变.
【基础自测】
1.判断下列题目的正误.
(1)晶体有天然规则的几何形状,是因为晶体的物质微粒是规
则排列的.(
)
(2)单晶体的所有物理性质都是各向异性的.(
)
(3)多晶体和非晶体的物理性质都是各向同性的.(
)
(4)液晶是液体和晶体的混合物.(
)
(5)小船浮于水面上不是由于液体的表面张力.(
)
答案:(1)√ (2)× (3)√ (4)× (5)√
2.“嫦娥五号”探测器顺利完成月球采样任务并返回地球.
探测器上装有用石英制成的传感器,其受压时表面会产生大小
相等、符号相反的电荷——压电效应.如图所示,石英晶体沿垂
直于 x 轴晶面上的压电效应最显著.下列
)
关于石英晶体说法正确的是(
A.没有确定的熔点
B.具有各向同性的压电效应
C.没有确定的几何形状
D.是单晶体
答案:D
3.对一定质量的气体,若用 N 表示单位时间内与器壁单位面
积碰撞的分子数,则下列说法正确的是(
)
A.当体积减小时,N 必定增加
B.当温度升高时,N 必定增加
C.当压强不变而体积和温度变化时,N 必定变化
D.当体积不变而压强和温度变化时,N 可能不变
解析:气体的体积减小或温度升高时,压强和温度是怎样变
化的并不清楚,不能判断 N 是必定增加的,A、B 错误;当压强不
变而体积和温度变化时,存在两种变化的可能性:一是体积增大
时,温度升高,分子的平均动能变大,即分子对器壁碰撞的力度
增大,因压强不变,因此对器壁碰撞的频繁度降低,就是 N 减小.
二是体积减小时,温度降低,同理可推知 N 增大,C 正确,D 错
误.
答案:C
4.一定质量的气体在温度保持不变的情况下,压强增大到原来
的 4 倍,则气体的体积变为原来的(
)
A.4
B.2
C.
1
2
1
D.
4
答案:D
热点 1 固体与液体的性质
考向 1 固体的性质
[热点归纳]
晶体和非晶体.
(1)单晶体具有各向异性,但不是在各种物理性质上都表现出
各向异性.
(2)只要是具有各向异性的物体必定是晶体,且是单晶体.
(3)只要是具有确定熔点的物体必定是晶体,反之,必是非晶
体.
(4)晶体和非晶体在一定条件下可以相互转化.
【典题 1】(多选)玻璃的出现和使用在人类生活里已有四千多
)
年的历史,它是一种非晶体.下列关于玻璃的说法正确的有(
A.没有固定的熔点
B.天然具有规则的几何形状
C.沿不同方向的导热性能相同
D.分子在空间上周期性排列
解析:根据非晶体的特点可知,非晶体是指组成物质的分子(或
原子、离子)不呈空间有规则周期性排列的固体.它没有一定规则的
外形.它的物理性质在各个方向上是相同的,叫“各向同性”.它没
有固定的熔点, AC 正确.
答案:AC
形成原因 表面层中分子间的距离比液体内部分子间的距离大,
分子间的相互作用力表现为引力
表面特性 表面层分子间的引力使液面产生了表面张力,使液体
表面好像一层绷紧的弹性薄膜
考向 2 液体的性质
[热点归纳]
液体表面张力.
表面张力
的方向 和液面相切,垂直于液面上的各条分界线
表面张力
的效果 表面张力使液体表面具有收缩趋势,使液体表面积趋
于最小,而在体积相同的条件下,球形的表面积最小
(续表)
【典题 2】往两个玻璃杯中分别注入水和水银,液面出现如
图所示现象,下列说法正确的是( )
A.水不浸润玻璃
B.水银浸润玻璃
C.玻璃分子对附着层内水分子的吸引力大
于水内部分子之间的吸引力
D.玻璃分子对附着层内水银分子的吸引力
大于水银内部分子之间的吸引力
解析:水浸润玻璃,水银不浸润玻璃,浸润与否关键看附着
层的分子间距与液体分子间距比较,如果附着层中的分子密度大
( 即容器壁对液体分子的吸引力大于液
体分子对液体分子的吸引力),则表现为
附着层中的分子作用力表现为斥力,使
得液面张开,表现为浸润现象,反之相
同分析,可以如图所示理解.
答案:C
热点 2 气体压强的产生与计算
考向 1 压强的产生
[热点归纳]
1.产生的原因:气体的压强是大量分子频繁地碰撞器壁而产生
的,单个分子碰撞器壁的冲力是短暂的,但大量分子频繁地碰撞
器壁,对器壁就产生了持续、平均的作用力,数值上气体压强等
于大量分子作用在器壁单位面积的平均作用力.
2.决定因素:
(1)从宏观上看,气体压强由体积和温度决定.
(2)从微观上看,气体压强由气体分子的密集程度和平均动能
决定.
A.是由气体分子间的相互作用力(吸引和排斥)产生的
B.是由大量气体分子频繁地碰撞器壁所产生的
C.是由气体受到的重力所产生的
D.当容器自由下落时将减小为零
解析:气体压强产生的原因:大量做无规则热运动的分子对
器壁频繁、持续地碰撞产生了气体的压强,AC 错误,B 正确;
当容器自由下落时,虽然处于失重状态,但分子热运动不会停止,
故压强不会减小为零,D 错误.
答案:ACD
方法技巧
(1)气体压强与大气压强不同,大气压强由重力而
产生,随高度增大而减小,气体压强由大量气体分子频繁碰撞器
壁而产生,大小不随高度而变化.
(2)容器内气体的压强是大量分子频繁碰撞器壁而产生的,并
非因其重力而产生.
平衡
状态 力平
衡法 选取与气体接触的液柱(或活塞)为研究对象进行受力分析,得到液柱(或活塞)的受力平衡方程,求得气体的压强
等压
面法 在连通器中,同一种液体(中间不间断)同一深度处压强相等.液体内深h处的总压强 p=p0+ρgh,p0 为液面上方的压强
考向 2 压强的计算
[热点归纳]
1.封闭气体压强的求法.
平衡
状态 液片法 选取假想的液体薄片( 自身重力不计) 为研究对
象,分析液片两侧受力情况,建立平衡方程,消
去面积,得到液片两侧压强相等方程,求得气体
的压强
加速
运动
系统 选取与气体接触的液柱(或活塞)为研究对象,进行受力分
析,利用牛顿第二定律列方程求解.
(续表)
2.气体压强计算的两类模型.
(1)活塞模型.
如图所示是最常见的封闭气体的两种方式.
甲
乙
对“活塞模型”类求压强的问题,其基本的方法就是先对
“活塞”进行受力分析,然后根据平衡条件或牛顿第二定律列方
程.图甲中活塞的质量为 m,活塞横截面积为 S,外界大气压强为
p0.由于活塞处于平衡状态,所以 p0S+mg=pS.
(2)连通器模型.
如图 所示,“U”形管竖直放置.根据帕斯卡定律可知,同
一液体中的相同高度处压强一定相等.所以气体 B 和 A 的压强关
系可由图中虚线所示的等高线联系起来.则有 pB+ρgh2=pA.
而 pA=p0+ρgh1,
所以气体 B 的压强为
pB=p0+ρg(h1-h2).
其实该类问题与“活塞模型”并没有什么本质的区别.熟练后
以上压强的关系式均可直接写出,不一定都要从受力分析入手.
【典题 4】(2021年山东淄博段考)如图所示,一个横截面
积为 S 的圆筒形容器竖直放置,容器上端放一金属圆板,金属
圆板的上表面是水平的,下表面是倾斜的,下表面与
水平面的夹角为θ,圆板的质量为 M,不计圆板与容
器内壁的摩擦.若大气压强为p0,则被圆板封闭在容器
中的气体的压强为下列选项中的(
)
·cos θ=Mg+p0S
解析:圆板的下表面是倾斜的,气体对其产生的压力应与该
面垂直.为求气体的压强,应以封闭气体的金属圆板
为研究对象,其受力分析如图所示.
由物体的平衡条件得 p
S
cos θ
解得 p=p0+
Mg
.
S
答案:D
热点 3 气体实验定律和理想气体状态方程
[热点归纳]
1.理想气体.
(1)宏观上讲,理想气体是指在任何条件下始终遵守气体实验
定律的气体,实际中气体在压强不太大、温度不太低的条件下,
可视为理想气体.
(2)微观上讲,理想气体的分子间除碰撞外无其他作用力,分
子本身没有体积,即它所占据的空间认为都是可以被压缩的空间.
2.理想气体状态方程与气体实验定律的关系.
3.两个重要的推论.
考向 1 等温变化
【典题 5】(2023 年湖北卷)如图所示,竖直放置在水平桌面
上的左右两汽缸粗细均匀,内壁光滑,横截面积分别为S、2S,
由体积可忽略的细管在底部连通.两汽缸中各有一轻质活塞将一定
质量的理想气体封闭,左侧汽缸底部与活塞用轻质细弹簧相连.初
始时,两汽缸内封闭气柱的高度均为 H,弹簧长度恰好为原长.现
往右侧活塞上表面缓慢添加一定质量的沙子,直至右侧活塞下降
汽缸足够长,汽缸内气体温度始终不变,弹簧始终在弹性限度内.
求:
(1)最终汽缸内气体的压强.
(2)弹簧的劲度系数和添加的沙子质量.
解:(1)对左右气缸内所封的气体,初态压强为 p1=p0,体积
为
V1=SH+2SH=3SH
末态压强为 p2,体积为
(2)设添加的沙子质量为 m,对右边活塞受力分析可知
mg+p0·2S=p2·2S
对左侧活塞受力分析可知
考向 2 等容变化
【典题 6】(2023 年海南卷)如图所示,某饮
料瓶内密封一定质量的理想气体,t=27 ℃时,
压强 p=1.050×105 Pa,则
(1)t′=37 ℃时,气压是多大?
(2)保持温度不变,挤压气体,使之压强与(1)
相同时,气体体积变为原来的多少倍?
解:(1)瓶内气体的始末状态的热力学温度分别为
T=(27+273) K=300 K
T′=(37+273) K=310 K
解得 p′=1.085×105 Pa.
(2)保持温度不变,挤压气体,等温变化过程,由玻意耳定律
有 pV=p′V′
解得 V′≈0.97V
即气体体积为原来的 0.97 倍.
考向 3 等压变化
【典题 7】(2023年河南联考)航天员出舱活动前要在节点舱(做
出舱准备的气闸舱)穿上特制的航天服,航天服内密封有一定质量
的气体(视为理想气体),密封气体的体积V1=2.4 L,压强 p1=1.0×
105 Pa,温度 t1=27 ℃.航天服内气体的平均摩尔质量 M=29 g/mol.
已知在压强 p0=1×105 Pa、温度 t0=0 ℃时,气体的摩尔体积均为
V0=22.4 L/mol.估算航天服内密封气体的质量 m(计算结果保留 3
位有效数字).
T1=273 K+27 K=300 K
T0=273 K
解得 V2=2.184 L
解得 m≈2.83 g.
考向 4 理想气体状态方程
【典题 8】(多选,2023 年新课标卷)如图所示,一封闭着
理想气体的绝热汽缸置于水平地面上,用轻弹簧连接的两绝热
活塞将汽缸分为 f、g、h 三部分,活塞与汽缸壁间没有摩擦.初始
时弹簧处于原长,三部分中气体的温度、体积、压强均相等.现通
过电阻丝对 f 中的气体缓慢加热,停止加热并达到稳定后,下列
说法正确的是(
)
A.h 中的气体内能增加
B.f 与 g 中的气体温度相等
C.f 与 h 中的气体温度相等
D.f 与 h 中的气体压强相等
解析:当电阻丝对 f 中的气体缓慢加热时,f 中的气体内能增
大,温度升高,根据理想气体状态方程可知 f 中的气体压强增大,
会缓慢推动左边活塞,可知 h 的气体体积也被压缩,压强变大,
外界对气体做正功,因为活塞和汽缸绝热,由热力学第一定律可
知,h 中的气体内能增加,A 正确;未加热前,三部分中气体的温
度、体积、压强均相等,当系统稳定时,活塞受力平衡,可知弹
错误;在达到稳定过程中 h 中的气体体积变小,压强变大,f 中的气
体体积变大.由于稳定时弹簧保持平衡状态,故稳定时 f、h 中的气
联立可得 Tf >Th,C 错误,D 正确.
答案:AD
热点 4 用图像法分析气体的状态变化
[热点归纳]
1.利用垂直于坐标轴的线作辅助线去分析同质量、不同温度的
两条等温线,不同体积的两条等容线,不同压强的两条等压线的
关系.
例如:在图甲中,V1 对应虚线为等容线,A、B 分别是虚线
与 T2、T1 两线的交点,可以认为从 B 状态通过等容升压到 A状
态,温度必然升高,所以 T2>T1.
又如图乙所示,A、B 两点的温度相等,从 B 状态到 A 状态压
强增大,体积一定减小,所以 V2甲
乙
2.关于一定质量的气体的不同图像的比较:
(续表)
【典题 9】(2022 年天津卷)某同学探究一封闭汽缸内理想气
体的状态变化特性,得到压强 p 随温度 t 的变化如图所示.已知图
线Ⅰ描述的是体积为 V1 的等容过程,当温度为
t1 时气体的压强为 p1.图线Ⅱ描述的是压强为 p2
的等压过程.取 0 ℃为 273 K,求:
(1)等容过程中,温度为 0 ℃时气体的压强.
(2)等压过程中,温度为 0 ℃时气体的体积.
方法总结 气体状态变化的图像的应用技巧
(1)明确点、线的物理意义:求解气体状态变化的图像问题,
应当明确图像上的点表示一定质量的理想气体的一个平衡状态,
它对应着三个状态参量;图像上的某一条直线段或曲线段表示一
定质量的理想气体状态变化的一个过程.
(2)明确斜率的物理意义:在 V-T 图像(或 p-T 图像)中,比较两
个状态的压强(或体积)大小,可以比较这两个状态到原点连线的斜
率的大小,其规律是斜率越大,压强(或体积)越小;斜率越小,压
强(或体积)越大.
热点 5 “两团气”模型
[热点归纳]
模型解题思路:
(1)分析“两团气”初状态和末状态的压强关系.
(2)分析“两团气”的体积及其变化关系.
(3)分析“两团气”状态参量的变化特点,选取合适的实验定
律列方程.
【典题10】(2024 年广东卷)差压阀可控制气体进行单向流动,
广泛应用于减震系统.如图所示,A、B两个导热良好的气缸通过差压阀连接,A内轻质活塞的上方与大气连通,B内气体体积不变.当A内气体压强减去B内气体压强大于Δp时差压阀打开,A内气体缓慢进入B中;当该差值小于或等于Δp时差压阀关闭.当环境温度T1=300 K时,A内气体体积VA1=4.0×10-2m3,B内气体压强pB1 等于大气压强p0,已知活塞的横截面积S=0.10 m2,Δp=0.11p0,p0=1.0×105 Pa,重力加速度大小取g=10 m/s2,A、B内的气体可视为理想气体,忽略活塞与气缸间的摩擦,差压阀与连接管内的气体体积不计.当环境温度降到T2=270 K时:
(1)求 B 内气体压强 pB2.
(2)求 A 内气体体积 VA2.
(3)在活塞上缓慢倒入铁砂,若 B 内气体压强回到 p0 并保持不
变,求已倒入铁砂的质量 m.
热点 6 探究等温情况下一定质量气体压强与体积的关系
注意事项:(1)为了保持封闭气体的质量不变,实验中采取的
主要措施是注射器活塞上涂润滑油.
(2)为了保持封闭气体的温度不变,实验中采取的主要措施是
移动活塞要缓慢和不能用手握住注射器封闭气体部分.
【典题 11】(2023 年山东卷)利用如图甲所示实验装置可探究
等温条件下气体压强与体积的关系.将带有刻度的注射器竖直固定
在铁架台上,注射器内封闭一定质量的空气,下端通过塑料管与
压强传感器相连.活塞上端固定一托盘,托盘中放入砝码,待气体
状态稳定后,记录气体压强 p 和体积 V(等于注射器示数 V0与塑料
管容积ΔV 之和),逐次增加砝码质量,采集多组数据并作出拟合
曲线如图乙所示.
甲
乙
B.p 与 成正比
回答以下问题:
(1)在实验误差允许范围内,图乙中的拟合曲线为一条过原点
的直线,说明在等温情况下,一定质量的气体________(填字母).
A.p 与 V 成正比
1
V
(2)若气体被压缩到 V=10.0 mL,由图乙可读出封闭气体压强
为__________Pa(保留 3 位有效数字).
(3)某组同学进行实验时,一同学在记录数据时漏掉了ΔV,则
在计算 pV 乘积时,他的计算结果与同组正确记录数据同学的计算
结果之差的绝对值会随 p 的增大而__________(填“增大”或“减
小”).
解析:(1)在实验误差允许范围内,图乙中的拟合曲线为一条
比,选 B.
由图乙可读出封闭气体压强为 p=2.04×105 Pa.
(3)某组同学进行实验时,一同学在记录数据时漏掉了ΔV,则
在计算 pV 乘积时,根据 p(V0+ΔV)-pV0=pΔV,可知他的计算结
果与同组正确记录数据同学的计算结果之差的绝对值会随 p 的增
大而增大.
答案:(1)B (2)2.04×105 (3)增大
抽气、打气、灌气模型
常见以下三种类型:
1.充气(打气)问题:在充气(打气)时,将充进容器内的气体和
容器内的原有气体作为研究对象时,这些气体的质量是不变的.这
样,可将“变质量”的问题转化成“定质量”问题.
2.抽气问题:在对容器抽气的过程中,对每一次抽气而言,气
体质量发生变化,解决该类变质量问题的方法与充气(打气)问题类
似——假设把每次抽出的气体包含在气体变化的始末状态中,即
用等效法把“变质量”问题转化为“定质量”的问题.
3.灌气(气体分装)问题:将一个大容器里的气体分装到多个小
容器中的问题也是“变质量”问题,分析这类问题时,可以把大
容器中的气体和多个小容器中的气体作为一个整体来进行研究,
即可将“变质量”问题转化为“定质量”问题.
【典题 12】(2023 年山东烟台二模)舱外航天服有一定的伸缩
性,能封闭一定的气体,提供人体生存的气压.2021 年 11 月 8 日,
王亚平身穿我国自主研发的舱外航天服“走出”太空舱,成为我
国第一位在太空“漫步”的女性(如图所示).王亚平先在节点舱
(出舱前的气闸舱)穿上舱外航天服,若航天服内密闭气体的体
积为 V1=2 L,压强 p1=5.0×104 Pa,温度 t1=27 ℃.然后把节点舱
的气压不断降低,到能打开舱门时,航天服内密闭气体的体积膨
胀到 V2=2.5 L,温度为 t2=-3 ℃,压强为 p2(未知).为便于舱外
活动,宇航员出舱前将一部分气体缓慢放出,使航天服内密闭气
体的体积变为 V1,气压降到 p3=3.0×104 Pa,假设释放气体过程
中温度不变.求:
(1)压强 p2.
(2)航天服需要放出的气体与原来航天服内密闭气体的质量之
比
Δm
m
.
解:(1)由题意可知,密闭航天服内气体初、末状态温度分别
为 T1=273+t1=300 K,T2=273+t2=270 K
解得 p2=3.6×104 Pa.
(2)设航天服需要放出的气体在压强为 p3 状态下的体积为ΔV,
根据玻意耳定律有
p2V2=p3(V1+ΔV)
解得ΔV=1 L
则放出的气体与原来密闭气体的质量之比为
第2节
气体
液体
固体
一、气体的性质
平均动能
容积
1.气体的状态参量.
(1)温度:在宏观上表示物体的冷热程度;在微观上是分子
____________的标志.
(2)体积:气体总是充满它所在的容器,所以气体的体积总是
等于盛装气体的容器的________.
频繁碰撞
(3)压强:气体的压强是由于气体分子____________器壁而产
生的.
2.气体分子动理论.
(1)气体分子运动的特点.
大
它能达到的整个空间
①气体分子间距较______,分子力可以忽略,因此分子间除
碰撞外不受其他力的作用,故气体能充满_____________________.
②分子做无规则的运动,速率有大有小,且时而变化,大量
分子的速率按“__________,__________”的规律分布.
③温度升高时,速率小的分子数________,速率大的分子数
________,分子的平均速率将________,但速率分布规律不变.
中间多
两头少
减少
增多
增大
(2)气体压强的微观意义.
气体的压强是大量分子频繁碰撞器壁产生的.压强的大小跟两
个因素有关:①气体分子的________;②气体分子的_________.
平均动能
密集程度
项目 玻意耳定律 查理定律 盖-吕萨克定律
内容 一定质量的某种
气体,在温度不变
的情况下,压强与
体积成①_______ 一定质量的某种气
体,在体积不变的情
况下,压强与热力学
温度成②_____ 一定质量的某种
气体,在压强不变
的情况下,其体积
与热力学温度成
③________
3.气体实验定律.
反比
正比
正比
项目 玻意耳定律 查理定律 盖-吕萨克定律
表达式 ④__________ ⑤__________
或⑥________ ⑦__________
或⑧__________
图像
(续表)
p1V1=p2V2
4.理想气体的状态方程.
pV
T
一定质量的理想气体的状态方程:_______=C(恒量).
项目 晶体 非晶体
单晶体 多晶体
外形 规则 ①________
熔点 确定 不确定
物理性质 各向
②______性 各向③______性
原子排列 规则,但多晶体每个晶粒间的
排列无规则 无规则
二、固体和液体
1.晶体和非晶体.
不规则
异
同
项目 晶体 非晶体
单晶体 多晶体
形成与
转化 有的物质在不同条件下能够形成不同的④________;
同一物质可能以⑤__________ 和⑥________ 两种不
同的形态出现;有些⑦______在一定的条件下也可转
化为⑧________
典型物质 石英、云母、食盐、硫酸铜 玻璃、蜂蜡、松香
(续表)
晶体
晶体
非晶体
晶体
非晶体
注意:多晶体没有确定的几何形状,且多晶体是各向同性的.
2.液体、液晶.
吸引
(1)液体的表面张力.
液体表面各部分间相互________的力叫表面张力.表面张力使
液体自动收缩,液体表面有收缩到最小的趋势.表面张力的方向和
液面相切;其大小除了跟边界线的长度有关外,还跟液体的种类、
温度有关.
(2)液晶的特性.
异
流动性
液体
①液晶分子既保持排列有序而显示各向______性,又可以自
由移动位置,保持了液体的____________.
②液晶分子的位置无序使它像_______,排列有序使它像晶体.
③液晶分子的排列从某个方向看比较整齐,从另一个方向看
则是杂乱无章的.
④液晶的物理性质很容易在外界的影响下发生改变.
【基础自测】
1.判断下列题目的正误.
(1)晶体有天然规则的几何形状,是因为晶体的物质微粒是规
则排列的.(
)
(2)单晶体的所有物理性质都是各向异性的.(
)
(3)多晶体和非晶体的物理性质都是各向同性的.(
)
(4)液晶是液体和晶体的混合物.(
)
(5)小船浮于水面上不是由于液体的表面张力.(
)
答案:(1)√ (2)× (3)√ (4)× (5)√
2.“嫦娥五号”探测器顺利完成月球采样任务并返回地球.
探测器上装有用石英制成的传感器,其受压时表面会产生大小
相等、符号相反的电荷——压电效应.如图所示,石英晶体沿垂
直于 x 轴晶面上的压电效应最显著.下列
)
关于石英晶体说法正确的是(
A.没有确定的熔点
B.具有各向同性的压电效应
C.没有确定的几何形状
D.是单晶体
答案:D
3.对一定质量的气体,若用 N 表示单位时间内与器壁单位面
积碰撞的分子数,则下列说法正确的是(
)
A.当体积减小时,N 必定增加
B.当温度升高时,N 必定增加
C.当压强不变而体积和温度变化时,N 必定变化
D.当体积不变而压强和温度变化时,N 可能不变
解析:气体的体积减小或温度升高时,压强和温度是怎样变
化的并不清楚,不能判断 N 是必定增加的,A、B 错误;当压强不
变而体积和温度变化时,存在两种变化的可能性:一是体积增大
时,温度升高,分子的平均动能变大,即分子对器壁碰撞的力度
增大,因压强不变,因此对器壁碰撞的频繁度降低,就是 N 减小.
二是体积减小时,温度降低,同理可推知 N 增大,C 正确,D 错
误.
答案:C
4.一定质量的气体在温度保持不变的情况下,压强增大到原来
的 4 倍,则气体的体积变为原来的(
)
A.4
B.2
C.
1
2
1
D.
4
答案:D
热点 1 固体与液体的性质
考向 1 固体的性质
[热点归纳]
晶体和非晶体.
(1)单晶体具有各向异性,但不是在各种物理性质上都表现出
各向异性.
(2)只要是具有各向异性的物体必定是晶体,且是单晶体.
(3)只要是具有确定熔点的物体必定是晶体,反之,必是非晶
体.
(4)晶体和非晶体在一定条件下可以相互转化.
【典题 1】(多选)玻璃的出现和使用在人类生活里已有四千多
)
年的历史,它是一种非晶体.下列关于玻璃的说法正确的有(
A.没有固定的熔点
B.天然具有规则的几何形状
C.沿不同方向的导热性能相同
D.分子在空间上周期性排列
解析:根据非晶体的特点可知,非晶体是指组成物质的分子(或
原子、离子)不呈空间有规则周期性排列的固体.它没有一定规则的
外形.它的物理性质在各个方向上是相同的,叫“各向同性”.它没
有固定的熔点, AC 正确.
答案:AC
形成原因 表面层中分子间的距离比液体内部分子间的距离大,
分子间的相互作用力表现为引力
表面特性 表面层分子间的引力使液面产生了表面张力,使液体
表面好像一层绷紧的弹性薄膜
考向 2 液体的性质
[热点归纳]
液体表面张力.
表面张力
的方向 和液面相切,垂直于液面上的各条分界线
表面张力
的效果 表面张力使液体表面具有收缩趋势,使液体表面积趋
于最小,而在体积相同的条件下,球形的表面积最小
(续表)
【典题 2】往两个玻璃杯中分别注入水和水银,液面出现如
图所示现象,下列说法正确的是( )
A.水不浸润玻璃
B.水银浸润玻璃
C.玻璃分子对附着层内水分子的吸引力大
于水内部分子之间的吸引力
D.玻璃分子对附着层内水银分子的吸引力
大于水银内部分子之间的吸引力
解析:水浸润玻璃,水银不浸润玻璃,浸润与否关键看附着
层的分子间距与液体分子间距比较,如果附着层中的分子密度大
( 即容器壁对液体分子的吸引力大于液
体分子对液体分子的吸引力),则表现为
附着层中的分子作用力表现为斥力,使
得液面张开,表现为浸润现象,反之相
同分析,可以如图所示理解.
答案:C
热点 2 气体压强的产生与计算
考向 1 压强的产生
[热点归纳]
1.产生的原因:气体的压强是大量分子频繁地碰撞器壁而产生
的,单个分子碰撞器壁的冲力是短暂的,但大量分子频繁地碰撞
器壁,对器壁就产生了持续、平均的作用力,数值上气体压强等
于大量分子作用在器壁单位面积的平均作用力.
2.决定因素:
(1)从宏观上看,气体压强由体积和温度决定.
(2)从微观上看,气体压强由气体分子的密集程度和平均动能
决定.
A.是由气体分子间的相互作用力(吸引和排斥)产生的
B.是由大量气体分子频繁地碰撞器壁所产生的
C.是由气体受到的重力所产生的
D.当容器自由下落时将减小为零
解析:气体压强产生的原因:大量做无规则热运动的分子对
器壁频繁、持续地碰撞产生了气体的压强,AC 错误,B 正确;
当容器自由下落时,虽然处于失重状态,但分子热运动不会停止,
故压强不会减小为零,D 错误.
答案:ACD
方法技巧
(1)气体压强与大气压强不同,大气压强由重力而
产生,随高度增大而减小,气体压强由大量气体分子频繁碰撞器
壁而产生,大小不随高度而变化.
(2)容器内气体的压强是大量分子频繁碰撞器壁而产生的,并
非因其重力而产生.
平衡
状态 力平
衡法 选取与气体接触的液柱(或活塞)为研究对象进行受力分析,得到液柱(或活塞)的受力平衡方程,求得气体的压强
等压
面法 在连通器中,同一种液体(中间不间断)同一深度处压强相等.液体内深h处的总压强 p=p0+ρgh,p0 为液面上方的压强
考向 2 压强的计算
[热点归纳]
1.封闭气体压强的求法.
平衡
状态 液片法 选取假想的液体薄片( 自身重力不计) 为研究对
象,分析液片两侧受力情况,建立平衡方程,消
去面积,得到液片两侧压强相等方程,求得气体
的压强
加速
运动
系统 选取与气体接触的液柱(或活塞)为研究对象,进行受力分
析,利用牛顿第二定律列方程求解.
(续表)
2.气体压强计算的两类模型.
(1)活塞模型.
如图所示是最常见的封闭气体的两种方式.
甲
乙
对“活塞模型”类求压强的问题,其基本的方法就是先对
“活塞”进行受力分析,然后根据平衡条件或牛顿第二定律列方
程.图甲中活塞的质量为 m,活塞横截面积为 S,外界大气压强为
p0.由于活塞处于平衡状态,所以 p0S+mg=pS.
(2)连通器模型.
如图 所示,“U”形管竖直放置.根据帕斯卡定律可知,同
一液体中的相同高度处压强一定相等.所以气体 B 和 A 的压强关
系可由图中虚线所示的等高线联系起来.则有 pB+ρgh2=pA.
而 pA=p0+ρgh1,
所以气体 B 的压强为
pB=p0+ρg(h1-h2).
其实该类问题与“活塞模型”并没有什么本质的区别.熟练后
以上压强的关系式均可直接写出,不一定都要从受力分析入手.
【典题 4】(2021年山东淄博段考)如图所示,一个横截面
积为 S 的圆筒形容器竖直放置,容器上端放一金属圆板,金属
圆板的上表面是水平的,下表面是倾斜的,下表面与
水平面的夹角为θ,圆板的质量为 M,不计圆板与容
器内壁的摩擦.若大气压强为p0,则被圆板封闭在容器
中的气体的压强为下列选项中的(
)
·cos θ=Mg+p0S
解析:圆板的下表面是倾斜的,气体对其产生的压力应与该
面垂直.为求气体的压强,应以封闭气体的金属圆板
为研究对象,其受力分析如图所示.
由物体的平衡条件得 p
S
cos θ
解得 p=p0+
Mg
.
S
答案:D
热点 3 气体实验定律和理想气体状态方程
[热点归纳]
1.理想气体.
(1)宏观上讲,理想气体是指在任何条件下始终遵守气体实验
定律的气体,实际中气体在压强不太大、温度不太低的条件下,
可视为理想气体.
(2)微观上讲,理想气体的分子间除碰撞外无其他作用力,分
子本身没有体积,即它所占据的空间认为都是可以被压缩的空间.
2.理想气体状态方程与气体实验定律的关系.
3.两个重要的推论.
考向 1 等温变化
【典题 5】(2023 年湖北卷)如图所示,竖直放置在水平桌面
上的左右两汽缸粗细均匀,内壁光滑,横截面积分别为S、2S,
由体积可忽略的细管在底部连通.两汽缸中各有一轻质活塞将一定
质量的理想气体封闭,左侧汽缸底部与活塞用轻质细弹簧相连.初
始时,两汽缸内封闭气柱的高度均为 H,弹簧长度恰好为原长.现
往右侧活塞上表面缓慢添加一定质量的沙子,直至右侧活塞下降
汽缸足够长,汽缸内气体温度始终不变,弹簧始终在弹性限度内.
求:
(1)最终汽缸内气体的压强.
(2)弹簧的劲度系数和添加的沙子质量.
解:(1)对左右气缸内所封的气体,初态压强为 p1=p0,体积
为
V1=SH+2SH=3SH
末态压强为 p2,体积为
(2)设添加的沙子质量为 m,对右边活塞受力分析可知
mg+p0·2S=p2·2S
对左侧活塞受力分析可知
考向 2 等容变化
【典题 6】(2023 年海南卷)如图所示,某饮
料瓶内密封一定质量的理想气体,t=27 ℃时,
压强 p=1.050×105 Pa,则
(1)t′=37 ℃时,气压是多大?
(2)保持温度不变,挤压气体,使之压强与(1)
相同时,气体体积变为原来的多少倍?
解:(1)瓶内气体的始末状态的热力学温度分别为
T=(27+273) K=300 K
T′=(37+273) K=310 K
解得 p′=1.085×105 Pa.
(2)保持温度不变,挤压气体,等温变化过程,由玻意耳定律
有 pV=p′V′
解得 V′≈0.97V
即气体体积为原来的 0.97 倍.
考向 3 等压变化
【典题 7】(2023年河南联考)航天员出舱活动前要在节点舱(做
出舱准备的气闸舱)穿上特制的航天服,航天服内密封有一定质量
的气体(视为理想气体),密封气体的体积V1=2.4 L,压强 p1=1.0×
105 Pa,温度 t1=27 ℃.航天服内气体的平均摩尔质量 M=29 g/mol.
已知在压强 p0=1×105 Pa、温度 t0=0 ℃时,气体的摩尔体积均为
V0=22.4 L/mol.估算航天服内密封气体的质量 m(计算结果保留 3
位有效数字).
T1=273 K+27 K=300 K
T0=273 K
解得 V2=2.184 L
解得 m≈2.83 g.
考向 4 理想气体状态方程
【典题 8】(多选,2023 年新课标卷)如图所示,一封闭着
理想气体的绝热汽缸置于水平地面上,用轻弹簧连接的两绝热
活塞将汽缸分为 f、g、h 三部分,活塞与汽缸壁间没有摩擦.初始
时弹簧处于原长,三部分中气体的温度、体积、压强均相等.现通
过电阻丝对 f 中的气体缓慢加热,停止加热并达到稳定后,下列
说法正确的是(
)
A.h 中的气体内能增加
B.f 与 g 中的气体温度相等
C.f 与 h 中的气体温度相等
D.f 与 h 中的气体压强相等
解析:当电阻丝对 f 中的气体缓慢加热时,f 中的气体内能增
大,温度升高,根据理想气体状态方程可知 f 中的气体压强增大,
会缓慢推动左边活塞,可知 h 的气体体积也被压缩,压强变大,
外界对气体做正功,因为活塞和汽缸绝热,由热力学第一定律可
知,h 中的气体内能增加,A 正确;未加热前,三部分中气体的温
度、体积、压强均相等,当系统稳定时,活塞受力平衡,可知弹
错误;在达到稳定过程中 h 中的气体体积变小,压强变大,f 中的气
体体积变大.由于稳定时弹簧保持平衡状态,故稳定时 f、h 中的气
联立可得 Tf >Th,C 错误,D 正确.
答案:AD
热点 4 用图像法分析气体的状态变化
[热点归纳]
1.利用垂直于坐标轴的线作辅助线去分析同质量、不同温度的
两条等温线,不同体积的两条等容线,不同压强的两条等压线的
关系.
例如:在图甲中,V1 对应虚线为等容线,A、B 分别是虚线
与 T2、T1 两线的交点,可以认为从 B 状态通过等容升压到 A状
态,温度必然升高,所以 T2>T1.
又如图乙所示,A、B 两点的温度相等,从 B 状态到 A 状态压
强增大,体积一定减小,所以 V2
乙
2.关于一定质量的气体的不同图像的比较:
(续表)
【典题 9】(2022 年天津卷)某同学探究一封闭汽缸内理想气
体的状态变化特性,得到压强 p 随温度 t 的变化如图所示.已知图
线Ⅰ描述的是体积为 V1 的等容过程,当温度为
t1 时气体的压强为 p1.图线Ⅱ描述的是压强为 p2
的等压过程.取 0 ℃为 273 K,求:
(1)等容过程中,温度为 0 ℃时气体的压强.
(2)等压过程中,温度为 0 ℃时气体的体积.
方法总结 气体状态变化的图像的应用技巧
(1)明确点、线的物理意义:求解气体状态变化的图像问题,
应当明确图像上的点表示一定质量的理想气体的一个平衡状态,
它对应着三个状态参量;图像上的某一条直线段或曲线段表示一
定质量的理想气体状态变化的一个过程.
(2)明确斜率的物理意义:在 V-T 图像(或 p-T 图像)中,比较两
个状态的压强(或体积)大小,可以比较这两个状态到原点连线的斜
率的大小,其规律是斜率越大,压强(或体积)越小;斜率越小,压
强(或体积)越大.
热点 5 “两团气”模型
[热点归纳]
模型解题思路:
(1)分析“两团气”初状态和末状态的压强关系.
(2)分析“两团气”的体积及其变化关系.
(3)分析“两团气”状态参量的变化特点,选取合适的实验定
律列方程.
【典题10】(2024 年广东卷)差压阀可控制气体进行单向流动,
广泛应用于减震系统.如图所示,A、B两个导热良好的气缸通过差压阀连接,A内轻质活塞的上方与大气连通,B内气体体积不变.当A内气体压强减去B内气体压强大于Δp时差压阀打开,A内气体缓慢进入B中;当该差值小于或等于Δp时差压阀关闭.当环境温度T1=300 K时,A内气体体积VA1=4.0×10-2m3,B内气体压强pB1 等于大气压强p0,已知活塞的横截面积S=0.10 m2,Δp=0.11p0,p0=1.0×105 Pa,重力加速度大小取g=10 m/s2,A、B内的气体可视为理想气体,忽略活塞与气缸间的摩擦,差压阀与连接管内的气体体积不计.当环境温度降到T2=270 K时:
(1)求 B 内气体压强 pB2.
(2)求 A 内气体体积 VA2.
(3)在活塞上缓慢倒入铁砂,若 B 内气体压强回到 p0 并保持不
变,求已倒入铁砂的质量 m.
热点 6 探究等温情况下一定质量气体压强与体积的关系
注意事项:(1)为了保持封闭气体的质量不变,实验中采取的
主要措施是注射器活塞上涂润滑油.
(2)为了保持封闭气体的温度不变,实验中采取的主要措施是
移动活塞要缓慢和不能用手握住注射器封闭气体部分.
【典题 11】(2023 年山东卷)利用如图甲所示实验装置可探究
等温条件下气体压强与体积的关系.将带有刻度的注射器竖直固定
在铁架台上,注射器内封闭一定质量的空气,下端通过塑料管与
压强传感器相连.活塞上端固定一托盘,托盘中放入砝码,待气体
状态稳定后,记录气体压强 p 和体积 V(等于注射器示数 V0与塑料
管容积ΔV 之和),逐次增加砝码质量,采集多组数据并作出拟合
曲线如图乙所示.
甲
乙
B.p 与 成正比
回答以下问题:
(1)在实验误差允许范围内,图乙中的拟合曲线为一条过原点
的直线,说明在等温情况下,一定质量的气体________(填字母).
A.p 与 V 成正比
1
V
(2)若气体被压缩到 V=10.0 mL,由图乙可读出封闭气体压强
为__________Pa(保留 3 位有效数字).
(3)某组同学进行实验时,一同学在记录数据时漏掉了ΔV,则
在计算 pV 乘积时,他的计算结果与同组正确记录数据同学的计算
结果之差的绝对值会随 p 的增大而__________(填“增大”或“减
小”).
解析:(1)在实验误差允许范围内,图乙中的拟合曲线为一条
比,选 B.
由图乙可读出封闭气体压强为 p=2.04×105 Pa.
(3)某组同学进行实验时,一同学在记录数据时漏掉了ΔV,则
在计算 pV 乘积时,根据 p(V0+ΔV)-pV0=pΔV,可知他的计算结
果与同组正确记录数据同学的计算结果之差的绝对值会随 p 的增
大而增大.
答案:(1)B (2)2.04×105 (3)增大
抽气、打气、灌气模型
常见以下三种类型:
1.充气(打气)问题:在充气(打气)时,将充进容器内的气体和
容器内的原有气体作为研究对象时,这些气体的质量是不变的.这
样,可将“变质量”的问题转化成“定质量”问题.
2.抽气问题:在对容器抽气的过程中,对每一次抽气而言,气
体质量发生变化,解决该类变质量问题的方法与充气(打气)问题类
似——假设把每次抽出的气体包含在气体变化的始末状态中,即
用等效法把“变质量”问题转化为“定质量”的问题.
3.灌气(气体分装)问题:将一个大容器里的气体分装到多个小
容器中的问题也是“变质量”问题,分析这类问题时,可以把大
容器中的气体和多个小容器中的气体作为一个整体来进行研究,
即可将“变质量”问题转化为“定质量”问题.
【典题 12】(2023 年山东烟台二模)舱外航天服有一定的伸缩
性,能封闭一定的气体,提供人体生存的气压.2021 年 11 月 8 日,
王亚平身穿我国自主研发的舱外航天服“走出”太空舱,成为我
国第一位在太空“漫步”的女性(如图所示).王亚平先在节点舱
(出舱前的气闸舱)穿上舱外航天服,若航天服内密闭气体的体
积为 V1=2 L,压强 p1=5.0×104 Pa,温度 t1=27 ℃.然后把节点舱
的气压不断降低,到能打开舱门时,航天服内密闭气体的体积膨
胀到 V2=2.5 L,温度为 t2=-3 ℃,压强为 p2(未知).为便于舱外
活动,宇航员出舱前将一部分气体缓慢放出,使航天服内密闭气
体的体积变为 V1,气压降到 p3=3.0×104 Pa,假设释放气体过程
中温度不变.求:
(1)压强 p2.
(2)航天服需要放出的气体与原来航天服内密闭气体的质量之
比
Δm
m
.
解:(1)由题意可知,密闭航天服内气体初、末状态温度分别
为 T1=273+t1=300 K,T2=273+t2=270 K
解得 p2=3.6×104 Pa.
(2)设航天服需要放出的气体在压强为 p3 状态下的体积为ΔV,
根据玻意耳定律有
p2V2=p3(V1+ΔV)
解得ΔV=1 L
则放出的气体与原来密闭气体的质量之比为
同课章节目录
