2025秋高考物理复习第三章第3节牛顿运动定律的应用(二)课件
文档属性
| 名称 | 2025秋高考物理复习第三章第3节牛顿运动定律的应用(二)课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-05 17:38:17 | ||
图片预览











文档简介
(共42张PPT)
第3节
牛顿运动定律的应用(二)
一、运动学的图像问题
1.已知物体的运动图像,求解物体的受力情况.
2.已知物体的受力图像,求解物体的运动情况.
3.特别注意图像中的一些特殊点,如图线与横、纵坐标轴的交
点,图线的转折点,两图线的交点等所表示的物理意义.注意图线
的斜率、图线与坐标轴所围图形面积的物理意义.
二、连接体
加速度
1.两个或两个以上相互作用的物体组成的具有相同_________
的整体叫连接体.如几个物体叠放在一起,或并排挤放在一起,或
用绳子、细杆等连在一起.
2.处理连接体问题的方法.
外力
(1)整体法:把整个系统作为一个研究对象来分析的方法.不必
考虑系统内力的影响,只考虑系统受到的________.
(2)隔离法:把系统中的各个部分(或某一部分)隔离,作为一个
单独的研究对象来分析的方法.此时系统的内力就有可能成为该研
究对象的外力,在分析时要特别注意.
【基础自测】
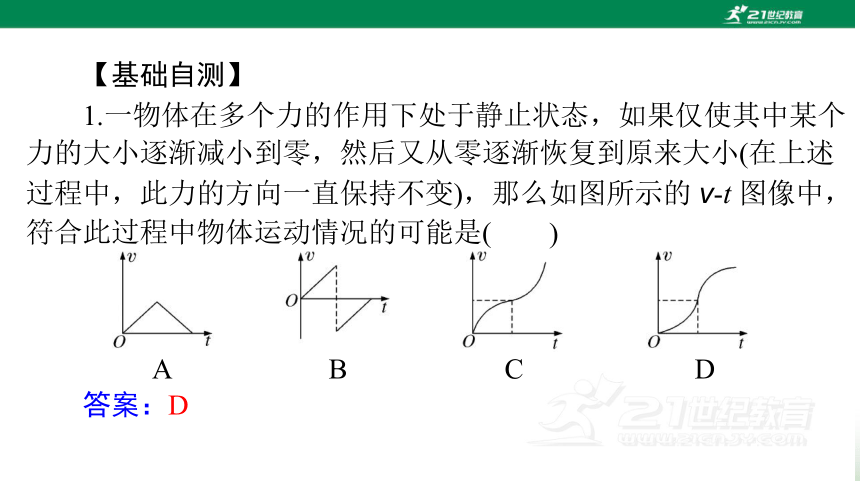
1.一物体在多个力的作用下处于静止状态,如果仅使其中某个
力的大小逐渐减小到零,然后又从零逐渐恢复到原来大小(在上述
过程中,此力的方向一直保持不变),那么如图所示的 v-t 图像中,
符合此过程中物体运动情况的可能是(
)
A
B
C
D
答案:D
2.一物体静止在光滑水平面上,从 0 时刻起,受到的水平外
力F 如图所示,以向右运动为正方向,物体质量为 1.25 kg,则
下列说法正确的是(
)
A.2 s 时物体回到出发点
B.3 s 时物体的速度大小为 4 m/s
C.第 3 s 内物体的位移为 4 m
D.前 2 s 内物体的平均速度为 0
答案:B
3.如图,小车以加速度 a 向右匀加速运动,车中小球质量
B.m(a+g)
D.ma
为 m,则线对球的拉力大小为( )
C.mg
答案:A
4.如图所示,质量为 2m 的物块 A 与水平地面间的动摩擦
因数为μ,质量为 m 的物块 B 与地面的摩擦不计,在大小为 F
的水平推力作用下,A、B 一起向右做加速运动,则 A 和 B 之间
的作用力大小为(
)
A.
μmg
3
B.
2μmg
3
2F-4μmg
C.
3
F-2μmg
D.
3
答案:D
热点 1 牛顿第二定律的图像问题
[热点归纳]
1.明确常见图像的意义,如下表.
v t 图像 根据图像的斜率判断加速度的大小和方向,进而根据牛顿第二定律求解合外力
F-a 图像 首先要根据具体的物理情景,对物体进行受力分析,然
后根据牛顿第二定律推导出两个量间的函数关系式,根
据函数关系式结合图像,明确图像的斜率、截距或面积
的意义,从而由图像给出的信息求出未知量
a-t 图像 要注意加速度的正负,正确分析每一段的运动情况,然
后结合物体受力情况根据牛顿第二定律列方程
F-t 图像 要结合物体受到的力,根据牛顿第二定律求出加速度,
分析每一时间段的运动性质
(续表)
2.图像类问题的实质是力与运动的关系问题,以牛顿第二定律
F=ma 为纽带,理解图像的种类,图像的轴、点、线、截距、斜
率、面积所表示的意义.运用图像解决问题一般包括两个角度:
(1)用给定图像解答问题.
(2)根据题意作图,用图像解答问题.在实际的应用中要建立物
理情景与函数、图像的相互转换关系.
【典题 1】(多选,2021 年广东揭阳质检)如图甲所示,一个
质量为 3 kg 的物体放在粗糙水平地面上,从零时刻起,物体在
水平力 F 作用下由静止开始做直线运动.在 0~3 s 时间内物体的
加速度 a 随时间 t 的变化规律如图乙所示,则(
)
甲
乙
A.0~1 s 和 2~3 s 内物体加速度方向相同
B.F 的最大值为 12 N
C.3 s 末物体的速度最大,最大速度为 8 m/s
D. 在 0 ~1 s 内物体做匀加速运动,2 ~3 s 内物体做匀减速
运动
答案:AC
思路导引
滑动摩擦力恒定,加速度最大时,合外力最大,
拉力最大,由于本题摩擦力未知,拉力 F 的最大值得不到具体数
据,得到拉力的关系式后定性分析判断 B 选项的正误.
【迁移拓展】(多选,2024 年广东深圳一模)如图所示,一顶
端带有挡板 P,表面粗糙的斜面固定在水平面上,滑块以速度 v0
冲上斜面,t1时刻滑到斜面顶端与挡板P发生碰撞,碰撞时间极短,
碰撞前后速度大小不变,方向相反.滑块的加速度为 a,速度为 v,
运动时间为t,以沿斜面向上为正方向.在斜面上运动的过程中,其
v-t 图像或 a-t 图像可能正确的有(
)
A
B
C
D
解析:以向上为正方向,由于接触面粗糙,受力分析可知,
答案:ACD
向上运动时,以加速度a1=gsin θ+μgcos θ进行减速,碰撞后向下运动,有三种情况:①若μmgcos θ>mgsin θ,则以加速度a2=μgcos θ-gsin θ,向下减速,可能减到零,也可能减不到零,其中a2热点 2 动力学的连接体问题
[热点归纳]
1.两个或两个以上相互作用的物体组成的系统统称连接体,连
接体问题是高考中的常考点.命题特点如下:
(1)通过轻绳、轻杆、轻弹簧关联:一般考查两物体或多物体
的平衡或共同运动,要结合绳、杆、弹簧特点分析.
(2)两物块叠放:叠放问题一般通过摩擦力的相互作用关联,
考查共点力平衡或牛顿运动定律的应用.
(3)通过滑轮关联:通过滑轮关联的两个或多个物体组成的系
统,一般是物体加速度大小相同、方向不同,可分别根据牛顿第
二定律建立方程,联立求解.
2.解决连接体问题的两种方法
考向 1 加速度相同的连接体
【典题 2】(2023 年北京卷)如图所示,在光滑水平地面上,
两相同物块用细线相连,两物块的质量均为 1 kg,细线能承受
的最大拉力为 2 N.若在水平拉力 F 作用下,两物块一起向右做
)
匀加速直线运动.则 F 的最大值为(
A.1 N
B.2 N
C.4 N
D.5 N
解析:对两物块整体做受力分析有 F=2ma,
再对于后面的物块有 FTmax=ma,FTmax=2 N,
联立解得 F=4 N,C正确.
答案:C
考向 2 加速度大小相同方向不同的连接体
【典题3】(2024 年全国甲卷)如图,一轻绳跨过光滑定滑轮,
绳的一端系物块 P,P置于水平桌面上,与桌面间存在摩擦;绳的
另一端悬挂一轻盘(质量可忽略),盘中放置砝码.改变盘中砝码总
质量 m,并测量 P 的加速度大小 a,得到 a-m 图像.重力加速度大
小为 g.在下列 a-m 图像中,可能正确的是(
)
A
B
C
D
解析:设 P 的质量为 M,P 与桌面的动摩擦力为 f;以 P 为对
象,根据牛顿第二定律可得 T-f=Ma,以盘和砝码为对象,根据
知,a-m 不是线性关系,AC 错误;可知当砝码的重力小于物块 P
最大静摩擦力时,物块和砝码静止,加速度为 0,当砝码重力大于
f 时,才有一定的加速度,当 m 趋于无穷大时,加速度趋近等于 g,
C 错误,D 正确.
答案:D
思路导引
本题与牛顿第二定律实验中的一个考点一致:当
m M 时,加速度与 m 成正比,不满足此条件时,加速度随着 m
的增加而增加,是正相关,但不能表示成正比,当 M 可以忽略时,
m的加速度为重力加速度,结合实际情况,加速度只能无限接近重
力加速度,但不可能等于重力加速度.
,重力加速度大小为
考向 3 加速度大小方向均不同的连接体
【典题 4】(多选,2023 年安徽合肥模拟)如图所示,质量
为 M、倾角为 30°的斜面体置于水平地面上,一轻绳绕过两个
轻质滑轮连接着固定点P和物体B,两滑轮之间的轻绳始终与斜面
平行,物体 A、B 的质量分别为 m、2m,A 与
斜面间的动摩擦因数为
g,将 A、B 由静止释放,在B下降的过程中(物
体 A 未碰到滑轮),斜面体静止不动.下列说法
正确的是(
)
解析:由于相同时间内物体 B 通过的位移是物体 A 通过的位
移的两倍,则物体 B 的加速度是物体 A 的加速度的两倍;设物体
A 的加速度为 a,则 B 的加速度为 2a;设物体 A、B 释放瞬间,
轻绳的拉力为 T,根据牛顿第二定律得2T-mgsin 30°-μmgcos 30°
A 正确,B 错误;物体 B 下降过程中,对斜面体、A、B 整体,水平
方向根据牛顿第二定律得 Tcos 30°-f=macos 30°,解得地面对
答案:AC
动力学中的临界极值问题
[热点归纳]
1.临界或极值条件的标志.
(1)有些题目中有“刚好”“恰好”“正好”等字眼,表明题
述的过程存在临界点.
(2)若题目中有“取值范围”“多长时间”“多大距离”等词
语,表明题述的过程存在“起止点”,而这些起止点往往就对应
临界状态.
(3)若题目中有“最大”“最小”“至多”“至少”等字眼,
表明题述的过程存在极值,这个极值点往往是临界点.
(4)若题目要求“最终加速度”“稳定速度”等,即求收尾加
速度或收尾速度.
临界状态 临界条件
速度达到最大 物体所受的合外力为零
两物体刚好分离 两物体间的弹力 FN=0
绳刚好被拉直 绳中张力为零
绳刚好被拉断 绳中张力等于绳能承受的最大拉力
2.几种临界状态和其对应的临界条件如下表所示.
极限法 把物理问题(或过程)推向极端,从而使临界现象(或状态)
暴露出来,以达到正确解决问题的目的
假设法 临界问题存在多种可能,特别是非此即彼两种可能时,或
变化过程中可能出现临界条件,也可能不出现临界条件
时,往往用假设法解决问题
数学法 将物理过程转化为数学表达式,根据数学表达式解出临界
条件
3.处理临界问题的三种方法.
模型一 动力学中的临界问题
【典题 5】(2023 年福建厦门开学考)如图所示,在光滑水
平地面上有一个质量M=2 kg、倾角θ=37°的光滑斜劈A,在钉
在劈端的钉子上系着一条轻线,线下端拴着一个质量 m=1 kg 的
小球 B.用图示方向的水平恒力 F 拉斜劈,已知重力加速度大小为
g 取 10 m/s2,sin 37°=0.6,cos 37°=0.8.(计算结果可保留分数、
根号)
(1)若 B 与 A 之间恰好无挤压时,求 B 的加速度大小以及拉力
F 的大小.
(2)若 F=24 N,求此时绳对球的拉力大小.
(3)若 F=45 N,求此时绳对球的拉力大小.
解:(1)当小球与斜劈之间恰好无挤压时,对小球受力进行正
交分解,可得 T sin θ=mg,T cos θ=ma
解得 a=
40
3
m/s2
对整体有 F=(m+M)a
解得此时拉力 F 的大小 F=40 N.
(2)因为 F=24 N<40 N,小球没脱离斜面,根据平衡条件得
Tsin 37°+FNcos 37°=mg
根据牛顿第二定律得
Tcos 37°-FNsin 37°=ma
F=(m+M)a
解得此时绳对球的拉力大小 T=12.4 N.
(3)因为 F=45 N>40 N
小球与斜面间无弹力,对整体有 F=(m+M)a
模型二 动力学中的极值问题
【典题 6】如图所示,一质量 m=0.4 kg 的小物块,以v0=
2 m/s 的初速度在与斜面成某一夹角的拉力 F 作用下,沿斜面
向上做匀加速运动,经 t=2 s 的时间物块由 A 点运动到 B 点,A、
B 之间的距离 L=10 m.已知斜面倾角θ=30°,物块与斜面之间的
(1)求物块加速度的大小及到达 B 点时速度的大小.
(2)拉力 F 与斜面夹角为多大时,拉力 F 最小?拉力 F 的最小
值是多少?
解:(1)设物块加速度的大小为 a,到达 B点时速度的大小为 v,
由运动学公式得
v=v0+at ②
联立①②式,代入数据得
a=3 m/s2 ③
v=8 m/s. ④
(2)设物块所受支持力为 FN,所受摩擦力为 Ff,拉力 F 与斜面
间的夹角为α,受力分析如图所示,由牛顿第二定律得
Fcos α-mgsin θ-Ff=ma ⑤
Fsin α+FN-mgcos θ=0 ⑥
又 Ff=μFN ⑦
联立⑤⑥⑦式得
F=
mg(sin θ+μcos θ)+ma
cos α+μsin α
⑧
由数学知识得
由⑧⑨式可知对应最小 F 的夹角
α=30° ⑩
联立③⑧⑩式,代入数据得 F 的最小值为
第3节
牛顿运动定律的应用(二)
一、运动学的图像问题
1.已知物体的运动图像,求解物体的受力情况.
2.已知物体的受力图像,求解物体的运动情况.
3.特别注意图像中的一些特殊点,如图线与横、纵坐标轴的交
点,图线的转折点,两图线的交点等所表示的物理意义.注意图线
的斜率、图线与坐标轴所围图形面积的物理意义.
二、连接体
加速度
1.两个或两个以上相互作用的物体组成的具有相同_________
的整体叫连接体.如几个物体叠放在一起,或并排挤放在一起,或
用绳子、细杆等连在一起.
2.处理连接体问题的方法.
外力
(1)整体法:把整个系统作为一个研究对象来分析的方法.不必
考虑系统内力的影响,只考虑系统受到的________.
(2)隔离法:把系统中的各个部分(或某一部分)隔离,作为一个
单独的研究对象来分析的方法.此时系统的内力就有可能成为该研
究对象的外力,在分析时要特别注意.
【基础自测】
1.一物体在多个力的作用下处于静止状态,如果仅使其中某个
力的大小逐渐减小到零,然后又从零逐渐恢复到原来大小(在上述
过程中,此力的方向一直保持不变),那么如图所示的 v-t 图像中,
符合此过程中物体运动情况的可能是(
)
A
B
C
D
答案:D
2.一物体静止在光滑水平面上,从 0 时刻起,受到的水平外
力F 如图所示,以向右运动为正方向,物体质量为 1.25 kg,则
下列说法正确的是(
)
A.2 s 时物体回到出发点
B.3 s 时物体的速度大小为 4 m/s
C.第 3 s 内物体的位移为 4 m
D.前 2 s 内物体的平均速度为 0
答案:B
3.如图,小车以加速度 a 向右匀加速运动,车中小球质量
B.m(a+g)
D.ma
为 m,则线对球的拉力大小为( )
C.mg
答案:A
4.如图所示,质量为 2m 的物块 A 与水平地面间的动摩擦
因数为μ,质量为 m 的物块 B 与地面的摩擦不计,在大小为 F
的水平推力作用下,A、B 一起向右做加速运动,则 A 和 B 之间
的作用力大小为(
)
A.
μmg
3
B.
2μmg
3
2F-4μmg
C.
3
F-2μmg
D.
3
答案:D
热点 1 牛顿第二定律的图像问题
[热点归纳]
1.明确常见图像的意义,如下表.
v t 图像 根据图像的斜率判断加速度的大小和方向,进而根据牛顿第二定律求解合外力
F-a 图像 首先要根据具体的物理情景,对物体进行受力分析,然
后根据牛顿第二定律推导出两个量间的函数关系式,根
据函数关系式结合图像,明确图像的斜率、截距或面积
的意义,从而由图像给出的信息求出未知量
a-t 图像 要注意加速度的正负,正确分析每一段的运动情况,然
后结合物体受力情况根据牛顿第二定律列方程
F-t 图像 要结合物体受到的力,根据牛顿第二定律求出加速度,
分析每一时间段的运动性质
(续表)
2.图像类问题的实质是力与运动的关系问题,以牛顿第二定律
F=ma 为纽带,理解图像的种类,图像的轴、点、线、截距、斜
率、面积所表示的意义.运用图像解决问题一般包括两个角度:
(1)用给定图像解答问题.
(2)根据题意作图,用图像解答问题.在实际的应用中要建立物
理情景与函数、图像的相互转换关系.
【典题 1】(多选,2021 年广东揭阳质检)如图甲所示,一个
质量为 3 kg 的物体放在粗糙水平地面上,从零时刻起,物体在
水平力 F 作用下由静止开始做直线运动.在 0~3 s 时间内物体的
加速度 a 随时间 t 的变化规律如图乙所示,则(
)
甲
乙
A.0~1 s 和 2~3 s 内物体加速度方向相同
B.F 的最大值为 12 N
C.3 s 末物体的速度最大,最大速度为 8 m/s
D. 在 0 ~1 s 内物体做匀加速运动,2 ~3 s 内物体做匀减速
运动
答案:AC
思路导引
滑动摩擦力恒定,加速度最大时,合外力最大,
拉力最大,由于本题摩擦力未知,拉力 F 的最大值得不到具体数
据,得到拉力的关系式后定性分析判断 B 选项的正误.
【迁移拓展】(多选,2024 年广东深圳一模)如图所示,一顶
端带有挡板 P,表面粗糙的斜面固定在水平面上,滑块以速度 v0
冲上斜面,t1时刻滑到斜面顶端与挡板P发生碰撞,碰撞时间极短,
碰撞前后速度大小不变,方向相反.滑块的加速度为 a,速度为 v,
运动时间为t,以沿斜面向上为正方向.在斜面上运动的过程中,其
v-t 图像或 a-t 图像可能正确的有(
)
A
B
C
D
解析:以向上为正方向,由于接触面粗糙,受力分析可知,
答案:ACD
向上运动时,以加速度a1=gsin θ+μgcos θ进行减速,碰撞后向下运动,有三种情况:①若μmgcos θ>mgsin θ,则以加速度a2=μgcos θ-gsin θ,向下减速,可能减到零,也可能减不到零,其中a2
[热点归纳]
1.两个或两个以上相互作用的物体组成的系统统称连接体,连
接体问题是高考中的常考点.命题特点如下:
(1)通过轻绳、轻杆、轻弹簧关联:一般考查两物体或多物体
的平衡或共同运动,要结合绳、杆、弹簧特点分析.
(2)两物块叠放:叠放问题一般通过摩擦力的相互作用关联,
考查共点力平衡或牛顿运动定律的应用.
(3)通过滑轮关联:通过滑轮关联的两个或多个物体组成的系
统,一般是物体加速度大小相同、方向不同,可分别根据牛顿第
二定律建立方程,联立求解.
2.解决连接体问题的两种方法
考向 1 加速度相同的连接体
【典题 2】(2023 年北京卷)如图所示,在光滑水平地面上,
两相同物块用细线相连,两物块的质量均为 1 kg,细线能承受
的最大拉力为 2 N.若在水平拉力 F 作用下,两物块一起向右做
)
匀加速直线运动.则 F 的最大值为(
A.1 N
B.2 N
C.4 N
D.5 N
解析:对两物块整体做受力分析有 F=2ma,
再对于后面的物块有 FTmax=ma,FTmax=2 N,
联立解得 F=4 N,C正确.
答案:C
考向 2 加速度大小相同方向不同的连接体
【典题3】(2024 年全国甲卷)如图,一轻绳跨过光滑定滑轮,
绳的一端系物块 P,P置于水平桌面上,与桌面间存在摩擦;绳的
另一端悬挂一轻盘(质量可忽略),盘中放置砝码.改变盘中砝码总
质量 m,并测量 P 的加速度大小 a,得到 a-m 图像.重力加速度大
小为 g.在下列 a-m 图像中,可能正确的是(
)
A
B
C
D
解析:设 P 的质量为 M,P 与桌面的动摩擦力为 f;以 P 为对
象,根据牛顿第二定律可得 T-f=Ma,以盘和砝码为对象,根据
知,a-m 不是线性关系,AC 错误;可知当砝码的重力小于物块 P
最大静摩擦力时,物块和砝码静止,加速度为 0,当砝码重力大于
f 时,才有一定的加速度,当 m 趋于无穷大时,加速度趋近等于 g,
C 错误,D 正确.
答案:D
思路导引
本题与牛顿第二定律实验中的一个考点一致:当
m M 时,加速度与 m 成正比,不满足此条件时,加速度随着 m
的增加而增加,是正相关,但不能表示成正比,当 M 可以忽略时,
m的加速度为重力加速度,结合实际情况,加速度只能无限接近重
力加速度,但不可能等于重力加速度.
,重力加速度大小为
考向 3 加速度大小方向均不同的连接体
【典题 4】(多选,2023 年安徽合肥模拟)如图所示,质量
为 M、倾角为 30°的斜面体置于水平地面上,一轻绳绕过两个
轻质滑轮连接着固定点P和物体B,两滑轮之间的轻绳始终与斜面
平行,物体 A、B 的质量分别为 m、2m,A 与
斜面间的动摩擦因数为
g,将 A、B 由静止释放,在B下降的过程中(物
体 A 未碰到滑轮),斜面体静止不动.下列说法
正确的是(
)
解析:由于相同时间内物体 B 通过的位移是物体 A 通过的位
移的两倍,则物体 B 的加速度是物体 A 的加速度的两倍;设物体
A 的加速度为 a,则 B 的加速度为 2a;设物体 A、B 释放瞬间,
轻绳的拉力为 T,根据牛顿第二定律得2T-mgsin 30°-μmgcos 30°
A 正确,B 错误;物体 B 下降过程中,对斜面体、A、B 整体,水平
方向根据牛顿第二定律得 Tcos 30°-f=macos 30°,解得地面对
答案:AC
动力学中的临界极值问题
[热点归纳]
1.临界或极值条件的标志.
(1)有些题目中有“刚好”“恰好”“正好”等字眼,表明题
述的过程存在临界点.
(2)若题目中有“取值范围”“多长时间”“多大距离”等词
语,表明题述的过程存在“起止点”,而这些起止点往往就对应
临界状态.
(3)若题目中有“最大”“最小”“至多”“至少”等字眼,
表明题述的过程存在极值,这个极值点往往是临界点.
(4)若题目要求“最终加速度”“稳定速度”等,即求收尾加
速度或收尾速度.
临界状态 临界条件
速度达到最大 物体所受的合外力为零
两物体刚好分离 两物体间的弹力 FN=0
绳刚好被拉直 绳中张力为零
绳刚好被拉断 绳中张力等于绳能承受的最大拉力
2.几种临界状态和其对应的临界条件如下表所示.
极限法 把物理问题(或过程)推向极端,从而使临界现象(或状态)
暴露出来,以达到正确解决问题的目的
假设法 临界问题存在多种可能,特别是非此即彼两种可能时,或
变化过程中可能出现临界条件,也可能不出现临界条件
时,往往用假设法解决问题
数学法 将物理过程转化为数学表达式,根据数学表达式解出临界
条件
3.处理临界问题的三种方法.
模型一 动力学中的临界问题
【典题 5】(2023 年福建厦门开学考)如图所示,在光滑水
平地面上有一个质量M=2 kg、倾角θ=37°的光滑斜劈A,在钉
在劈端的钉子上系着一条轻线,线下端拴着一个质量 m=1 kg 的
小球 B.用图示方向的水平恒力 F 拉斜劈,已知重力加速度大小为
g 取 10 m/s2,sin 37°=0.6,cos 37°=0.8.(计算结果可保留分数、
根号)
(1)若 B 与 A 之间恰好无挤压时,求 B 的加速度大小以及拉力
F 的大小.
(2)若 F=24 N,求此时绳对球的拉力大小.
(3)若 F=45 N,求此时绳对球的拉力大小.
解:(1)当小球与斜劈之间恰好无挤压时,对小球受力进行正
交分解,可得 T sin θ=mg,T cos θ=ma
解得 a=
40
3
m/s2
对整体有 F=(m+M)a
解得此时拉力 F 的大小 F=40 N.
(2)因为 F=24 N<40 N,小球没脱离斜面,根据平衡条件得
Tsin 37°+FNcos 37°=mg
根据牛顿第二定律得
Tcos 37°-FNsin 37°=ma
F=(m+M)a
解得此时绳对球的拉力大小 T=12.4 N.
(3)因为 F=45 N>40 N
小球与斜面间无弹力,对整体有 F=(m+M)a
模型二 动力学中的极值问题
【典题 6】如图所示,一质量 m=0.4 kg 的小物块,以v0=
2 m/s 的初速度在与斜面成某一夹角的拉力 F 作用下,沿斜面
向上做匀加速运动,经 t=2 s 的时间物块由 A 点运动到 B 点,A、
B 之间的距离 L=10 m.已知斜面倾角θ=30°,物块与斜面之间的
(1)求物块加速度的大小及到达 B 点时速度的大小.
(2)拉力 F 与斜面夹角为多大时,拉力 F 最小?拉力 F 的最小
值是多少?
解:(1)设物块加速度的大小为 a,到达 B点时速度的大小为 v,
由运动学公式得
v=v0+at ②
联立①②式,代入数据得
a=3 m/s2 ③
v=8 m/s. ④
(2)设物块所受支持力为 FN,所受摩擦力为 Ff,拉力 F 与斜面
间的夹角为α,受力分析如图所示,由牛顿第二定律得
Fcos α-mgsin θ-Ff=ma ⑤
Fsin α+FN-mgcos θ=0 ⑥
又 Ff=μFN ⑦
联立⑤⑥⑦式得
F=
mg(sin θ+μcos θ)+ma
cos α+μsin α
⑧
由数学知识得
由⑧⑨式可知对应最小 F 的夹角
α=30° ⑩
联立③⑧⑩式,代入数据得 F 的最小值为
同课章节目录
