2025秋高考物理复习第二章第3节受力分析共点力的平衡课件
文档属性
| 名称 | 2025秋高考物理复习第二章第3节受力分析共点力的平衡课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-05 17:39:30 | ||
图片预览











文档简介
(共69张PPT)
第3节
受力分析
共点力的平衡
一、受力分析
受力
1.定义:把指定物体(或研究对象)在特定的物理环境中受到的
所有外力都分析出来,并画出物体____________的示意图的过程.
2.受力分析步骤.
(1)选取对象:研究对象可以是质点、结点、某个物体,或几
个物体组成的系统.原则上使问题的研究处理尽量简便.
(2)按顺序找力:先把研究对象从周围环境中隔离出来,再按
照性质力的顺序逐一分析:先分析________(重力、电场力、磁场
力),再分析__________(弹力、摩擦力),最后分析其他力.
(3)画出受力示意图:把物体所受的力一一画在受力图上,并
标明各力的方向,注意不要将施出的力画在图上.
(4)检验:防止错画、漏画、多画力.
场力
接触力
特别提醒:弹力、摩擦力的产生条件之一都是接触,因此在
分析这两种力时先找接触面,在每个接触面上逐一分析这两种力.
二、共点力的平衡
1.平衡状态.
物体处于______状态或________________状态.
2.平衡条件.
静止
匀速直线运动
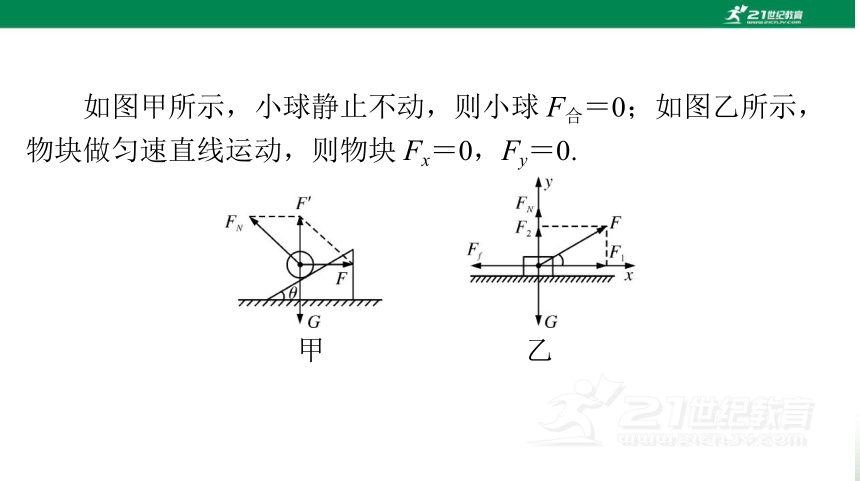
如图甲所示,小球静止不动,则小球 F合=0;如图乙所示,
物块做匀速直线运动,则物块 Fx=0,Fy=0.
甲
乙
3.平衡条件的推论.
相等
相反
三角形
(1)二力平衡:如果物体在两个共点力的作用下处于平衡状态,
这两个力必定大小相等,方向相反.
(2)三力平衡:物体在三个共点力的作用下处于平衡状态,其
中任何一个力与另外两个力的合力大小______,方向______,并
且这三个力的矢量可以形成一个封闭的矢量__________.
(3)多力平衡:物体在多个共点力的作用下处于平衡状态,其
中任何一个力与另外几个力的合力大小______,方向______.
相等
相反
【基础自测】
1.判断下列题目的正误.
(1)物体的速度为零即处于平衡状态.(
)
(2)物体处于平衡状态时,其加速度一定为零.(
)
(3)物体受两个力作用处于平衡状态,这两个力必定等大反向.
(
(
)
(4) 物体处于平衡状态时,其所受的作用力必定为共点力.
)
(5)物体受三个力 F1、F2、F3 作用处于平衡状态,若将 F2 转动
)
90°,则三个力的合力大小为 F2.(
答案:(1)× (2)√ (3)√ (4)× (5)√
2.如图所示,某物体在四个共点力作用下处于平衡状态,若
将F4=5 N 的力沿逆时针方向转动 90°,其余三个力的大小和方
)
向都不变,则此时物体所受合力的大小为(
答案:C
3.如图所示,利用三根等长的轻绳以正三棱锥形将花盆竖直
悬空吊在挂钩上,下列说法正确的是( )
A.三根轻绳对花盆作用力的合力方向一定竖直向上
B.每根轻绳的拉力均为花盆重力大小的三分之一
C.若将三根轻绳缩短相同的长度,则每根轻绳的拉
力减小
D.若将三根轻绳增加相同的长度,则三根轻绳对花
盆作用力的合力增大
解析:花盆处于静止状态,由平衡条件可知,三根轻绳对花
盆作用力的合力大小等于花盆的重力大小,方向与重力的方向相
反,即竖直向上,A 正确,D 错误;设花盆的重力为 G,每根轻绳
中的拉力为 F,轻绳与竖直方向的夹角均为θ,则G=3Fcos θ,解
答案:A
4.(2022 年广东湛江模拟)如图所示,一只蚂蚁沿着向下弯成
弧面的树叶从 A 经 B 缓慢爬到 C 的过程中,下列说法正确的
是(
)
A.树枝对蚂蚁的作用力先增大后减小
B.树枝对蚂蚁的作用力先减小后增大
C.树枝对蚂蚁的摩擦力先减小后增大
D.树枝对蚂蚁的摩擦力先增大后减小
解析:树枝对蚂蚁的作用力即是树枝对蚂蚁的支持力和摩擦
力的合力,与蚂蚁的重力是一对平衡力,由于重力总竖直向下,
故这个合力也竖直向上,大小不变,AB 错误;缓慢相当于动态
平衡,设摩擦力与水平方向夹角为θ,有 f=mgsin θ,从 A 到 B,
随着θ的减小,摩擦力先减小.从 B 到 C,随着θ的增大,摩擦力再
增大,C 正确,D 错误.
答案:C
热点1 受力分析
【典题1】(多选,2024 年广东梅州期中)如图,质量均为 m
的 A、B、C 三个木块叠放在粗糙的水平地面上,A、B 接触面沿
)
水平方向,整个系统处于静止状态,下列说法正确的是(
A.A 对 B 压力的大小等于 mg
B.木块 B 受到 4 个力的作用
C.地面对 C 的摩擦力水平向左
D.地面对 C 的支持力等于 3mg
解析:对 A 受力分析可知,B 对 A 的支持力大小等于 mg,则
由牛顿第三定律可知,A 对 B 压力的大小等于 mg,A 正确;木块
B 受到重力、斜面的支持力和摩擦力以及 A 对 B 的压力共 4 个力
的作用,B 正确;对 ABC 整体分析可知,水平方向受力平衡,则
地面对 C 无摩擦力作用,竖直方向平衡可知,地面对 C 的支持力
等于 3mg,C 错误,D 正确.
答案:ABD
条件
判据 不同性质的力产生条件不同,进行受力分析时最基本的判据是根据其产生条件
效果
判据 有时候是否满足某力产生的条件是很难判定的,可先根据物体的运动状态进行
分析,再运用平衡条件或牛顿运动定律判定未知力,也可应用“假设法”.
(1)物体平衡时合外力必定为零.
(2)物体做变速运动时必定合力方向沿加速度方向,合力大小满足 F=ma.
(3)物体做匀速圆周运动时必定合外力大小恒定,满足 F= ,方向始终指向
圆心
特征
判据 在有些受力情况较为复杂的情况下,我们根据力产生的条件及其作用效果仍不
能判定该力是否存在时,可从力的作用是相互的这个基本特征出发,通过判定
其反作用力是否存在来判定该力
方法技巧 受力分析的三个常用判据
方法 基本思路 求解方法 条件
正交
分解法 变矢量运算为代数运算 将各力分解到x轴和y轴上,运用两坐标轴上的合力等于零的条件列方程求解,即∑Fx=0,∑Fy=0 三个或三个以上共点力作用下物体的平衡
热点 2 静态平衡
[热点归纳]
处理平衡问题的常用方法.
方法 基本思路 求解方法 条件
力的
合成法 通过平行四边形定则,构建矢量三角形,利用几何知识求解 物体受到三个力平衡时,任意两个力的合力与第三个力等大、反向,可以应用三角函数、相似三角形等知识求解 三力平衡
(续表)
考向 1 合成法
【典题2】(2023 年河北卷)如图,轻质细杆 AB 上穿有一个质
量为 m 的小球 C,将杆水平置于相互垂直的
固定光滑斜面上,系统恰好处于平衡状态.已
知左侧斜面与水平面成 30°角,则左侧斜面
对杆 AB 支持力的大小为(
)
答案:B
思路导引
本题与常见题目的区别是有一根轻杆,可以“无
视”杆的存在,球在重力和两个弹力的作用下处于平衡状态,弹
力的方向与斜面垂直,先找出两个弹力作用线的交点,此交点确
定“重心”的位置,然后应用三力平衡求解.
考向 2 正交分解法
【典题 3】(2022 年辽宁卷)如图所示,蜘蛛用蛛丝将其自身
悬挂在水管上,并处于静止状态.蛛丝 OM、ON 与竖直方向夹角
)
分别为α、β(α>β).用 F1、F2 分别表示 OM、ON 的拉力,则(
A.F1 的竖直分力大于 F2 的竖直分力
B.F1 的竖直分力等于 F2 的竖直分力
C.F1 的水平分力大于 F2 的水平分力
D.F1 的水平分力等于 F2 的水平分力
解析:对结点 O 受力分析可得,水平方向 F1sin α=F2sin β,
即 F1 的水平分力等于 F2 的水平分力,C 错误,D 正确;对结点
O受力分析可得,竖直方向 F1cos α+F2cos β=mg,解得 F1=
答案:D
思路导引 蛛丝 OM、ON 与竖直方向夹角分别为α、β不相
等,两角之和也不为直角,力按效果分解不适应,只能采用正交
分解的方法,将结点受的力在水平方向和竖直方向正交分解.
热点 3 共点力作用下的动态平衡
[热点归纳]
1.动态平衡:通过控制某些物理量,使物体的状态发生缓慢的
变化,而在这个过程中物体又始终处于一系列的平衡状态,在问
题的描述中常用“缓慢”等语言叙述.
图解法 对研究对象在动态变化过程中的若干状态进行受力分析,在
同一图中作出物体在若干状态下所受的力的平行四边形(或
三角形),即为图解法.此法常用于求解三力平衡且有一个力
是恒力、另有一个力方向不变的问题
相似三
角形法 物体在三力作用下动态平衡,且其中一个力的大小和方向恒
定,其他两个力的大小和方向都可变,这些变化是由物体间
距离的变化引起的,且题目还给出了有关边的长度,这时要
注意力的矢量三角形和几何三角形相似的知识运用
2.分析动态平衡问题的常用方法.
解析法 对研究对象进行受力分析,先画出受力示意图,再根据物体
的平衡条件列式求解,得到因变量与自变量的一般函数表达
式,最后根据自变量的变化确定因变量的变化
正弦
定理法 物体受到三个力的作用,其中的一个力大小、方向都不变,
另外两个力的方向都发生变化,但之间的夹角保持不变,可
利用正弦定理法分析
(续表)
3.基本思路:化“动”为“静”,“静”中求“动”.
考向 1 图解法
【典题 4】(2024 年广东佛山二模)如图,用 AB 与 AC 两根绳
悬挂一质量分布不均(重心偏左)的矩形画框,画框底部需保持与水
平地面平行.若保持 AB绳长不变,将 C 端左移,AC 绳缩短至某一
长度(但 AC 绳仍长于 AB 绳)后悬挂画框,画框保持原状态不动,
则改变 AC 绳长前后(
)
A.AB 绳的拉力大小总等于 AC 绳的拉力大小
B.AB 绳的拉力大小总小于 AC 绳的拉力大小
C.AB 绳的拉力大小不变
D.AC 绳的拉力大小可能相等
解析:对画框受力分析,如图甲所示.
甲
设 AB 绳上的拉力与水平方向的夹角为θ1,AC 绳上的拉力与
水平方向的夹角为θ,根据题意,保持 AB 绳长不变,将 C 端左移,
AC 绳缩短至某一长度(但 AC 绳仍长于 AB 绳),则可知该过程中θ1
始终不变,且根据几何关系,始终有θ1>θ2,则在水平方向根据平
衡条件有
乙
FABcos θ1=FACcos θ2,由于θ1始终大于θ2,因此FAB始终大于FAC,AB错误;重力为恒力,AB绳上力的方向始终不变,做出力的矢量三角形如图乙所示.
可知,随着 AC 绳将 C 端向左移动,绳 AC 与竖直方向的夹角
在减小,该过程中绳 AC 上的拉力可能先减小后增大,当绳 AC 垂
直于绳 AB 时,绳 AC 上的拉力有最小值,因此 AC 绳的拉力大小
可能相等,该过程中绳 AB 上的拉力 FAB 逐渐减小,但始终大于绳
AC 上的拉力 FAC,C 错误,D 正确.
答案:D
考向 2 相似三角形法
【典题5】(2024年广东深圳一模)如图所示,用一轻绳通过定
滑轮将质量为 m 的小球静置在光滑的半圆柱体上,小球的半径远
小于半圆柱体截面的半径 R,绳 AB 长度为 L,长度为 H 的杆 BC
竖直且与半圆柱体边缘相切,OA 与水平面夹角为θ,不计一切摩
擦,重力加速度为 g,下列表达式表示绳对小球的拉力 F 是(
)
A.
mgL
H
B.
mgR(1+cos θ)
(H+Rtan θ)cos θ
C.
mgL
H+Rtan θ
D.
mgLtan θ
Htan θ+R
解析:根据题意,对小球受力分析,受拉力、支持力和重力,
把拉力和支持力平移,组成矢量三角形,延长 AO 和 BC 交于 D
点,如图所示.
答案:C
思路导引
应用力的三角形与几何三角形相似,长度不变的
边对应大小不变的力,长度变化的边对应大小变化的力,即力与
对应边同趋势变化.
考向 3 解析法
【典题6】(2024 年广东惠州质检)运动会比赛结束后,教师为
参赛的运动员颁奖,我们可以把奖牌简化为一根质量不计的轻绳
和位于轻绳中点质量为 m 的重物,重物可视为质点.教师手抓在轻
绳的两端,重力加速度为 g,下列说法正确的是(
)
A.当轻绳夹角变大时,绳的张力减小
B.轻绳夹角不变,教师用力抓轻绳时,轻绳与教师手之间摩
擦力增加
D.教师双手对轻绳的作用力方向为沿绳斜向上
解析:根据题意,对小球受力分析,由平衡条件有 2Fcos θ=
变小,轻绳上拉力大小变大,轻绳夹角不变,轻绳上拉力大小不
变,由平衡条件可知,教师用力抓轻绳时,轻绳与教师手之间摩
擦力不变,AB 错误,C正确;根据题意,把轻绳和小球看做整体,
对整体受力分析,由平衡条件可知,教师双手对轻绳的作用力与
小球的重力等大反向,则教师双手对轻绳的作用力方向为竖直向
上,D 错误.
答案:C
考向 4 正弦定理法
【典题 7】(2022 年河北卷)如图,用两根等长的细绳将
一匀质圆柱体悬挂在竖直木板的 P 点,将木板以
底边 MN 为轴向后方缓慢转动直至水平,绳与木
板之间的夹角保持不变,忽略圆柱体与木板之间
的摩擦,在转动过程中(
)
A.圆柱体对木板的压力逐渐增大
B.圆柱体对木板的压力先增大后减小
C.两根细绳上的拉力均先增大后减小
D.两根细绳对圆柱体拉力的合力保持不变
解析:设两绳子对圆柱体的拉力的合力为 T,木板对圆柱体的
支持力为 N,绳子与木板夹角为 β,从右向左看如图 所示.
在矢量三角形中,根据正弦定理
在木板以直线 MN 为轴向后方缓慢转动直至水平过程中,α不
变,γ 从 90°逐渐减小到 0,又 γ+β+α=180°,且 α<90°,可
知 90°<γ+β<180°,则 0<β<180°,
sin γ不断减小,可知 T 不断减小,sin β先增大后减小,可知 N 先
增大后减小,结合牛顿第三定律可知,圆柱体对木板的压力先增
大后减小,设两绳子之间的夹角为 2θ,绳子拉力为 T′,则2T′cos θ
T
2cos θ
,θ 不变,T 逐渐减小,可知绳子拉力不断减
=T 可得 T′=
小,B 正确.
答案:B
思路导引
将两根细绳的拉力看作一个力,这样圆柱体在三
个力作用下平衡,构建力的三角形:拉力、重力、挡板的弹力。
确定该三角形中角度是否变化及变化特点:绳与木板之间的夹角
保持不变,挡板弹力与竖直方向间的夹角从 90°逐渐减小到 0,另
外一个角根据三角形内角和 180°得到,然后应用正弦定理判断力
的变化情况.
整体法与隔离法的应用
当物理情境中涉及物体较多时,就要考虑采用整体法和隔离
法.
同时满足上述两个条件即可采用整体法.
必须将物体从系统中隔离出来,单独地进行受力分析,列出
方程.
(3)整体法和隔离法的交替运用
对于一些复杂问题,比如连接体问题,通常需要多次选用研
究对象,这样整体法和隔离法要交替使用.
【典题 8】(多选,2023 年广东深圳开学考)如图所示,质
量 M=3 kg 的木块套在固定的水平杆上,并用轻绳与小球相连.
今用与水平方向成 60°角的力 F 拉着小球并带动木块一起向右匀
速运动,F=
N,运动过程中木块与小球的相对位置保持不
变,轻绳与杆的夹角为 30°,g 取 10 m/s2,则( )
A.小球的质量 m=1 kg
,C 错误,D 正确.
解析:对小球受力分析,由平衡条件可知,水平方向上有
Fcos 60°=FTcos 30°,竖直方向上有Fsin 60°=FTsin 30°+mg,
联立解得m=1 kg,A正确,B错误;以小球和木块整体为研究对象,
水平方向上有 Fcos 60°-μFN=0,竖直方向上有 FN+Fsin 60°-
Mg-mg=0,联立解得μ=
答案:AD
【触类旁通1】(2024 年广东汕头二模)扑克牌可以用来“搭房
子”,如图甲所示.每一张纸牌的质量为 m,在图乙的示意图中,
下列说法正确的是(
)
甲
乙
A.a 纸牌受到其他纸牌的作用力大小为 mg,方向竖直向上
B.b 纸牌受到其他纸牌的作用力大小为 mg,方向竖直向上
C.纸牌对地面的压力大小为 6mg
D.每一张纸牌的合外力都不相同
解析:a 纸牌处于静止状态,受到其他纸牌的作用力和自身重
力,根据力的平衡条件可知其他纸牌对 a 纸牌的作用力大小为 mg,
方向竖直向上,A 正确;b 纸牌处于静止状态,受到其他纸牌的作
用力、自身重力和摩擦力作用,则其他纸牌对 b 纸牌的作用力大
小不等于 mg,B 错误;共有 7 张纸牌,整体受力分析,可知地面
对其支持力为 7mg,则纸牌对地面的压力大小为 7mg,C 错误;
每张纸牌都处于静止状态,合外力都为 0,D 错误.
答案:A
平衡中的对称问题
在平衡问题中,尤其是涉及定滑轮和动滑轮的平衡问题中,
以及与活结有关的问题中,往往会出现两条绳子的力大小相等、
角度对称的问题.此情况下,两条绳子上的拉力大小相等,方向关
于角平分线对称.有的题目,我们可以根据对称,判断出这两个力
大小相等,还有的题目,可以根据两个力大小相等,判断出其具
有对称性.
【典题 9】(多选)如图,一光滑的轻滑轮用细绳 OO′悬挂
于 O 点;另一细绳跨过滑轮,其一端悬挂物块 a,另一端系一
位于水平粗糙桌面上的物块 b.外力 F 向右上方拉 b,整个系统处
于静止状态.若 F 方向不变,大小在一定范围内变化,物块 b 仍始
终保持静止,则(
)
A.绳 OO′的张力也在一定范围内变化
B.物块 b 所受到的支持力也在一定范围内变化
C.连接 a 和 b 的绳的张力也在一定范围内变化
D.物块 b 与桌面间的摩擦力也在一定范围内变化
答案:BD
【触类旁通 2】如图所示,在粗糙的水平面上,固定一个半径
为 R 的半圆柱体 M,挡板 PQ 固定在半圆柱体 M 上,挡板 PQ 的延
长线过半圆柱截面圆心 O,且与水平面成 30°角.在 M 和 PQ 之间有
一个质量为 m 的光滑均匀球体 N,其半径也为 R.整个装置处于静止状
态,则下列说法正确的是(
)
A.N 对 PQ 的压力大小为 mg
C.N 对 M 的压力大小为 mg
解析:对球 N 受力分析如图所示,设 N对M
的压力为 F1,N 对 PQ 的压力为 F2,由几何关系
可知,F1 和 F2 与 G 的夹角相等,均为 30°,则
答案:D
平衡中的临界与极值问题
1.临界、极值问题特征.
(1)临界问题:当某物理量变化时,会引起其他几个物理量的
变化,从而使物体所处的平衡状态“恰好出现”或“恰好不出现”,
在问题的描述中常用“刚好”“刚能”“恰好”等语言叙述.
(2)极值问题:平衡物体的极值,一般指在力的变化过程中的
最大值和最小值问题.
极限
分析法 正确进行受力分析和变化过程分析,找到平衡的临界点和
极值点;临界条件必须在变化中寻找,不能在一个状态上
研究临界问题,要把某个物理量推向极大或极小
数学
分析法 通过对问题分析,根据平衡条件列出物理量之间的函数关
系(画出函数图像),用数学方法求极值(如求二次函数极
值、公式极值、三角函数极值)
图解法 根据平衡条件,作出力的矢量图,通过对物理过程的分析,
利用平行四边形定则进行动态分析,确定最大值和最小值
2.解决极值和临界问题的三种方法.
模型一 极限分析法
【典题 10】课堂上,老师准备了“ ”形光滑木板和三个完
全相同、外表面光滑的匀质圆柱形积木,要将三个积木按图所
示(截面图)方式堆放在木板上,则木板与水平面夹角θ的最大值
为(
)
A.30°
B.45°
C.60°
D.90°
解析:θ取 0°时,下面两圆柱之间将会分开,无法稳定,应适
当增大θ以保持系统稳定,此时下面两圆柱之间有弹力.当下面两圆
柱之间的弹力恰好为 0 时,对应的θ为最小值.继续增大θ,右圆柱
和上圆柱之间弹力减小,若θ太大,此两圆柱将分开,当上圆柱和
右圆柱之间的弹力恰好为 0,对应的θ为最大值.临界情况为θmax 时,
左边两圆柱的圆心连线在竖直方向上,保证上圆柱只受到两个力
的作用恰好处于平衡状态,此时上圆柱与右圆柱间相互接触且无
弹力,可得θ=30°,A 正确.
答案:A
模型二 数学分析法
【典题 11】(多选)如图所示,质量为 M 的木楔倾角为θ,在
水平面上保持静止.当将一质量为 m 的木块放在斜面上时正好匀速
下滑,如果用与斜面成α角的力 F 拉着木块沿斜面匀速上滑.重力
加速度为 g,下列说法中正确的是( )
A.当α=2θ时,F 有最小值
B.F 的最小值为 mgsin 2θ
C.在木块匀速上滑过程中,地面对 M 的静摩擦力方向水平
向右
D.在木块匀速上滑过程中,地面对 M 的静摩擦力方向水平
向左
解析:选木块为研究对象,当没加外力 F 时正好匀速下滑,
设木块与斜面间的动摩擦因数为μ ,此时平行于斜面方向必有
mgsin θ=μmgcos θ.当加上外力 F 时,对木块受力分析如图,则
有 Ff=μFN,平行于斜面方向有 Ff+mgsin θ=Fcos α,垂直于斜
A 错误,B 正确;选 M 和 m 组成的整体为研究对象,设水平面
对木楔 M 的摩擦力是Ff′,水平方向受力平衡,则有 Ff′=Fcos(θ+α),
可知摩擦力的方向水平向左,C 错误,D 正确.
答案:BD
模型三 图解法
【典题 12 】(2022 年广东深圳模拟)如图
将光滑的重球放在斜面上,被竖直的挡板挡
住而静止,设球对斜面的压力为 N1,对挡板
的压力为N2,当挡板从竖直缓慢地转到水平位
置的过程中(
)
A.N1 变小,N2 变大
C.N1 变小,N2 先变小后变大
B.N1 变大,N2 变小
D.N1 和 N2 都变小
解析:以球为研究对象,受力分析如图 所示.
答案:C
小球受到重力G、斜面的支持力N1′和挡板的支持力N2′,N1′与N1是作用力和反作用力,大小相等,方向相反,N2′与N2是作用力和反作用力,大小相等,方向相反,由平衡条件得知,N1′和N2′的合力与重力G大小相等、方向相反,作出多个位置N1′和N2′的合力,如图,由图看出,N1′逐渐减小,N2′先减小后增大,当N1′和N2′垂直时,N2′最小,根据牛顿第三定律得知,N1逐渐减小,N2先变小后变大,C正确.
易错分析
挡板从竖直缓慢地转到水平位置的过程分为两个
阶段,第一阶段,挡板从竖直缓慢地转到与斜面垂直,第二阶段,
挡板从与斜面垂直转到水平,挡板对球的弹力存在一个转折点,
图解法中体现为垂直.
第3节
受力分析
共点力的平衡
一、受力分析
受力
1.定义:把指定物体(或研究对象)在特定的物理环境中受到的
所有外力都分析出来,并画出物体____________的示意图的过程.
2.受力分析步骤.
(1)选取对象:研究对象可以是质点、结点、某个物体,或几
个物体组成的系统.原则上使问题的研究处理尽量简便.
(2)按顺序找力:先把研究对象从周围环境中隔离出来,再按
照性质力的顺序逐一分析:先分析________(重力、电场力、磁场
力),再分析__________(弹力、摩擦力),最后分析其他力.
(3)画出受力示意图:把物体所受的力一一画在受力图上,并
标明各力的方向,注意不要将施出的力画在图上.
(4)检验:防止错画、漏画、多画力.
场力
接触力
特别提醒:弹力、摩擦力的产生条件之一都是接触,因此在
分析这两种力时先找接触面,在每个接触面上逐一分析这两种力.
二、共点力的平衡
1.平衡状态.
物体处于______状态或________________状态.
2.平衡条件.
静止
匀速直线运动
如图甲所示,小球静止不动,则小球 F合=0;如图乙所示,
物块做匀速直线运动,则物块 Fx=0,Fy=0.
甲
乙
3.平衡条件的推论.
相等
相反
三角形
(1)二力平衡:如果物体在两个共点力的作用下处于平衡状态,
这两个力必定大小相等,方向相反.
(2)三力平衡:物体在三个共点力的作用下处于平衡状态,其
中任何一个力与另外两个力的合力大小______,方向______,并
且这三个力的矢量可以形成一个封闭的矢量__________.
(3)多力平衡:物体在多个共点力的作用下处于平衡状态,其
中任何一个力与另外几个力的合力大小______,方向______.
相等
相反
【基础自测】
1.判断下列题目的正误.
(1)物体的速度为零即处于平衡状态.(
)
(2)物体处于平衡状态时,其加速度一定为零.(
)
(3)物体受两个力作用处于平衡状态,这两个力必定等大反向.
(
(
)
(4) 物体处于平衡状态时,其所受的作用力必定为共点力.
)
(5)物体受三个力 F1、F2、F3 作用处于平衡状态,若将 F2 转动
)
90°,则三个力的合力大小为 F2.(
答案:(1)× (2)√ (3)√ (4)× (5)√
2.如图所示,某物体在四个共点力作用下处于平衡状态,若
将F4=5 N 的力沿逆时针方向转动 90°,其余三个力的大小和方
)
向都不变,则此时物体所受合力的大小为(
答案:C
3.如图所示,利用三根等长的轻绳以正三棱锥形将花盆竖直
悬空吊在挂钩上,下列说法正确的是( )
A.三根轻绳对花盆作用力的合力方向一定竖直向上
B.每根轻绳的拉力均为花盆重力大小的三分之一
C.若将三根轻绳缩短相同的长度,则每根轻绳的拉
力减小
D.若将三根轻绳增加相同的长度,则三根轻绳对花
盆作用力的合力增大
解析:花盆处于静止状态,由平衡条件可知,三根轻绳对花
盆作用力的合力大小等于花盆的重力大小,方向与重力的方向相
反,即竖直向上,A 正确,D 错误;设花盆的重力为 G,每根轻绳
中的拉力为 F,轻绳与竖直方向的夹角均为θ,则G=3Fcos θ,解
答案:A
4.(2022 年广东湛江模拟)如图所示,一只蚂蚁沿着向下弯成
弧面的树叶从 A 经 B 缓慢爬到 C 的过程中,下列说法正确的
是(
)
A.树枝对蚂蚁的作用力先增大后减小
B.树枝对蚂蚁的作用力先减小后增大
C.树枝对蚂蚁的摩擦力先减小后增大
D.树枝对蚂蚁的摩擦力先增大后减小
解析:树枝对蚂蚁的作用力即是树枝对蚂蚁的支持力和摩擦
力的合力,与蚂蚁的重力是一对平衡力,由于重力总竖直向下,
故这个合力也竖直向上,大小不变,AB 错误;缓慢相当于动态
平衡,设摩擦力与水平方向夹角为θ,有 f=mgsin θ,从 A 到 B,
随着θ的减小,摩擦力先减小.从 B 到 C,随着θ的增大,摩擦力再
增大,C 正确,D 错误.
答案:C
热点1 受力分析
【典题1】(多选,2024 年广东梅州期中)如图,质量均为 m
的 A、B、C 三个木块叠放在粗糙的水平地面上,A、B 接触面沿
)
水平方向,整个系统处于静止状态,下列说法正确的是(
A.A 对 B 压力的大小等于 mg
B.木块 B 受到 4 个力的作用
C.地面对 C 的摩擦力水平向左
D.地面对 C 的支持力等于 3mg
解析:对 A 受力分析可知,B 对 A 的支持力大小等于 mg,则
由牛顿第三定律可知,A 对 B 压力的大小等于 mg,A 正确;木块
B 受到重力、斜面的支持力和摩擦力以及 A 对 B 的压力共 4 个力
的作用,B 正确;对 ABC 整体分析可知,水平方向受力平衡,则
地面对 C 无摩擦力作用,竖直方向平衡可知,地面对 C 的支持力
等于 3mg,C 错误,D 正确.
答案:ABD
条件
判据 不同性质的力产生条件不同,进行受力分析时最基本的判据是根据其产生条件
效果
判据 有时候是否满足某力产生的条件是很难判定的,可先根据物体的运动状态进行
分析,再运用平衡条件或牛顿运动定律判定未知力,也可应用“假设法”.
(1)物体平衡时合外力必定为零.
(2)物体做变速运动时必定合力方向沿加速度方向,合力大小满足 F=ma.
(3)物体做匀速圆周运动时必定合外力大小恒定,满足 F= ,方向始终指向
圆心
特征
判据 在有些受力情况较为复杂的情况下,我们根据力产生的条件及其作用效果仍不
能判定该力是否存在时,可从力的作用是相互的这个基本特征出发,通过判定
其反作用力是否存在来判定该力
方法技巧 受力分析的三个常用判据
方法 基本思路 求解方法 条件
正交
分解法 变矢量运算为代数运算 将各力分解到x轴和y轴上,运用两坐标轴上的合力等于零的条件列方程求解,即∑Fx=0,∑Fy=0 三个或三个以上共点力作用下物体的平衡
热点 2 静态平衡
[热点归纳]
处理平衡问题的常用方法.
方法 基本思路 求解方法 条件
力的
合成法 通过平行四边形定则,构建矢量三角形,利用几何知识求解 物体受到三个力平衡时,任意两个力的合力与第三个力等大、反向,可以应用三角函数、相似三角形等知识求解 三力平衡
(续表)
考向 1 合成法
【典题2】(2023 年河北卷)如图,轻质细杆 AB 上穿有一个质
量为 m 的小球 C,将杆水平置于相互垂直的
固定光滑斜面上,系统恰好处于平衡状态.已
知左侧斜面与水平面成 30°角,则左侧斜面
对杆 AB 支持力的大小为(
)
答案:B
思路导引
本题与常见题目的区别是有一根轻杆,可以“无
视”杆的存在,球在重力和两个弹力的作用下处于平衡状态,弹
力的方向与斜面垂直,先找出两个弹力作用线的交点,此交点确
定“重心”的位置,然后应用三力平衡求解.
考向 2 正交分解法
【典题 3】(2022 年辽宁卷)如图所示,蜘蛛用蛛丝将其自身
悬挂在水管上,并处于静止状态.蛛丝 OM、ON 与竖直方向夹角
)
分别为α、β(α>β).用 F1、F2 分别表示 OM、ON 的拉力,则(
A.F1 的竖直分力大于 F2 的竖直分力
B.F1 的竖直分力等于 F2 的竖直分力
C.F1 的水平分力大于 F2 的水平分力
D.F1 的水平分力等于 F2 的水平分力
解析:对结点 O 受力分析可得,水平方向 F1sin α=F2sin β,
即 F1 的水平分力等于 F2 的水平分力,C 错误,D 正确;对结点
O受力分析可得,竖直方向 F1cos α+F2cos β=mg,解得 F1=
答案:D
思路导引 蛛丝 OM、ON 与竖直方向夹角分别为α、β不相
等,两角之和也不为直角,力按效果分解不适应,只能采用正交
分解的方法,将结点受的力在水平方向和竖直方向正交分解.
热点 3 共点力作用下的动态平衡
[热点归纳]
1.动态平衡:通过控制某些物理量,使物体的状态发生缓慢的
变化,而在这个过程中物体又始终处于一系列的平衡状态,在问
题的描述中常用“缓慢”等语言叙述.
图解法 对研究对象在动态变化过程中的若干状态进行受力分析,在
同一图中作出物体在若干状态下所受的力的平行四边形(或
三角形),即为图解法.此法常用于求解三力平衡且有一个力
是恒力、另有一个力方向不变的问题
相似三
角形法 物体在三力作用下动态平衡,且其中一个力的大小和方向恒
定,其他两个力的大小和方向都可变,这些变化是由物体间
距离的变化引起的,且题目还给出了有关边的长度,这时要
注意力的矢量三角形和几何三角形相似的知识运用
2.分析动态平衡问题的常用方法.
解析法 对研究对象进行受力分析,先画出受力示意图,再根据物体
的平衡条件列式求解,得到因变量与自变量的一般函数表达
式,最后根据自变量的变化确定因变量的变化
正弦
定理法 物体受到三个力的作用,其中的一个力大小、方向都不变,
另外两个力的方向都发生变化,但之间的夹角保持不变,可
利用正弦定理法分析
(续表)
3.基本思路:化“动”为“静”,“静”中求“动”.
考向 1 图解法
【典题 4】(2024 年广东佛山二模)如图,用 AB 与 AC 两根绳
悬挂一质量分布不均(重心偏左)的矩形画框,画框底部需保持与水
平地面平行.若保持 AB绳长不变,将 C 端左移,AC 绳缩短至某一
长度(但 AC 绳仍长于 AB 绳)后悬挂画框,画框保持原状态不动,
则改变 AC 绳长前后(
)
A.AB 绳的拉力大小总等于 AC 绳的拉力大小
B.AB 绳的拉力大小总小于 AC 绳的拉力大小
C.AB 绳的拉力大小不变
D.AC 绳的拉力大小可能相等
解析:对画框受力分析,如图甲所示.
甲
设 AB 绳上的拉力与水平方向的夹角为θ1,AC 绳上的拉力与
水平方向的夹角为θ,根据题意,保持 AB 绳长不变,将 C 端左移,
AC 绳缩短至某一长度(但 AC 绳仍长于 AB 绳),则可知该过程中θ1
始终不变,且根据几何关系,始终有θ1>θ2,则在水平方向根据平
衡条件有
乙
FABcos θ1=FACcos θ2,由于θ1始终大于θ2,因此FAB始终大于FAC,AB错误;重力为恒力,AB绳上力的方向始终不变,做出力的矢量三角形如图乙所示.
可知,随着 AC 绳将 C 端向左移动,绳 AC 与竖直方向的夹角
在减小,该过程中绳 AC 上的拉力可能先减小后增大,当绳 AC 垂
直于绳 AB 时,绳 AC 上的拉力有最小值,因此 AC 绳的拉力大小
可能相等,该过程中绳 AB 上的拉力 FAB 逐渐减小,但始终大于绳
AC 上的拉力 FAC,C 错误,D 正确.
答案:D
考向 2 相似三角形法
【典题5】(2024年广东深圳一模)如图所示,用一轻绳通过定
滑轮将质量为 m 的小球静置在光滑的半圆柱体上,小球的半径远
小于半圆柱体截面的半径 R,绳 AB 长度为 L,长度为 H 的杆 BC
竖直且与半圆柱体边缘相切,OA 与水平面夹角为θ,不计一切摩
擦,重力加速度为 g,下列表达式表示绳对小球的拉力 F 是(
)
A.
mgL
H
B.
mgR(1+cos θ)
(H+Rtan θ)cos θ
C.
mgL
H+Rtan θ
D.
mgLtan θ
Htan θ+R
解析:根据题意,对小球受力分析,受拉力、支持力和重力,
把拉力和支持力平移,组成矢量三角形,延长 AO 和 BC 交于 D
点,如图所示.
答案:C
思路导引
应用力的三角形与几何三角形相似,长度不变的
边对应大小不变的力,长度变化的边对应大小变化的力,即力与
对应边同趋势变化.
考向 3 解析法
【典题6】(2024 年广东惠州质检)运动会比赛结束后,教师为
参赛的运动员颁奖,我们可以把奖牌简化为一根质量不计的轻绳
和位于轻绳中点质量为 m 的重物,重物可视为质点.教师手抓在轻
绳的两端,重力加速度为 g,下列说法正确的是(
)
A.当轻绳夹角变大时,绳的张力减小
B.轻绳夹角不变,教师用力抓轻绳时,轻绳与教师手之间摩
擦力增加
D.教师双手对轻绳的作用力方向为沿绳斜向上
解析:根据题意,对小球受力分析,由平衡条件有 2Fcos θ=
变小,轻绳上拉力大小变大,轻绳夹角不变,轻绳上拉力大小不
变,由平衡条件可知,教师用力抓轻绳时,轻绳与教师手之间摩
擦力不变,AB 错误,C正确;根据题意,把轻绳和小球看做整体,
对整体受力分析,由平衡条件可知,教师双手对轻绳的作用力与
小球的重力等大反向,则教师双手对轻绳的作用力方向为竖直向
上,D 错误.
答案:C
考向 4 正弦定理法
【典题 7】(2022 年河北卷)如图,用两根等长的细绳将
一匀质圆柱体悬挂在竖直木板的 P 点,将木板以
底边 MN 为轴向后方缓慢转动直至水平,绳与木
板之间的夹角保持不变,忽略圆柱体与木板之间
的摩擦,在转动过程中(
)
A.圆柱体对木板的压力逐渐增大
B.圆柱体对木板的压力先增大后减小
C.两根细绳上的拉力均先增大后减小
D.两根细绳对圆柱体拉力的合力保持不变
解析:设两绳子对圆柱体的拉力的合力为 T,木板对圆柱体的
支持力为 N,绳子与木板夹角为 β,从右向左看如图 所示.
在矢量三角形中,根据正弦定理
在木板以直线 MN 为轴向后方缓慢转动直至水平过程中,α不
变,γ 从 90°逐渐减小到 0,又 γ+β+α=180°,且 α<90°,可
知 90°<γ+β<180°,则 0<β<180°,
sin γ不断减小,可知 T 不断减小,sin β先增大后减小,可知 N 先
增大后减小,结合牛顿第三定律可知,圆柱体对木板的压力先增
大后减小,设两绳子之间的夹角为 2θ,绳子拉力为 T′,则2T′cos θ
T
2cos θ
,θ 不变,T 逐渐减小,可知绳子拉力不断减
=T 可得 T′=
小,B 正确.
答案:B
思路导引
将两根细绳的拉力看作一个力,这样圆柱体在三
个力作用下平衡,构建力的三角形:拉力、重力、挡板的弹力。
确定该三角形中角度是否变化及变化特点:绳与木板之间的夹角
保持不变,挡板弹力与竖直方向间的夹角从 90°逐渐减小到 0,另
外一个角根据三角形内角和 180°得到,然后应用正弦定理判断力
的变化情况.
整体法与隔离法的应用
当物理情境中涉及物体较多时,就要考虑采用整体法和隔离
法.
同时满足上述两个条件即可采用整体法.
必须将物体从系统中隔离出来,单独地进行受力分析,列出
方程.
(3)整体法和隔离法的交替运用
对于一些复杂问题,比如连接体问题,通常需要多次选用研
究对象,这样整体法和隔离法要交替使用.
【典题 8】(多选,2023 年广东深圳开学考)如图所示,质
量 M=3 kg 的木块套在固定的水平杆上,并用轻绳与小球相连.
今用与水平方向成 60°角的力 F 拉着小球并带动木块一起向右匀
速运动,F=
N,运动过程中木块与小球的相对位置保持不
变,轻绳与杆的夹角为 30°,g 取 10 m/s2,则( )
A.小球的质量 m=1 kg
,C 错误,D 正确.
解析:对小球受力分析,由平衡条件可知,水平方向上有
Fcos 60°=FTcos 30°,竖直方向上有Fsin 60°=FTsin 30°+mg,
联立解得m=1 kg,A正确,B错误;以小球和木块整体为研究对象,
水平方向上有 Fcos 60°-μFN=0,竖直方向上有 FN+Fsin 60°-
Mg-mg=0,联立解得μ=
答案:AD
【触类旁通1】(2024 年广东汕头二模)扑克牌可以用来“搭房
子”,如图甲所示.每一张纸牌的质量为 m,在图乙的示意图中,
下列说法正确的是(
)
甲
乙
A.a 纸牌受到其他纸牌的作用力大小为 mg,方向竖直向上
B.b 纸牌受到其他纸牌的作用力大小为 mg,方向竖直向上
C.纸牌对地面的压力大小为 6mg
D.每一张纸牌的合外力都不相同
解析:a 纸牌处于静止状态,受到其他纸牌的作用力和自身重
力,根据力的平衡条件可知其他纸牌对 a 纸牌的作用力大小为 mg,
方向竖直向上,A 正确;b 纸牌处于静止状态,受到其他纸牌的作
用力、自身重力和摩擦力作用,则其他纸牌对 b 纸牌的作用力大
小不等于 mg,B 错误;共有 7 张纸牌,整体受力分析,可知地面
对其支持力为 7mg,则纸牌对地面的压力大小为 7mg,C 错误;
每张纸牌都处于静止状态,合外力都为 0,D 错误.
答案:A
平衡中的对称问题
在平衡问题中,尤其是涉及定滑轮和动滑轮的平衡问题中,
以及与活结有关的问题中,往往会出现两条绳子的力大小相等、
角度对称的问题.此情况下,两条绳子上的拉力大小相等,方向关
于角平分线对称.有的题目,我们可以根据对称,判断出这两个力
大小相等,还有的题目,可以根据两个力大小相等,判断出其具
有对称性.
【典题 9】(多选)如图,一光滑的轻滑轮用细绳 OO′悬挂
于 O 点;另一细绳跨过滑轮,其一端悬挂物块 a,另一端系一
位于水平粗糙桌面上的物块 b.外力 F 向右上方拉 b,整个系统处
于静止状态.若 F 方向不变,大小在一定范围内变化,物块 b 仍始
终保持静止,则(
)
A.绳 OO′的张力也在一定范围内变化
B.物块 b 所受到的支持力也在一定范围内变化
C.连接 a 和 b 的绳的张力也在一定范围内变化
D.物块 b 与桌面间的摩擦力也在一定范围内变化
答案:BD
【触类旁通 2】如图所示,在粗糙的水平面上,固定一个半径
为 R 的半圆柱体 M,挡板 PQ 固定在半圆柱体 M 上,挡板 PQ 的延
长线过半圆柱截面圆心 O,且与水平面成 30°角.在 M 和 PQ 之间有
一个质量为 m 的光滑均匀球体 N,其半径也为 R.整个装置处于静止状
态,则下列说法正确的是(
)
A.N 对 PQ 的压力大小为 mg
C.N 对 M 的压力大小为 mg
解析:对球 N 受力分析如图所示,设 N对M
的压力为 F1,N 对 PQ 的压力为 F2,由几何关系
可知,F1 和 F2 与 G 的夹角相等,均为 30°,则
答案:D
平衡中的临界与极值问题
1.临界、极值问题特征.
(1)临界问题:当某物理量变化时,会引起其他几个物理量的
变化,从而使物体所处的平衡状态“恰好出现”或“恰好不出现”,
在问题的描述中常用“刚好”“刚能”“恰好”等语言叙述.
(2)极值问题:平衡物体的极值,一般指在力的变化过程中的
最大值和最小值问题.
极限
分析法 正确进行受力分析和变化过程分析,找到平衡的临界点和
极值点;临界条件必须在变化中寻找,不能在一个状态上
研究临界问题,要把某个物理量推向极大或极小
数学
分析法 通过对问题分析,根据平衡条件列出物理量之间的函数关
系(画出函数图像),用数学方法求极值(如求二次函数极
值、公式极值、三角函数极值)
图解法 根据平衡条件,作出力的矢量图,通过对物理过程的分析,
利用平行四边形定则进行动态分析,确定最大值和最小值
2.解决极值和临界问题的三种方法.
模型一 极限分析法
【典题 10】课堂上,老师准备了“ ”形光滑木板和三个完
全相同、外表面光滑的匀质圆柱形积木,要将三个积木按图所
示(截面图)方式堆放在木板上,则木板与水平面夹角θ的最大值
为(
)
A.30°
B.45°
C.60°
D.90°
解析:θ取 0°时,下面两圆柱之间将会分开,无法稳定,应适
当增大θ以保持系统稳定,此时下面两圆柱之间有弹力.当下面两圆
柱之间的弹力恰好为 0 时,对应的θ为最小值.继续增大θ,右圆柱
和上圆柱之间弹力减小,若θ太大,此两圆柱将分开,当上圆柱和
右圆柱之间的弹力恰好为 0,对应的θ为最大值.临界情况为θmax 时,
左边两圆柱的圆心连线在竖直方向上,保证上圆柱只受到两个力
的作用恰好处于平衡状态,此时上圆柱与右圆柱间相互接触且无
弹力,可得θ=30°,A 正确.
答案:A
模型二 数学分析法
【典题 11】(多选)如图所示,质量为 M 的木楔倾角为θ,在
水平面上保持静止.当将一质量为 m 的木块放在斜面上时正好匀速
下滑,如果用与斜面成α角的力 F 拉着木块沿斜面匀速上滑.重力
加速度为 g,下列说法中正确的是( )
A.当α=2θ时,F 有最小值
B.F 的最小值为 mgsin 2θ
C.在木块匀速上滑过程中,地面对 M 的静摩擦力方向水平
向右
D.在木块匀速上滑过程中,地面对 M 的静摩擦力方向水平
向左
解析:选木块为研究对象,当没加外力 F 时正好匀速下滑,
设木块与斜面间的动摩擦因数为μ ,此时平行于斜面方向必有
mgsin θ=μmgcos θ.当加上外力 F 时,对木块受力分析如图,则
有 Ff=μFN,平行于斜面方向有 Ff+mgsin θ=Fcos α,垂直于斜
A 错误,B 正确;选 M 和 m 组成的整体为研究对象,设水平面
对木楔 M 的摩擦力是Ff′,水平方向受力平衡,则有 Ff′=Fcos(θ+α),
可知摩擦力的方向水平向左,C 错误,D 正确.
答案:BD
模型三 图解法
【典题 12 】(2022 年广东深圳模拟)如图
将光滑的重球放在斜面上,被竖直的挡板挡
住而静止,设球对斜面的压力为 N1,对挡板
的压力为N2,当挡板从竖直缓慢地转到水平位
置的过程中(
)
A.N1 变小,N2 变大
C.N1 变小,N2 先变小后变大
B.N1 变大,N2 变小
D.N1 和 N2 都变小
解析:以球为研究对象,受力分析如图 所示.
答案:C
小球受到重力G、斜面的支持力N1′和挡板的支持力N2′,N1′与N1是作用力和反作用力,大小相等,方向相反,N2′与N2是作用力和反作用力,大小相等,方向相反,由平衡条件得知,N1′和N2′的合力与重力G大小相等、方向相反,作出多个位置N1′和N2′的合力,如图,由图看出,N1′逐渐减小,N2′先减小后增大,当N1′和N2′垂直时,N2′最小,根据牛顿第三定律得知,N1逐渐减小,N2先变小后变大,C正确.
易错分析
挡板从竖直缓慢地转到水平位置的过程分为两个
阶段,第一阶段,挡板从竖直缓慢地转到与斜面垂直,第二阶段,
挡板从与斜面垂直转到水平,挡板对球的弹力存在一个转折点,
图解法中体现为垂直.
同课章节目录
