2025秋高考物理复习第二章第2节力的合成与分解课件
文档属性
| 名称 | 2025秋高考物理复习第二章第2节力的合成与分解课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-05 17:39:30 | ||
图片预览











文档简介
(共58张PPT)
第2节
力的合成与分解
一、力的合成
1.合力与分力.
合
分
等效替代
合成
(1)定义:如果一个力单独作用的效果与几个力同时作用的共
同效果相同,这个力就叫那几个力的________力,而那几个力就
叫这个力的________力.
(2)关系:合力与分力之间在效果上是____________的关系.
(3)力的合成与分解:求几个力的合力的过程叫力的________,
求一个力的分力的过程叫力的分解.
2.平行四边形定则.
对角线
大小
(1)平行四边形定则:求两个互成角度的共点力 F1、F2 的合力,
可以用表示 F1、F2 的有向线段为边作平行四边形,平行四边形的
__________(在两个有向线段 F1、F2 之间)就表示合力的________
和方向,如图甲所示.
(2)三角形定则:求两个互成角度的共点力 F1、F2 的合力,可
以把表示 F1、F2 的线段________顺次相接地画出,把 F1、F2 的另
外两端连接起来,则此连线就表示______的大小和方向,如图乙
所示.
首尾
合力
特别提醒:(1)两个分力一定时,夹角θ越大,合力越小.
(2)合力一定时,两等大分力的夹角θ越大,两分力越大.
(3)合力可以大于分力,等于分力,也可以小于分力.
二、力的分解
分力
平行四边形
1.概念:求一个力的________的过程.
2.遵循的原则:______________定则或三角形定则.
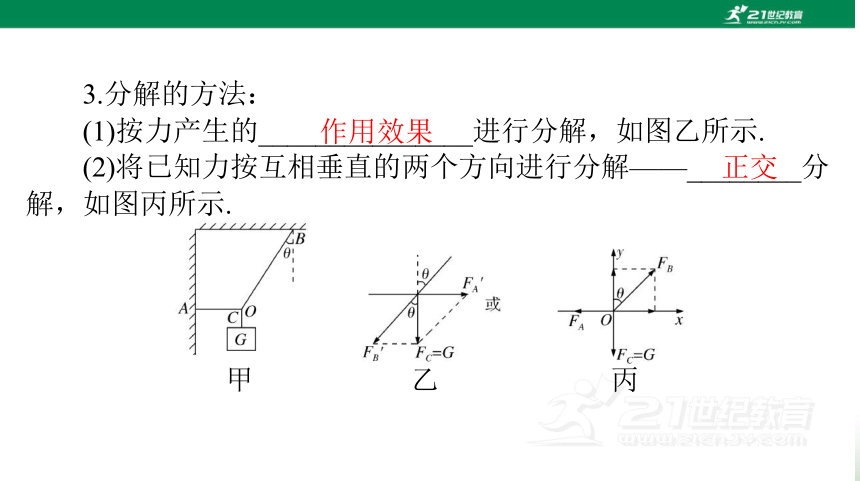
3.分解的方法:
作用效果
正交
(1)按力产生的_______________进行分解,如图乙所示.
(2)将已知力按互相垂直的两个方向进行分解——________分
解,如图丙所示.
甲
丙
乙
【基础自测】
1.判断下列题目的正误.
(1)合力及其分力可以同时作用在物体上.(
)
(2)几个力的共同作用效果可以用一个力来代替.(
)
(3)两个力的合力一定比其分力大.(
)
(4)互成角度(非 0°或 180°)的两个力的合力与分力间一定构
成封闭的三角形.(
)
(5)两分力大小一定,夹角越小,合力越大.(
)
答案:(1)× (2)√ (3)× (4)√ (5)√
2.如图所示,F1、F2、F3 三个力恰好构成封闭的直角三角形,
则这三个力的合力大小为( )
A.0
B.2F1
C.2F2
D.2F3
解析:由矢量合成的法则可知,F1 与 F3 的合力为 F2,则这三
个力的合力大小为 2F2,选 C.
答案:C
)
3.关于力的合成与分解,下列说法正确的是(
A.合力一定大于任意一个分力
B.合力、分力大小是可以全部相等的
C.分力、合力一定不能都在一条直线上
D.合力大小不可能等于两个分力中的任何一个
答案:B
4.已知竖直平面内有一个大小为 10 N 的力作用于 O 点,该力
与x 轴正方向之间的夹角为30°,与 y 轴正方向之间的夹角为60°,
)
现将它分解到 x 轴和 y 轴方向上,则(
解析:画出坐标及受力情况,如图所示,已知两分力方向,
Fsin 30°=5 N.
答案:B
热点 1 力的合成
[热点归纳]
1.两个共点力的合力范围.
|F1-F2|≤F≤F1+F2.
2.重要结论.
(1)两个分力一定时,夹角θ越大,合力越小.
(2)合力一定时,两等大分力夹角θ越大,两分力越大.
(3)合力可以大于分力,等于分力,也可以小于分力.
3.力合成的方法.
(1)作图法.
(2)计算法.
若两个力 F1、F2 的夹角为θ,如图所示,
合力的大小可由余弦定理得到:
4.三个共点力的合成.
(1)最大值:三个力共线且同向时,其合力最大,为 F1+F2+
F3.
(2)最小值:任取两个力,求出其合力的范围,如果第三个力
在这个范围之内,则三个力的合力的最小值为零.如果第三个力不
在这个范围内,则合力的最小值为最大的一个力减去另外两个较
小的力的大小之和.
5.几种特殊情况的共点力的合成.
【典题 1】(2023 年广东广州二模)耙在中国已有 1500 年以
上的历史,北魏贾思勰所著的《齐民要术》中称之为“铁齿楱”,
将使用此农具的作业称作耙.如图甲所示,牛通过两根耙索拉耙
沿水平方向匀速耙地.两根耙索等长且对称,延长线的交点为O1,
夹角∠AO1B=60°,拉力大小均为 F,平面 AO1B 与水平面的
夹角为 30°(O2 为 AB 的中点),如图乙所示.忽略耙索质量,下
列说法正确的是(
)
乙
甲
A.两根耙索的合力大小为 F
答案:B
思路导引
三个力合力的最大值为三者之和,最小值分两种
情况讨论:若三力能构成三角形,合力最小值为 0;若不能构成三
角形,最小值为最大的力减去另外两个力所得的差.分析 C、D 选
项时,可参照上述思路.
【迁移拓展1】(2024 年广东广州模拟)如图所示俯视图,当汽
车陷入泥潭时,需要救援车辆将受困车辆拖拽驶离.救援人员发现
在受困车辆的前方有一坚固的树桩可以利用,根据你所学过的知
识判断,下列情况中,救援车辆用同样的力拖拽,受困车辆受到
的拉力最大的方案为(
)
A
B
C
D
解析:A 图中,根据受力分析可知,救援车辆的拉力为受困
车辆所受拖拽力的一半;B 图中,根据受力分析可知,救援车辆
的拉力为缆绳两侧拖拽拉力的合力,因初始时刻两分力夹角接近
180°,合力远小于两分力(小于所受拖拽力的一半);C图中,缆绳
与树桩构成定滑轮系统,仅改变力的方向,未改变力的大;D 图
中,根据受力分析可知,救援车辆的拉力为受困车辆所受拖拽力
的 2 倍;综上所述 B 图最省力,B 正确.
答案:B
热点 2 力的分解
考向 1 力的正交分解法
[热点归纳]
1.定义:将已知力按互相垂直的两个方向进行分解的方法.
2.步骤:如图所示,建立直角坐标系.通常选择共点力的作
用点为坐标原点,建立 x、y 轴让尽可能多的力落在坐标轴上.
3.把不在坐标轴上的各力向坐标轴进行正交分解.
【典题 2】(2021 年广东卷)唐代《耒耜经》记载了曲辕犁相对
直辕犁的优势之一是起土省力,设牛用大小相等的拉力 F 通过耕
索分别拉两种犁,F 与竖直方向的夹角分别为α 和β,α<β,如图
所示,忽略耕索质量,耕地过程中,下列说法正确的是( )
A.耕索对曲辕犁拉力的水平分力比对直辕犁的大
B.耕索对曲辕犁拉力的竖直分力比对直辕犁的大
C.曲辕犁匀速前进时,耕索对犁的拉力小于犁对耕索的拉力
D.直辕犁加速前进时,耕索对犁的拉力大于犁对耕索的拉力
解析:将拉力 F 正交分解如图所示.
则在 x 方向可得出 Fx曲=Fsin α,Fx直=Fsin β,在 y 方向可得
出 Fy曲=Fcos α,Fy直=Fcos β
由题知α<β则 sin αcos β,则可得到 Fx曲Fy曲>Fy直,A 错误,B 正确;耕索对犁的拉力与犁对耕索的拉力是
一对相互作用力,它们大小相等,方向相反,无论是加速还是匀速,
则 CD 错误.
答案:B
实例 分解思路
拉力F可分解为水平分力F1=Fcos α和竖直分力F2=Fsin α
重力分解为使物体沿斜面向下的分力F1=mg sin α和使物体压紧斜面的分力F2=mg cos α
考向 2 力的按效果分解
[热点归纳]
1.常见的按力产生的效果进行分解的情形.
实例 分解思路
重力分解为使球压紧挡板的分力 F1=mg tan α和使球
mg
压紧斜面的分力 F2=
cos α
重力分解为使球压紧竖直墙壁的分力 F1=mg tan α和
mg
使球拉紧悬线的分力 F2=
cos α
(续表)
实例 分解思路
重力分解为使球拉紧 AO 线的分力 F2 和使球拉紧 BO
mg
线的分力 F1,大小 F1=F2=
2sin α
(续表)
2.按实际效果分解力的一般思路.
3.力的分解方法选取原则.
(1)一般来说,当物体受到三个或三个以下的力时,常按实际
效果进行分解,若这三个力中,有两个力互相垂直,优先选用正
交分解法.
(2)当物体受到三个以上的力时,常用正交分解法.
【典题3】(2024 年广东佛山开学考)如图甲所示是斧子砍进木
桩时的情境,其横截面如图乙所示,斧子的剖面可视作顶角为θ的
等腰三角形,当施加竖直向下的力 F 时,则(
)
甲
乙
B.施加的力 F 越小,斧头对木桩的侧向压力越大
C.施加相同的力 F,θ越大的斧子,越容易劈开木桩
D.施加相同的力 F,θ越小的斧子,越容易劈开木桩
解析:将力 F 进行分解,如图所示.
答案:D
思路导引
本题除了应用分解的方法分析外,同样可以应用
合成的方法:两个分力 F1、F2 的合力大小等于 F,结合图中四边
形为菱形的特点,应用几何关系求解.
已知条件 示意图 解的情况
已知合力与两个分力的方向,并且不在一条直线上
有唯一解
考向 3 力的分解中的多解问题
[热点归纳]
已知条件 示意图 解的情况
已知合力与两个分
力的大小 在同一平面内有两解或无解(当F<|F1-F2|或F>F1+F2时无解)
(续表)
已知条件 示意图 解的情况
已知合力与一个分
力的大小和方向
有唯一解
(续表)
已知条件 示意图 解的情况
已知合力与一个分力的大小及另一个分力的方向 在0<θ<90°时有三种情况:
①当F1=F sin θ或F1>F时,有一组解;
②当F1③当F sin θ若90°≤θ≤180°,仅F1>F时有一组解,其余情况无解
(续表)
【典题 4】已知两个共点力 F1、F2 的合力 F 大小为 10 N,力
F1 的大小为 6 N,力 F2 的方向与合力 F 的方向的夹角为θ,则θ的
值可能为(arcsin 0.6=37°)( )
A.30°
B.45°
C.60°
D.90°
2023年广东深圳开学考
解析:以合力 F 的起点为圆心,以表示 6 N 大小为半径作图,
答案:A
如图所示.则连接F的终点和圆上的任意一点均可以得出 F2的大小和方向,当F2与圆相切时得到的夹角最大,由几何定律可知,
是可能的,选项中只有 A 符合,A 正确.
“死结”模型 “活结”模型
“死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点.“死结”两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等 “活结”可理解为把绳子分成两段,且可以沿绳子移动的结点.“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的.绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的平分线
热点 3 绳模型、杆模型
1.轻绳模型.
【典题 5】如图,悬挂甲物体的细线拴牢在一不可伸长的轻
质细绳上 O 点处,绳的一端固定在墙上,另一端通过光滑定滑轮
与物体乙相连.甲、乙两物体质量相等.系统平衡时,O 点两侧绳与
竖直方向的夹角分别为α和β.若α=70°,则β等于( )
A.45°
B.55°
C.60°
D.70°
解析:甲物体是拴牢在 O 点,且甲、乙两物体的质量相等,
则甲、乙绳的拉力大小相等,O 点处于平衡状态,则左侧绳子拉
力的方向在甲、乙绳子的角平分线上,如图所示.根据几何关系
有 180°=2β+α,解得β=55°,故选 B.
答案:B
【迁移拓展 2】如图所示,M、 N 两支架固定在高台边缘,
钢绳两端连接到两个支架上等高的位置,钢绳的长度可通过固定
在支架 M 上的电动机收放.某杂技演员(可视为质点)抓住套在钢绳
上的滑环静止在高空,滑环可沿钢绳无摩擦滑动.则下列说法正确
的是( )
)
A.若启动电动机使钢绳缓慢缩短,钢绳拉力将不断减小
B.若启动电动机使钢绳缓慢缩短,左侧钢绳拉力将增大,右
侧钢绳拉力将减小
C.若启动电动机使钢绳缓慢伸长,钢绳拉力将不断减小
D.若启动电动机使钢绳缓慢伸长,演员运动的轨迹为偏向支
架 N 一侧的曲线
解析:设滑环两侧钢绳与水平面的夹角为θ,对杂技演员由平
衡条件可得 2Tsin θ=mg,若启动电动机使钢绳缓慢缩短,则θ减
小,两侧钢绳拉力将不断增大,若启动电动机使钢绳缓慢伸长,
则θ增大,两侧钢绳拉力将不断减小,C 正确,AB 错误;由于钢
绳两端连接到两个支架上等高的位置,同一条钢绳上拉力大小处
处相等,由对称性可知,滑环两侧钢绳与水平面的夹角总是相等,
故启动电动机使钢绳缓慢伸长,演员运动的轨迹为竖直向下,若
演员运动的轨迹偏向支架 N 一侧,滑环两侧的钢绳与水平面的夹
角就不会相等,D 错误.
答案:C
“动杆”模型 “定杆”模型
对于一端有转轴或有铰链的轻杆,其提供的弹力方向一定是沿着轻杆的方向 一端固定的轻杆(如一端“插入”墙壁或固定于地面),其提供的弹力不一定沿着轻杆的方向,力的方向只能根据具体情况进行受力分析.根据平衡条件或牛顿第二定律确定杆中的弹力的大小和方向
2.轻杆模型.
【典题 6】如图甲所示,轻绳 AD 跨过固定在水平横梁BC 右
端的定滑轮挂住一个质量为10 kg的物体,∠ACB=30°;图乙中轻
杆 HP 一端用铰链固定在竖直墙上,另一端P通过细绳EP拉住,EP
与水平方向也成 30°,轻杆的 P 点用细绳 PQ 拉住一个质量也为
10 kg 的物体.g 取 10 N/kg,求轻绳 AC 段的拉力大小 FAC 与细绳 EP
段的拉力大小 FEP 之比.
甲
乙
解:题图中的两个物体都处于平衡状态,根据平衡条件可判
断,与物体相连的细绳拉力大小等于物体的重力.分别取 C 点和 P
点为研究对象,进行受力分析如图甲和乙所示.
甲
乙
图甲中,轻绳 AD 跨过定滑轮拉住质量为 M1 的物体,物体处
于平衡状态,绳 AC 段的拉力
FAC=FCD=M1g
图乙中,由 FEPsin 30°=FPQ=M2g
得 FEP=2M2g
对称法解决非共面力问题
在力的合成与分解的实际问题中,经常遇到物体受多个非共
面力作用处于平衡状态的情况,而在这类平衡问题中,又常有图
形结构对称的特点,结构的对称性往往对应着物体受力的对称性.
解决这类问题的方法是根据物体受力的对称性,结合力的合
成与分解知识及平衡条件列出方程,求解结果.
【典题 7】(2023 年广东梅州二模)梅州的非物质文化遗产有不
少,兴宁花灯就是其中一种,它与北京宫灯是一脉相承,始于宋代,
流行于明清,是传承了上千年的客家传统习俗,
花灯用四条长度相同,承受能力相同的绳子高
高吊起,如图所示,绳子与竖直方向夹角为 θ,
)
花灯质量为 m,则下列说法正确的是(
A.每条绳子的拉力均相同
B.增大绳子与竖直方向的夹角,花灯受的合外力增大
C.绳子拉力的合力方向为竖直方向
D.绳子长一些更易断
解析:每条绳子的拉力的大小相等,但力的方向不一样,A
错误;由于花灯处于静止状态,所以合外力始终为零,所以增大绳
子与竖直方向的夹角,花灯受的合外力不变,B 错误;合外力始终
为零,绳子拉力的合力与重力等大反向,故绳子拉力的合力方向
为竖直方向,C正确;设绳子拉力为 T,则 4Tcos θ=mg,解得 T=
mg
4cos θ
,绳子长一些,夹角θ减小,则拉力变小,不容易断,D 错
误.
答案:C
【触类旁通】(2024 年广东深圳二模)如图为我国传统豆腐制
作流程中用到的过滤器,正方形纱布的四角用细绳系在两根等长
的、相互垂直的水平木杆两端,再通过木杆中心转轴静止悬挂在
空中.豆浆过滤完,纱布与豆渣的总质量为 m,细绳与竖直方向的
夹角始终为θ.下列说法正确的是(
)
C.豆浆从纱布流出过程中,忽略纱布的拉伸形变,细绳受到
的拉力变大
D.豆浆从纱布流出过程中,纱布中豆浆和豆渣整体的重心
不变
答案:A
第2节
力的合成与分解
一、力的合成
1.合力与分力.
合
分
等效替代
合成
(1)定义:如果一个力单独作用的效果与几个力同时作用的共
同效果相同,这个力就叫那几个力的________力,而那几个力就
叫这个力的________力.
(2)关系:合力与分力之间在效果上是____________的关系.
(3)力的合成与分解:求几个力的合力的过程叫力的________,
求一个力的分力的过程叫力的分解.
2.平行四边形定则.
对角线
大小
(1)平行四边形定则:求两个互成角度的共点力 F1、F2 的合力,
可以用表示 F1、F2 的有向线段为边作平行四边形,平行四边形的
__________(在两个有向线段 F1、F2 之间)就表示合力的________
和方向,如图甲所示.
(2)三角形定则:求两个互成角度的共点力 F1、F2 的合力,可
以把表示 F1、F2 的线段________顺次相接地画出,把 F1、F2 的另
外两端连接起来,则此连线就表示______的大小和方向,如图乙
所示.
首尾
合力
特别提醒:(1)两个分力一定时,夹角θ越大,合力越小.
(2)合力一定时,两等大分力的夹角θ越大,两分力越大.
(3)合力可以大于分力,等于分力,也可以小于分力.
二、力的分解
分力
平行四边形
1.概念:求一个力的________的过程.
2.遵循的原则:______________定则或三角形定则.
3.分解的方法:
作用效果
正交
(1)按力产生的_______________进行分解,如图乙所示.
(2)将已知力按互相垂直的两个方向进行分解——________分
解,如图丙所示.
甲
丙
乙
【基础自测】
1.判断下列题目的正误.
(1)合力及其分力可以同时作用在物体上.(
)
(2)几个力的共同作用效果可以用一个力来代替.(
)
(3)两个力的合力一定比其分力大.(
)
(4)互成角度(非 0°或 180°)的两个力的合力与分力间一定构
成封闭的三角形.(
)
(5)两分力大小一定,夹角越小,合力越大.(
)
答案:(1)× (2)√ (3)× (4)√ (5)√
2.如图所示,F1、F2、F3 三个力恰好构成封闭的直角三角形,
则这三个力的合力大小为( )
A.0
B.2F1
C.2F2
D.2F3
解析:由矢量合成的法则可知,F1 与 F3 的合力为 F2,则这三
个力的合力大小为 2F2,选 C.
答案:C
)
3.关于力的合成与分解,下列说法正确的是(
A.合力一定大于任意一个分力
B.合力、分力大小是可以全部相等的
C.分力、合力一定不能都在一条直线上
D.合力大小不可能等于两个分力中的任何一个
答案:B
4.已知竖直平面内有一个大小为 10 N 的力作用于 O 点,该力
与x 轴正方向之间的夹角为30°,与 y 轴正方向之间的夹角为60°,
)
现将它分解到 x 轴和 y 轴方向上,则(
解析:画出坐标及受力情况,如图所示,已知两分力方向,
Fsin 30°=5 N.
答案:B
热点 1 力的合成
[热点归纳]
1.两个共点力的合力范围.
|F1-F2|≤F≤F1+F2.
2.重要结论.
(1)两个分力一定时,夹角θ越大,合力越小.
(2)合力一定时,两等大分力夹角θ越大,两分力越大.
(3)合力可以大于分力,等于分力,也可以小于分力.
3.力合成的方法.
(1)作图法.
(2)计算法.
若两个力 F1、F2 的夹角为θ,如图所示,
合力的大小可由余弦定理得到:
4.三个共点力的合成.
(1)最大值:三个力共线且同向时,其合力最大,为 F1+F2+
F3.
(2)最小值:任取两个力,求出其合力的范围,如果第三个力
在这个范围之内,则三个力的合力的最小值为零.如果第三个力不
在这个范围内,则合力的最小值为最大的一个力减去另外两个较
小的力的大小之和.
5.几种特殊情况的共点力的合成.
【典题 1】(2023 年广东广州二模)耙在中国已有 1500 年以
上的历史,北魏贾思勰所著的《齐民要术》中称之为“铁齿楱”,
将使用此农具的作业称作耙.如图甲所示,牛通过两根耙索拉耙
沿水平方向匀速耙地.两根耙索等长且对称,延长线的交点为O1,
夹角∠AO1B=60°,拉力大小均为 F,平面 AO1B 与水平面的
夹角为 30°(O2 为 AB 的中点),如图乙所示.忽略耙索质量,下
列说法正确的是(
)
乙
甲
A.两根耙索的合力大小为 F
答案:B
思路导引
三个力合力的最大值为三者之和,最小值分两种
情况讨论:若三力能构成三角形,合力最小值为 0;若不能构成三
角形,最小值为最大的力减去另外两个力所得的差.分析 C、D 选
项时,可参照上述思路.
【迁移拓展1】(2024 年广东广州模拟)如图所示俯视图,当汽
车陷入泥潭时,需要救援车辆将受困车辆拖拽驶离.救援人员发现
在受困车辆的前方有一坚固的树桩可以利用,根据你所学过的知
识判断,下列情况中,救援车辆用同样的力拖拽,受困车辆受到
的拉力最大的方案为(
)
A
B
C
D
解析:A 图中,根据受力分析可知,救援车辆的拉力为受困
车辆所受拖拽力的一半;B 图中,根据受力分析可知,救援车辆
的拉力为缆绳两侧拖拽拉力的合力,因初始时刻两分力夹角接近
180°,合力远小于两分力(小于所受拖拽力的一半);C图中,缆绳
与树桩构成定滑轮系统,仅改变力的方向,未改变力的大;D 图
中,根据受力分析可知,救援车辆的拉力为受困车辆所受拖拽力
的 2 倍;综上所述 B 图最省力,B 正确.
答案:B
热点 2 力的分解
考向 1 力的正交分解法
[热点归纳]
1.定义:将已知力按互相垂直的两个方向进行分解的方法.
2.步骤:如图所示,建立直角坐标系.通常选择共点力的作
用点为坐标原点,建立 x、y 轴让尽可能多的力落在坐标轴上.
3.把不在坐标轴上的各力向坐标轴进行正交分解.
【典题 2】(2021 年广东卷)唐代《耒耜经》记载了曲辕犁相对
直辕犁的优势之一是起土省力,设牛用大小相等的拉力 F 通过耕
索分别拉两种犁,F 与竖直方向的夹角分别为α 和β,α<β,如图
所示,忽略耕索质量,耕地过程中,下列说法正确的是( )
A.耕索对曲辕犁拉力的水平分力比对直辕犁的大
B.耕索对曲辕犁拉力的竖直分力比对直辕犁的大
C.曲辕犁匀速前进时,耕索对犁的拉力小于犁对耕索的拉力
D.直辕犁加速前进时,耕索对犁的拉力大于犁对耕索的拉力
解析:将拉力 F 正交分解如图所示.
则在 x 方向可得出 Fx曲=Fsin α,Fx直=Fsin β,在 y 方向可得
出 Fy曲=Fcos α,Fy直=Fcos β
由题知α<β则 sin α
一对相互作用力,它们大小相等,方向相反,无论是加速还是匀速,
则 CD 错误.
答案:B
实例 分解思路
拉力F可分解为水平分力F1=Fcos α和竖直分力F2=Fsin α
重力分解为使物体沿斜面向下的分力F1=mg sin α和使物体压紧斜面的分力F2=mg cos α
考向 2 力的按效果分解
[热点归纳]
1.常见的按力产生的效果进行分解的情形.
实例 分解思路
重力分解为使球压紧挡板的分力 F1=mg tan α和使球
mg
压紧斜面的分力 F2=
cos α
重力分解为使球压紧竖直墙壁的分力 F1=mg tan α和
mg
使球拉紧悬线的分力 F2=
cos α
(续表)
实例 分解思路
重力分解为使球拉紧 AO 线的分力 F2 和使球拉紧 BO
mg
线的分力 F1,大小 F1=F2=
2sin α
(续表)
2.按实际效果分解力的一般思路.
3.力的分解方法选取原则.
(1)一般来说,当物体受到三个或三个以下的力时,常按实际
效果进行分解,若这三个力中,有两个力互相垂直,优先选用正
交分解法.
(2)当物体受到三个以上的力时,常用正交分解法.
【典题3】(2024 年广东佛山开学考)如图甲所示是斧子砍进木
桩时的情境,其横截面如图乙所示,斧子的剖面可视作顶角为θ的
等腰三角形,当施加竖直向下的力 F 时,则(
)
甲
乙
B.施加的力 F 越小,斧头对木桩的侧向压力越大
C.施加相同的力 F,θ越大的斧子,越容易劈开木桩
D.施加相同的力 F,θ越小的斧子,越容易劈开木桩
解析:将力 F 进行分解,如图所示.
答案:D
思路导引
本题除了应用分解的方法分析外,同样可以应用
合成的方法:两个分力 F1、F2 的合力大小等于 F,结合图中四边
形为菱形的特点,应用几何关系求解.
已知条件 示意图 解的情况
已知合力与两个分力的方向,并且不在一条直线上
有唯一解
考向 3 力的分解中的多解问题
[热点归纳]
已知条件 示意图 解的情况
已知合力与两个分
力的大小 在同一平面内有两解或无解(当F<|F1-F2|或F>F1+F2时无解)
(续表)
已知条件 示意图 解的情况
已知合力与一个分
力的大小和方向
有唯一解
(续表)
已知条件 示意图 解的情况
已知合力与一个分力的大小及另一个分力的方向 在0<θ<90°时有三种情况:
①当F1=F sin θ或F1>F时,有一组解;
②当F1
(续表)
【典题 4】已知两个共点力 F1、F2 的合力 F 大小为 10 N,力
F1 的大小为 6 N,力 F2 的方向与合力 F 的方向的夹角为θ,则θ的
值可能为(arcsin 0.6=37°)( )
A.30°
B.45°
C.60°
D.90°
2023年广东深圳开学考
解析:以合力 F 的起点为圆心,以表示 6 N 大小为半径作图,
答案:A
如图所示.则连接F的终点和圆上的任意一点均可以得出 F2的大小和方向,当F2与圆相切时得到的夹角最大,由几何定律可知,
是可能的,选项中只有 A 符合,A 正确.
“死结”模型 “活结”模型
“死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点.“死结”两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等 “活结”可理解为把绳子分成两段,且可以沿绳子移动的结点.“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的.绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的平分线
热点 3 绳模型、杆模型
1.轻绳模型.
【典题 5】如图,悬挂甲物体的细线拴牢在一不可伸长的轻
质细绳上 O 点处,绳的一端固定在墙上,另一端通过光滑定滑轮
与物体乙相连.甲、乙两物体质量相等.系统平衡时,O 点两侧绳与
竖直方向的夹角分别为α和β.若α=70°,则β等于( )
A.45°
B.55°
C.60°
D.70°
解析:甲物体是拴牢在 O 点,且甲、乙两物体的质量相等,
则甲、乙绳的拉力大小相等,O 点处于平衡状态,则左侧绳子拉
力的方向在甲、乙绳子的角平分线上,如图所示.根据几何关系
有 180°=2β+α,解得β=55°,故选 B.
答案:B
【迁移拓展 2】如图所示,M、 N 两支架固定在高台边缘,
钢绳两端连接到两个支架上等高的位置,钢绳的长度可通过固定
在支架 M 上的电动机收放.某杂技演员(可视为质点)抓住套在钢绳
上的滑环静止在高空,滑环可沿钢绳无摩擦滑动.则下列说法正确
的是( )
)
A.若启动电动机使钢绳缓慢缩短,钢绳拉力将不断减小
B.若启动电动机使钢绳缓慢缩短,左侧钢绳拉力将增大,右
侧钢绳拉力将减小
C.若启动电动机使钢绳缓慢伸长,钢绳拉力将不断减小
D.若启动电动机使钢绳缓慢伸长,演员运动的轨迹为偏向支
架 N 一侧的曲线
解析:设滑环两侧钢绳与水平面的夹角为θ,对杂技演员由平
衡条件可得 2Tsin θ=mg,若启动电动机使钢绳缓慢缩短,则θ减
小,两侧钢绳拉力将不断增大,若启动电动机使钢绳缓慢伸长,
则θ增大,两侧钢绳拉力将不断减小,C 正确,AB 错误;由于钢
绳两端连接到两个支架上等高的位置,同一条钢绳上拉力大小处
处相等,由对称性可知,滑环两侧钢绳与水平面的夹角总是相等,
故启动电动机使钢绳缓慢伸长,演员运动的轨迹为竖直向下,若
演员运动的轨迹偏向支架 N 一侧,滑环两侧的钢绳与水平面的夹
角就不会相等,D 错误.
答案:C
“动杆”模型 “定杆”模型
对于一端有转轴或有铰链的轻杆,其提供的弹力方向一定是沿着轻杆的方向 一端固定的轻杆(如一端“插入”墙壁或固定于地面),其提供的弹力不一定沿着轻杆的方向,力的方向只能根据具体情况进行受力分析.根据平衡条件或牛顿第二定律确定杆中的弹力的大小和方向
2.轻杆模型.
【典题 6】如图甲所示,轻绳 AD 跨过固定在水平横梁BC 右
端的定滑轮挂住一个质量为10 kg的物体,∠ACB=30°;图乙中轻
杆 HP 一端用铰链固定在竖直墙上,另一端P通过细绳EP拉住,EP
与水平方向也成 30°,轻杆的 P 点用细绳 PQ 拉住一个质量也为
10 kg 的物体.g 取 10 N/kg,求轻绳 AC 段的拉力大小 FAC 与细绳 EP
段的拉力大小 FEP 之比.
甲
乙
解:题图中的两个物体都处于平衡状态,根据平衡条件可判
断,与物体相连的细绳拉力大小等于物体的重力.分别取 C 点和 P
点为研究对象,进行受力分析如图甲和乙所示.
甲
乙
图甲中,轻绳 AD 跨过定滑轮拉住质量为 M1 的物体,物体处
于平衡状态,绳 AC 段的拉力
FAC=FCD=M1g
图乙中,由 FEPsin 30°=FPQ=M2g
得 FEP=2M2g
对称法解决非共面力问题
在力的合成与分解的实际问题中,经常遇到物体受多个非共
面力作用处于平衡状态的情况,而在这类平衡问题中,又常有图
形结构对称的特点,结构的对称性往往对应着物体受力的对称性.
解决这类问题的方法是根据物体受力的对称性,结合力的合
成与分解知识及平衡条件列出方程,求解结果.
【典题 7】(2023 年广东梅州二模)梅州的非物质文化遗产有不
少,兴宁花灯就是其中一种,它与北京宫灯是一脉相承,始于宋代,
流行于明清,是传承了上千年的客家传统习俗,
花灯用四条长度相同,承受能力相同的绳子高
高吊起,如图所示,绳子与竖直方向夹角为 θ,
)
花灯质量为 m,则下列说法正确的是(
A.每条绳子的拉力均相同
B.增大绳子与竖直方向的夹角,花灯受的合外力增大
C.绳子拉力的合力方向为竖直方向
D.绳子长一些更易断
解析:每条绳子的拉力的大小相等,但力的方向不一样,A
错误;由于花灯处于静止状态,所以合外力始终为零,所以增大绳
子与竖直方向的夹角,花灯受的合外力不变,B 错误;合外力始终
为零,绳子拉力的合力与重力等大反向,故绳子拉力的合力方向
为竖直方向,C正确;设绳子拉力为 T,则 4Tcos θ=mg,解得 T=
mg
4cos θ
,绳子长一些,夹角θ减小,则拉力变小,不容易断,D 错
误.
答案:C
【触类旁通】(2024 年广东深圳二模)如图为我国传统豆腐制
作流程中用到的过滤器,正方形纱布的四角用细绳系在两根等长
的、相互垂直的水平木杆两端,再通过木杆中心转轴静止悬挂在
空中.豆浆过滤完,纱布与豆渣的总质量为 m,细绳与竖直方向的
夹角始终为θ.下列说法正确的是(
)
C.豆浆从纱布流出过程中,忽略纱布的拉伸形变,细绳受到
的拉力变大
D.豆浆从纱布流出过程中,纱布中豆浆和豆渣整体的重心
不变
答案:A
同课章节目录
