14.7一次函数的应用巩固强化练习(含解析)
文档属性
| 名称 | 14.7一次函数的应用巩固强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 17:26:48 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
14.7一次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
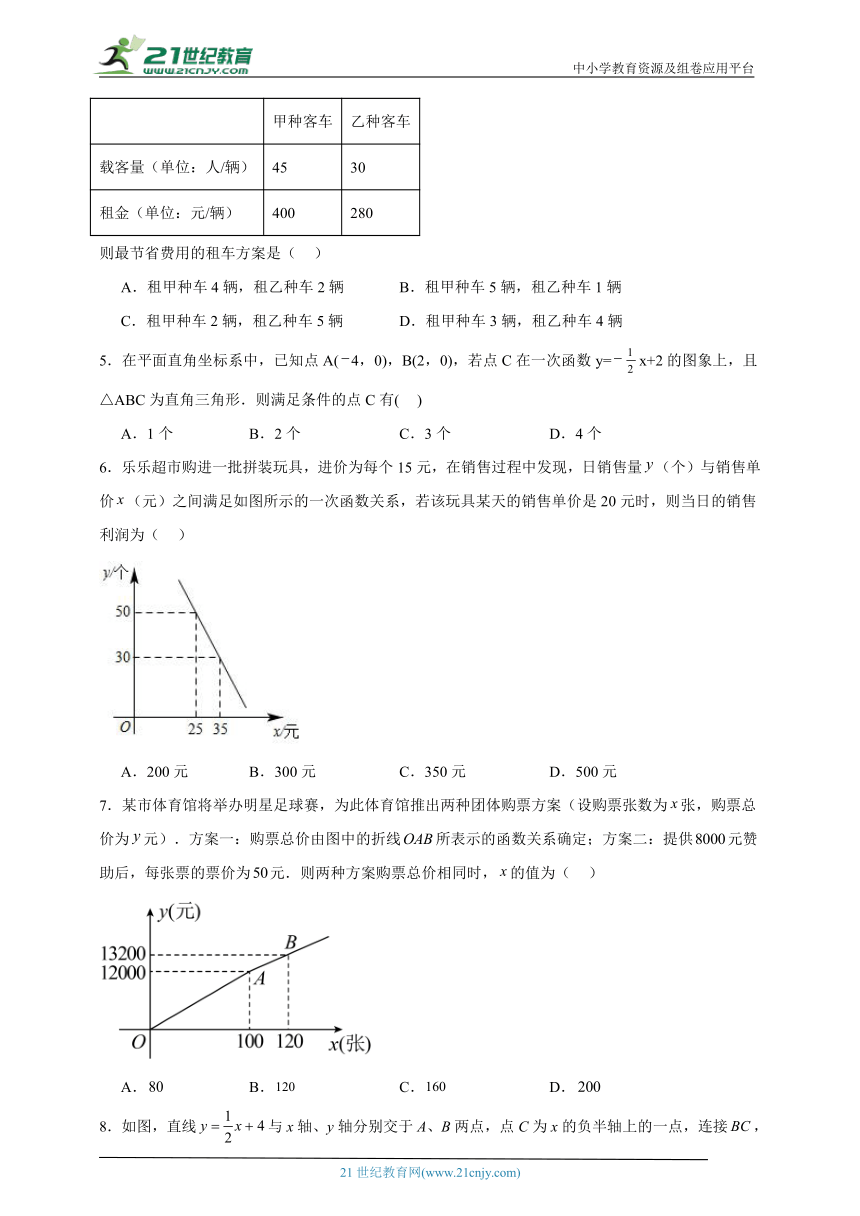
1.宾馆有100间相同的客房,经过一段时间的经营,发现客房定价与客房的入住率之间有下表所示的关系,按照这个关系,要使客房的收入最高,每间客房的定价应为( )
每间房价(元)
入住率
A.300元 B.280元 C.260元 D.220元
2.某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲,乙两仓库的快件数量(件)与时间(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A.9:15 B.9:20 C.9:25 D.9:30
3.商户小李以每件元的价格购进某商品若干件到市场去销售,销售金额元与销售量件的函数关系的图象如图所示,则降价后每件商品销售获得的利润为( )
A.元 B.元 C.元 D.元
4.某学校计划租用甲、乙两种客车送240名师生(其中学生233名、教师7名)集体外出活动,要求每辆客车上至少要有1名教师.甲、乙两种客车的载客量和租金如下表:
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金(单位:元/辆) 400 280
则最节省费用的租车方案是( )
A.租甲种车4辆,租乙种车2辆 B.租甲种车5辆,租乙种车1辆
C.租甲种车2辆,租乙种车5辆 D.租甲种车3辆,租乙种车4辆
5.在平面直角坐标系中,已知点A(4,0),B(2,0),若点C在一次函数y=x+2的图象上,且△ABC为直角三角形.则满足条件的点C有( )
A.1个 B.2个 C.3个 D.4个
6.乐乐超市购进一批拼装玩具,进价为每个15元,在销售过程中发现,日销售量(个)与销售单价(元)之间满足如图所示的一次函数关系,若该玩具某天的销售单价是20元时,则当日的销售利润为( )
A.200元 B.300元 C.350元 D.500元
7.某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为张,购票总价为元).方案一:购票总价由图中的折线所表示的函数关系确定;方案二:提供元赞助后,每张票的票价为元.则两种方案购票总价相同时,的值为( )
A. B. C. D.
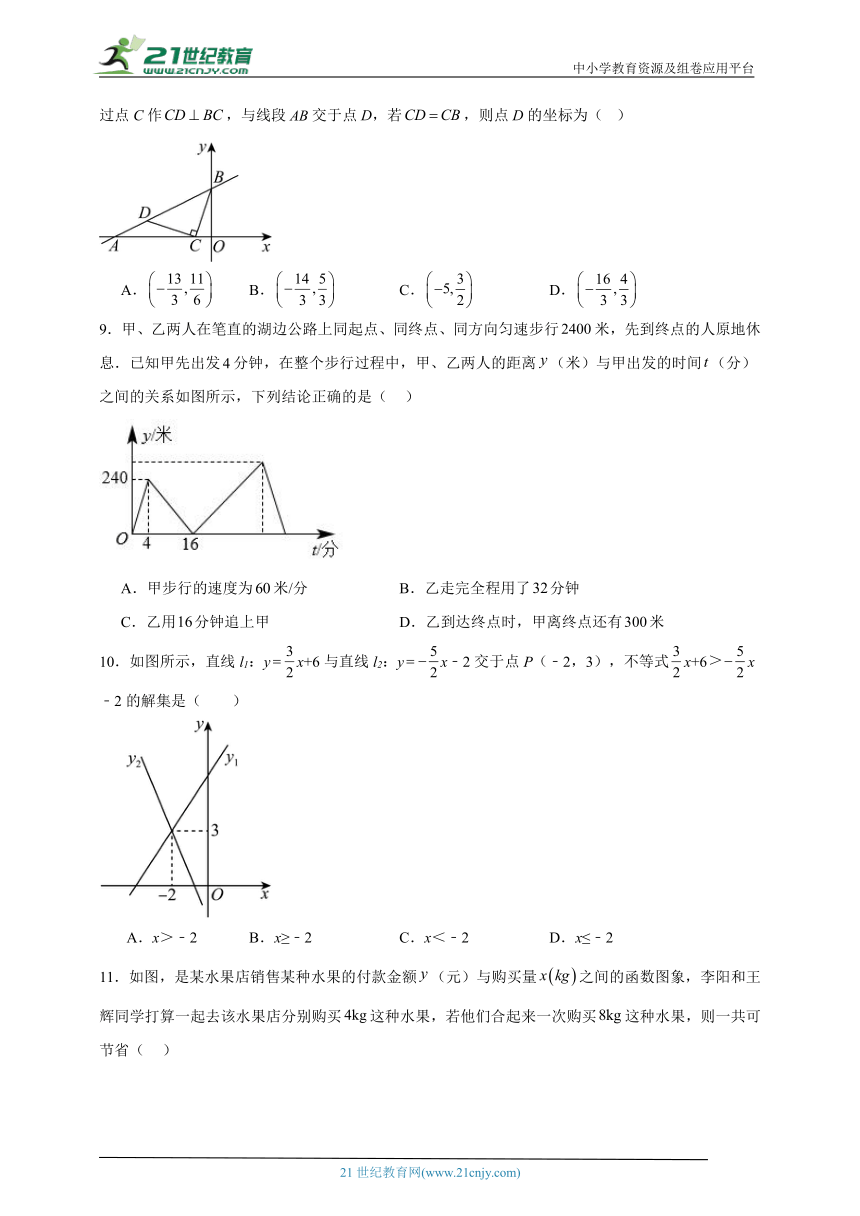
8.如图,直线与x轴、y轴分别交于A、B两点,点C为x的负半轴上的一点,连接,过点C作,与线段交于点D,若,则点D的坐标为( )
A. B. C. D.
9.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行米,先到终点的人原地休息.已知甲先出发分钟,在整个步行过程中,甲、乙两人的距离(米)与甲出发的时间(分)之间的关系如图所示,下列结论正确的是( )
A.甲步行的速度为米/分 B.乙走完全程用了分钟
C.乙用分钟追上甲 D.乙到达终点时,甲离终点还有米
10.如图所示,直线l1:yx+6与直线l2:yx﹣2交于点P(﹣2,3),不等式x+6x﹣2的解集是( )
A.x>﹣2 B.x≥﹣2 C.x<﹣2 D.x≤﹣2
11.如图,是某水果店销售某种水果的付款金额(元)与购买量之间的函数图象,李阳和王辉同学打算一起去该水果店分别购买这种水果,若他们合起来一次购买这种水果,则一共可节省( )
A.6元 B.5元 C.4元 D.3元
12.如图所示,已知点,一次函数的图象与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则的最小值是( )
A.4 B.5 C. D.
二、填空题
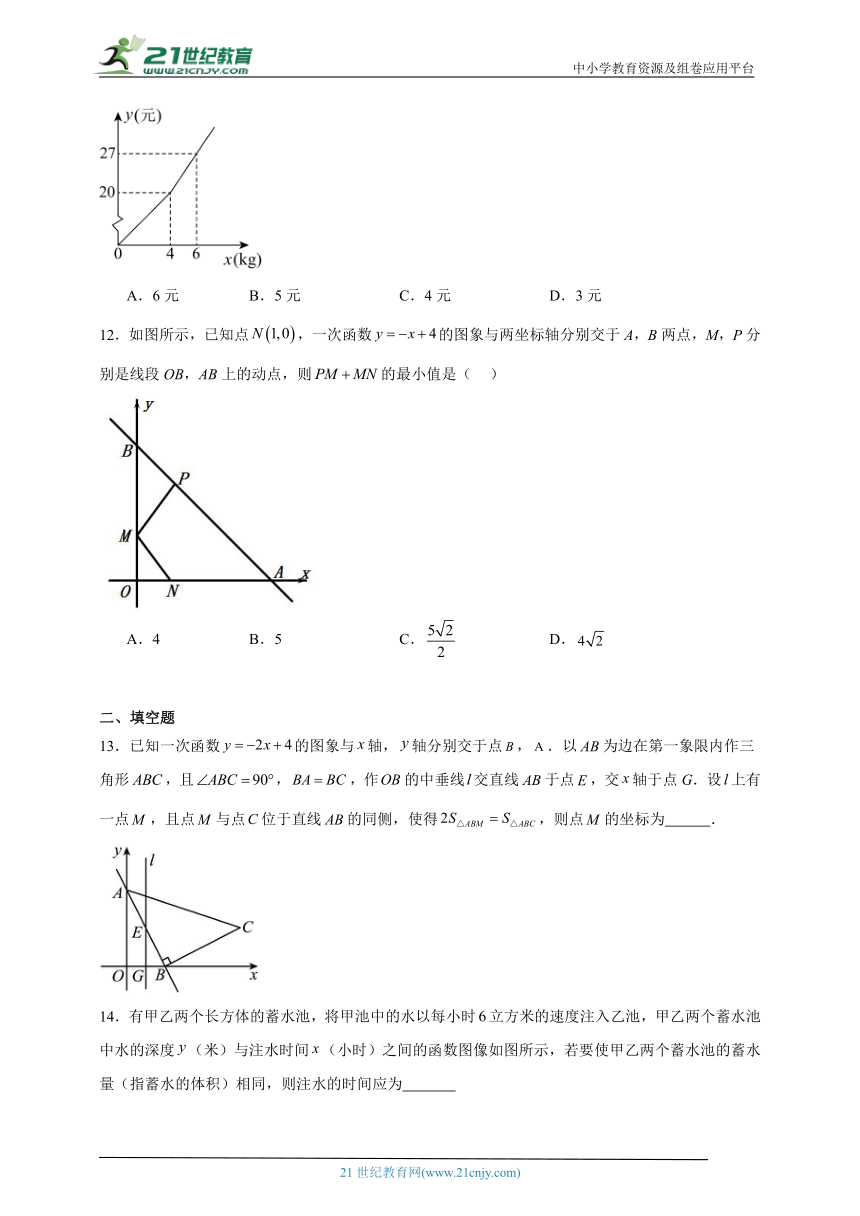
13.已知一次函数的图象与轴,轴分别交于点,.以为边在第一象限内作三角形,且,,作的中垂线交直线于点,交轴于点G.设上有一点,且点与点位于直线的同侧,使得,则点的坐标为 .
14.有甲乙两个长方体的蓄水池,将甲池中的水以每小时立方米的速度注入乙池,甲乙两个蓄水池中水的深度(米)与注水时间(小时)之间的函数图像如图所示,若要使甲乙两个蓄水池的蓄水量(指蓄水的体积)相同,则注水的时间应为
15.观察下表,知方程的解是 .
16.如图,购买一种商品,付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次性购买50千克这种商品要付款 元.
17.一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始内只进水不出水,从第到第内既进水又出水,从第开始只出水不进水,容器内水量(单位:)与时间(单位:)之间的关系如图所示,则图中的值是 .
三、解答题
18.某便利店老板购进了A,B两种口罩各100包供甲、乙两个便利店进行销售,预计两个店每包口罩的利润(单位:元)如下表:
A种口罩 B种口罩
甲店 a b
乙店 0.8 1
(1)若甲店销售A种口罩30包,B种口罩40包,可以盈利86元;销售A种口罩20包,B种口罩60包,可以盈利104元,求甲店这两种口罩每包的利润各是多少元.
(2)若甲、乙两个便利店各配货100包口罩,且保证乙店总利润不小于92元的条件下,请你设计出使便利店老板盈利最大的配货方案,并求出最大利润.
19.某空调厂的装配车间原计划用2个月时间(每月以30天计算),每天组装150台空调.
(1)从组装空调开始,组装的台数(单位:台/天)与生产的时间(单位:天)之间有怎样的函数关系?
(2)由于气温提前升高、厂家决定这批空调提前十天上市,那么装配车间每天至少要组装多少空调?
20.如图,∠MBN的两边BM,BN上分别有两点A、C,满足BC=2BA,作□ABCD,取AD的中点E,作CF⊥CD,CF与AB所在的直线交于点F.
(1)当∠B=时,直接写出∠DEF的度数;
(2)在射线BM绕B点旋转的过程中,若∠B=,∠DEF=(<X<,<Y<),求:Y关于X的函数解析式及相应自变量X的取值范围,
21.为了丰富同学们的课余生活,经市场了解,发现篮球的单价比足球的单价多元,用元购买的篮球的个数等于用元购买的足球的个数.
(1)求篮球和足球的单价
(2)为了支持学校开展体育活动,某校准备购买足球、篮球共个,且保证购买篮球数量不少于足球的一半,商店对篮球及足球进行打折销售,其中篮球打八折,足球打九折,请你给该校设计一个最省钱的购买方案,并求出最少费用为多少元?
22.如图所示,平面直角坐标系中,直线l1:y=﹣2x+3与直线l2:y=x+1相交于点A,直线l2与x轴相交于点B.过直线l2上的一点P(a,﹣1)作y轴的垂线,交直线l1于点C,连接BC.
(1)求点A的坐标;
(2)求△ABC的面积;
(3)将直线l1向下平移4个单位长度得到直线l3,设直线l3与y轴相交于点D,则直线l2上是否存在一点Q,使得△DPQ是以DP为腰的等腰三角形?若存在,请直接写出Q的坐标,若不存在,请说明理由.
23.为了迎接兔年的到来,广大市民纷纷开始购买兔年装饰物,某网店上架了“玉兔灯笼”和“玉兔摆件”这两款产品,已知10个“玉兔灯笼”和15个“玉兔摆件”的售价为2400元;30个“玉兔灯笼”和20个“玉兔摆件”的售价为5200元.
(1)每个“玉兔灯笼”和“玉兔摆件”的售价分别为多少元?
(2)已知“玉兔灯笼”和“玉兔摆件”的成本分别为80元/个和50元/个.进入2023年一月后,这两款产品持续热销,于是网店再购进了这两款产品共600个,其中“玉兔摆件”的数量不超过“玉兔灯笼”数量的2倍,且购进总价不超过37800元.为回馈新老客户,网店决定对“玉兔灯笼”降价10%后再销售,若一月份购进的这两款产品全部售出,则“玉兔灯笼”购进多少个时该网店当月销售利润最大?最大利润为多少?
24.“十一”黄金周期间,欢欢一家随旅游团到某风景区旅游,集体门票的收费标准是:人以内(含 人),每人元;超过人的,超过的部分每人元.
()写出应收门票费(元)与游览人数(人)(其中)之间的关系式.
()利用()中的关系式计算:若欢欢一家所在的旅游团共人,那么该旅游团购门票共花了多少钱?
《14.7一次函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C A D B D D A A
题号 11 12
答案 A C
1.C
【详解】当每间客房的定价为300元时,客房的收入为100×65%×300=19500(元);
当每间客房的定价为280元时,客房的收入为100×75%×280=21000(元);
当每间客房的定价为260元时,客房的收入为100×85%×260=22100(元);
当每间客房的定价为220元时,客房的收入为100×95%×220=20900(元).
所以当每间客房的定价为260元时,客房的收入最高.故选C.
2.B
【分析】分别求出甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数关系式,求出两条直线的交点坐标即可.
【详解】设甲仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y1=k1x+40,根据题意得60k1+40=400,解得k1=6,
∴y1=6x+40;
设乙仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y2=k2x+240,根据题意得60k2+240=0,解得k2=-4,
∴y2=-4x+240,
联立,解得,
∴此刻的时间为9:20.
故选B.
【点睛】本题考查了一次函数的应用,解题的关键:(1)熟练运用待定系数法就解析式;(2)解决该类问题应结合图形,理解图形中点的坐标代表的意义.
3.C
【分析】本题考查一次函数的利润问题.先根据图象得到降价后的售价,然后利用公式计算利润率即可.
【详解】解:∵由图象可知件销售金额为元,件的销售金额为元,
∴降价后卖了件,销售金额为元,
∴降价后每件商品销售的价格为元,
∴降价后每件商品的销售利润为元,
故选:C.
4.A
【分析】设租用甲客车x辆,租车总费用y元,由每辆客车上至少要有1名教师可知客车总数不能大于7辆,要保证240名师生有车坐,客车总数不能小于,客车总数不能小于6,可得客车总数为6,,根据题意列出一次函数和一元一次不等式,找到x的取值范围,再结合一次函数的增减性即可求解.
【详解】解:设租用甲客车x辆,租车总费用y元,由每辆客车上至少要有1名教师可知客车总数不能大于7辆,
要保证240名师生有车坐,客车总数不能小于,客车总数不能小于6,
∴客车总数为6,,
由题意可得,,
整理可得,
由题意,,
解得,
∵,
∴,
∵中,,y随x的增大而增大,
∴x取最小值时,即,y有最小值,
即当租甲种车4辆,租乙种车2辆,费用最少,
故选:A.
【点睛】本题考查一次函数和一元一次不等式的实际应用,利用题中的不等关系找到x的取值范围是解题的关键.
5.D
【详解】由题意知,直线y= x+2,与x轴的交点为(4,0),与y轴的交点为
(0,2),如图:
过点A作垂线与直线的交点W(-4,4),
过点B作垂线与直线的交点S(2,1),
过AB中点E(-1,0),作垂线与直线的交点为F(-1,2.5),
则EF=2.5<3,
所以以3为半径,以点E为圆心的圆与直线必有两个交点
∴共有四个点能与点A,点B组成直角三角形.
故选D.
6.B
【分析】根据题意,利用待定系数法求出与的一次函数关系式,然后将代入即可求出销售量,最后利用销售收入减去成本支出即可求出销售利润.
【详解】解:设与的一次函数关系式为,
由图可得,
解得,
所以与的一次函数关系式为,
把代入可得,
所以销售利润为(元).
故选B.
【点睛】本题考查求一次函数的关系式和利润问题,熟练掌握待定系数法求一次函数的关系式是解题的关键.
7.D
【分析】分别求出方案一中的OA和AB表示的解析式以及方案二的解析式,再进行比较即可得到结论.
【详解】解:在方案一中,设OA表示的解析式为,且
解得,
表示的解析式为:;
设表示的解析式为,
又,
解得,,
表示的解析式为:;
方案二的解析式为:;
当时,
故的图象与的图象无交点,
当时,,
所以,当时,两种方案购票总价相同.
故选:D.
【点睛】此题主要考查了一次函数的应用,运用待定系数法求一次函数关系式是解答本题的关键.
8.D
【分析】本题主要考查一次函数与几何综合,由直线求出点坐标,得出,过点D作于点E,证明,得,设点,则,得出,代入,求出的值即可.
【详解】解:对于,当时,,
∴,
∴,
过点D作于点E,如图,
则
∴,
∵,
∴
∴
∴,
又
∴,
∴,
设点,则,
∴,
把代入,得,
解得,,
∴,
故选:D.
9.A
【分析】根据题意和函数图象中的数据可以判断各个小题中的结论是否正确,从而可以解答本题.
【详解】由图可得,
甲步行的速度为:米/分,故正确,
乙走完全程用的时间为:(分钟),故错误,
乙追上甲用的时间为:(分钟),故错误,
乙到达终点时,甲离终点距离是:米,故错误,
故选.
【点睛】本题主要考查一次函数的实际应用、函数的图象,能从函数的图象中获取相关信息解决问题是解答的关键.
10.A
【分析】利用函数图象写出直线l1:y=x+6与在直线l2:y=-x-2上方所对应的自变量的范围即可.
【详解】当x>﹣2时,x+6x﹣2,
所以不等式x+6x﹣2的解集是x>﹣2.
故选A.
【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
11.A
【分析】本题考查了一次函数的应用.根据题意求出时与之间的函数关系式,再把代入计算可得答案.
【详解】解:当时,设与之间的函数关系式为,根据题意得:
,
解得,
,
当时,(元),
由图象可知,单独购买这种水果需要20元,
(元),
即若他们合起来一次购买这种水果,则一共可节省6元.
故选:A.
12.C
【分析】如图,点N关于OB的对称点N′(-1,0),过点N′作N′P⊥AB交OB于M,则PN′=PM+MN的最小值,根据直线AB的解析式为y=-x+4,得到直线N′P的解析式为y=x+1,得到,推出△PAN′是等腰直角三角形,于是得到结论.
【详解】解:如图,点N关于OB的对称点N′(-1,0),过点N′作N′P⊥AB交OB于M,
则PN′=PM+MN的最小值,
∵直线AB的解析式为y=-x+4,
∴A(4,0),B(0,4),
∴直线N′P的解析式为y=x+1,
由 解得
,
∵A(4,0),B(0,4),
∴OA=OB,
∴∠BAO=45°,
∴△PAN′是等腰直角三角形,
∵AN′=4+1=5,
∴
∴PM+MN的最小值是
故选:C
【点睛】本题考查一次函数的应用,等腰三角形的判定和性质等知识,解题的关键是利用对称性找到点M、点P位置,属于中考常考题型.
13.
【分析】先求出、两点的坐标,根据是的中垂线,则点,当时,,即点,故可得出的长;设,求出的面积,由,得到,即可求解;
【详解】解:如图,
是的中垂线,
点,
当时,即,
设
解得:
故答案为:.
【点睛】本题考查的是一次函数图象上点的坐标特点,涉及到三角形全等、中垂线的性质、勾股定理的运用,正确作出辅助线是解题的关键.
14.小时
【分析】本题考查用一次函数解决实际问题,先根据图像分别求出甲、乙两个蓄水池中水的深度与注水时间之间的函数关系式;设甲蓄水池的底面积为,乙蓄水池的底面积为,小时甲乙两个蓄水池的蓄水量相同,列出方程解答即可.正确理解题意并建立方程是解题的关键.
【详解】解:设,过点,,
得:,
解得:,
∴,
设,过点,,
得:,
解得:,
∴,
设甲蓄水池的底面积为,乙蓄水池的底面积为,小时甲乙两个蓄水池的蓄水量相同,
∵甲乙两个长方体的蓄水池,将甲池中的水以每小时立方米的速度注入乙池,甲水深度下降米,而乙水池深度升高米,
∴,,
∴,,
∴,即,
解得:,
∴注水小时甲、乙两个蓄水池的蓄水量相同.
故答案为:小时.
15.
【分析】设,要求方程的解,就是求函数当y=2450时对应的x的值,观察表格即可得出.
【详解】解:设,由题中所给表格,可知当时,,所以方程的解是.
【点睛】本题考查了一次函数与一元一次方程的关系,本题重在理解,即要求方程的解,就是求函数当y=2450时对应的x的值,前者是从数的角度,后者是从形的角度,数形结合,相得益彰.
16.420
【分析】当x>10时,用待定系数法求函数解析式即可.
【详解】解:当x>10时,付款金额y(元)与购买量x(千克)之间的函数为y=kx+b(k≠0),
∵图象过点(10,100)和(20,180),
∴,
解得:,
∴y与x的函数解析式为y=8x+20,
∴当x=50时,y=8×50+20=420,
一次性购买50千克这种商品要付款420元.
故答案为:420.
【点睛】本题考查一次函数的应用,解答本题的关键是求出射线AB段的函数解析式.
17.
【分析】根据图像可求出每分钟的进水量和出水量,运用待定系数求出直线的解析式,可求出时间为时容器中的水量,再根据从第开始只出水不进水,由此即可求解.
【详解】解:如图所示,
,,
∴每分钟的进水量为,即每分钟进水,
,,设每分钟出水量为,
∴,解得,,即每分钟出水量为,
设所在直线的解析式为,,,
∴,解得,,
∴直线的解析式为,
∵点在直线的图像上,且点的横坐标为,
∴,即,
∴当时,容器内水量,且每分钟出水量为,
根据题意得,,解得,,
故答案为:.
【点睛】本题主要考查一次函数图像与实际问题的综合运用,理解图像,掌握待定系数法求一次函数解析式是解题的关键.
18.(1)甲店A种口罩每包的利润是1元,B种口罩每包的利润是1.4元
(2)使便利店老板盈利最大的配货方案是:给甲店配送A种口罩60包.B种口罩40包.给乙店配送A种口罩40包,B种口罩60包,最大利润是208元
【分析】(1)根据题意,列出方程组求解即可.
(2)设给甲店配送A种口罩x包,B种口罩包,给乙店配送A种口罩包、B种口罩x包,两店总利润为W元.建立不等式求解即可.
【详解】(1)由题意,可列方程组,
解得
答:甲店A种口罩每包的利润是1元,B种口罩每包的利润是1.4元.
(2)设给甲店配送A种口罩x包,B种口罩包,给乙店配送A种口罩包、B种口罩x包,两店总利润为W元.
∵乙店总利润不小于92元,
∴,解得.
由题意,得.
∵.
∴W随x的增大而减小.
∴当时,W有最大值..
∴使便利店老板盈利最大的配货方案是:给甲店配送A种口罩60包.B种口罩40包.给乙店配送A种口罩40包,B种口罩60包,最大利润是208元.
【点睛】本题考查了方程组得应用,一次函数的应用,不等式的应用,熟练掌握方程组得解法,一次函数的应用是解题的关键.
19.(1),
(2)
【分析】本题考查了一元一次方程的应用,抓住全部装配的台数不变,建立等量关系.
(1)组装的台数等于每天组装的台数与天数的乘积;
(2)全部装配的台数不变,即台,而时间提前了10天,用时间装配速度全部装配的台数,建立方程.
【详解】(1)解:,;
(2)解:设装配车间每天至少要组装台空调,
依题意列方程:,
解得:.
答:装配车间每天至少要组装180台空调.
20.(1)∠DEF=135°°(2)当0°<∠B<60°时,y=90+x;当60°<∠B<180°时,y=270-x.
【详解】试题分析:(1) 当∠B=90°时, ABCD是矩形,则点F与点B重合,根据BC=2BA,点E是AD的中点,可得:AB=AE,所以∠ABE=∠AEB=45°,继而可得:∠DEF=180°-∠AEB=135°,
(2)对∠B的大小分三种情况讨论: ①当时,点F在线段AB上,,
②当时, 与①同理可得, ③当,F在线段BA的延长线上, y=.
试题解析:(1) 在 ABCD中,AD=BC,
当∠B=90°时, ABCD是矩形,则点F与点B重合,
∵BC=2BA,点E是AD的中点,
∴AB=AE,
∴∠ABE=∠AEB=45°,
∴∠DEF=180°-∠AEB=135°,即∠DEF=135°,
(2)对∠B的大小分三种情况讨论如下:
当时,点F在线段AB上(见图7-1),
延长FE,并与CD的延长线交于点G,记∠AFE=.
∵ ABCD,
∴ AB∥CD,AD=BC,AB=CD,∠3=∠B=x°,
∴ ∠DGE=∠AFE=,
可得 △AEF≌△DEG,
∴ EF=EG,CE为Rt△CFG斜边的中线,
∴ EF=EG,∠1=∠G=,
∵ BC=2AB,
∴ 2DE=2CD,DE=CD,
∴ 等腰三角形△CDE中,∠1==,
∴∠DEF=,
1>当∠B=90°时,F与点B重合,见图7-2) 此时∠DEF=135°,
所以仍成立,
2>当∠B=60°时,F与点A重合, ∠DEF=180°不合题意(见图7-3),
当时,F在线段AB的延长线上(见图7-4),
与①同理可得,
当,F在线段BA的延长线上(如图7-5),
与①同理可得CE为Rt△CFG斜边的中线,EC=EG,DE=CD,
∴ △CEG和△CDE为等腰三角形,
在等腰三角形△CEG中,∠1=180°-2∠2,在等腰三角形△CDE中,
,
∴ ∠DEF=180°-∠3=180°-(∠CED-∠1)=360°-3∠2=,
综上所述,当时,y=,
当时,.
21.(1)篮球的单价是,足球的单价是;
(2)最省钱的购买方案是:足球买个,篮球个,费用为.
【分析】(1)设足球的单价为x元,根据元购买的篮球的个数等于用元购买的足球的个数列方程即可得到答案;
(2)根据篮球数量不少于足球的一半列不等式,根据题意列出费用函数,根据函数性质即可得到最少方案.
【详解】(1)解:设足球的单价为x元,则篮球单价为元,由题意可得,
,
解得:,
∴,
∴篮球的单价是,足球的单价是;
(2)解:设购买足球m个,则篮球个,由题意可得,
且m为非负整数,
解得:的非负整数,
设费用为w,则有:
,
∵,
∴w随m增大而减小,
∴当时w最小,
最少费用为:,
∴最省钱的购买方案是:足球买个,篮球个,费用为.
【点睛】本题考查了分式方程的应用,一元一次不等式的应用,一次函数的性质,理解题意并根据题意求出函数关系式是解题的关键.
22.(1)
(2)
(3)存在,点Q坐标为:(﹣2,﹣1)或(﹣﹣2,﹣﹣1)或(0,1)
【分析】(1)联立方程组即可求解;
(2)分别求出点B,点P,点C坐标,再根据结合三角形的面积公式即可求解;
(3)先求出点D坐标,由等腰三角形的性质和两点之间的距离公式可求解.
【详解】(1)联立,
解得:,
∴点A(,);
(2)对于直线l2:,令,得:
解得:,
∴点B(-1,0).
∵点P(a,-1)在直线l2上,
∴-1=a+1,
解得:a=-2,
∴点P(-2,-1),
∴点C的纵坐标为-1.
对于直线l1:,当时,,
解得:x=2,
∴点C(2,-1),
∴
.
(3)存在,理由如下:
∵将直线l1向下平移4个单位长度得到直线l3,
∴直线l3的解析式为:,
∴点D(0,-1),
如图,
∵点P(-2,-1),点D(0,-1),
∴PD⊥y轴,PD=2,
设点Q(a,a+1),
∵△DPQ是以DP为腰的等腰三角形,
∴PQ=PD=2或PD=QD=2,
当PQ=PD=2时,则,
∴ ,
∴Q(,)或(,);
当PD=QD=2时,则,
∴a=0或-2(不合题意舍去),
∴Q(0,1),
综上所述:点Q坐标为:(,)或(,)或(0,1).
【点睛】本题为一次函数综合题.考查两直线的交点问题,直线与坐标轴的交点问题,平移的性质以及等腰三角形与一次函数的综合.利用数形结合和分类讨论的思想是解题关键.
23.(1)每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元.
(2)“玉兔灯笼”购进个,所获得的利润最大,最大利润为元.
【分析】(1)设每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元,再根据10个“玉兔灯笼”和15个“玉兔摆件”的售价为2400元;30个“玉兔灯笼”和20个“玉兔摆件”的售价为5200元,建立方程组,可得答案;
(2)设当月销售利润为元,“玉兔灯笼”购进个,则“玉兔摆件”购进个,再根据总利润等于两种商品的利润之和建立一次函数关系式,再根据一次函数的性质解决问题即可.
【详解】(1)解:设每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元,则
,解得:,
答:每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元.
(2)设当月销售利润为元,“玉兔灯笼”购进个,则“玉兔摆件”购进个,
∴
,
又∵,
解得:,
∵,
∴随的增大而减小,
∴当时,取得最大值,
此时;
∴“玉兔灯笼”购进个,所获得的利润最大,最大利润为元.
【点睛】本题考查的是二元一次方程组的应用,一元一次不等式组的应用,一次函数的应用,确定相等关系与不等关系建立方程,函数关系式或不等式组是解本题的关键.
24.()(为整数,且);()购门票共花了元.
【详解】(1)当时,y=10(x 20)+20×25=10x+300(其中x是整数);
(2)当x=54时,y=10x+300=840(元),
答:购门票共花了840元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
14.7一次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.宾馆有100间相同的客房,经过一段时间的经营,发现客房定价与客房的入住率之间有下表所示的关系,按照这个关系,要使客房的收入最高,每间客房的定价应为( )
每间房价(元)
入住率
A.300元 B.280元 C.260元 D.220元
2.某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲,乙两仓库的快件数量(件)与时间(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A.9:15 B.9:20 C.9:25 D.9:30
3.商户小李以每件元的价格购进某商品若干件到市场去销售,销售金额元与销售量件的函数关系的图象如图所示,则降价后每件商品销售获得的利润为( )
A.元 B.元 C.元 D.元
4.某学校计划租用甲、乙两种客车送240名师生(其中学生233名、教师7名)集体外出活动,要求每辆客车上至少要有1名教师.甲、乙两种客车的载客量和租金如下表:
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金(单位:元/辆) 400 280
则最节省费用的租车方案是( )
A.租甲种车4辆,租乙种车2辆 B.租甲种车5辆,租乙种车1辆
C.租甲种车2辆,租乙种车5辆 D.租甲种车3辆,租乙种车4辆
5.在平面直角坐标系中,已知点A(4,0),B(2,0),若点C在一次函数y=x+2的图象上,且△ABC为直角三角形.则满足条件的点C有( )
A.1个 B.2个 C.3个 D.4个
6.乐乐超市购进一批拼装玩具,进价为每个15元,在销售过程中发现,日销售量(个)与销售单价(元)之间满足如图所示的一次函数关系,若该玩具某天的销售单价是20元时,则当日的销售利润为( )
A.200元 B.300元 C.350元 D.500元
7.某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为张,购票总价为元).方案一:购票总价由图中的折线所表示的函数关系确定;方案二:提供元赞助后,每张票的票价为元.则两种方案购票总价相同时,的值为( )
A. B. C. D.
8.如图,直线与x轴、y轴分别交于A、B两点,点C为x的负半轴上的一点,连接,过点C作,与线段交于点D,若,则点D的坐标为( )
A. B. C. D.
9.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行米,先到终点的人原地休息.已知甲先出发分钟,在整个步行过程中,甲、乙两人的距离(米)与甲出发的时间(分)之间的关系如图所示,下列结论正确的是( )
A.甲步行的速度为米/分 B.乙走完全程用了分钟
C.乙用分钟追上甲 D.乙到达终点时,甲离终点还有米
10.如图所示,直线l1:yx+6与直线l2:yx﹣2交于点P(﹣2,3),不等式x+6x﹣2的解集是( )
A.x>﹣2 B.x≥﹣2 C.x<﹣2 D.x≤﹣2
11.如图,是某水果店销售某种水果的付款金额(元)与购买量之间的函数图象,李阳和王辉同学打算一起去该水果店分别购买这种水果,若他们合起来一次购买这种水果,则一共可节省( )
A.6元 B.5元 C.4元 D.3元
12.如图所示,已知点,一次函数的图象与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则的最小值是( )
A.4 B.5 C. D.
二、填空题
13.已知一次函数的图象与轴,轴分别交于点,.以为边在第一象限内作三角形,且,,作的中垂线交直线于点,交轴于点G.设上有一点,且点与点位于直线的同侧,使得,则点的坐标为 .
14.有甲乙两个长方体的蓄水池,将甲池中的水以每小时立方米的速度注入乙池,甲乙两个蓄水池中水的深度(米)与注水时间(小时)之间的函数图像如图所示,若要使甲乙两个蓄水池的蓄水量(指蓄水的体积)相同,则注水的时间应为
15.观察下表,知方程的解是 .
16.如图,购买一种商品,付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次性购买50千克这种商品要付款 元.
17.一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始内只进水不出水,从第到第内既进水又出水,从第开始只出水不进水,容器内水量(单位:)与时间(单位:)之间的关系如图所示,则图中的值是 .
三、解答题
18.某便利店老板购进了A,B两种口罩各100包供甲、乙两个便利店进行销售,预计两个店每包口罩的利润(单位:元)如下表:
A种口罩 B种口罩
甲店 a b
乙店 0.8 1
(1)若甲店销售A种口罩30包,B种口罩40包,可以盈利86元;销售A种口罩20包,B种口罩60包,可以盈利104元,求甲店这两种口罩每包的利润各是多少元.
(2)若甲、乙两个便利店各配货100包口罩,且保证乙店总利润不小于92元的条件下,请你设计出使便利店老板盈利最大的配货方案,并求出最大利润.
19.某空调厂的装配车间原计划用2个月时间(每月以30天计算),每天组装150台空调.
(1)从组装空调开始,组装的台数(单位:台/天)与生产的时间(单位:天)之间有怎样的函数关系?
(2)由于气温提前升高、厂家决定这批空调提前十天上市,那么装配车间每天至少要组装多少空调?
20.如图,∠MBN的两边BM,BN上分别有两点A、C,满足BC=2BA,作□ABCD,取AD的中点E,作CF⊥CD,CF与AB所在的直线交于点F.
(1)当∠B=时,直接写出∠DEF的度数;
(2)在射线BM绕B点旋转的过程中,若∠B=,∠DEF=(<X<,<Y<),求:Y关于X的函数解析式及相应自变量X的取值范围,
21.为了丰富同学们的课余生活,经市场了解,发现篮球的单价比足球的单价多元,用元购买的篮球的个数等于用元购买的足球的个数.
(1)求篮球和足球的单价
(2)为了支持学校开展体育活动,某校准备购买足球、篮球共个,且保证购买篮球数量不少于足球的一半,商店对篮球及足球进行打折销售,其中篮球打八折,足球打九折,请你给该校设计一个最省钱的购买方案,并求出最少费用为多少元?
22.如图所示,平面直角坐标系中,直线l1:y=﹣2x+3与直线l2:y=x+1相交于点A,直线l2与x轴相交于点B.过直线l2上的一点P(a,﹣1)作y轴的垂线,交直线l1于点C,连接BC.
(1)求点A的坐标;
(2)求△ABC的面积;
(3)将直线l1向下平移4个单位长度得到直线l3,设直线l3与y轴相交于点D,则直线l2上是否存在一点Q,使得△DPQ是以DP为腰的等腰三角形?若存在,请直接写出Q的坐标,若不存在,请说明理由.
23.为了迎接兔年的到来,广大市民纷纷开始购买兔年装饰物,某网店上架了“玉兔灯笼”和“玉兔摆件”这两款产品,已知10个“玉兔灯笼”和15个“玉兔摆件”的售价为2400元;30个“玉兔灯笼”和20个“玉兔摆件”的售价为5200元.
(1)每个“玉兔灯笼”和“玉兔摆件”的售价分别为多少元?
(2)已知“玉兔灯笼”和“玉兔摆件”的成本分别为80元/个和50元/个.进入2023年一月后,这两款产品持续热销,于是网店再购进了这两款产品共600个,其中“玉兔摆件”的数量不超过“玉兔灯笼”数量的2倍,且购进总价不超过37800元.为回馈新老客户,网店决定对“玉兔灯笼”降价10%后再销售,若一月份购进的这两款产品全部售出,则“玉兔灯笼”购进多少个时该网店当月销售利润最大?最大利润为多少?
24.“十一”黄金周期间,欢欢一家随旅游团到某风景区旅游,集体门票的收费标准是:人以内(含 人),每人元;超过人的,超过的部分每人元.
()写出应收门票费(元)与游览人数(人)(其中)之间的关系式.
()利用()中的关系式计算:若欢欢一家所在的旅游团共人,那么该旅游团购门票共花了多少钱?
《14.7一次函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C A D B D D A A
题号 11 12
答案 A C
1.C
【详解】当每间客房的定价为300元时,客房的收入为100×65%×300=19500(元);
当每间客房的定价为280元时,客房的收入为100×75%×280=21000(元);
当每间客房的定价为260元时,客房的收入为100×85%×260=22100(元);
当每间客房的定价为220元时,客房的收入为100×95%×220=20900(元).
所以当每间客房的定价为260元时,客房的收入最高.故选C.
2.B
【分析】分别求出甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数关系式,求出两条直线的交点坐标即可.
【详解】设甲仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y1=k1x+40,根据题意得60k1+40=400,解得k1=6,
∴y1=6x+40;
设乙仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y2=k2x+240,根据题意得60k2+240=0,解得k2=-4,
∴y2=-4x+240,
联立,解得,
∴此刻的时间为9:20.
故选B.
【点睛】本题考查了一次函数的应用,解题的关键:(1)熟练运用待定系数法就解析式;(2)解决该类问题应结合图形,理解图形中点的坐标代表的意义.
3.C
【分析】本题考查一次函数的利润问题.先根据图象得到降价后的售价,然后利用公式计算利润率即可.
【详解】解:∵由图象可知件销售金额为元,件的销售金额为元,
∴降价后卖了件,销售金额为元,
∴降价后每件商品销售的价格为元,
∴降价后每件商品的销售利润为元,
故选:C.
4.A
【分析】设租用甲客车x辆,租车总费用y元,由每辆客车上至少要有1名教师可知客车总数不能大于7辆,要保证240名师生有车坐,客车总数不能小于,客车总数不能小于6,可得客车总数为6,,根据题意列出一次函数和一元一次不等式,找到x的取值范围,再结合一次函数的增减性即可求解.
【详解】解:设租用甲客车x辆,租车总费用y元,由每辆客车上至少要有1名教师可知客车总数不能大于7辆,
要保证240名师生有车坐,客车总数不能小于,客车总数不能小于6,
∴客车总数为6,,
由题意可得,,
整理可得,
由题意,,
解得,
∵,
∴,
∵中,,y随x的增大而增大,
∴x取最小值时,即,y有最小值,
即当租甲种车4辆,租乙种车2辆,费用最少,
故选:A.
【点睛】本题考查一次函数和一元一次不等式的实际应用,利用题中的不等关系找到x的取值范围是解题的关键.
5.D
【详解】由题意知,直线y= x+2,与x轴的交点为(4,0),与y轴的交点为
(0,2),如图:
过点A作垂线与直线的交点W(-4,4),
过点B作垂线与直线的交点S(2,1),
过AB中点E(-1,0),作垂线与直线的交点为F(-1,2.5),
则EF=2.5<3,
所以以3为半径,以点E为圆心的圆与直线必有两个交点
∴共有四个点能与点A,点B组成直角三角形.
故选D.
6.B
【分析】根据题意,利用待定系数法求出与的一次函数关系式,然后将代入即可求出销售量,最后利用销售收入减去成本支出即可求出销售利润.
【详解】解:设与的一次函数关系式为,
由图可得,
解得,
所以与的一次函数关系式为,
把代入可得,
所以销售利润为(元).
故选B.
【点睛】本题考查求一次函数的关系式和利润问题,熟练掌握待定系数法求一次函数的关系式是解题的关键.
7.D
【分析】分别求出方案一中的OA和AB表示的解析式以及方案二的解析式,再进行比较即可得到结论.
【详解】解:在方案一中,设OA表示的解析式为,且
解得,
表示的解析式为:;
设表示的解析式为,
又,
解得,,
表示的解析式为:;
方案二的解析式为:;
当时,
故的图象与的图象无交点,
当时,,
所以,当时,两种方案购票总价相同.
故选:D.
【点睛】此题主要考查了一次函数的应用,运用待定系数法求一次函数关系式是解答本题的关键.
8.D
【分析】本题主要考查一次函数与几何综合,由直线求出点坐标,得出,过点D作于点E,证明,得,设点,则,得出,代入,求出的值即可.
【详解】解:对于,当时,,
∴,
∴,
过点D作于点E,如图,
则
∴,
∵,
∴
∴
∴,
又
∴,
∴,
设点,则,
∴,
把代入,得,
解得,,
∴,
故选:D.
9.A
【分析】根据题意和函数图象中的数据可以判断各个小题中的结论是否正确,从而可以解答本题.
【详解】由图可得,
甲步行的速度为:米/分,故正确,
乙走完全程用的时间为:(分钟),故错误,
乙追上甲用的时间为:(分钟),故错误,
乙到达终点时,甲离终点距离是:米,故错误,
故选.
【点睛】本题主要考查一次函数的实际应用、函数的图象,能从函数的图象中获取相关信息解决问题是解答的关键.
10.A
【分析】利用函数图象写出直线l1:y=x+6与在直线l2:y=-x-2上方所对应的自变量的范围即可.
【详解】当x>﹣2时,x+6x﹣2,
所以不等式x+6x﹣2的解集是x>﹣2.
故选A.
【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
11.A
【分析】本题考查了一次函数的应用.根据题意求出时与之间的函数关系式,再把代入计算可得答案.
【详解】解:当时,设与之间的函数关系式为,根据题意得:
,
解得,
,
当时,(元),
由图象可知,单独购买这种水果需要20元,
(元),
即若他们合起来一次购买这种水果,则一共可节省6元.
故选:A.
12.C
【分析】如图,点N关于OB的对称点N′(-1,0),过点N′作N′P⊥AB交OB于M,则PN′=PM+MN的最小值,根据直线AB的解析式为y=-x+4,得到直线N′P的解析式为y=x+1,得到,推出△PAN′是等腰直角三角形,于是得到结论.
【详解】解:如图,点N关于OB的对称点N′(-1,0),过点N′作N′P⊥AB交OB于M,
则PN′=PM+MN的最小值,
∵直线AB的解析式为y=-x+4,
∴A(4,0),B(0,4),
∴直线N′P的解析式为y=x+1,
由 解得
,
∵A(4,0),B(0,4),
∴OA=OB,
∴∠BAO=45°,
∴△PAN′是等腰直角三角形,
∵AN′=4+1=5,
∴
∴PM+MN的最小值是
故选:C
【点睛】本题考查一次函数的应用,等腰三角形的判定和性质等知识,解题的关键是利用对称性找到点M、点P位置,属于中考常考题型.
13.
【分析】先求出、两点的坐标,根据是的中垂线,则点,当时,,即点,故可得出的长;设,求出的面积,由,得到,即可求解;
【详解】解:如图,
是的中垂线,
点,
当时,即,
设
解得:
故答案为:.
【点睛】本题考查的是一次函数图象上点的坐标特点,涉及到三角形全等、中垂线的性质、勾股定理的运用,正确作出辅助线是解题的关键.
14.小时
【分析】本题考查用一次函数解决实际问题,先根据图像分别求出甲、乙两个蓄水池中水的深度与注水时间之间的函数关系式;设甲蓄水池的底面积为,乙蓄水池的底面积为,小时甲乙两个蓄水池的蓄水量相同,列出方程解答即可.正确理解题意并建立方程是解题的关键.
【详解】解:设,过点,,
得:,
解得:,
∴,
设,过点,,
得:,
解得:,
∴,
设甲蓄水池的底面积为,乙蓄水池的底面积为,小时甲乙两个蓄水池的蓄水量相同,
∵甲乙两个长方体的蓄水池,将甲池中的水以每小时立方米的速度注入乙池,甲水深度下降米,而乙水池深度升高米,
∴,,
∴,,
∴,即,
解得:,
∴注水小时甲、乙两个蓄水池的蓄水量相同.
故答案为:小时.
15.
【分析】设,要求方程的解,就是求函数当y=2450时对应的x的值,观察表格即可得出.
【详解】解:设,由题中所给表格,可知当时,,所以方程的解是.
【点睛】本题考查了一次函数与一元一次方程的关系,本题重在理解,即要求方程的解,就是求函数当y=2450时对应的x的值,前者是从数的角度,后者是从形的角度,数形结合,相得益彰.
16.420
【分析】当x>10时,用待定系数法求函数解析式即可.
【详解】解:当x>10时,付款金额y(元)与购买量x(千克)之间的函数为y=kx+b(k≠0),
∵图象过点(10,100)和(20,180),
∴,
解得:,
∴y与x的函数解析式为y=8x+20,
∴当x=50时,y=8×50+20=420,
一次性购买50千克这种商品要付款420元.
故答案为:420.
【点睛】本题考查一次函数的应用,解答本题的关键是求出射线AB段的函数解析式.
17.
【分析】根据图像可求出每分钟的进水量和出水量,运用待定系数求出直线的解析式,可求出时间为时容器中的水量,再根据从第开始只出水不进水,由此即可求解.
【详解】解:如图所示,
,,
∴每分钟的进水量为,即每分钟进水,
,,设每分钟出水量为,
∴,解得,,即每分钟出水量为,
设所在直线的解析式为,,,
∴,解得,,
∴直线的解析式为,
∵点在直线的图像上,且点的横坐标为,
∴,即,
∴当时,容器内水量,且每分钟出水量为,
根据题意得,,解得,,
故答案为:.
【点睛】本题主要考查一次函数图像与实际问题的综合运用,理解图像,掌握待定系数法求一次函数解析式是解题的关键.
18.(1)甲店A种口罩每包的利润是1元,B种口罩每包的利润是1.4元
(2)使便利店老板盈利最大的配货方案是:给甲店配送A种口罩60包.B种口罩40包.给乙店配送A种口罩40包,B种口罩60包,最大利润是208元
【分析】(1)根据题意,列出方程组求解即可.
(2)设给甲店配送A种口罩x包,B种口罩包,给乙店配送A种口罩包、B种口罩x包,两店总利润为W元.建立不等式求解即可.
【详解】(1)由题意,可列方程组,
解得
答:甲店A种口罩每包的利润是1元,B种口罩每包的利润是1.4元.
(2)设给甲店配送A种口罩x包,B种口罩包,给乙店配送A种口罩包、B种口罩x包,两店总利润为W元.
∵乙店总利润不小于92元,
∴,解得.
由题意,得.
∵.
∴W随x的增大而减小.
∴当时,W有最大值..
∴使便利店老板盈利最大的配货方案是:给甲店配送A种口罩60包.B种口罩40包.给乙店配送A种口罩40包,B种口罩60包,最大利润是208元.
【点睛】本题考查了方程组得应用,一次函数的应用,不等式的应用,熟练掌握方程组得解法,一次函数的应用是解题的关键.
19.(1),
(2)
【分析】本题考查了一元一次方程的应用,抓住全部装配的台数不变,建立等量关系.
(1)组装的台数等于每天组装的台数与天数的乘积;
(2)全部装配的台数不变,即台,而时间提前了10天,用时间装配速度全部装配的台数,建立方程.
【详解】(1)解:,;
(2)解:设装配车间每天至少要组装台空调,
依题意列方程:,
解得:.
答:装配车间每天至少要组装180台空调.
20.(1)∠DEF=135°°(2)当0°<∠B<60°时,y=90+x;当60°<∠B<180°时,y=270-x.
【详解】试题分析:(1) 当∠B=90°时, ABCD是矩形,则点F与点B重合,根据BC=2BA,点E是AD的中点,可得:AB=AE,所以∠ABE=∠AEB=45°,继而可得:∠DEF=180°-∠AEB=135°,
(2)对∠B的大小分三种情况讨论: ①当时,点F在线段AB上,,
②当时, 与①同理可得, ③当,F在线段BA的延长线上, y=.
试题解析:(1) 在 ABCD中,AD=BC,
当∠B=90°时, ABCD是矩形,则点F与点B重合,
∵BC=2BA,点E是AD的中点,
∴AB=AE,
∴∠ABE=∠AEB=45°,
∴∠DEF=180°-∠AEB=135°,即∠DEF=135°,
(2)对∠B的大小分三种情况讨论如下:
当时,点F在线段AB上(见图7-1),
延长FE,并与CD的延长线交于点G,记∠AFE=.
∵ ABCD,
∴ AB∥CD,AD=BC,AB=CD,∠3=∠B=x°,
∴ ∠DGE=∠AFE=,
可得 △AEF≌△DEG,
∴ EF=EG,CE为Rt△CFG斜边的中线,
∴ EF=EG,∠1=∠G=,
∵ BC=2AB,
∴ 2DE=2CD,DE=CD,
∴ 等腰三角形△CDE中,∠1==,
∴∠DEF=,
1>当∠B=90°时,F与点B重合,见图7-2) 此时∠DEF=135°,
所以仍成立,
2>当∠B=60°时,F与点A重合, ∠DEF=180°不合题意(见图7-3),
当时,F在线段AB的延长线上(见图7-4),
与①同理可得,
当,F在线段BA的延长线上(如图7-5),
与①同理可得CE为Rt△CFG斜边的中线,EC=EG,DE=CD,
∴ △CEG和△CDE为等腰三角形,
在等腰三角形△CEG中,∠1=180°-2∠2,在等腰三角形△CDE中,
,
∴ ∠DEF=180°-∠3=180°-(∠CED-∠1)=360°-3∠2=,
综上所述,当时,y=,
当时,.
21.(1)篮球的单价是,足球的单价是;
(2)最省钱的购买方案是:足球买个,篮球个,费用为.
【分析】(1)设足球的单价为x元,根据元购买的篮球的个数等于用元购买的足球的个数列方程即可得到答案;
(2)根据篮球数量不少于足球的一半列不等式,根据题意列出费用函数,根据函数性质即可得到最少方案.
【详解】(1)解:设足球的单价为x元,则篮球单价为元,由题意可得,
,
解得:,
∴,
∴篮球的单价是,足球的单价是;
(2)解:设购买足球m个,则篮球个,由题意可得,
且m为非负整数,
解得:的非负整数,
设费用为w,则有:
,
∵,
∴w随m增大而减小,
∴当时w最小,
最少费用为:,
∴最省钱的购买方案是:足球买个,篮球个,费用为.
【点睛】本题考查了分式方程的应用,一元一次不等式的应用,一次函数的性质,理解题意并根据题意求出函数关系式是解题的关键.
22.(1)
(2)
(3)存在,点Q坐标为:(﹣2,﹣1)或(﹣﹣2,﹣﹣1)或(0,1)
【分析】(1)联立方程组即可求解;
(2)分别求出点B,点P,点C坐标,再根据结合三角形的面积公式即可求解;
(3)先求出点D坐标,由等腰三角形的性质和两点之间的距离公式可求解.
【详解】(1)联立,
解得:,
∴点A(,);
(2)对于直线l2:,令,得:
解得:,
∴点B(-1,0).
∵点P(a,-1)在直线l2上,
∴-1=a+1,
解得:a=-2,
∴点P(-2,-1),
∴点C的纵坐标为-1.
对于直线l1:,当时,,
解得:x=2,
∴点C(2,-1),
∴
.
(3)存在,理由如下:
∵将直线l1向下平移4个单位长度得到直线l3,
∴直线l3的解析式为:,
∴点D(0,-1),
如图,
∵点P(-2,-1),点D(0,-1),
∴PD⊥y轴,PD=2,
设点Q(a,a+1),
∵△DPQ是以DP为腰的等腰三角形,
∴PQ=PD=2或PD=QD=2,
当PQ=PD=2时,则,
∴ ,
∴Q(,)或(,);
当PD=QD=2时,则,
∴a=0或-2(不合题意舍去),
∴Q(0,1),
综上所述:点Q坐标为:(,)或(,)或(0,1).
【点睛】本题为一次函数综合题.考查两直线的交点问题,直线与坐标轴的交点问题,平移的性质以及等腰三角形与一次函数的综合.利用数形结合和分类讨论的思想是解题关键.
23.(1)每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元.
(2)“玉兔灯笼”购进个,所获得的利润最大,最大利润为元.
【分析】(1)设每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元,再根据10个“玉兔灯笼”和15个“玉兔摆件”的售价为2400元;30个“玉兔灯笼”和20个“玉兔摆件”的售价为5200元,建立方程组,可得答案;
(2)设当月销售利润为元,“玉兔灯笼”购进个,则“玉兔摆件”购进个,再根据总利润等于两种商品的利润之和建立一次函数关系式,再根据一次函数的性质解决问题即可.
【详解】(1)解:设每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元,则
,解得:,
答:每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元.
(2)设当月销售利润为元,“玉兔灯笼”购进个,则“玉兔摆件”购进个,
∴
,
又∵,
解得:,
∵,
∴随的增大而减小,
∴当时,取得最大值,
此时;
∴“玉兔灯笼”购进个,所获得的利润最大,最大利润为元.
【点睛】本题考查的是二元一次方程组的应用,一元一次不等式组的应用,一次函数的应用,确定相等关系与不等关系建立方程,函数关系式或不等式组是解本题的关键.
24.()(为整数,且);()购门票共花了元.
【详解】(1)当时,y=10(x 20)+20×25=10x+300(其中x是整数);
(2)当x=54时,y=10x+300=840(元),
答:购门票共花了840元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
