15.5三角形中位线定理巩固强化练习(含解析)
文档属性
| 名称 | 15.5三角形中位线定理巩固强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
15.5三角形中位线定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在平行四边形中,,,点H、G分别是边上的动点.连接,点E为的中点,点F为的中点,连接.则的最大值与最小值的差为( )
A.1 B. C. D.
2.已知△ABC的各边长度分别为3cm,4cm,5cm,则连接各边中点的三角形的周长为( )
A.2cm B.7cm C.5cm D.6cm
3.如图,的对角线,相交于点,的平分线与边相交于点,是的中点,若,,则的长为( )
A. B. C. D.
4.如图,在四边形中,,点E、F、G、H分别是边、、、的中点,四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
5.如图,点D、E、F分别为∠ABC三边的中点,若△DEF的周长为10,则△ABC的周长为【 】
A.5 B.10 C.20 D.40
6.如图所示,在中,,,D是边的中点,E是边上一点,若平分的周长,则的长是( )
A.1 B.2 C. D.
7.如图,ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为( )
A. B.1 C. D.7
8.如图, ABCD中,对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,BC=2AB=4,则下列结论:①AD=4OE;②BD=2;③30°<∠BOE<45°;④S△AOP=.其中正确的个数是( )
A.4 B.3 C.2 D.1
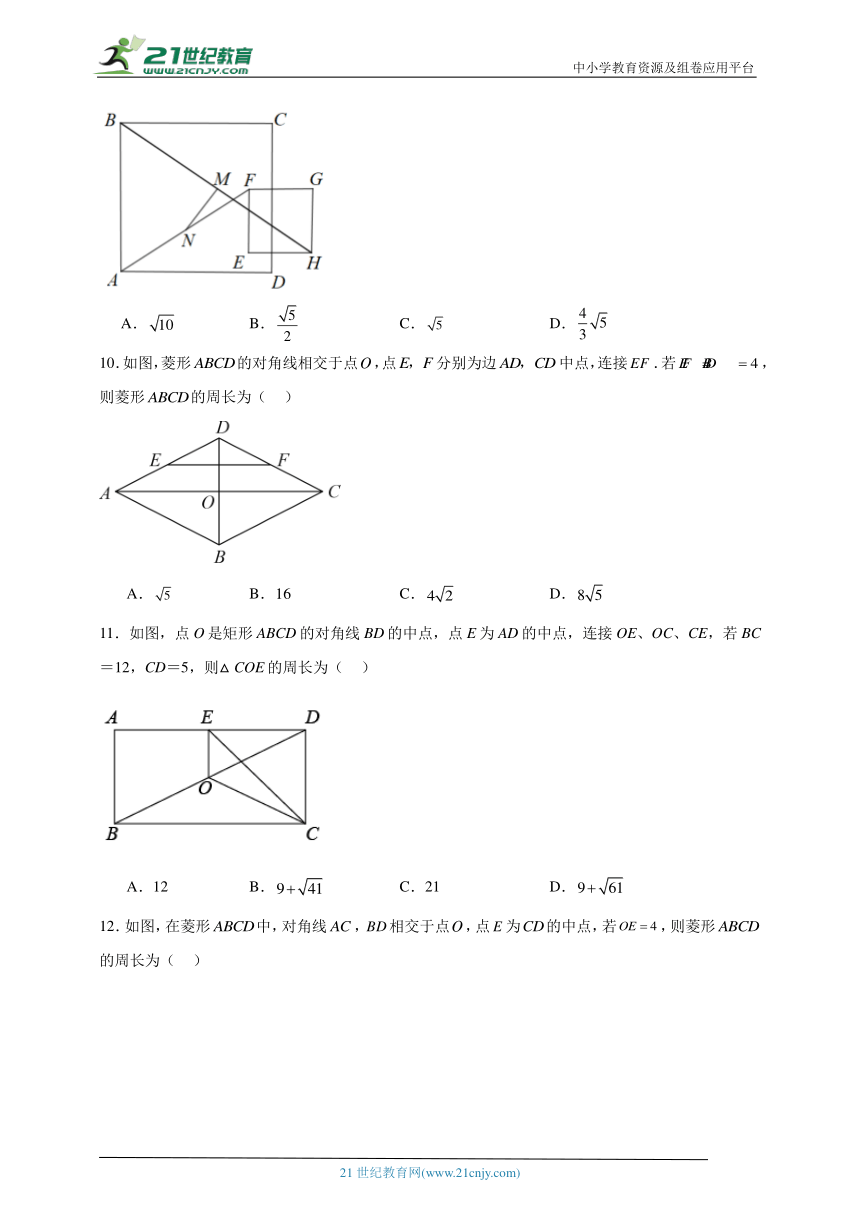
9.如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上平移,在平移过程中,始终保持EF∥AB,线段BH的中点为M,AF的中点为N,则线段MN的长为( )
A. B. C. D.
10.如图,菱形的对角线相交于点,点分别为边中点,连接.若,则菱形的周长为( )
A. B. C. D.
11.如图,点O是矩形ABCD的对角线BD的中点,点E为AD的中点,连接OE、OC、CE,若BC=12,CD=5,则△COE的周长为( )
A.12 B. C.21 D.
12.如图,在菱形中,对角线,相交于点,点为的中点,若,则菱形的周长为( )
A.48 B.32 C.24 D.16
二、填空题
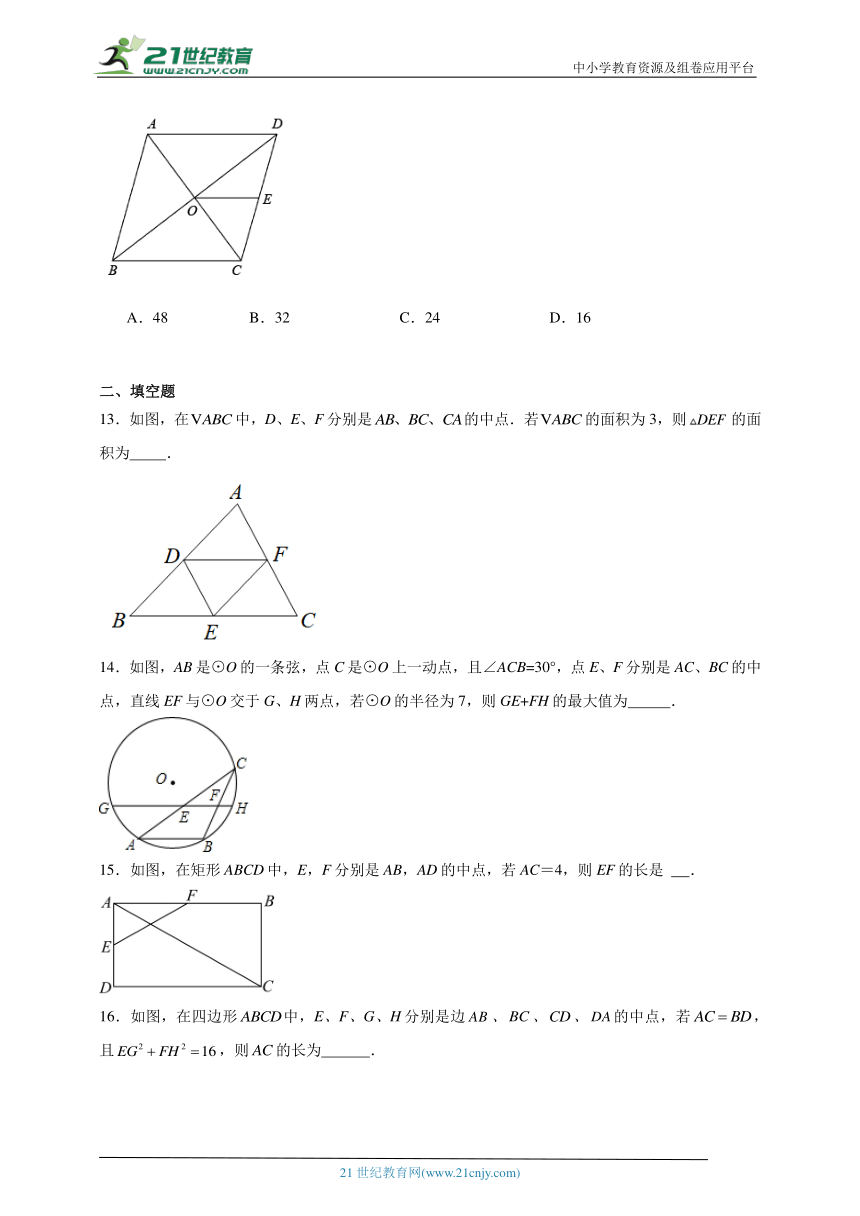
13.如图,在中,D、E、F分别是的中点.若的面积为3,则的面积为 .
14.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的最大值为 .
15.如图,在矩形ABCD中,E,F分别是AB,AD的中点,若AC=4,则EF的长是 .
16.如图,在四边形中,E、F、G、H分别是边、、、的中点,若,且,则的长为 .
17.如图,在中,点,分别是边,的中点,点是线段上的一点.连接,,,且,,则的长是 .
三、解答题
18.取任意一张三角形纸片,你能把它剪成四个全等的三角形吗?说明你的方法,并画出示意图.
19.如图,在△ABC中,AB=AC,AE是∠BAC的角平分线,点O为AB的中点,延长EO交△ABC的外角平分线于点F.
(1)求证:EO=OF;
(2)连接BF,试判断四边形AEBF的形状,并证明你的结论.
20.如图,图1中ΔABC是等边三角形,DE是中位线,F是线段BC延长线上一点,且CF=AE,连接BE,EF.
(1)求证:BE=EF;
(2)若将DE从中位线的位置向上平移,使点D、E分别在线段AB、AC上(点E与点A不重合),其他条件不变,如图2,则(1)题中的结论是否成立?若成立,请证明;若不成立.请说明理由.
21.如图所示,已知四边形,,点F在的延长线上,连接交于E,E刚好为的中点.
(1)求证:;
(2)若点B为线段的中点,且,求的长.
22.如图,、分别是不等边三角形(即)的边、的中点,是内的动点,连接、,点、分别是、的中点,顺次连接点、、、.
(1)求证:四边形是平行四边形;
(2)若四边形是菱形,则与应满足怎样的数量关系?并说明理由.
23.如图,是的中位线,点为射线上的一个动点(不与点E重合),作交边于点,连结.
(1)如图1,当点M与点D重合时,求证:四边形是平行四边形;
(2)如图,当四边形是菱形时,,求菱形的面积;
(3)如图3,,在延长线上(可以与点D重合),使得四边形为矩形,求的度数范围.
24.已知:如图,在中,∠BAC=90°,DE、DF是 的中位线,连接EF、AD.求证:EF=AD.
《15.5三角形中位线定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D C C D A A C D
题号 11 12
答案 D B
1.C
【分析】本题考查平行四边形的性质、三角形的中位线定理、等边三角形的判定和性质、直角三角形30度角性质、垂线段最短等知识,解题的关键是学会添加常用辅助线,本题的突破点是证明,属于中考选择题中的压轴题.如图,取的中点M,连接,作于N.首先证明,求出,利用三角形中位线定理,可知,求出的最大值以及最小值即可解决问题.
【详解】解:如图,取的中点M,连接,作于N.
∵四边形是平行四边形,,
∴,
∵,
∴是等边三角形,
∴,
∴,
∴,
∴,
在中,
∵,
∴,
∵,
∴,
易知的最大值为的长,最小值为的长,
∴的最大值为,最小值为,
∴的最大值为,最小值为,
∴的最大值与最小值的差为.
故选:C.
2.D
【详解】如图,D,E,F分别是△ABC的三边的中点,
则DE=AC,DF=BC,EF=AB,
∴△DEF的周长=DE+DF+EF=(AC+BC+AB)=6cm,
故选D.
3.D
【分析】本题考查了平行四边形的性质,等角对等边,三角形中位线性质;熟练掌握这些知识是关键.由平行四边形的性质及角平分线的定义得,从而得的长,由三角形中位线定理即可求解.
【详解】解:在中,,,,
;
平分,
,
,
;
;
E是的中点,,
;
故选:D.
4.C
【分析】本题考查了菱形的判定以及三角形的中位线定理,顺次连接任意四边形四边中点所得的四边形,一组对边平行并且等于原来四边形某一对角线的一半,说明新四边形的对边平行且相等.所以是平行四边形,再根据即可证明结论.
【详解】解:∵点E、F、G、H分别是边、、、的中点,
∴,,,,,
且,
四边形是平行四边形,
∵,
∴,
∴四边形为菱形.
故选:C.
5.C
【详解】由已知,点D、E、F分别为∠ABC三边的中点,根据三角形中位线定理,得AB、BC、AC分别是FE、DF、DE的两倍.因此,由△DEF的周长为10,得△ABC的周长为20.故选C.
6.D
【分析】延长到点F,使,连接AF,过点作于点H,根据DE平分的周长, D为中点,推出,得到,推出是的中位线.得到,,根据三角形外角性质和等边对等角,, =1,得到,推出,推出,得到.
【详解】延长到点F,使,连接AF,过点作于点H,
平分的周长,且D为中点
是的中位线.
,
, =1,
,
∴,
,
.
故选:D.
【点睛】本题主要考查了三角形中位线,等腰三角形,三角形外角,含30°角的直角三角形,解决问题的关键是添加辅助线,熟练掌握三角形中位线的判定和性质,等腰三角形性质,三角形外角性质,含30°角的直角三角形边的性质.
7.A
【分析】先证明△AGC是等腰三角形,再利用中线的性质计算即可;
【详解】解:∵AD是△ABC角平分线,CG⊥AD于F,
∴△AGC是等腰三角形,
∴AG=AC=3,GF=CF,
∵AB=4,AC=3,
∴BG=1,
∵AE是△ABC中线,
∴BE=CE,
∴EF为△CBG的中位线,
∴EF=BG=,
故选:A.
【点睛】本题主要考查了三角形角平分线和中线的性质,准确计算是解题的关键.
8.A
【分析】①先根据角平分线和平行线的性质得:∠BAE=∠BEA,则AB=BE=2,由有一个角是60度的等腰三角形是等边三角形得:△ABE是等边三角形,即可得到E为BC中点,再根据中位线定理得到AB=2OE,即AD=4OE ;②先根据三角形中位线定理得:OE=AB=1,OE∥AB,根据勾股定理计算OC,OD的长,即可求BD的长;③根据大角对大边进行计算求解即可得到答案;④过点P分别作PM⊥AB于M,PN⊥AD于N可以得到即可求得,由此求出即可得出结论.
【详解】解:∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC=60°,AD=BC,OA=OC,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE=2,
∴△ABE是等边三角形,
∴AE=BE=2,
∵BC=4,
∴EC=2,
∴AE=EC,
∴∠EAC=∠ACE,
∵∠AEB=∠EAC+∠ACE=60°,
∴∠ACE=30°,
∵AD∥BC,
∴∠CAD=∠ACE=30°,
∴∠BAC=∠DCA=90°,
∵CE=BE=2
∴E为BC的中点
∴OE为△ABC的中位线
∴OE=AB=1,OE∥AB,
∴∠EOC=∠BAC=90°,
∵BC=2AB
∴BC=4OE
∴AD=4OE
∴①正确
Rt△EOC中,OC=,
在Rt△OCD中,OD=
BD=2OD=2
故②正确
在Rt△AOE中,∵AE是斜边
∴AE>AO
∴AB>AO
∴∠AOB>∠ABO
∴∠AOB>45°
∴∠BOE=90°-∠AOB<45°
∵OE=
∴∠BOE>∠OBE
∵∠ACB=30°,∠EOC=90°
∴∠OEC=60°
∴∠OEB=120°
∴∠BOE +∠OBE=60°
∴∠BOE>30°
∴③正确
过点P分别作PM⊥AB于M,PN⊥AD于N
∴PM=PN(角平分线的性质)
∴
∵四边形ABCD是平行四边形
∴
∴
∴
∴
∵四边形ABCD是平行四边形
∴AO=OC=,
∴
∴④正确
综上,正确的个数是4个
故选:A.
【点睛】本题考查了平行四边形的性质、等腰三角形的性质、直角三角形30度角的性质、三角形面积,角平分线的性质,三角形中位线定理,大角对大边等知识;熟练掌握平行四边形的性质,证明△ABE是等边三角形是解决问题的关键,并熟练掌握同高三角形面积的关系.
9.C
【分析】连接EM并延长交BC于点R,连接EN并延长交AB于点P,证明△BRM≌△HEM(AAS),推出RM=EM,BR=EH=2,同理可得△APN≌△FEN,推出PN=EN,AP=EF=2,勾股定理求出PR,根据三角形中位线的定义及性质求出MN.
【详解】解:如图,连接EM并延长交BC于点R,连接EN并延长交AB于点P,
∵正方形EFGH在正方形ABCD所在平面上平移,在平移过程中,始终保持EF∥AB,
∴BCEH,
∴∠RBM=∠EHM,∠BRM=∠HEM,
∵BM=MH,
∴△BRM≌△HEM(AAS),
∴RM=EM,BR=EH=2,
∵EFAB,
同理可得△APN≌△FEN,
∴PN=EN,AP=EF=2,
∴BP=AB-AP=6-2=4,
在Rt△BPR中,BP2+BR2=PR2,
∴42+22=PR2,
∴PR=2,
∵RM=EM,PN=EN,
∴MN是△PRE的中位线,
∴MN=PR=,
故选:C.
【点睛】此题考查了正方形及平移的性质,勾股定理,全等三角形的判定和性质,三角形中位线的定义和性质,正确理解题意并作出辅助线是解题的关键.
10.D
【分析】根据中位线的性质可求的长度,根据菱形的性质,勾股定理可求的长,由此即可求解.
【详解】解:∵点分别为边中点,
∴是的中位线,且,
∴,则,
∵四边形是菱形,
∴,,,
在中,,
∴菱形的周长为,
故选:.
【点睛】本题主要考查菱形的性质,中位线的性质,勾股定理的综合,掌握菱形的菱形,三角形中位线的性质,勾股定理求边长等知识的综合是解题的关键.
11.D
【分析】由勾股定理可求BD,由中位线,中线的性质求OE、EC,进而可求△COE的周长;
【详解】解:在矩形ABCD中,,
∴,
∵点O是BD的中点,
∴,
∵点E为AD的中点,
∴,,
∴,
∴△COE的周长为,
故选:D.
【点睛】本题主要考查勾股定理的应用、中位线的性质、中线的性质,掌握相关知识并灵活应用是解题的关键.
12.B
【分析】由菱形的性质先证明再求解 从而可得到答案.
【详解】解:菱形ABCD中,对角线相交于点O,E是的中点,
菱形ABCD的周长为
故选:B.
【点睛】本题考查的是菱形的性质,三角形的中位线的性质,掌握“三角形的中位线平行于第三边,并且等于第三边的一半”是解题的关键.
13./0.75
【分析】本题考查了三角形的中位线定理,平行四边形的判定与性质,掌握三角形的中位线定理是解题的关键.
由三角形的中位线定理得到,继而四边形均为平行四边形,则,即可求解.
【详解】解:∵D、E、F分别是的中点,
∴,
∴四边形均为平行四边形,
∴,
∴,
故答案为:.
14.10.5
【分析】将求GE+FH的最大值转化为GH-EF的值,因为EF是△ABC的中位线,EF=,AB的长度不变,所以只要GH的长最大即可,当GH为直径时,其长度最大.
【详解】如图,连接OA,OB,
∵∠ACB=30°,
∴∠AOB=60°.
∵OA=OB,
∴△OAB是等边三角形.
∴OA=OB=AB=7.
∵E、F是AC、BC的中点,
∴EF==3.5.
∵GE+FH=GH-EF,EF为定值,∴要使GE+FH最大,即要GH最大.
∴当GH为直径时,GE+FH的最大值为14-3.5=10.5.
【点睛】本题考查等边三角形的判定和三角形的中位线的性质.将求GE+FH的最大值转化为求GH-EF的最大值,是解题的关键.
15.2
【分析】连接BD,由矩形的性质可得AC=BD=4,由三角形的中位线定理可求解.
【详解】解:如图,连接BD,
∵四边形ABCD是矩形,
∴AC=BD=4,
∵E,F分别是AD,AB的中点,
∴EF=BD=2,
故答案为:2.
【点睛】本题考查了矩形的性质,三角形中位线定理,掌握矩形对角线相等是解题的关键.
16.4
【分析】本题主要考查了三角形中位线定理和菱形的判定方法,题目比较典型,又有综合性,难度较大.根据三角形的中位线定理和菱形的判定,可得顺次连接对角线相等的四边形各边中点所得四边形是菱形,根据菱形的性质得到,再由勾股定理得出的长,从而得到答案.
【详解】解:如图,设和相交于点O.
∵E、F、G、H分别是边,,,的中点,
∴分别是的中位线,分别是的中位线,
∴,
又∵,
∴,
∴四边形是菱形,
∴,
∴
,
∴.
故答案为:4.
17.3
【分析】根据三角形中位线定理和直角三角形的性质即可得到结论.
【详解】解:∵点D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∵BC=14,
∴DE=BC=7,
∵∠AFB=90°,AB=8,
∴DF=AB=4,
∴EF=DE-DF=7-4=3,
故答案为:3.
【点睛】本题考查了三角形中位线定理,直角三角形的性质,熟练掌握三角形中位线定理是解题的关键.
18.见解析
【分析】先取的三边的中点D、E、F,连接、、,即可得出答案.
【详解】解:如图,方法为:取的三边的中点D、E、F,连接、、,沿、、剪开,即可得出四个全等的三角形,
理由如下:
∵D,E,F分别为,,的中点,
∴,,,
∴,
∴,
同理可得:,
∴.
【点睛】本题考查了全等三角形的判定和三角形的中位线,能灵活运用定理进行推理是解此题的关键,通过此题培养了学生的思维能力和动手操作能力.
19.(1)见解析
(2)四边形AEBF是矩形,理由见解析
【分析】(1)由等腰三角形的性质可得CE=BE,∠AEB=90°,由三角形的中位线定理可得EO∥AC,由直角三角形的性质和平行线的性质可证OE=OF;
(2)由矩形的判定可得结论.
【详解】(1)证明:∵AB=AC,AE是∠BAC的角平分线,
∴CE=BE,∠AEB=90°,
∵点O是AB的中点,
∴EO是△ABC的中位线,EO=AO=BO,
∴EO∥AC,
∴∠EFA=∠FAD,
∵AF平分∠BAD,
∴∠FAD=∠FAB,
∴∠FAB=∠EFA,
∴OF=AO,
∴OE=OF;
(2)解:四边形AEBF是矩形,理由如下:
如图,
∵AO=BO,EO=FO,
∴四边形AEBF是平行四边形,
∵∠AEB=90°,
∴四边形AEBF是矩形.
【点睛】本题考查了矩形的判定,等腰三角形的性质,三角形中位线定理等知识,灵活运用这些性质解决问题是解题的关键.
20.(1)证明见解析;(2)结论仍然成立;(3)
【分析】(1)利用等边三角形的性质以及三线合一证明得出结论;
(2)由中位线的性质、平行线的性质,等边三角形的性质以及三角形全等的判定与性质证明
【详解】(1)证明:∵ΔABC是等边三角形,
∴∠ABC=∠ACB=,AB=BC=AC
∵DE是中位线,
∴E是AC的中点,
∴BE平分∠ABC,AE=EC
∴∠EBC=∠ABC=
∵AE=CF,
∴CE=CF,
∴∠CEF=∠F
∵∠CEF+∠F=∠ACB=,
∴∠F=,
∴∠EBC=∠F,
∴BE=EF
(2)结论仍然成立.
∵DE是由中位线平移所得;
∴DE//BC,
∴∠ADE=∠ABC=,∠AED=∠ACB=,
∴ΔADE是等边三角形,
∴DE=AD=AE,
∵AB=AC,
∴BD=CE,
∵AE=CF,
∴DE=CF
∵∠BDE=-∠ADE=,∠FCE=-∠ACB=,
∴∠FCE=∠EDB,
∴ΔBDE≌ΔECF,
∴BE=EF
【点睛】此题考查等边三角形的判定与性质,三角形中位线定理和全等三角形的判定与性质,解题关键在于利用三线合一证明得出结论
21.(1)见解析;
(2).
【分析】(1)利用平行线的性质,可得,即可求证;
(2)根据三角形中位线的性质,可得,由(1)可得,则
【详解】(1)证明:∵,
∴,
∵为的中点,
∴,
又∵,
∴;
(2)解:∵为的中点,点B为线段的中点,
∴为的中位线,,
∴,
由(1)得,
∴,即,
∴.
【点睛】此题考查了全等三角形的判定与性质,三角形中位线的性质,平行线的性质,解题的关键是熟练掌握相关基础性质.
22.(1)证明见解析
(2),理由见解析
【分析】(1)首先利用三角形中位线的性质得出,,,,从而得出,,即可证得四边形是平行四边形;
(2)由四边形是菱形,可得,再根据三角形中位线的性质可得,,从而得出.
【详解】(1)证明:∵D、E分别是边、的中点.
∴,,
∵点G、F分别是、的中点,
∴,,
∴四边形是平行四边形;
(2)解:,理由如下:
连接,
∵四边形是菱形,
∴,
∵D是的中点,点G、F分别是、的中点,
∴,,
∴.
【点睛】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,菱形的判定以及平行四边形与菱形的关系,熟记相关的定理和性质是解题的关键.
23.(1)见解析
(2)2
(3)
【分析】本题考查菱形的性质,平行四边形的判定和性质,中位线的性质等综合题型,解题的关键对菱形性质和图形变化极值情况的熟练掌握.
(1)根据平行四边形判定及性质进行证明即可;
(2)如图,连接,由菱形知,可证,四边形是平行四边形,于是,由勾股定理中,,所以菱形的面积即可求得;
(3)如图,点在延长线上(可以与点重合),得;随着的减小,点逐渐向点接近,当点与点重合时,最小,由矩形性质得,进一步证得,由三角形内角和定理,得,于是.
【详解】(1)证明:∵是的中位线,
∴是中点,
又,
∴四边形是平行四边形,
∴,
∵,
∴,且,
∴四边形是平行四边形,即四边形是平行四边形;
(2)解:如图2,连接,
∵四边形是菱形,
∴,
∴,
∵,
∴,
∵,
∴四边形是平行四边形,
∴,
在中,,
∴,
∵,
∴,
∴,
∴菱形的面积为2;
(3)解:如图,点在延长线上(可以与点重合),
∴,
随着的减小,点逐渐向点接近,当点与点重合时,最小,如图,四边形是矩形,
,
而,
,
,
,
.
24.见解析
【分析】由DE、DF是△ABC的中位线,得出DE∥AB,DF∥AC,进而证明四边形AEDF是平行四边形,再根据条件∠BAC=90°,证得平行四边形AEDF是矩形即可得出结论.
【详解】证明:∵DE,DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
又∵∠BAC=90°,
∴平行四边形AEDF是矩形,
∴EF=AD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
15.5三角形中位线定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在平行四边形中,,,点H、G分别是边上的动点.连接,点E为的中点,点F为的中点,连接.则的最大值与最小值的差为( )
A.1 B. C. D.
2.已知△ABC的各边长度分别为3cm,4cm,5cm,则连接各边中点的三角形的周长为( )
A.2cm B.7cm C.5cm D.6cm
3.如图,的对角线,相交于点,的平分线与边相交于点,是的中点,若,,则的长为( )
A. B. C. D.
4.如图,在四边形中,,点E、F、G、H分别是边、、、的中点,四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
5.如图,点D、E、F分别为∠ABC三边的中点,若△DEF的周长为10,则△ABC的周长为【 】
A.5 B.10 C.20 D.40
6.如图所示,在中,,,D是边的中点,E是边上一点,若平分的周长,则的长是( )
A.1 B.2 C. D.
7.如图,ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为( )
A. B.1 C. D.7
8.如图, ABCD中,对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,BC=2AB=4,则下列结论:①AD=4OE;②BD=2;③30°<∠BOE<45°;④S△AOP=.其中正确的个数是( )
A.4 B.3 C.2 D.1
9.如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上平移,在平移过程中,始终保持EF∥AB,线段BH的中点为M,AF的中点为N,则线段MN的长为( )
A. B. C. D.
10.如图,菱形的对角线相交于点,点分别为边中点,连接.若,则菱形的周长为( )
A. B. C. D.
11.如图,点O是矩形ABCD的对角线BD的中点,点E为AD的中点,连接OE、OC、CE,若BC=12,CD=5,则△COE的周长为( )
A.12 B. C.21 D.
12.如图,在菱形中,对角线,相交于点,点为的中点,若,则菱形的周长为( )
A.48 B.32 C.24 D.16
二、填空题
13.如图,在中,D、E、F分别是的中点.若的面积为3,则的面积为 .
14.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的最大值为 .
15.如图,在矩形ABCD中,E,F分别是AB,AD的中点,若AC=4,则EF的长是 .
16.如图,在四边形中,E、F、G、H分别是边、、、的中点,若,且,则的长为 .
17.如图,在中,点,分别是边,的中点,点是线段上的一点.连接,,,且,,则的长是 .
三、解答题
18.取任意一张三角形纸片,你能把它剪成四个全等的三角形吗?说明你的方法,并画出示意图.
19.如图,在△ABC中,AB=AC,AE是∠BAC的角平分线,点O为AB的中点,延长EO交△ABC的外角平分线于点F.
(1)求证:EO=OF;
(2)连接BF,试判断四边形AEBF的形状,并证明你的结论.
20.如图,图1中ΔABC是等边三角形,DE是中位线,F是线段BC延长线上一点,且CF=AE,连接BE,EF.
(1)求证:BE=EF;
(2)若将DE从中位线的位置向上平移,使点D、E分别在线段AB、AC上(点E与点A不重合),其他条件不变,如图2,则(1)题中的结论是否成立?若成立,请证明;若不成立.请说明理由.
21.如图所示,已知四边形,,点F在的延长线上,连接交于E,E刚好为的中点.
(1)求证:;
(2)若点B为线段的中点,且,求的长.
22.如图,、分别是不等边三角形(即)的边、的中点,是内的动点,连接、,点、分别是、的中点,顺次连接点、、、.
(1)求证:四边形是平行四边形;
(2)若四边形是菱形,则与应满足怎样的数量关系?并说明理由.
23.如图,是的中位线,点为射线上的一个动点(不与点E重合),作交边于点,连结.
(1)如图1,当点M与点D重合时,求证:四边形是平行四边形;
(2)如图,当四边形是菱形时,,求菱形的面积;
(3)如图3,,在延长线上(可以与点D重合),使得四边形为矩形,求的度数范围.
24.已知:如图,在中,∠BAC=90°,DE、DF是 的中位线,连接EF、AD.求证:EF=AD.
《15.5三角形中位线定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D C C D A A C D
题号 11 12
答案 D B
1.C
【分析】本题考查平行四边形的性质、三角形的中位线定理、等边三角形的判定和性质、直角三角形30度角性质、垂线段最短等知识,解题的关键是学会添加常用辅助线,本题的突破点是证明,属于中考选择题中的压轴题.如图,取的中点M,连接,作于N.首先证明,求出,利用三角形中位线定理,可知,求出的最大值以及最小值即可解决问题.
【详解】解:如图,取的中点M,连接,作于N.
∵四边形是平行四边形,,
∴,
∵,
∴是等边三角形,
∴,
∴,
∴,
∴,
在中,
∵,
∴,
∵,
∴,
易知的最大值为的长,最小值为的长,
∴的最大值为,最小值为,
∴的最大值为,最小值为,
∴的最大值与最小值的差为.
故选:C.
2.D
【详解】如图,D,E,F分别是△ABC的三边的中点,
则DE=AC,DF=BC,EF=AB,
∴△DEF的周长=DE+DF+EF=(AC+BC+AB)=6cm,
故选D.
3.D
【分析】本题考查了平行四边形的性质,等角对等边,三角形中位线性质;熟练掌握这些知识是关键.由平行四边形的性质及角平分线的定义得,从而得的长,由三角形中位线定理即可求解.
【详解】解:在中,,,,
;
平分,
,
,
;
;
E是的中点,,
;
故选:D.
4.C
【分析】本题考查了菱形的判定以及三角形的中位线定理,顺次连接任意四边形四边中点所得的四边形,一组对边平行并且等于原来四边形某一对角线的一半,说明新四边形的对边平行且相等.所以是平行四边形,再根据即可证明结论.
【详解】解:∵点E、F、G、H分别是边、、、的中点,
∴,,,,,
且,
四边形是平行四边形,
∵,
∴,
∴四边形为菱形.
故选:C.
5.C
【详解】由已知,点D、E、F分别为∠ABC三边的中点,根据三角形中位线定理,得AB、BC、AC分别是FE、DF、DE的两倍.因此,由△DEF的周长为10,得△ABC的周长为20.故选C.
6.D
【分析】延长到点F,使,连接AF,过点作于点H,根据DE平分的周长, D为中点,推出,得到,推出是的中位线.得到,,根据三角形外角性质和等边对等角,, =1,得到,推出,推出,得到.
【详解】延长到点F,使,连接AF,过点作于点H,
平分的周长,且D为中点
是的中位线.
,
, =1,
,
∴,
,
.
故选:D.
【点睛】本题主要考查了三角形中位线,等腰三角形,三角形外角,含30°角的直角三角形,解决问题的关键是添加辅助线,熟练掌握三角形中位线的判定和性质,等腰三角形性质,三角形外角性质,含30°角的直角三角形边的性质.
7.A
【分析】先证明△AGC是等腰三角形,再利用中线的性质计算即可;
【详解】解:∵AD是△ABC角平分线,CG⊥AD于F,
∴△AGC是等腰三角形,
∴AG=AC=3,GF=CF,
∵AB=4,AC=3,
∴BG=1,
∵AE是△ABC中线,
∴BE=CE,
∴EF为△CBG的中位线,
∴EF=BG=,
故选:A.
【点睛】本题主要考查了三角形角平分线和中线的性质,准确计算是解题的关键.
8.A
【分析】①先根据角平分线和平行线的性质得:∠BAE=∠BEA,则AB=BE=2,由有一个角是60度的等腰三角形是等边三角形得:△ABE是等边三角形,即可得到E为BC中点,再根据中位线定理得到AB=2OE,即AD=4OE ;②先根据三角形中位线定理得:OE=AB=1,OE∥AB,根据勾股定理计算OC,OD的长,即可求BD的长;③根据大角对大边进行计算求解即可得到答案;④过点P分别作PM⊥AB于M,PN⊥AD于N可以得到即可求得,由此求出即可得出结论.
【详解】解:∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC=60°,AD=BC,OA=OC,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE=2,
∴△ABE是等边三角形,
∴AE=BE=2,
∵BC=4,
∴EC=2,
∴AE=EC,
∴∠EAC=∠ACE,
∵∠AEB=∠EAC+∠ACE=60°,
∴∠ACE=30°,
∵AD∥BC,
∴∠CAD=∠ACE=30°,
∴∠BAC=∠DCA=90°,
∵CE=BE=2
∴E为BC的中点
∴OE为△ABC的中位线
∴OE=AB=1,OE∥AB,
∴∠EOC=∠BAC=90°,
∵BC=2AB
∴BC=4OE
∴AD=4OE
∴①正确
Rt△EOC中,OC=,
在Rt△OCD中,OD=
BD=2OD=2
故②正确
在Rt△AOE中,∵AE是斜边
∴AE>AO
∴AB>AO
∴∠AOB>∠ABO
∴∠AOB>45°
∴∠BOE=90°-∠AOB<45°
∵OE=
∴∠BOE>∠OBE
∵∠ACB=30°,∠EOC=90°
∴∠OEC=60°
∴∠OEB=120°
∴∠BOE +∠OBE=60°
∴∠BOE>30°
∴③正确
过点P分别作PM⊥AB于M,PN⊥AD于N
∴PM=PN(角平分线的性质)
∴
∵四边形ABCD是平行四边形
∴
∴
∴
∴
∵四边形ABCD是平行四边形
∴AO=OC=,
∴
∴④正确
综上,正确的个数是4个
故选:A.
【点睛】本题考查了平行四边形的性质、等腰三角形的性质、直角三角形30度角的性质、三角形面积,角平分线的性质,三角形中位线定理,大角对大边等知识;熟练掌握平行四边形的性质,证明△ABE是等边三角形是解决问题的关键,并熟练掌握同高三角形面积的关系.
9.C
【分析】连接EM并延长交BC于点R,连接EN并延长交AB于点P,证明△BRM≌△HEM(AAS),推出RM=EM,BR=EH=2,同理可得△APN≌△FEN,推出PN=EN,AP=EF=2,勾股定理求出PR,根据三角形中位线的定义及性质求出MN.
【详解】解:如图,连接EM并延长交BC于点R,连接EN并延长交AB于点P,
∵正方形EFGH在正方形ABCD所在平面上平移,在平移过程中,始终保持EF∥AB,
∴BCEH,
∴∠RBM=∠EHM,∠BRM=∠HEM,
∵BM=MH,
∴△BRM≌△HEM(AAS),
∴RM=EM,BR=EH=2,
∵EFAB,
同理可得△APN≌△FEN,
∴PN=EN,AP=EF=2,
∴BP=AB-AP=6-2=4,
在Rt△BPR中,BP2+BR2=PR2,
∴42+22=PR2,
∴PR=2,
∵RM=EM,PN=EN,
∴MN是△PRE的中位线,
∴MN=PR=,
故选:C.
【点睛】此题考查了正方形及平移的性质,勾股定理,全等三角形的判定和性质,三角形中位线的定义和性质,正确理解题意并作出辅助线是解题的关键.
10.D
【分析】根据中位线的性质可求的长度,根据菱形的性质,勾股定理可求的长,由此即可求解.
【详解】解:∵点分别为边中点,
∴是的中位线,且,
∴,则,
∵四边形是菱形,
∴,,,
在中,,
∴菱形的周长为,
故选:.
【点睛】本题主要考查菱形的性质,中位线的性质,勾股定理的综合,掌握菱形的菱形,三角形中位线的性质,勾股定理求边长等知识的综合是解题的关键.
11.D
【分析】由勾股定理可求BD,由中位线,中线的性质求OE、EC,进而可求△COE的周长;
【详解】解:在矩形ABCD中,,
∴,
∵点O是BD的中点,
∴,
∵点E为AD的中点,
∴,,
∴,
∴△COE的周长为,
故选:D.
【点睛】本题主要考查勾股定理的应用、中位线的性质、中线的性质,掌握相关知识并灵活应用是解题的关键.
12.B
【分析】由菱形的性质先证明再求解 从而可得到答案.
【详解】解:菱形ABCD中,对角线相交于点O,E是的中点,
菱形ABCD的周长为
故选:B.
【点睛】本题考查的是菱形的性质,三角形的中位线的性质,掌握“三角形的中位线平行于第三边,并且等于第三边的一半”是解题的关键.
13./0.75
【分析】本题考查了三角形的中位线定理,平行四边形的判定与性质,掌握三角形的中位线定理是解题的关键.
由三角形的中位线定理得到,继而四边形均为平行四边形,则,即可求解.
【详解】解:∵D、E、F分别是的中点,
∴,
∴四边形均为平行四边形,
∴,
∴,
故答案为:.
14.10.5
【分析】将求GE+FH的最大值转化为GH-EF的值,因为EF是△ABC的中位线,EF=,AB的长度不变,所以只要GH的长最大即可,当GH为直径时,其长度最大.
【详解】如图,连接OA,OB,
∵∠ACB=30°,
∴∠AOB=60°.
∵OA=OB,
∴△OAB是等边三角形.
∴OA=OB=AB=7.
∵E、F是AC、BC的中点,
∴EF==3.5.
∵GE+FH=GH-EF,EF为定值,∴要使GE+FH最大,即要GH最大.
∴当GH为直径时,GE+FH的最大值为14-3.5=10.5.
【点睛】本题考查等边三角形的判定和三角形的中位线的性质.将求GE+FH的最大值转化为求GH-EF的最大值,是解题的关键.
15.2
【分析】连接BD,由矩形的性质可得AC=BD=4,由三角形的中位线定理可求解.
【详解】解:如图,连接BD,
∵四边形ABCD是矩形,
∴AC=BD=4,
∵E,F分别是AD,AB的中点,
∴EF=BD=2,
故答案为:2.
【点睛】本题考查了矩形的性质,三角形中位线定理,掌握矩形对角线相等是解题的关键.
16.4
【分析】本题主要考查了三角形中位线定理和菱形的判定方法,题目比较典型,又有综合性,难度较大.根据三角形的中位线定理和菱形的判定,可得顺次连接对角线相等的四边形各边中点所得四边形是菱形,根据菱形的性质得到,再由勾股定理得出的长,从而得到答案.
【详解】解:如图,设和相交于点O.
∵E、F、G、H分别是边,,,的中点,
∴分别是的中位线,分别是的中位线,
∴,
又∵,
∴,
∴四边形是菱形,
∴,
∴
,
∴.
故答案为:4.
17.3
【分析】根据三角形中位线定理和直角三角形的性质即可得到结论.
【详解】解:∵点D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∵BC=14,
∴DE=BC=7,
∵∠AFB=90°,AB=8,
∴DF=AB=4,
∴EF=DE-DF=7-4=3,
故答案为:3.
【点睛】本题考查了三角形中位线定理,直角三角形的性质,熟练掌握三角形中位线定理是解题的关键.
18.见解析
【分析】先取的三边的中点D、E、F,连接、、,即可得出答案.
【详解】解:如图,方法为:取的三边的中点D、E、F,连接、、,沿、、剪开,即可得出四个全等的三角形,
理由如下:
∵D,E,F分别为,,的中点,
∴,,,
∴,
∴,
同理可得:,
∴.
【点睛】本题考查了全等三角形的判定和三角形的中位线,能灵活运用定理进行推理是解此题的关键,通过此题培养了学生的思维能力和动手操作能力.
19.(1)见解析
(2)四边形AEBF是矩形,理由见解析
【分析】(1)由等腰三角形的性质可得CE=BE,∠AEB=90°,由三角形的中位线定理可得EO∥AC,由直角三角形的性质和平行线的性质可证OE=OF;
(2)由矩形的判定可得结论.
【详解】(1)证明:∵AB=AC,AE是∠BAC的角平分线,
∴CE=BE,∠AEB=90°,
∵点O是AB的中点,
∴EO是△ABC的中位线,EO=AO=BO,
∴EO∥AC,
∴∠EFA=∠FAD,
∵AF平分∠BAD,
∴∠FAD=∠FAB,
∴∠FAB=∠EFA,
∴OF=AO,
∴OE=OF;
(2)解:四边形AEBF是矩形,理由如下:
如图,
∵AO=BO,EO=FO,
∴四边形AEBF是平行四边形,
∵∠AEB=90°,
∴四边形AEBF是矩形.
【点睛】本题考查了矩形的判定,等腰三角形的性质,三角形中位线定理等知识,灵活运用这些性质解决问题是解题的关键.
20.(1)证明见解析;(2)结论仍然成立;(3)
【分析】(1)利用等边三角形的性质以及三线合一证明得出结论;
(2)由中位线的性质、平行线的性质,等边三角形的性质以及三角形全等的判定与性质证明
【详解】(1)证明:∵ΔABC是等边三角形,
∴∠ABC=∠ACB=,AB=BC=AC
∵DE是中位线,
∴E是AC的中点,
∴BE平分∠ABC,AE=EC
∴∠EBC=∠ABC=
∵AE=CF,
∴CE=CF,
∴∠CEF=∠F
∵∠CEF+∠F=∠ACB=,
∴∠F=,
∴∠EBC=∠F,
∴BE=EF
(2)结论仍然成立.
∵DE是由中位线平移所得;
∴DE//BC,
∴∠ADE=∠ABC=,∠AED=∠ACB=,
∴ΔADE是等边三角形,
∴DE=AD=AE,
∵AB=AC,
∴BD=CE,
∵AE=CF,
∴DE=CF
∵∠BDE=-∠ADE=,∠FCE=-∠ACB=,
∴∠FCE=∠EDB,
∴ΔBDE≌ΔECF,
∴BE=EF
【点睛】此题考查等边三角形的判定与性质,三角形中位线定理和全等三角形的判定与性质,解题关键在于利用三线合一证明得出结论
21.(1)见解析;
(2).
【分析】(1)利用平行线的性质,可得,即可求证;
(2)根据三角形中位线的性质,可得,由(1)可得,则
【详解】(1)证明:∵,
∴,
∵为的中点,
∴,
又∵,
∴;
(2)解:∵为的中点,点B为线段的中点,
∴为的中位线,,
∴,
由(1)得,
∴,即,
∴.
【点睛】此题考查了全等三角形的判定与性质,三角形中位线的性质,平行线的性质,解题的关键是熟练掌握相关基础性质.
22.(1)证明见解析
(2),理由见解析
【分析】(1)首先利用三角形中位线的性质得出,,,,从而得出,,即可证得四边形是平行四边形;
(2)由四边形是菱形,可得,再根据三角形中位线的性质可得,,从而得出.
【详解】(1)证明:∵D、E分别是边、的中点.
∴,,
∵点G、F分别是、的中点,
∴,,
∴四边形是平行四边形;
(2)解:,理由如下:
连接,
∵四边形是菱形,
∴,
∵D是的中点,点G、F分别是、的中点,
∴,,
∴.
【点睛】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,菱形的判定以及平行四边形与菱形的关系,熟记相关的定理和性质是解题的关键.
23.(1)见解析
(2)2
(3)
【分析】本题考查菱形的性质,平行四边形的判定和性质,中位线的性质等综合题型,解题的关键对菱形性质和图形变化极值情况的熟练掌握.
(1)根据平行四边形判定及性质进行证明即可;
(2)如图,连接,由菱形知,可证,四边形是平行四边形,于是,由勾股定理中,,所以菱形的面积即可求得;
(3)如图,点在延长线上(可以与点重合),得;随着的减小,点逐渐向点接近,当点与点重合时,最小,由矩形性质得,进一步证得,由三角形内角和定理,得,于是.
【详解】(1)证明:∵是的中位线,
∴是中点,
又,
∴四边形是平行四边形,
∴,
∵,
∴,且,
∴四边形是平行四边形,即四边形是平行四边形;
(2)解:如图2,连接,
∵四边形是菱形,
∴,
∴,
∵,
∴,
∵,
∴四边形是平行四边形,
∴,
在中,,
∴,
∵,
∴,
∴,
∴菱形的面积为2;
(3)解:如图,点在延长线上(可以与点重合),
∴,
随着的减小,点逐渐向点接近,当点与点重合时,最小,如图,四边形是矩形,
,
而,
,
,
,
.
24.见解析
【分析】由DE、DF是△ABC的中位线,得出DE∥AB,DF∥AC,进而证明四边形AEDF是平行四边形,再根据条件∠BAC=90°,证得平行四边形AEDF是矩形即可得出结论.
【详解】证明:∵DE,DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
又∵∠BAC=90°,
∴平行四边形AEDF是矩形,
∴EF=AD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
