2024-2025学年北师大版九年级数学下册 3.6 课时2 切线的判定及内切圆 课件 (共29张PPT)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学下册 3.6 课时2 切线的判定及内切圆 课件 (共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 810.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 08:12:20 | ||
图片预览








文档简介
(共29张PPT)
第三章 圆
3.6 直线和圆的位置关系
课时2 切线的判定及内切圆
1.圆的切线的判定;
2.三角形的内切圆. (重点、难点)
学习目标
新课导入
1.直线和圆有哪些位置关系?
相交、相切、相离
2.切线的性质是什么?
性质:圆的切线垂直于过切点的半径.
几何语言:如图所示,
∵直线l切☉O于T,∴OT⊥l.
新课讲解
如图,在⊙O中,经过半径 OA 的外端点 A 作直线
l⊥OA,则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O
有什么位置关系?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
l
O
A
新课讲解
例
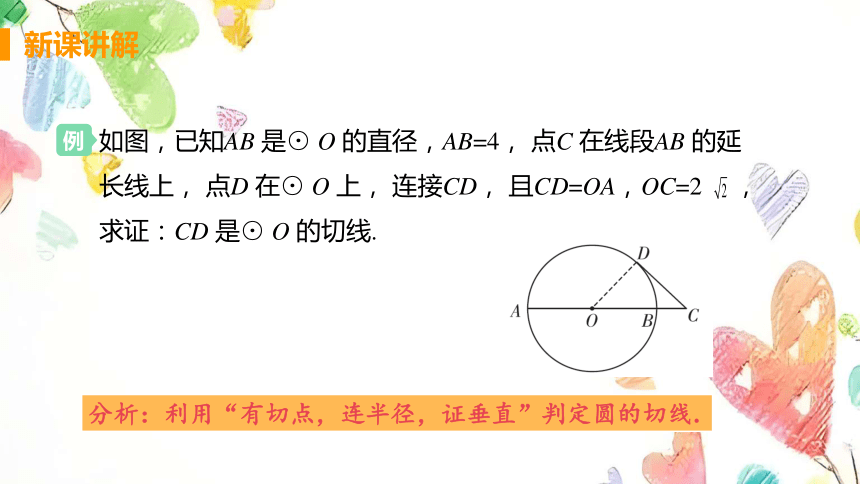
如图,已知AB 是⊙ O 的直径,AB=4, 点C 在线段AB 的延长线上, 点D 在⊙ O 上, 连接CD, 且CD=OA,OC=2 ,求证:CD 是⊙ O 的切线.
分析:利用“有切点,连半径,证垂直”判定圆的切线.
新课讲解
证明:连接OD.
由题意可知CD=OD=OA= AB=2.
∵ OC=2 ,∴ OD2+CD2=OC2.
∴∠ ODC=90°,即OD ⊥ CD.
又点D 在⊙ O 上,∴ CD 是⊙ O 的切线.
新课讲解
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的
切线.
新课讲解
已知:△ABC(如图).
求作: ⊙ I,使它与△ ABC的三边都相切.
新课讲解
作法:
1.作∠B , ∠C的平分线BE和CF,交点为I,如图.
2.过I作BC的垂线,垂足为D.
3.以I为圆心,以ID为半径作⊙I.
⊙I就是所求的圆.
新课讲解
定义:和三角形三边都相切的圆叫做三角形的内切
圆.内切圆的圆心是三角形三条角平分线的交点,
叫做三角形的内心.
新课讲解
图形 ⊙O的名称 △ABC的名称 圆心O的确定 “心”的性质 “心”的位置
△ABC的内切圆 ⊙O的外切三角形 三角形三条角平分线的交点 到三角形的三条边的距离相等 一定在三角形内部
课堂小结
切线的三种判定方法:
(1)定义;
(2)数量关系;
(3)位置关系(切线的判定定理):经过半径外端并且
垂直于这条半径的直线是圆的切线.
在切线的三种判定方法中,常用的是后两种判定
方法,在判定圆的切线时,往往需要添加辅助线.
当堂小练
1.如图,AB是⊙O的直径,线段BC与⊙O的交点D是BC的中点,DE⊥AC于点E,连接AD,则下列结论中正确的个数是( )
①AD⊥BC;②∠EDA=∠B;
③OA= AC;④DE是⊙O的切线.
A.1 B.2
C.3 D.4
D
当堂小练
2.如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )
A.△ACD的外心
B.△ABC的外心
C.△ACD的内心
D.△ABC的内心
B
拓展与延伸
如图,点O为∠MPN的平分线上一点,以点O为圆心的⊙O与PN相切于点A. 求证:PM为⊙O的切线.
拓展与延伸
如图,连接OA,过点O作OB⊥PM于点B.
∵PN与⊙O相切于点A,
∴OA⊥PN.
∵点O在∠MPN的平分线上,
OB⊥PM,
∴OB=OA.
∴点O到直线PM的距离等于⊙O的半径.
∴PM为⊙O的切线.
证明:
1.(北师9下P93、人教9上P101)如图,直线AB经过☉O上的点C,并且OA=OB,CA=CB.求证:AB是☉O的切线.
证明:如图,连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB,
∵点C在☉O上,
∴AB是☉O的切线.
答案图
课后练习
2.(北师9下P93、人教9上P100改编)如图,在△ABC中,点P是△ABC的内心,∠A=68°,则∠BPC的度数为
.
124°
3.(北师9下P105、人教9上P99)已知△ABC,用尺规作△ABC的内切圆☉O.
图略(提示:作∠B和∠C的平分线,它们相交于点O,过点O作OD⊥BC于D,然后以点O为圆心,OD长为半径作☉O即可)
4.(人教9上P102改编)(2024西藏)如图,AB为☉O的直径,C,D是☉O上两点,BD平分∠ABC,BC的延长线与过点D的直线交于点H,且BH⊥DH.求证:DH是☉O的切线.
证明:连接半径OD.
∵BD平分∠ABH,∴∠ABD=∠HBD,
∵OD=OB,∴∠ODB=∠OBD,
∴∠HBD=∠ODB,∴OD∥BH,
又∵BH⊥DH,∴OD⊥DH,
∵点D在☉O上,∴DH是☉O的切线.
小结:通过平行证垂直
5.(北师9下P95、人教9上P103)如图,☉O是Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AC=6 cm,BC=8 cm,则☉O的半径是 .
2 cm
6.如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作☉O交BC于点D,点E在边AC上,且满足ED=EA.
(1)求∠DOA的度数;
(2)求证:ED是☉O的切线.
(1)解:∵OD=OB,∴∠DBA=∠ODB.
∵∠DBA=50°,∴∠DOA=2∠DBA=100°.
(2)证明:如图,连接OE.
在△EAO与△EDO中,,
∴△EAO≌△EDO(SSS),∴∠EDO=∠EAO,
∵∠BAC=90°,∴∠EDO=90°,
又点D在☉O上,∴ED是☉O的切线.
(2)求证:ED是☉O的切线.
小结:通过全等或等量代换证垂直
7.如图,线段AB经过圆心O,交☉O于点A,C,∠BAD=∠B=30°,边BD交☉O于点D,连接OD.BD是☉O的切线吗?为什么?
解:BD是☉O的切线,理由如下:
∵∠BAD=∠B=30°,
∴∠ADB=180°-30°-30°=120°,
∵AO=DO,∴∠A=∠ADO=30°,
∴∠ODB=120°-30°=90°,即OD⊥BD.
∵点D在☉O上,∴BD是☉O的切线.
小结:通过直接计算证垂直
8.(北师9下P107、人教9上P100)如图,已知△ABC的内切圆☉O的半径为r,△ABC的周长为l,则△ABC的面积S=
___________.
lr
★9. 0.50 如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的☉O与BC相切于点M,与AB,AD分别相交于点E,F.
(1)求证:CD与☉O相切;
(2)若☉O的半径为,求正方形ABCD的边长.
(1)证明:如图,连接OM,过点O作ON⊥CD,垂足为N,
∵☉O与BC相切于点M,∴OM⊥BC.
∵四边形ABCD是正方形,∴AC平分∠BCD,
又∵ON⊥CD,OM⊥BC,∴OM=ON.
∵ON⊥CD,∴CD与☉O相切.
(2)若☉O的半径为,求正方形ABCD的边长.
(2)解:设正方形ABCD的边长为a,∴AC=a.
∵∠OCM=∠ACB,∠OMC=∠B=90°,
∴△COM∽△CAB,,
,解得a=+1.
∴正方形ABCD的边长为+1.
小结:公共点未知问题,作垂线,得d=r,证垂直.
请完成课本本节对应习题
布置作业
谢谢大家
第三章 圆
3.6 直线和圆的位置关系
课时2 切线的判定及内切圆
1.圆的切线的判定;
2.三角形的内切圆. (重点、难点)
学习目标
新课导入
1.直线和圆有哪些位置关系?
相交、相切、相离
2.切线的性质是什么?
性质:圆的切线垂直于过切点的半径.
几何语言:如图所示,
∵直线l切☉O于T,∴OT⊥l.
新课讲解
如图,在⊙O中,经过半径 OA 的外端点 A 作直线
l⊥OA,则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O
有什么位置关系?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
l
O
A
新课讲解
例
如图,已知AB 是⊙ O 的直径,AB=4, 点C 在线段AB 的延长线上, 点D 在⊙ O 上, 连接CD, 且CD=OA,OC=2 ,求证:CD 是⊙ O 的切线.
分析:利用“有切点,连半径,证垂直”判定圆的切线.
新课讲解
证明:连接OD.
由题意可知CD=OD=OA= AB=2.
∵ OC=2 ,∴ OD2+CD2=OC2.
∴∠ ODC=90°,即OD ⊥ CD.
又点D 在⊙ O 上,∴ CD 是⊙ O 的切线.
新课讲解
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的
切线.
新课讲解
已知:△ABC(如图).
求作: ⊙ I,使它与△ ABC的三边都相切.
新课讲解
作法:
1.作∠B , ∠C的平分线BE和CF,交点为I,如图.
2.过I作BC的垂线,垂足为D.
3.以I为圆心,以ID为半径作⊙I.
⊙I就是所求的圆.
新课讲解
定义:和三角形三边都相切的圆叫做三角形的内切
圆.内切圆的圆心是三角形三条角平分线的交点,
叫做三角形的内心.
新课讲解
图形 ⊙O的名称 △ABC的名称 圆心O的确定 “心”的性质 “心”的位置
△ABC的内切圆 ⊙O的外切三角形 三角形三条角平分线的交点 到三角形的三条边的距离相等 一定在三角形内部
课堂小结
切线的三种判定方法:
(1)定义;
(2)数量关系;
(3)位置关系(切线的判定定理):经过半径外端并且
垂直于这条半径的直线是圆的切线.
在切线的三种判定方法中,常用的是后两种判定
方法,在判定圆的切线时,往往需要添加辅助线.
当堂小练
1.如图,AB是⊙O的直径,线段BC与⊙O的交点D是BC的中点,DE⊥AC于点E,连接AD,则下列结论中正确的个数是( )
①AD⊥BC;②∠EDA=∠B;
③OA= AC;④DE是⊙O的切线.
A.1 B.2
C.3 D.4
D
当堂小练
2.如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )
A.△ACD的外心
B.△ABC的外心
C.△ACD的内心
D.△ABC的内心
B
拓展与延伸
如图,点O为∠MPN的平分线上一点,以点O为圆心的⊙O与PN相切于点A. 求证:PM为⊙O的切线.
拓展与延伸
如图,连接OA,过点O作OB⊥PM于点B.
∵PN与⊙O相切于点A,
∴OA⊥PN.
∵点O在∠MPN的平分线上,
OB⊥PM,
∴OB=OA.
∴点O到直线PM的距离等于⊙O的半径.
∴PM为⊙O的切线.
证明:
1.(北师9下P93、人教9上P101)如图,直线AB经过☉O上的点C,并且OA=OB,CA=CB.求证:AB是☉O的切线.
证明:如图,连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB,
∵点C在☉O上,
∴AB是☉O的切线.
答案图
课后练习
2.(北师9下P93、人教9上P100改编)如图,在△ABC中,点P是△ABC的内心,∠A=68°,则∠BPC的度数为
.
124°
3.(北师9下P105、人教9上P99)已知△ABC,用尺规作△ABC的内切圆☉O.
图略(提示:作∠B和∠C的平分线,它们相交于点O,过点O作OD⊥BC于D,然后以点O为圆心,OD长为半径作☉O即可)
4.(人教9上P102改编)(2024西藏)如图,AB为☉O的直径,C,D是☉O上两点,BD平分∠ABC,BC的延长线与过点D的直线交于点H,且BH⊥DH.求证:DH是☉O的切线.
证明:连接半径OD.
∵BD平分∠ABH,∴∠ABD=∠HBD,
∵OD=OB,∴∠ODB=∠OBD,
∴∠HBD=∠ODB,∴OD∥BH,
又∵BH⊥DH,∴OD⊥DH,
∵点D在☉O上,∴DH是☉O的切线.
小结:通过平行证垂直
5.(北师9下P95、人教9上P103)如图,☉O是Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AC=6 cm,BC=8 cm,则☉O的半径是 .
2 cm
6.如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作☉O交BC于点D,点E在边AC上,且满足ED=EA.
(1)求∠DOA的度数;
(2)求证:ED是☉O的切线.
(1)解:∵OD=OB,∴∠DBA=∠ODB.
∵∠DBA=50°,∴∠DOA=2∠DBA=100°.
(2)证明:如图,连接OE.
在△EAO与△EDO中,,
∴△EAO≌△EDO(SSS),∴∠EDO=∠EAO,
∵∠BAC=90°,∴∠EDO=90°,
又点D在☉O上,∴ED是☉O的切线.
(2)求证:ED是☉O的切线.
小结:通过全等或等量代换证垂直
7.如图,线段AB经过圆心O,交☉O于点A,C,∠BAD=∠B=30°,边BD交☉O于点D,连接OD.BD是☉O的切线吗?为什么?
解:BD是☉O的切线,理由如下:
∵∠BAD=∠B=30°,
∴∠ADB=180°-30°-30°=120°,
∵AO=DO,∴∠A=∠ADO=30°,
∴∠ODB=120°-30°=90°,即OD⊥BD.
∵点D在☉O上,∴BD是☉O的切线.
小结:通过直接计算证垂直
8.(北师9下P107、人教9上P100)如图,已知△ABC的内切圆☉O的半径为r,△ABC的周长为l,则△ABC的面积S=
___________.
lr
★9. 0.50 如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的☉O与BC相切于点M,与AB,AD分别相交于点E,F.
(1)求证:CD与☉O相切;
(2)若☉O的半径为,求正方形ABCD的边长.
(1)证明:如图,连接OM,过点O作ON⊥CD,垂足为N,
∵☉O与BC相切于点M,∴OM⊥BC.
∵四边形ABCD是正方形,∴AC平分∠BCD,
又∵ON⊥CD,OM⊥BC,∴OM=ON.
∵ON⊥CD,∴CD与☉O相切.
(2)若☉O的半径为,求正方形ABCD的边长.
(2)解:设正方形ABCD的边长为a,∴AC=a.
∵∠OCM=∠ACB,∠OMC=∠B=90°,
∴△COM∽△CAB,,
,解得a=+1.
∴正方形ABCD的边长为+1.
小结:公共点未知问题,作垂线,得d=r,证垂直.
请完成课本本节对应习题
布置作业
谢谢大家
