华师大版七年级数学下册第八章一元一次不等式第3节一元一次不等式组
文档属性
| 名称 | 华师大版七年级数学下册第八章一元一次不等式第3节一元一次不等式组 | 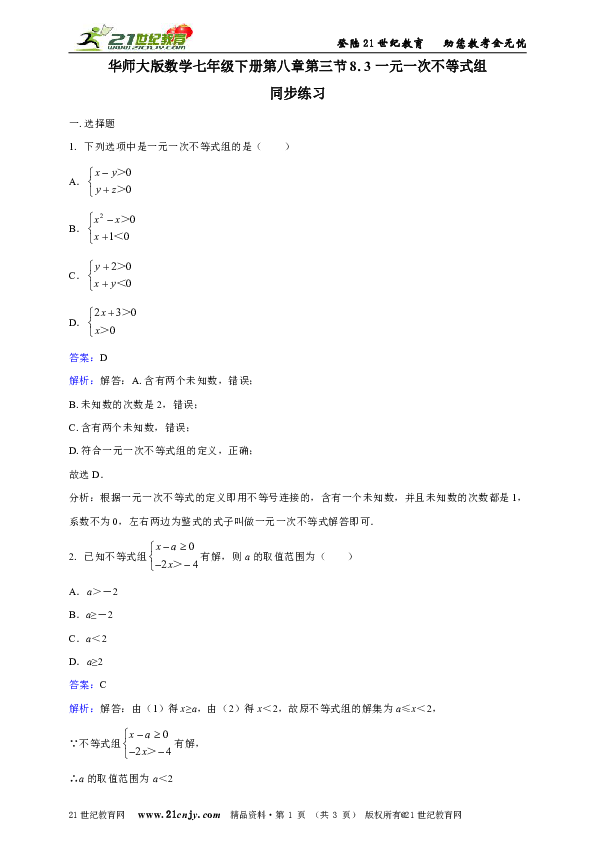 | |
| 格式 | doc | ||
| 文件大小 | 160.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-21 11:21:14 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学七年级下册第八章第三节8.3一元一次不等式组
同步练习
一.选择题
1. 下列选项中是一元一次不等式组的是( )
A.
B.
C.
D.
答案:D
解析:解答:A.含有两个未知数,错误;
B.未知数的次数是2,错误;
C.含有两个未知数,错误;
D.符合一元一次不等式组的定义,正确;
故选D.
分析:根据一元一次不等式的定义即用不等号连接的,含有一个未知数,并且未知数的次数都是1,系数不为0,左右两边为整式的式子叫做一元一次不等式解答即可.
2. 已知不等式组有解,则a的取值范围为( )
A.a>-2
B.a≥-2
C.a<2
D.a≥2
答案:C
解析:解答:由(1)得x≥a,由(2)得x<2,故原不等式组的解集为a≤x<2,
∵不等式组有解,
∴a的取值范围为a<2
分析:分别解这两个不等式,得出解集,既然有解,根据同大取较大,同小取较小,小大大小中间找,大大小小解不了的原则,建立适当的不等式,进行解答.
3. 下列不等式组中,是一元一次不等式组的是( )
A.
B.
C.
D.
答案:C
解析:解答:A.含有2个未知数,不是一元一次不等式组,故本选项错误;
B.含有分式,不是一元一次不等式组,故本选项错误;
C.符合一元一次不等式组的定义,故本选项正确;
D.最高次数是2,不是一元一次不等式组,故本选项错误.
故选C.
分析:根据一元一次不等式组的定义判定则可.由几个含有相同未知数的一元一次不等式所组成的一组不等式叫做一元一次不等式组.
4. 不等式组的解集是( )
A.-1<x<2
B.1<x≤2
C.-1<x≤2
D.-1<x≤3
答案:C
解析:解答:,
∵由①得,x≤2;
由②得,x>-1,
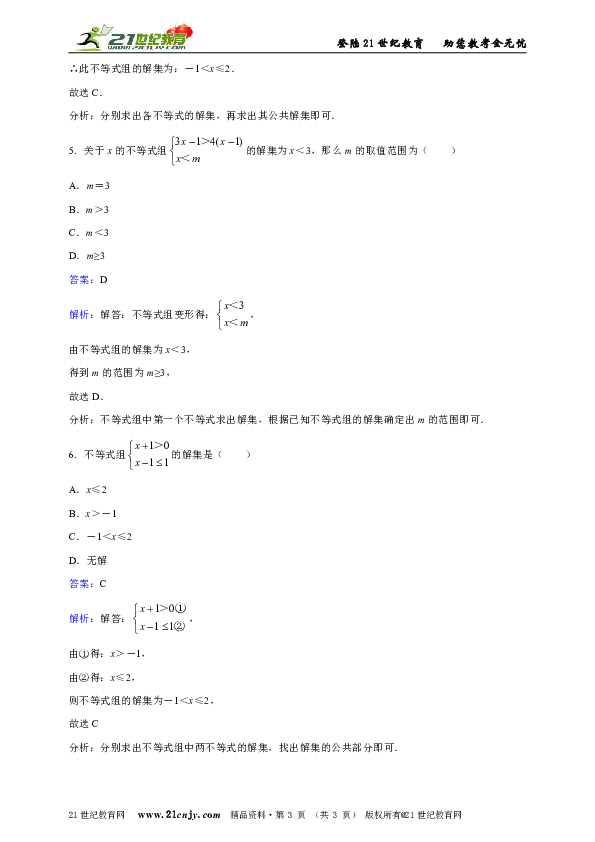
∴此不等式组的解集为:-1<x≤2.
故选C.
分析:分别求出各不等式的解集,再求出其公共解集即可.
5. 关于x的不等式组的解集为x<3,那么m的取值范围为( )
A.m=3
B.m>3
C.m<3
D.m≥3
答案:D
解析:解答:不等式组变形得:,
由不等式组的解集为x<3,
得到m的范围为m≥3,
故选D.
分析:不等式组中第一个不等式求出解集,根据已知不等式组的解集确定出m的范围即可.
6. 不等式组的解集是( )
A.x≤2
B.x>-1
C.-1<x≤2
D.无解
答案:C
解析:解答:,
由①得:x>-1,
由②得:x≤2,
则不等式组的解集为-1<x≤2,
故选C
分析:分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
7. 不等式组的解集是( )
A.x>1
B.x<2
C.1≤x≤2
D.1<x<2
答案:D
解析:解答:
∵解不等式①得:x<2,
解不等式②得:x>1,
∴不等式组的解集为1<x<2,
故选D.分析:先求出每个不等式的解集,再根据找不等式组解集的规律找出即可.
8. 不等式组 的解集是( )
A.1<x≤2
B.-1<x≤2
C.x>-1
D.-1<x≤4
答案:B
解析:解答: ,
解①得x>-1,
解②得x≤2,
所以不等式组的解集为-1<x≤2.
故选B.
分析:分别解两个不等式得到x>-1和x≤2,然后根据大小小大中间找确定不等数组的解集.
9. 使不等式x-1≥2与3x-7<8同时成立的x的整数值是( )
A.3,4
B.4,5
C.3,4,5
D.不存在
答案:A
解析:解答:根据题意得:
,
解得:3≤x<5,
则x的整数值是3,4;
故选A.
分析:先分别解出两个一元一次不等式,再确定x的取值范围,最后根据x的取值范围找出x的整数解即可.
10. 一元一次不等式组的解集中,整数解的个数是( )
A.4
B.5
C.6
D.7
答案:C
解析:解答:
∵解不等式①得:x>-0.5,
解不等式②得:x≤5,
∴不等式组的解集为-0.5<x≤5,
∴不等式组的整数解为0,1,2,3,4,5,共6个,
故选C.
分析:先求出每个不等式的解集,再求出不等式组的解集,求出不等式组的整数解,即可得出答案.
11. 不等式组的所有整数解的和是( )
A.2
B.3
C.5
D.6
答案:D
解析:解答:
∵解不等式①得; ,
解不等式②得;x≤3,
∴不等式组的解集为,
∴不等式组的整数解为0,1,2,3,
0+1+2+3=6,
故选D.
分析:先求出不等式组的解集,再求出不等式组的整数解,最后求出答案即可.
12. 定义[x]为不超过x的最大整数,如[3.6]=3,[0.6]=0,[-3.6]=-4.对于任意实数x,下列式子中错误的是( )
A.[x]=x(x为整数)
B.0≤x-[x]<1
C.[x+y]≤[x]+[y]
D.[n+x]=n+[x](n为整数)
答案:C
解析:解答:A.∵[x]为不超过x的最大整数,
∴当x是整数时,[x]=x,成立;
B.∵[x]为不超过x的最大整数,
∴0≤x-[x]<1,成立;
C.例如,[-5.4-3.2]=[-8.6]=-9,[-5.4]+[-3.2]=-6+(-4)=-10,
∵-9>-10,
∴[-5.4-3.2]>[-5.4]+[-3.2],
∴[x+y]≤[x]+[y]不成立,
D.[n+x]=n+[x](n为整数),成立;
故选:C.
分析:根据“定义[x]为不超过x的最大整数”进行计算.
13. 我们规定:对于有理数x,符号[x]表示不大于x的最大整数,例如:[4.7]=4,[3]=3,[-π]=-4,如果[x]=-3,那么x的取值范围是( )
A.-3≤x<-2
B.-3<x≤-2
C.-3<x<-2
D.-3≤x≤-2
答案:A
解析:解答:∵对于有理数x,符号[x]表示不大于x的最大整数,[x]=-3,
∴,
解得:-3≤x<-2.
故选:A.
分析:根据最大整数的定义即可求解.
14. 宁城县城区现行出租车的收费标准:起步价5元(即行驶距离不超过3千米都需付5元车费),超过3千米后,每增加1千米,加收1.5元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共付车费11元,那么甲地到乙地路程的最大值是( )
A.5千米
B.7千米
C.8千米
D.9千米
答案:B
解析:解答:依题意得:1.5(x-3)≤11-5,
x-3≤4,
x≤7.
因此甲地到乙地路程的最大值是7千米.
故选:B.
分析:本题可先用11减去5得到6,则1.5(x-3)≤6,解出x的值,取最大整数即为本题的解.
15. 已知非负数a,b,c满足条件a+b=7,c-a=5,设S=a+b+c的最大值为m,最小值为n,则m-n的值( )
A.5
B.6
C.7
D.8
答案:C
解析:解答:∵a,b,c为非负数;
∴S=a+b+c≥0;
又∵c-a=5;
∴c=a+5;
∴c≥5;
∵a+b=7;
∴S=a+b+c=7+c;
又∵c≥5;
∴c=5时S最小,即S最小=12,即n=12;
∵a+b=7;
∴a≤7;
∴S=a+b+c=7+c=7+a+5=12+a;
∴a=7时S最大,即S最大=19,即m=19;
∴m-n=19-12=7.
故选C.
分析:由于已知a,b,c为非负数,所以m.n一定≥0;根据a+b=7和c-a=5推出c的最小值与a的最大值;然后再根据a+b=7和c-a=5把S=a+b+c转化为只含a或c的代数式,从而确定其最大值与最小值.
二.填空题
16. 写出一个无解的一元一次不等式组为________.
答案:
解析:解答:根据不等式组解集的口诀:大大小小找不到(无解),
可写x≤2,x≥3,
即.
分析:由题意写出一个无解的一元一次不等式组主要考查,其简便求法就是用口诀求解,根据不等式组解集的口诀:大大小小找不到(无解),来写出一个无解的一元一次不等式组.
17. 试构造一个解为x<-1的一元一次不等式组________.
答案:
解析:解答: .
答案不唯一
分析:本题为开放性题,根据同小取小列不等式组即可.
18. 不等式组 的所有整数解是________.
答案:0,1
解析:解答:,
解不等式①得,,
解不等式②得,x≤1,
所以不等式组的解集为,
所以原不等式组的整数解是0,1.
故答案为:0,1.
分析:先求出两个不等式的解集,再求其公共解,然后写出范围内的整数即可.
19. 对于任意实数m.n,定义一种运运算m※n=mn-m-n+3,等式的右边是通常的加减和乘法运算,例如:3※5=3×5-3-5+3=10.请根据上述定义解决问题:若a<2※x<7,且解集中有两个整数解,则a的取值范围是________.
答案:4≤a<5
解析:解答:根据题意得:2※x=2x-2-x+3=x+1,
∵a<x+1<7,即a-1<x<6解集中有两个整数解,
∴a的范围为4≤a<5,
故答案为:4≤a<5.
分析:利用题中的新定义化简所求不等式,求出a的范围即可.
20. 将不足40只鸡放入若干个笼中,若每个笼里放4只,则有一只鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,且最后一笼不足3只.则有鸡________只.
答案:37
解析:解答:设笼有x个.
,
解得:8<x<11
x=9时,4×9+1=37
x=10时,4×10+1=41(舍去).
故笼有9个,鸡有37只.
故答案是:37.
分析:设笼有x个,那么鸡就有(4x+1)只,根据若每个笼里放5只,则有一笼无鸡可放,且最后一笼不足3只,可列出不等式求解.
三.解答题
21. 解不等式组:,并求它的整数解的和.
答案:解答:由①得x>-2
由②得x≤1
∴不等式组的解集为-2<x≤1
∴不等式组的整数解的和为-1+0+1=0.
解析:分析:先求出不等式组中每个不等式的解集,然后求出其公共解集,进而求其整数解,最后求它的整数解的和即可.
22. 求不等式组的整数解.
答案:解答:
解不等式①,得 x>-2,
解不等式②,得 x<1.
不等式组的解集为-2<x<1,
所以原不等式组的整数解为-1,0.
解析:分析:首先求出不等式组中每一个不等式的解集,再根据大小小大中间找确定不等式组的解集即可.
23. 若不等式的整数解有5个,则m的取值范围是多少?
答案:解答:,
由①得:x>3,
由②得:x<m+1,
∴3<x<m+1,
∵不等式组有5个整数解,即:4.5.6.7.8,
∴8<m+1≤9,
∴7<m≤8,
答案为7<m≤8.
解析:分析:认真审题,首先用含有m的代数式表示出x的取值范围,再根据整数解的个数,即可求出本题的答案.
24. 解不等式组,并求它的整数解.
答案:解答:由①得:2x+4≤5x+10,
∴-3x≤6,
∴x≥-2.
由②得:,
∴x<3.
所以原不等式组的解集为-2≤x<3.
所以原不等式组的整数解为-2,-1,0,1,2.
解析:分析:分别得出不等式的解集,进而得出不等式组的解集,即可得出不等式组的整数解.
25. 一个矩形,两边长分别为x和15,如果它的周长小于60,面积大于195,求x的值.(长和宽都为正整数)
答案:解答:根据题意得:,
解得:13<x<15,
由x为正整数,得到x=14,
则x的值为14.
解析:分析:根据周长小于60,面积大于195列出不等式组,求出不等式组的解集,找出解集中的正整数解即可确定出x的值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 11 页 (共 12 页) 版权所有@21世纪教育网
华师大版数学七年级下册第八章第三节8.3一元一次不等式组
同步练习
一.选择题
1. 下列选项中是一元一次不等式组的是( )
A.
B.
C.
D.
答案:D
解析:解答:A.含有两个未知数,错误;
B.未知数的次数是2,错误;
C.含有两个未知数,错误;
D.符合一元一次不等式组的定义,正确;
故选D.
分析:根据一元一次不等式的定义即用不等号连接的,含有一个未知数,并且未知数的次数都是1,系数不为0,左右两边为整式的式子叫做一元一次不等式解答即可.
2. 已知不等式组有解,则a的取值范围为( )
A.a>-2
B.a≥-2
C.a<2
D.a≥2
答案:C
解析:解答:由(1)得x≥a,由(2)得x<2,故原不等式组的解集为a≤x<2,
∵不等式组有解,
∴a的取值范围为a<2
分析:分别解这两个不等式,得出解集,既然有解,根据同大取较大,同小取较小,小大大小中间找,大大小小解不了的原则,建立适当的不等式,进行解答.
3. 下列不等式组中,是一元一次不等式组的是( )
A.
B.
C.
D.
答案:C
解析:解答:A.含有2个未知数,不是一元一次不等式组,故本选项错误;
B.含有分式,不是一元一次不等式组,故本选项错误;
C.符合一元一次不等式组的定义,故本选项正确;
D.最高次数是2,不是一元一次不等式组,故本选项错误.
故选C.
分析:根据一元一次不等式组的定义判定则可.由几个含有相同未知数的一元一次不等式所组成的一组不等式叫做一元一次不等式组.
4. 不等式组的解集是( )
A.-1<x<2
B.1<x≤2
C.-1<x≤2
D.-1<x≤3
答案:C
解析:解答:,
∵由①得,x≤2;
由②得,x>-1,
∴此不等式组的解集为:-1<x≤2.
故选C.
分析:分别求出各不等式的解集,再求出其公共解集即可.
5. 关于x的不等式组的解集为x<3,那么m的取值范围为( )
A.m=3
B.m>3
C.m<3
D.m≥3
答案:D
解析:解答:不等式组变形得:,
由不等式组的解集为x<3,
得到m的范围为m≥3,
故选D.
分析:不等式组中第一个不等式求出解集,根据已知不等式组的解集确定出m的范围即可.
6. 不等式组的解集是( )
A.x≤2
B.x>-1
C.-1<x≤2
D.无解
答案:C
解析:解答:,
由①得:x>-1,
由②得:x≤2,
则不等式组的解集为-1<x≤2,
故选C
分析:分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
7. 不等式组的解集是( )
A.x>1
B.x<2
C.1≤x≤2
D.1<x<2
答案:D
解析:解答:
∵解不等式①得:x<2,
解不等式②得:x>1,
∴不等式组的解集为1<x<2,
故选D.分析:先求出每个不等式的解集,再根据找不等式组解集的规律找出即可.
8. 不等式组 的解集是( )
A.1<x≤2
B.-1<x≤2
C.x>-1
D.-1<x≤4
答案:B
解析:解答: ,
解①得x>-1,
解②得x≤2,
所以不等式组的解集为-1<x≤2.
故选B.
分析:分别解两个不等式得到x>-1和x≤2,然后根据大小小大中间找确定不等数组的解集.
9. 使不等式x-1≥2与3x-7<8同时成立的x的整数值是( )
A.3,4
B.4,5
C.3,4,5
D.不存在
答案:A
解析:解答:根据题意得:
,
解得:3≤x<5,
则x的整数值是3,4;
故选A.
分析:先分别解出两个一元一次不等式,再确定x的取值范围,最后根据x的取值范围找出x的整数解即可.
10. 一元一次不等式组的解集中,整数解的个数是( )
A.4
B.5
C.6
D.7
答案:C
解析:解答:
∵解不等式①得:x>-0.5,
解不等式②得:x≤5,
∴不等式组的解集为-0.5<x≤5,
∴不等式组的整数解为0,1,2,3,4,5,共6个,
故选C.
分析:先求出每个不等式的解集,再求出不等式组的解集,求出不等式组的整数解,即可得出答案.
11. 不等式组的所有整数解的和是( )
A.2
B.3
C.5
D.6
答案:D
解析:解答:
∵解不等式①得; ,
解不等式②得;x≤3,
∴不等式组的解集为,
∴不等式组的整数解为0,1,2,3,
0+1+2+3=6,
故选D.
分析:先求出不等式组的解集,再求出不等式组的整数解,最后求出答案即可.
12. 定义[x]为不超过x的最大整数,如[3.6]=3,[0.6]=0,[-3.6]=-4.对于任意实数x,下列式子中错误的是( )
A.[x]=x(x为整数)
B.0≤x-[x]<1
C.[x+y]≤[x]+[y]
D.[n+x]=n+[x](n为整数)
答案:C
解析:解答:A.∵[x]为不超过x的最大整数,
∴当x是整数时,[x]=x,成立;
B.∵[x]为不超过x的最大整数,
∴0≤x-[x]<1,成立;
C.例如,[-5.4-3.2]=[-8.6]=-9,[-5.4]+[-3.2]=-6+(-4)=-10,
∵-9>-10,
∴[-5.4-3.2]>[-5.4]+[-3.2],
∴[x+y]≤[x]+[y]不成立,
D.[n+x]=n+[x](n为整数),成立;
故选:C.
分析:根据“定义[x]为不超过x的最大整数”进行计算.
13. 我们规定:对于有理数x,符号[x]表示不大于x的最大整数,例如:[4.7]=4,[3]=3,[-π]=-4,如果[x]=-3,那么x的取值范围是( )
A.-3≤x<-2
B.-3<x≤-2
C.-3<x<-2
D.-3≤x≤-2
答案:A
解析:解答:∵对于有理数x,符号[x]表示不大于x的最大整数,[x]=-3,
∴,
解得:-3≤x<-2.
故选:A.
分析:根据最大整数的定义即可求解.
14. 宁城县城区现行出租车的收费标准:起步价5元(即行驶距离不超过3千米都需付5元车费),超过3千米后,每增加1千米,加收1.5元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共付车费11元,那么甲地到乙地路程的最大值是( )
A.5千米
B.7千米
C.8千米
D.9千米
答案:B
解析:解答:依题意得:1.5(x-3)≤11-5,
x-3≤4,
x≤7.
因此甲地到乙地路程的最大值是7千米.
故选:B.
分析:本题可先用11减去5得到6,则1.5(x-3)≤6,解出x的值,取最大整数即为本题的解.
15. 已知非负数a,b,c满足条件a+b=7,c-a=5,设S=a+b+c的最大值为m,最小值为n,则m-n的值( )
A.5
B.6
C.7
D.8
答案:C
解析:解答:∵a,b,c为非负数;
∴S=a+b+c≥0;
又∵c-a=5;
∴c=a+5;
∴c≥5;
∵a+b=7;
∴S=a+b+c=7+c;
又∵c≥5;
∴c=5时S最小,即S最小=12,即n=12;
∵a+b=7;
∴a≤7;
∴S=a+b+c=7+c=7+a+5=12+a;
∴a=7时S最大,即S最大=19,即m=19;
∴m-n=19-12=7.
故选C.
分析:由于已知a,b,c为非负数,所以m.n一定≥0;根据a+b=7和c-a=5推出c的最小值与a的最大值;然后再根据a+b=7和c-a=5把S=a+b+c转化为只含a或c的代数式,从而确定其最大值与最小值.
二.填空题
16. 写出一个无解的一元一次不等式组为________.
答案:
解析:解答:根据不等式组解集的口诀:大大小小找不到(无解),
可写x≤2,x≥3,
即.
分析:由题意写出一个无解的一元一次不等式组主要考查,其简便求法就是用口诀求解,根据不等式组解集的口诀:大大小小找不到(无解),来写出一个无解的一元一次不等式组.
17. 试构造一个解为x<-1的一元一次不等式组________.
答案:
解析:解答: .
答案不唯一
分析:本题为开放性题,根据同小取小列不等式组即可.
18. 不等式组 的所有整数解是________.
答案:0,1
解析:解答:,
解不等式①得,,
解不等式②得,x≤1,
所以不等式组的解集为,
所以原不等式组的整数解是0,1.
故答案为:0,1.
分析:先求出两个不等式的解集,再求其公共解,然后写出范围内的整数即可.
19. 对于任意实数m.n,定义一种运运算m※n=mn-m-n+3,等式的右边是通常的加减和乘法运算,例如:3※5=3×5-3-5+3=10.请根据上述定义解决问题:若a<2※x<7,且解集中有两个整数解,则a的取值范围是________.
答案:4≤a<5
解析:解答:根据题意得:2※x=2x-2-x+3=x+1,
∵a<x+1<7,即a-1<x<6解集中有两个整数解,
∴a的范围为4≤a<5,
故答案为:4≤a<5.
分析:利用题中的新定义化简所求不等式,求出a的范围即可.
20. 将不足40只鸡放入若干个笼中,若每个笼里放4只,则有一只鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,且最后一笼不足3只.则有鸡________只.
答案:37
解析:解答:设笼有x个.
,
解得:8<x<11
x=9时,4×9+1=37
x=10时,4×10+1=41(舍去).
故笼有9个,鸡有37只.
故答案是:37.
分析:设笼有x个,那么鸡就有(4x+1)只,根据若每个笼里放5只,则有一笼无鸡可放,且最后一笼不足3只,可列出不等式求解.
三.解答题
21. 解不等式组:,并求它的整数解的和.
答案:解答:由①得x>-2
由②得x≤1
∴不等式组的解集为-2<x≤1
∴不等式组的整数解的和为-1+0+1=0.
解析:分析:先求出不等式组中每个不等式的解集,然后求出其公共解集,进而求其整数解,最后求它的整数解的和即可.
22. 求不等式组的整数解.
答案:解答:
解不等式①,得 x>-2,
解不等式②,得 x<1.
不等式组的解集为-2<x<1,
所以原不等式组的整数解为-1,0.
解析:分析:首先求出不等式组中每一个不等式的解集,再根据大小小大中间找确定不等式组的解集即可.
23. 若不等式的整数解有5个,则m的取值范围是多少?
答案:解答:,
由①得:x>3,
由②得:x<m+1,
∴3<x<m+1,
∵不等式组有5个整数解,即:4.5.6.7.8,
∴8<m+1≤9,
∴7<m≤8,
答案为7<m≤8.
解析:分析:认真审题,首先用含有m的代数式表示出x的取值范围,再根据整数解的个数,即可求出本题的答案.
24. 解不等式组,并求它的整数解.
答案:解答:由①得:2x+4≤5x+10,
∴-3x≤6,
∴x≥-2.
由②得:,
∴x<3.
所以原不等式组的解集为-2≤x<3.
所以原不等式组的整数解为-2,-1,0,1,2.
解析:分析:分别得出不等式的解集,进而得出不等式组的解集,即可得出不等式组的整数解.
25. 一个矩形,两边长分别为x和15,如果它的周长小于60,面积大于195,求x的值.(长和宽都为正整数)
答案:解答:根据题意得:,
解得:13<x<15,
由x为正整数,得到x=14,
则x的值为14.
解析:分析:根据周长小于60,面积大于195列出不等式组,求出不等式组的解集,找出解集中的正整数解即可确定出x的值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 11 页 (共 12 页) 版权所有@21世纪教育网
