河南省驻马店市新蔡县第一高级中学2024-2025学年高一下学期4月月考数学试题(含解析)
文档属性
| 名称 | 河南省驻马店市新蔡县第一高级中学2024-2025学年高一下学期4月月考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 917.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 11:14:15 | ||
图片预览




文档简介
河南省驻马店市新蔡县第一高级中学2024 2025学年高一下学期4月月考数学试题
一、单选题
1.设钟摆每经过1.8秒回到原来的位置,在图中钟摆达到最高位置A点时开始计时,经过1分钟后,钟摆的大致位置是()
A.点A处
B.点B处
C.O、A之间
D.O、B之间
2.的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.设集合,那么( )
A. B.
C. D.
4.若把某空间站运行轨道看作圆形轨道,距地球表面的距离取394千米,已知地球半径约为6370千米,则空间站绕地球每旋转弧度,飞行的路程约为(取)( )
A.3300千米 B.3334千米 C.3540千米 D.3640千米
5.已知,那么( )
A. B. C. D.
6.若函数的图象关于坐标原点对称,则( )
A.1 B.2 C.3 D.4
7.已知函数的部分图象如图所示,下列说法不正确的是( )
A., B.函数的图象关于直线对称
C.函数的图象关于对称 D.函数在上单调递增
8.如图,“六芒星”是由两个边长为正三角形组成,中心重合于点且三组对边分别平行,点,是“六芒星”(如图)的两个顶点,动点在“六芒星”上(内部以及边界),则的取值范围是( )
A. B. C. D.
二、多选题
9.下列说法中正确的是( )
A.若,,且与共线,则
B.若,,且,则与不共线
C.若、、三点共线,则向量都是共线向量
D.若向量,且,则
10.函数的部分图象可能为( )
A. B.
C. D.
11.已知向量 的夹角为 , , , ,则( )
A. 在 方向上的投影向量的模为1 B. 在 方向上的投影向量的模为
C. 的最小值为 D. 取得最小值时,
三、填空题
12.已知,,则 .
13.已知在平行四边形ABCD中,,过点B作于点E,则的取值范围为 .
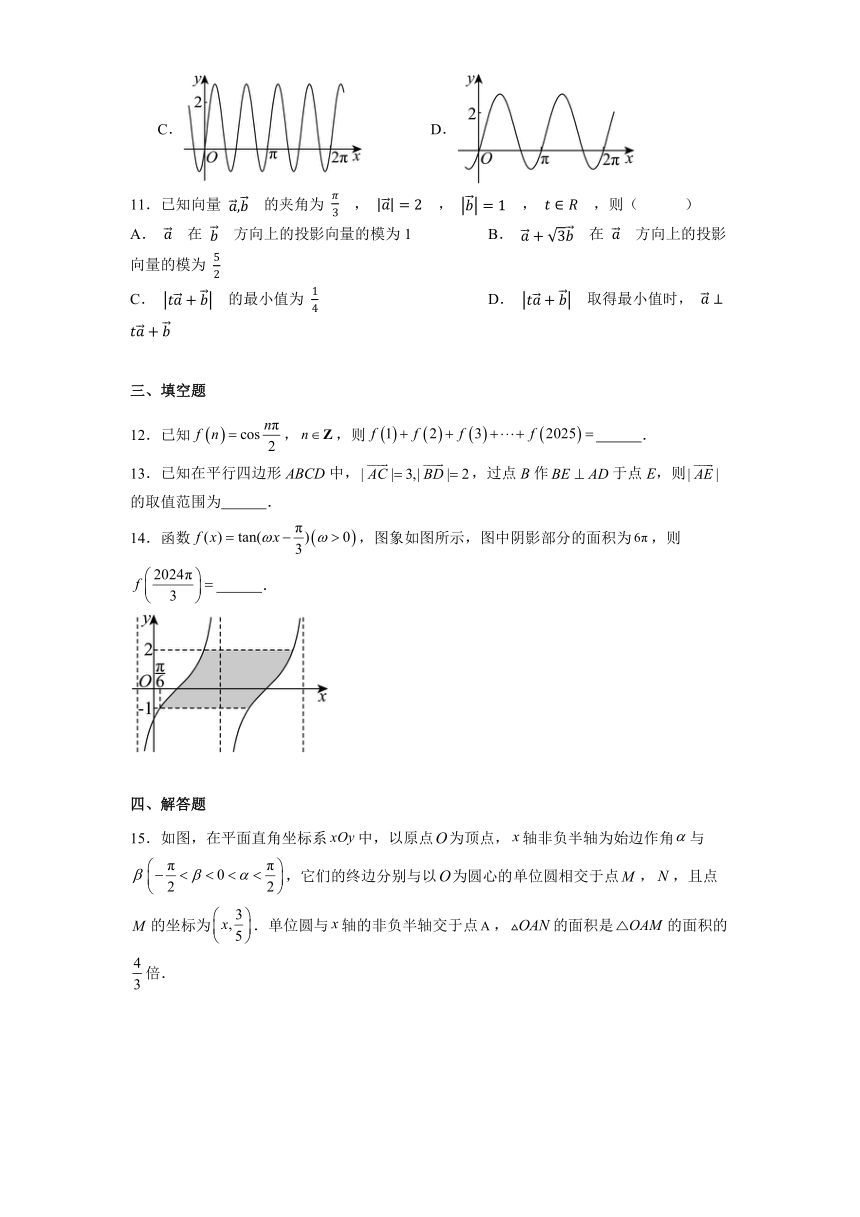
14.函数,图象如图所示,图中阴影部分的面积为,则 .
四、解答题
15.如图,在平面直角坐标系中,以原点为顶点,轴非负半轴为始边作角与,它们的终边分别与以为圆心的单位圆相交于点,,且点的坐标为.单位圆与轴的非负半轴交于点,的面积是的面积的倍.
(1)求的值;
(2)求的值.
16.(1)已知角顶点与坐标原点重合,始边与轴的非负半轴重合,终边过点.
求值:(ⅰ);
(ⅱ)
(2)若,求的值.
17.已知,,且与的夹角为60°.
(1)求的值
(2)求的值;
(3)若向量与平行,求实数的值.
18.如图,、、分别是三边、、上的点,且满足,设,.
(1)用、表示;
(2)已知点是的重心,用、表示.
19.已知函数满足,若将的图象上每个点先向左平移个单位长度,再向上平移个单位长度,所得的函数为偶函数.
(1)求的解析式;
(2)若对于任意的,总存在,使不等式成立,求实数的取值范围;
(3)若函数的图象在区间上至少含有20个零点,在所有满足条件的区间上,求的最小值.
参考答案
1.【答案】D
【详解】钟摆的周期T=1.8秒,1分钟=(33×1.8+0.6)秒,
又,所以经过1分钟后,钟摆在O、B之间.
故选D
2.【答案】B
【详解】因为,易知的终边在第二象限,
故角的终边在第二象限.
故选B.
3.【答案】C
【详解】由题意得
,
即M是由的奇数倍构成的集合,
又
,
即N是由的整数倍构成的集合,
则,
故选C.
4.【答案】C
【详解】空间站绕地球飞行的半径为(千米),
所以空间站绕地球每旋转弧度,飞行的路程约为(千米).
故选C.
5.【答案】B
【详解】因为,
所以.
故选B.
6.【答案】A
【详解】因为函数为偶函数且函数为奇函数,
所以为奇函数,即,
可得,则,
整理得,所以且,解得.
故选A.
7.【答案】B
【详解】对于A,由题意,,则,
则,
又在上,则,即,
所以,则,
又,所以,所以,即,,故A正确;
对于B,因为,
所以不是图象的对称轴,故B错误;
对于C,因为,
所以的图象关于点对称,故C正确;
对于D,当时,,
所以在上单调递增,故D正确.
故选B.
8.【答案】B
【详解】由对称性可得,连接,与的交点为,
则为的中点,为的中点,
故,,,,
过点作直线的垂线,垂足记为,
则向量在向量上的投影向量为,
所以,
如图过点作,,垂足分别为,
所以,,
观察图象可得,其中与同向,与反向,
所以当点位于点的位置时,取最大值,最大值为,
当点位于点的位置时,取最小值,最小值为,
所以的取值范围是.
故选B.
9.【答案】BCD
【详解】对于A,或 时,比例式无意义,故A错误;
对于B,若,, 与共线,则一定有,故B正确;
对于C,若、、三点共线,则,,在一条直线上,则,,都是共线向量,故C正确;
对于D,若向量,且,则,即,故D正确.
故选.
10.【答案】ABC
【详解】对于选项A,由图可知,的最小值为0,则,
当1时,,,的部分图象可以如选项A所示.
对于选项B,当时,的部分图象可以如选项B所示.
对于选项C,由,得,即,
当时,的部分图象可以如选项C所示.
对于选项D,由,得,即,
则,此时,排除D.
故选ABC
11.【答案】AD
【详解】由题意 在 方向上的投影向量的模为 ,故A说法正确;
在 方向上的投影向量的模为 ,故B说法错误;
,
当 时, 取得最小值 ,
此时 ,
所以 ,故C说法错误,D说法正确,
故选AD
12.【答案】
【详解】因为,,
则
13.【答案】
【详解】设,,则,,
因,则,
,
得,,
因,且不共线,则,则,
联立与,得,
解得,得, 则,
因,则,
故的取值范围为.
14.【答案】0
【详解】由图可知,,则,
所以.
15.【答案】(1),
(2)
【详解】(1)因为在单位圆上,且位于第一象限,
所以且,解得,所以,
所以,;
(2)因为的面积是的面积的倍,
所以,
又,所以,即,又,
解得或(舍去);
所以.
16.【答案】(1)(ⅰ),(ⅱ),(2)
【详解】(1)由于角的终边经过,
(ⅰ)故,
(ⅱ),
,
(2)
,
故,
17.【答案】(1)60
(2)
(3)
【详解】(1)因为,,
所以.
(2)因为,,且与的夹角为60°,
所以,
所以,
所以.
(3)因为向量与平行,所以,
由平面向量基本定理可得,
解得或,
所以的值为.
18.【答案】(1);
(2).
【详解】(1)因为,,,
所以,,
所以,
(2)由已知,
连接,其中点为线段的中点,点为线段的中点,
由已知,与的交点为重心,
由重心性质可得,故
所以,
又,
所以.
19.【答案】(1)
(2)
(3)
【详解】(1)因为,则,
所以函数的最小正周期为,则,则
将函数的图象上每个点先向左平移个单位长度,再向上平移个单位长度,
所得的函数为偶函数,则为偶函数,
所以,,可得,
因为,可得,所以;
(2)由(1)知,
由题意可知最大值应小于等于的最大值.
,,所以
所以,对于任意的恒成立
,所以,令,
则,
可得,由于,则,
令,则,设,
则
,
由于,故,
则在上单调递增,故的最大值为,
则的最小值为,
故.
(3)由题意知,即
故或,
解得或,
故的零点为或,
所以相邻两个零点之间的距离为或,
若最小,则和都是零点,此时在区间
分别恰有3,5,7,个零点,
所以在区间上恰有19个零点,
从而在区间上至少有一个零点,所以,所以.
一、单选题
1.设钟摆每经过1.8秒回到原来的位置,在图中钟摆达到最高位置A点时开始计时,经过1分钟后,钟摆的大致位置是()
A.点A处
B.点B处
C.O、A之间
D.O、B之间
2.的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.设集合,那么( )
A. B.
C. D.
4.若把某空间站运行轨道看作圆形轨道,距地球表面的距离取394千米,已知地球半径约为6370千米,则空间站绕地球每旋转弧度,飞行的路程约为(取)( )
A.3300千米 B.3334千米 C.3540千米 D.3640千米
5.已知,那么( )
A. B. C. D.
6.若函数的图象关于坐标原点对称,则( )
A.1 B.2 C.3 D.4
7.已知函数的部分图象如图所示,下列说法不正确的是( )
A., B.函数的图象关于直线对称
C.函数的图象关于对称 D.函数在上单调递增
8.如图,“六芒星”是由两个边长为正三角形组成,中心重合于点且三组对边分别平行,点,是“六芒星”(如图)的两个顶点,动点在“六芒星”上(内部以及边界),则的取值范围是( )
A. B. C. D.
二、多选题
9.下列说法中正确的是( )
A.若,,且与共线,则
B.若,,且,则与不共线
C.若、、三点共线,则向量都是共线向量
D.若向量,且,则
10.函数的部分图象可能为( )
A. B.
C. D.
11.已知向量 的夹角为 , , , ,则( )
A. 在 方向上的投影向量的模为1 B. 在 方向上的投影向量的模为
C. 的最小值为 D. 取得最小值时,
三、填空题
12.已知,,则 .
13.已知在平行四边形ABCD中,,过点B作于点E,则的取值范围为 .
14.函数,图象如图所示,图中阴影部分的面积为,则 .
四、解答题
15.如图,在平面直角坐标系中,以原点为顶点,轴非负半轴为始边作角与,它们的终边分别与以为圆心的单位圆相交于点,,且点的坐标为.单位圆与轴的非负半轴交于点,的面积是的面积的倍.
(1)求的值;
(2)求的值.
16.(1)已知角顶点与坐标原点重合,始边与轴的非负半轴重合,终边过点.
求值:(ⅰ);
(ⅱ)
(2)若,求的值.
17.已知,,且与的夹角为60°.
(1)求的值
(2)求的值;
(3)若向量与平行,求实数的值.
18.如图,、、分别是三边、、上的点,且满足,设,.
(1)用、表示;
(2)已知点是的重心,用、表示.
19.已知函数满足,若将的图象上每个点先向左平移个单位长度,再向上平移个单位长度,所得的函数为偶函数.
(1)求的解析式;
(2)若对于任意的,总存在,使不等式成立,求实数的取值范围;
(3)若函数的图象在区间上至少含有20个零点,在所有满足条件的区间上,求的最小值.
参考答案
1.【答案】D
【详解】钟摆的周期T=1.8秒,1分钟=(33×1.8+0.6)秒,
又,所以经过1分钟后,钟摆在O、B之间.
故选D
2.【答案】B
【详解】因为,易知的终边在第二象限,
故角的终边在第二象限.
故选B.
3.【答案】C
【详解】由题意得
,
即M是由的奇数倍构成的集合,
又
,
即N是由的整数倍构成的集合,
则,
故选C.
4.【答案】C
【详解】空间站绕地球飞行的半径为(千米),
所以空间站绕地球每旋转弧度,飞行的路程约为(千米).
故选C.
5.【答案】B
【详解】因为,
所以.
故选B.
6.【答案】A
【详解】因为函数为偶函数且函数为奇函数,
所以为奇函数,即,
可得,则,
整理得,所以且,解得.
故选A.
7.【答案】B
【详解】对于A,由题意,,则,
则,
又在上,则,即,
所以,则,
又,所以,所以,即,,故A正确;
对于B,因为,
所以不是图象的对称轴,故B错误;
对于C,因为,
所以的图象关于点对称,故C正确;
对于D,当时,,
所以在上单调递增,故D正确.
故选B.
8.【答案】B
【详解】由对称性可得,连接,与的交点为,
则为的中点,为的中点,
故,,,,
过点作直线的垂线,垂足记为,
则向量在向量上的投影向量为,
所以,
如图过点作,,垂足分别为,
所以,,
观察图象可得,其中与同向,与反向,
所以当点位于点的位置时,取最大值,最大值为,
当点位于点的位置时,取最小值,最小值为,
所以的取值范围是.
故选B.
9.【答案】BCD
【详解】对于A,或 时,比例式无意义,故A错误;
对于B,若,, 与共线,则一定有,故B正确;
对于C,若、、三点共线,则,,在一条直线上,则,,都是共线向量,故C正确;
对于D,若向量,且,则,即,故D正确.
故选.
10.【答案】ABC
【详解】对于选项A,由图可知,的最小值为0,则,
当1时,,,的部分图象可以如选项A所示.
对于选项B,当时,的部分图象可以如选项B所示.
对于选项C,由,得,即,
当时,的部分图象可以如选项C所示.
对于选项D,由,得,即,
则,此时,排除D.
故选ABC
11.【答案】AD
【详解】由题意 在 方向上的投影向量的模为 ,故A说法正确;
在 方向上的投影向量的模为 ,故B说法错误;
,
当 时, 取得最小值 ,
此时 ,
所以 ,故C说法错误,D说法正确,
故选AD
12.【答案】
【详解】因为,,
则
13.【答案】
【详解】设,,则,,
因,则,
,
得,,
因,且不共线,则,则,
联立与,得,
解得,得, 则,
因,则,
故的取值范围为.
14.【答案】0
【详解】由图可知,,则,
所以.
15.【答案】(1),
(2)
【详解】(1)因为在单位圆上,且位于第一象限,
所以且,解得,所以,
所以,;
(2)因为的面积是的面积的倍,
所以,
又,所以,即,又,
解得或(舍去);
所以.
16.【答案】(1)(ⅰ),(ⅱ),(2)
【详解】(1)由于角的终边经过,
(ⅰ)故,
(ⅱ),
,
(2)
,
故,
17.【答案】(1)60
(2)
(3)
【详解】(1)因为,,
所以.
(2)因为,,且与的夹角为60°,
所以,
所以,
所以.
(3)因为向量与平行,所以,
由平面向量基本定理可得,
解得或,
所以的值为.
18.【答案】(1);
(2).
【详解】(1)因为,,,
所以,,
所以,
(2)由已知,
连接,其中点为线段的中点,点为线段的中点,
由已知,与的交点为重心,
由重心性质可得,故
所以,
又,
所以.
19.【答案】(1)
(2)
(3)
【详解】(1)因为,则,
所以函数的最小正周期为,则,则
将函数的图象上每个点先向左平移个单位长度,再向上平移个单位长度,
所得的函数为偶函数,则为偶函数,
所以,,可得,
因为,可得,所以;
(2)由(1)知,
由题意可知最大值应小于等于的最大值.
,,所以
所以,对于任意的恒成立
,所以,令,
则,
可得,由于,则,
令,则,设,
则
,
由于,故,
则在上单调递增,故的最大值为,
则的最小值为,
故.
(3)由题意知,即
故或,
解得或,
故的零点为或,
所以相邻两个零点之间的距离为或,
若最小,则和都是零点,此时在区间
分别恰有3,5,7,个零点,
所以在区间上恰有19个零点,
从而在区间上至少有一个零点,所以,所以.
同课章节目录
