华师大版七年级数学下册第九章多边形第1节三角形2三角形的内角和与外角和
文档属性
| 名称 | 华师大版七年级数学下册第九章多边形第1节三角形2三角形的内角和与外角和 |
|
|
| 格式 | doc | ||
| 文件大小 | 205.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-21 11:58:35 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学七年级下册第九章第一节9.1.2三角形的内角和与外角和
同步练习
一.选择题
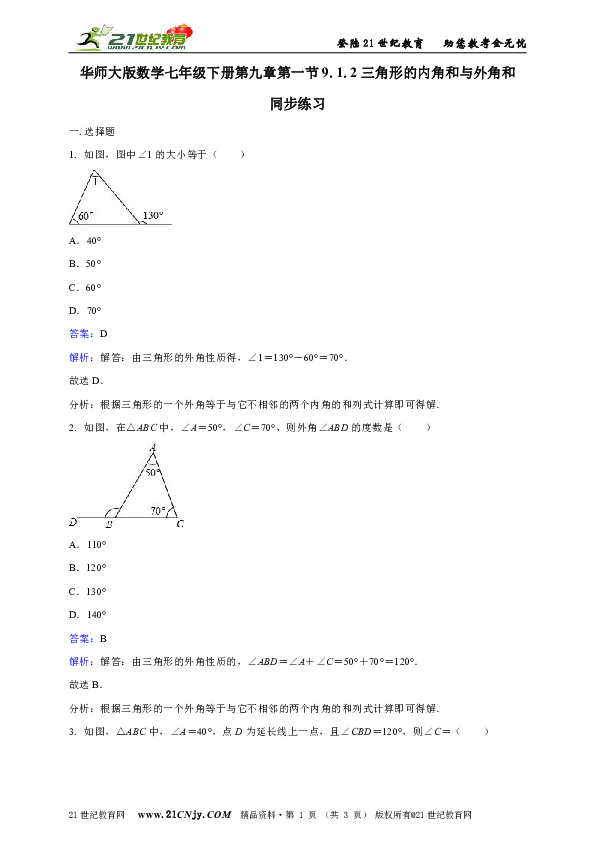
1. 如图,图中∠1的大小等于( )
A.40°
B.50°
C.60°
D.70°
答案:D
解析:解答:由三角形的外角性质得,∠1=130°-60°=70°.
故选D.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
2. 如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是( )
A.110°
B.120°
C.130°
D.140°
答案:B
解析:解答:由三角形的外角性质的,∠ABD=∠A+∠C=50°+70°=120°.
故选B.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
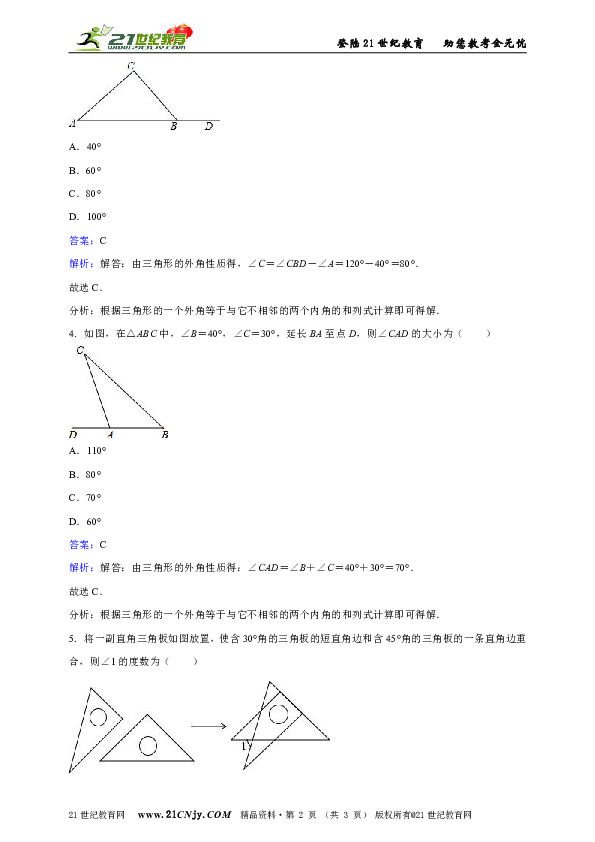
3. 如图,△ABC中,∠A=40°,点D为延长线上一点,且∠CBD=120°,则∠C=( )
A.40°
B.60°
C.80°
D.100°
答案:C
解析:解答:由三角形的外角性质得,∠C=∠CBD-∠A=120°-40°=80°.
故选C.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
4. 如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )
A.110°
B.80°
C.70°
D.60°
答案:C
解析:解答:由三角形的外角性质得:∠CAD=∠B+∠C=40°+30°=70°.
故选C.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
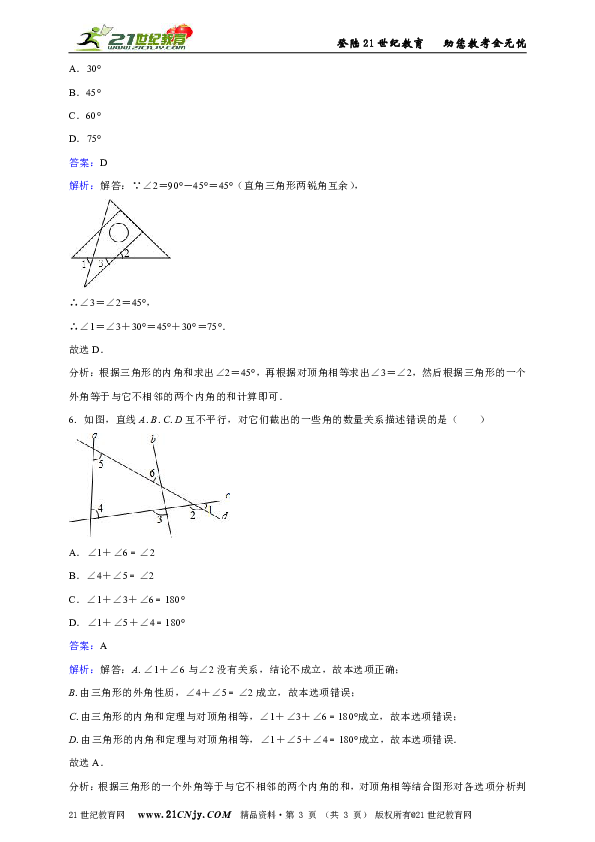
5. 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
A.30°
B.45°
C.60°
D.75°
答案:D
解析:解答:∵∠2=90°-45°=45°(直角三角形两锐角互余),
∴∠3=∠2=45°,
∴∠1=∠3+30°=45°+30°=75°.
故选D.
分析:根据三角形的内角和求出∠2=45°,再根据对顶角相等求出∠3=∠2,然后根据三角形的一个外角等于与它不相邻的两个内角的和计算即可.
6. 如图,直线A.B.C.D互不平行,对它们截出的一些角的数量关系描述错误的是( )
A.∠1+∠6﹦∠2
B.∠4+∠5﹦∠2
C.∠1+∠3+∠6﹦180°
D.∠1+∠5+∠4﹦180°
答案:A
解析:解答:A.∠1+∠6与∠2没有关系,结论不成立,故本选项正确;
B.由三角形的外角性质,∠4+∠5﹦∠2成立,故本选项错误;
C.由三角形的内角和定理与对顶角相等,∠1+∠3+∠6﹦180°成立,故本选项错误;
D.由三角形的内角和定理与对顶角相等,∠1+∠5+∠4﹦180°成立,故本选项错误.
故选A.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和,对顶角相等结合图形对各选项分析判断利用排除法求解.
7. 将两个含30°和45°的直角三角板如图放置,则∠α的度数是( )
A.10°
B.15°
C.20°
D.25°
答案:B
解析:解答:由三角形的外角性质得,∠α=60°-45°=15°.
故选B.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
8. 如图,在△ABC中,D是BC上延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
A.20°
B.30°
C.70°
D.80°
答案:D
解析:解答:由三角形的外角性质得,∠A=120°-40°=80°.
故选D.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
9. 如图,已知∠A=33°,∠B=75°,点C在直线AD上,则∠BCD为( )
A.147°
B.108°
C.105°
D.以上答案都不对
答案:B
解析:解答:∵∠BCD是△ABC的外角,∠A=33°,∠B=75°,
∴∠BCD=∠A+∠B=33°+75°=108°.
故选:B.
分析:利用三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和,解答即可.
10. 如图,一副分别含有30°和45°角的两个直角三角板,拼成如图,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )
A.15°
B.25°
C.30°
D.10°
答案:A
解析:解答:∵∠C=90°,∠E=30°,
∴∠CDE=90°-30°=60°,
由三角形的外角性质得,∠CDE=∠B+∠BFD,
∴60°=45°+∠BFD,
解得∠BFD=15°.
故选A.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CDE=∠B+∠BFD,然后代入数据进行计算即可得解.
11. 已知,如图,△ABC中,∠B=∠DAC,则∠BAC和∠ADC的关系是( )
A.∠BAC<∠ADC
B.∠BAC=∠ADC
C.∠BAC>∠ADC
D.不能确定
答案:B
解析:解答:由三角形的外角性质,∠ADC=∠B+∠BAD,
∵∠BAC=∠BAD+∠DAC,∠B=∠DAC,
∴∠BAC=∠ADC.
故选B.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADC=∠B+∠BAD,再根据∠BAC=∠BAD+∠DAC即可得解.
12. 如图所示:D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的关系描述正确的是( )
A.∠A<∠1<2
B.∠2<∠1<∠A
C.∠1>∠2>∠A
D.无法确定
答案:A
解析:解答:∵∠2=∠1+∠DCE,∠1=∠A+∠ABD,
∴∠2>∠1>∠A,
故选A.
分析:根据三角形外角的性质可得出∠2=∠1+∠DCE,∠1=∠A+∠ABD,从而得出结论即可.
13. 三角形的所有外角(每个顶点只取一个外角)中,锐角最多有( )
A.0个
B.1个
C.2个
D.3个
答案:B
解析:解答:∵三角形的内角最多有1个钝角,
∴三角形的三个外角中,锐角最多有1个.
故选B.
分析:因为三角形的内角中钝角最多有1个,所以根据平角的定义可以得知三角形的外角中最多有1个锐角.
14. 如图,平面上直线A.B分别过线段AB两端点(数据如图),则A.B相交所成的锐角是( )
A.20°
B.30°
C.80°
D.100°
答案:A
解析:解答:A,B相交所成的锐角=100°-80°=20°.
故选:A.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
15. 如图,若∠1=100°,∠C=70°,则∠A的度数为( )
A.20°
B.30°
C.70°
D.80°
答案:B
解析:解答:∵∠1=∠A+∠C,
∴∠A=∠1-∠C=100°-70°=30°,
故选B.
分析:直接根据三角形的外角等于与其不相邻的两个内角的和求解即可.
二.填空题
16. 如图,平面上直线A,B分别经过线段OK两端点(数据如图),则A,B相交所成的锐角是______.
答案:30°
解析:解答:由三角形的外角性质得,A,B相交所成的锐角的度数是100°-70°=30°.
故答案为:30°.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
17. 如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是_____度.
答案:60
解析:解答:∵∠ACD=∠B+∠A,
而∠A=80°,∠B=4°,
∴∠ACD=80°+40°=120°.
∵CE平分∠ACD,
∴∠ACE=60°,
故答案为60.
分析:由∠A=80°,∠B=40°,根据三角形任意一个外角等于与之不相邻的两内角的和得到∠ACD=∠B+∠A,然后利用角平分线的定义计算即可.
18. 如图,∠A+∠B+∠C+∠D+∠E的度数为_____度.
答案:180
解析:解答:如图连接CE,
根据三角形的外角性质得∠1=∠A+∠B=∠2+∠3,
在△DCE中有,∠D+∠2+∠DCB+∠3+∠AED=180°,
∴∠D+∠A+∠DCB+∠B+∠AED=180°.
分析:如图连接CE,根据三角形的一个外角等于和它不相邻的两个内角和∠1=∠A+∠B=∠2+∠3,在△DCE中有∠D+∠2+∠DCB+∠3+∠AED=180°,即可得∠D+∠A+∠DCB+∠B+∠AED=180°.
19. 如图,一副三角板△AOC和△BCD如图摆放,则∠AOB=________.
答案:165°
解析:解答:∵∠BDC=60°,
∴∠ADO=180°-∠BDC=120°,
∴∠OAD=45°,
∴∠AOB=∠OAD+∠ADO=165°.
故答案为:165°.
分析:根据邻补角求出∠ADO的度数,再利用外角的性质,即可解答.
20. 如图,已知△ABC为直角三角形,∠B=90°,若沿图中虚线剪去∠B,则∠1+∠2等于_____度.
答案:270
解析:解答:∵△ABC为直角三角形,∠B=90,
∴∠1=90°+∠BNM,∠2=90°+∠BMN,
∴∠1+∠2=270°.
故答案为:270.
分析:如图,根据题意可知∠1=90°+∠BNM,∠2=90°+∠BMN,然后结合三角形内角和定理即可推出∠1+∠2的度数.
三.解答题
21. 如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB.BE于D.F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB.BE的延长线于D.F两点,试探究(1)中结论是否仍成立?为什么?
答案:解答:(1)∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC;
(2)探究(1)中结论仍成立;
理由:∵AD平分∠BAG,
∴∠BAD=∠GAD,
∵∠FAE=∠GAD,
∴∠FAE=∠BAD,
∵∠EFD=∠AEB-∠FAE,∠ADC=∠ABC-∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC.
解析:分析:(1)首先根据角平分线的性质可得∠BAD=∠DAC,再根据内角与外角的性质可得∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,进而得到∠EFD=∠ADC;
(2)首先根据角平分线的性质可得∠BAD=∠DAG,再根据等量代换可得∠FAE=∠BAD,然后再根据内角与外角的性质可得∠EFD=∠AEB-∠FAE,∠ADC=∠ABC-∠BAD,进而得∠EFD=∠ADC.
22. 一个零件的形状如图,按规定∠A应等于90°,∠B.∠C应分别是21°和32°,现测量得∠BDC=148°,你认为这个零件合格吗?为什么?
答案:解答:延长CD与AB相交于点F.
∵∠DFB=∠C+∠A=32°+90°=122°,
又∵∠BDC=∠DFB+∠B=122°+21°=143°,
∵实际量得的∠BDC=148°,
143°≠148°,
∴这个零件不合格.
解析:分析:直接利用图形中的外角和等于与它不相邻的两个内角和求解.
23. 如图,AD是△ABC的角平分线,∠B=45°,∠ADC=75°,求∠BAC.∠C的度数.
答案:解答:∵∠B=45°,∠ADC=75°,
∴∠BAD=∠ADC-∠B=75°-45°=30°,
∵AD是△ABC的角平分线,
∴∠BAC=2∠BAD=2×30°=60°,
在△ABC中,∠C=180°-∠BAC-∠B=180°-60°-45°=75°.
解析:分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BAD,再根据角平分线的定义可得∠BAC=2∠BAD,然后利用三角形的内角和定理列式计算即可求出∠C.
24. 如图,点D是△ABC的边BC上的一点,∠B=∠BAD=∠C,∠ADC=72°.
试求∠DAC的度数.
答案:解答:∵∠ADC是△ABD的外角,∠ADC=72°,
∴∠ADC=∠B+∠BAD.
又∵∠B=∠BAD,
∴∠B=∠BAD=36°.
∵∠B=∠BAD=∠C,
∴∠C=36°.
在△ADC中,
∵∠DAC+∠ADC+∠C=180°
∴∠DAC=180°-∠ADC-∠C
=180°-72°-36°
=72°.
解析:分析:先根据三角形外角的性质得出∠ADC=∠B+∠BAD,再由∠B=∠BAD可知∠B=∠BAD=36°,在△ADC中,根据三角形内角和定理即可得出结论.
25. 如图,在△ABC中,D是BC边上一点,∠1=∠B,∠2=∠C,∠BAC=63°,求∠CAD的度数.
答案:解答:∵∠2是△ADB的一个外角,
∴∠2=∠1+∠B,
∵∠1=∠B,∴∠2=2∠1,
∵∠2=∠C,∴∠C=2∠1,
∴∠BAC=180°-3∠1
∵∠BAC=63°,
∴∠1=39°,
∴∠CAD=24°.
解析:分析:根据三角形的一个外角等于与它不相邻的两个内角的和得到∠C=2∠1,根据三角形内角和定理列出算式,求出答案.
21世纪教育网 www.21CNjy.COM 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21CNjy.COM 精品资料·第 13 页 (共 13 页) 版权所有@21世纪教育网
华师大版数学七年级下册第九章第一节9.1.2三角形的内角和与外角和
同步练习
一.选择题
1. 如图,图中∠1的大小等于( )
A.40°
B.50°
C.60°
D.70°
答案:D
解析:解答:由三角形的外角性质得,∠1=130°-60°=70°.
故选D.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
2. 如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是( )
A.110°
B.120°
C.130°
D.140°
答案:B
解析:解答:由三角形的外角性质的,∠ABD=∠A+∠C=50°+70°=120°.
故选B.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
3. 如图,△ABC中,∠A=40°,点D为延长线上一点,且∠CBD=120°,则∠C=( )
A.40°
B.60°
C.80°
D.100°
答案:C
解析:解答:由三角形的外角性质得,∠C=∠CBD-∠A=120°-40°=80°.
故选C.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
4. 如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )
A.110°
B.80°
C.70°
D.60°
答案:C
解析:解答:由三角形的外角性质得:∠CAD=∠B+∠C=40°+30°=70°.
故选C.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
5. 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
A.30°
B.45°
C.60°
D.75°
答案:D
解析:解答:∵∠2=90°-45°=45°(直角三角形两锐角互余),
∴∠3=∠2=45°,
∴∠1=∠3+30°=45°+30°=75°.
故选D.
分析:根据三角形的内角和求出∠2=45°,再根据对顶角相等求出∠3=∠2,然后根据三角形的一个外角等于与它不相邻的两个内角的和计算即可.
6. 如图,直线A.B.C.D互不平行,对它们截出的一些角的数量关系描述错误的是( )
A.∠1+∠6﹦∠2
B.∠4+∠5﹦∠2
C.∠1+∠3+∠6﹦180°
D.∠1+∠5+∠4﹦180°
答案:A
解析:解答:A.∠1+∠6与∠2没有关系,结论不成立,故本选项正确;
B.由三角形的外角性质,∠4+∠5﹦∠2成立,故本选项错误;
C.由三角形的内角和定理与对顶角相等,∠1+∠3+∠6﹦180°成立,故本选项错误;
D.由三角形的内角和定理与对顶角相等,∠1+∠5+∠4﹦180°成立,故本选项错误.
故选A.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和,对顶角相等结合图形对各选项分析判断利用排除法求解.
7. 将两个含30°和45°的直角三角板如图放置,则∠α的度数是( )
A.10°
B.15°
C.20°
D.25°
答案:B
解析:解答:由三角形的外角性质得,∠α=60°-45°=15°.
故选B.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
8. 如图,在△ABC中,D是BC上延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
A.20°
B.30°
C.70°
D.80°
答案:D
解析:解答:由三角形的外角性质得,∠A=120°-40°=80°.
故选D.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
9. 如图,已知∠A=33°,∠B=75°,点C在直线AD上,则∠BCD为( )
A.147°
B.108°
C.105°
D.以上答案都不对
答案:B
解析:解答:∵∠BCD是△ABC的外角,∠A=33°,∠B=75°,
∴∠BCD=∠A+∠B=33°+75°=108°.
故选:B.
分析:利用三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和,解答即可.
10. 如图,一副分别含有30°和45°角的两个直角三角板,拼成如图,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )
A.15°
B.25°
C.30°
D.10°
答案:A
解析:解答:∵∠C=90°,∠E=30°,
∴∠CDE=90°-30°=60°,
由三角形的外角性质得,∠CDE=∠B+∠BFD,
∴60°=45°+∠BFD,
解得∠BFD=15°.
故选A.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CDE=∠B+∠BFD,然后代入数据进行计算即可得解.
11. 已知,如图,△ABC中,∠B=∠DAC,则∠BAC和∠ADC的关系是( )
A.∠BAC<∠ADC
B.∠BAC=∠ADC
C.∠BAC>∠ADC
D.不能确定
答案:B
解析:解答:由三角形的外角性质,∠ADC=∠B+∠BAD,
∵∠BAC=∠BAD+∠DAC,∠B=∠DAC,
∴∠BAC=∠ADC.
故选B.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADC=∠B+∠BAD,再根据∠BAC=∠BAD+∠DAC即可得解.
12. 如图所示:D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的关系描述正确的是( )
A.∠A<∠1<2
B.∠2<∠1<∠A
C.∠1>∠2>∠A
D.无法确定
答案:A
解析:解答:∵∠2=∠1+∠DCE,∠1=∠A+∠ABD,
∴∠2>∠1>∠A,
故选A.
分析:根据三角形外角的性质可得出∠2=∠1+∠DCE,∠1=∠A+∠ABD,从而得出结论即可.
13. 三角形的所有外角(每个顶点只取一个外角)中,锐角最多有( )
A.0个
B.1个
C.2个
D.3个
答案:B
解析:解答:∵三角形的内角最多有1个钝角,
∴三角形的三个外角中,锐角最多有1个.
故选B.
分析:因为三角形的内角中钝角最多有1个,所以根据平角的定义可以得知三角形的外角中最多有1个锐角.
14. 如图,平面上直线A.B分别过线段AB两端点(数据如图),则A.B相交所成的锐角是( )
A.20°
B.30°
C.80°
D.100°
答案:A
解析:解答:A,B相交所成的锐角=100°-80°=20°.
故选:A.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
15. 如图,若∠1=100°,∠C=70°,则∠A的度数为( )
A.20°
B.30°
C.70°
D.80°
答案:B
解析:解答:∵∠1=∠A+∠C,
∴∠A=∠1-∠C=100°-70°=30°,
故选B.
分析:直接根据三角形的外角等于与其不相邻的两个内角的和求解即可.
二.填空题
16. 如图,平面上直线A,B分别经过线段OK两端点(数据如图),则A,B相交所成的锐角是______.
答案:30°
解析:解答:由三角形的外角性质得,A,B相交所成的锐角的度数是100°-70°=30°.
故答案为:30°.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
17. 如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是_____度.
答案:60
解析:解答:∵∠ACD=∠B+∠A,
而∠A=80°,∠B=4°,
∴∠ACD=80°+40°=120°.
∵CE平分∠ACD,
∴∠ACE=60°,
故答案为60.
分析:由∠A=80°,∠B=40°,根据三角形任意一个外角等于与之不相邻的两内角的和得到∠ACD=∠B+∠A,然后利用角平分线的定义计算即可.
18. 如图,∠A+∠B+∠C+∠D+∠E的度数为_____度.
答案:180
解析:解答:如图连接CE,
根据三角形的外角性质得∠1=∠A+∠B=∠2+∠3,
在△DCE中有,∠D+∠2+∠DCB+∠3+∠AED=180°,
∴∠D+∠A+∠DCB+∠B+∠AED=180°.
分析:如图连接CE,根据三角形的一个外角等于和它不相邻的两个内角和∠1=∠A+∠B=∠2+∠3,在△DCE中有∠D+∠2+∠DCB+∠3+∠AED=180°,即可得∠D+∠A+∠DCB+∠B+∠AED=180°.
19. 如图,一副三角板△AOC和△BCD如图摆放,则∠AOB=________.
答案:165°
解析:解答:∵∠BDC=60°,
∴∠ADO=180°-∠BDC=120°,
∴∠OAD=45°,
∴∠AOB=∠OAD+∠ADO=165°.
故答案为:165°.
分析:根据邻补角求出∠ADO的度数,再利用外角的性质,即可解答.
20. 如图,已知△ABC为直角三角形,∠B=90°,若沿图中虚线剪去∠B,则∠1+∠2等于_____度.
答案:270
解析:解答:∵△ABC为直角三角形,∠B=90,
∴∠1=90°+∠BNM,∠2=90°+∠BMN,
∴∠1+∠2=270°.
故答案为:270.
分析:如图,根据题意可知∠1=90°+∠BNM,∠2=90°+∠BMN,然后结合三角形内角和定理即可推出∠1+∠2的度数.
三.解答题
21. 如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB.BE于D.F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB.BE的延长线于D.F两点,试探究(1)中结论是否仍成立?为什么?
答案:解答:(1)∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC;
(2)探究(1)中结论仍成立;
理由:∵AD平分∠BAG,
∴∠BAD=∠GAD,
∵∠FAE=∠GAD,
∴∠FAE=∠BAD,
∵∠EFD=∠AEB-∠FAE,∠ADC=∠ABC-∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC.
解析:分析:(1)首先根据角平分线的性质可得∠BAD=∠DAC,再根据内角与外角的性质可得∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,进而得到∠EFD=∠ADC;
(2)首先根据角平分线的性质可得∠BAD=∠DAG,再根据等量代换可得∠FAE=∠BAD,然后再根据内角与外角的性质可得∠EFD=∠AEB-∠FAE,∠ADC=∠ABC-∠BAD,进而得∠EFD=∠ADC.
22. 一个零件的形状如图,按规定∠A应等于90°,∠B.∠C应分别是21°和32°,现测量得∠BDC=148°,你认为这个零件合格吗?为什么?
答案:解答:延长CD与AB相交于点F.
∵∠DFB=∠C+∠A=32°+90°=122°,
又∵∠BDC=∠DFB+∠B=122°+21°=143°,
∵实际量得的∠BDC=148°,
143°≠148°,
∴这个零件不合格.
解析:分析:直接利用图形中的外角和等于与它不相邻的两个内角和求解.
23. 如图,AD是△ABC的角平分线,∠B=45°,∠ADC=75°,求∠BAC.∠C的度数.
答案:解答:∵∠B=45°,∠ADC=75°,
∴∠BAD=∠ADC-∠B=75°-45°=30°,
∵AD是△ABC的角平分线,
∴∠BAC=2∠BAD=2×30°=60°,
在△ABC中,∠C=180°-∠BAC-∠B=180°-60°-45°=75°.
解析:分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BAD,再根据角平分线的定义可得∠BAC=2∠BAD,然后利用三角形的内角和定理列式计算即可求出∠C.
24. 如图,点D是△ABC的边BC上的一点,∠B=∠BAD=∠C,∠ADC=72°.
试求∠DAC的度数.
答案:解答:∵∠ADC是△ABD的外角,∠ADC=72°,
∴∠ADC=∠B+∠BAD.
又∵∠B=∠BAD,
∴∠B=∠BAD=36°.
∵∠B=∠BAD=∠C,
∴∠C=36°.
在△ADC中,
∵∠DAC+∠ADC+∠C=180°
∴∠DAC=180°-∠ADC-∠C
=180°-72°-36°
=72°.
解析:分析:先根据三角形外角的性质得出∠ADC=∠B+∠BAD,再由∠B=∠BAD可知∠B=∠BAD=36°,在△ADC中,根据三角形内角和定理即可得出结论.
25. 如图,在△ABC中,D是BC边上一点,∠1=∠B,∠2=∠C,∠BAC=63°,求∠CAD的度数.
答案:解答:∵∠2是△ADB的一个外角,
∴∠2=∠1+∠B,
∵∠1=∠B,∴∠2=2∠1,
∵∠2=∠C,∴∠C=2∠1,
∴∠BAC=180°-3∠1
∵∠BAC=63°,
∴∠1=39°,
∴∠CAD=24°.
解析:分析:根据三角形的一个外角等于与它不相邻的两个内角的和得到∠C=2∠1,根据三角形内角和定理列出算式,求出答案.
21世纪教育网 www.21CNjy.COM 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21CNjy.COM 精品资料·第 13 页 (共 13 页) 版权所有@21世纪教育网
