【原创】北师大版八年级数学下册:3.2 图形的旋转(教案+配套学案)
文档属性
| 名称 | 【原创】北师大版八年级数学下册:3.2 图形的旋转(教案+配套学案) |

|
|
| 格式 | zip | ||
| 文件大小 | 356.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-18 15:29:15 | ||
图片预览



文档简介
第三章
图形的平移与旋转
第2节.图形的旋转(第1课时)
一、学生起点分析
学生在七年级下学期已经学习了“生活中的轴
( http: / / www.21cnjy.com )对称”一节,而且在本章的第一节,学生又经历了探索图形平移性质的过程,已经积累了相当的图形变换的数学活动经验,同时八年级学生逻辑思维从经验型逐步向理论型发展,观察能力、记忆能力和想象能力也在迅速发展,他们有强烈的独立思考、自主探索的愿望,这些对本节的学习都会有帮助。但旋转是三种变换中难度较大的一种,图形也比较复杂,因此,学生对旋转图形的形成过程的理解仍会有一定的困难。
二、教学任务分析
图形的旋转是继平移、轴对称之后的又一种图形基本变换,是义务教育阶段
数学课程标准中图形变换的一个重要组成部分。
( http: / / www.21cnjy.com )教材从学生实际接触、观察到的一些现象出发,从具体到抽象,从感性到理性,从实践到理论,再用理论检验实践,循序渐进地指导学生认识自然界和生活中的旋转,进而探索其性质。因此,旋转是培养学生思维能力、树立运动变化观点的良好素材;同时“图形的旋转”也为本章后续学习对称图形、中心对称图形做好准备,为今后学习“圆”的知识内容做好铺垫。
三、教学目标、重难点的确定
(一)教学目标
1、通过类比平移及其相关的定义,能够确定旋转及其相关的定义。
2、通过类比平移的性质,能够探究出旋转的性质。
(二)重难点
重点:类比平移与旋转的异同,掌握旋转的定义和基本性质,并利用数学知识解释生活中的旋转现象.
难点:探索旋转的性质,特别是,对应点到旋转中心的距离相等
四、学习过程
(一)、知识回顾,构建动场
HYPERLINK
"http://www.21cnjy.com"
同学们,上图是我们已经学过的两种图形变换。你知道分别是哪两种么?
师:同学们,在我们数学学习过程中有三大图形变换,前面我们已经学习了两种,请看屏幕。
这是?
(二)、自主学习,把握概念
师:很好,看来同学们对学过的内容掌握得非常的棒。
师:好,大家再来看这几个图,是不是我们学过的轴对称?是平移么?
既然他们既不是轴对称也不是平移,结合大屏幕中的动图,谈一谈这几个图有没有什么共同特征?将你的思考记录在学案上。
1、类比猜想:
( http: / / www.21cnjy.com )
结合大屏幕中的动图,谈一谈这几个例子有什么共同特征?将你的思考记录在学案上。
师:结合刚才同学们描述的三个方面,大家能不能描述一下点A是如何转动的呢?点B呢?线段oc呢?
我们把平面上能够具备这三方面转动的图形变换称为图形的旋转(板书)
这节课我们就一起来看一下图形的旋转
好,结合刚才的实例,大家把旋转的定义总结出来?找一个同学说一下。
好,刚才同学们总结出来的三个方面我们依据旋转的定义,分别称为……
大家回头再来看一下线段OC的旋转,如果老师在线段OC上取一点M,大家能描述一下点M是怎样运动的么?与线段OC的旋转是否相同?
2、总结结论:
(1)、旋转定义:
(2)、旋转的三要素:
、
、
。
师:根据上述定义,你能举出旋转的例子吗?
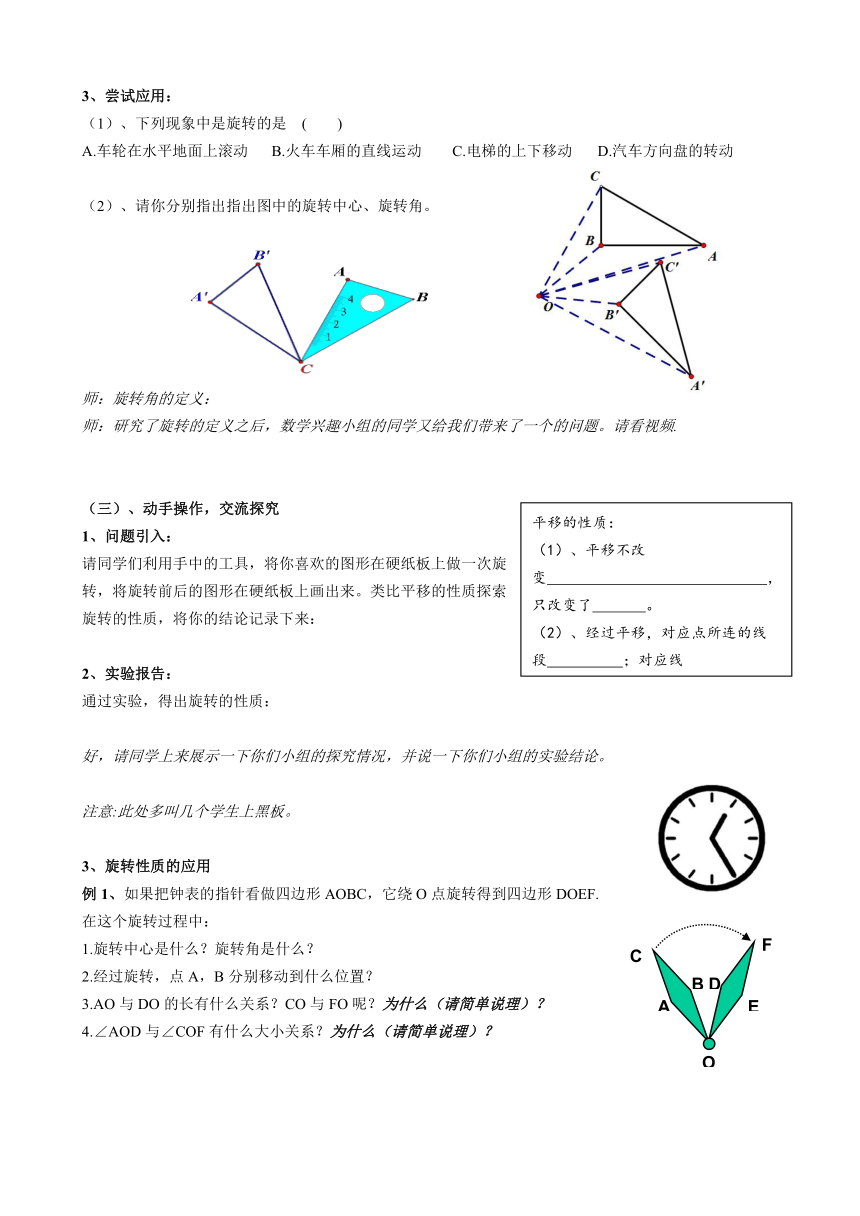
3、尝试应用:
(1)、下列现象中是旋转的是 ( )
A.车轮在水平地面上滚动
B.火车车厢的直线运动
C.电梯的上下移动
D.汽车方向盘的转动
(2)、请你分别指出指出图中的旋转中心、旋转角。
师:旋转角的定义:
师:研究了旋转的定义之后,数学兴趣小组的同学又给我们带来了一个的问题。请看视频.
(三)、动手操作,交流探究
1、问题引入:
请同学们利用手中的工具,将
( http: / / www.21cnjy.com )你喜欢的图形在硬纸板上做一次旋转,将旋转前后的图形在硬纸板上画出来。类比平移的性质探索旋转的性质,将你的结论记录下来:
2、实验报告:
通过实验,得出旋转的性质:
好,请同学上来展示一下你们小组的探究情况,并说一下你们小组的实验结论。
注意:此处多叫几个学生上黑板。
3、旋转性质的应用
例1、如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF.
在这个旋转过程中:
1.旋转中心是什么?旋转角是什么?
2.经过旋转,点A,B分别移动到什么位置?
3.AO与DO的长有什么关系?CO与FO呢?为什么(请简单说理)?
4.∠AOD与∠COF有什么大小关系?为什么(请简单说理)?
例2、△ABC是等边三角形,
△ABP顺时针旋转后能与△CBP’重合,那么:
(1)旋转中心是哪一点?
(2)旋转角是多少度?
(3)连结PP’后,△BPP’是什么三角形?
(四)、整体建构:
学生建构
教师建构
一种运动:图形的旋转,是一种运动;
两类思想:类比思想、转化思想;
三个要素:旋转中心,旋转方向,旋转角度;
四个性质:
①对应线段相等,对应角相等;
②对应点到旋转中心的距离相等;
③任意一对对应点与旋转中心的连线所成的角都等于旋转角;
④图形上的每一点都绕旋转中心沿相同方向转动了相同的角度.
(五)、当堂检测
A组:
1、
同学们曾玩过万花筒,它是由三块等
( http: / / www.21cnjy.com )宽等长的玻璃片围成的.如图是看到的万花筒的一个图案,图中所有小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以A为中心(
).
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
2、钟表的分针经过40分钟,它转过的角度是(
)
A.120° B.240° C.150° D.180°
B组:
3、
把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,
若∠A′DC=89°,求∠A的度数
C组:
4、如图,P是正三角形
ABC
内的一点,且PA=6,PB=8,PC=10.若将△PAC
绕点A逆时针旋转后,得到△P′AB
,求点P与点P′之间的距离,∠APB的度数.
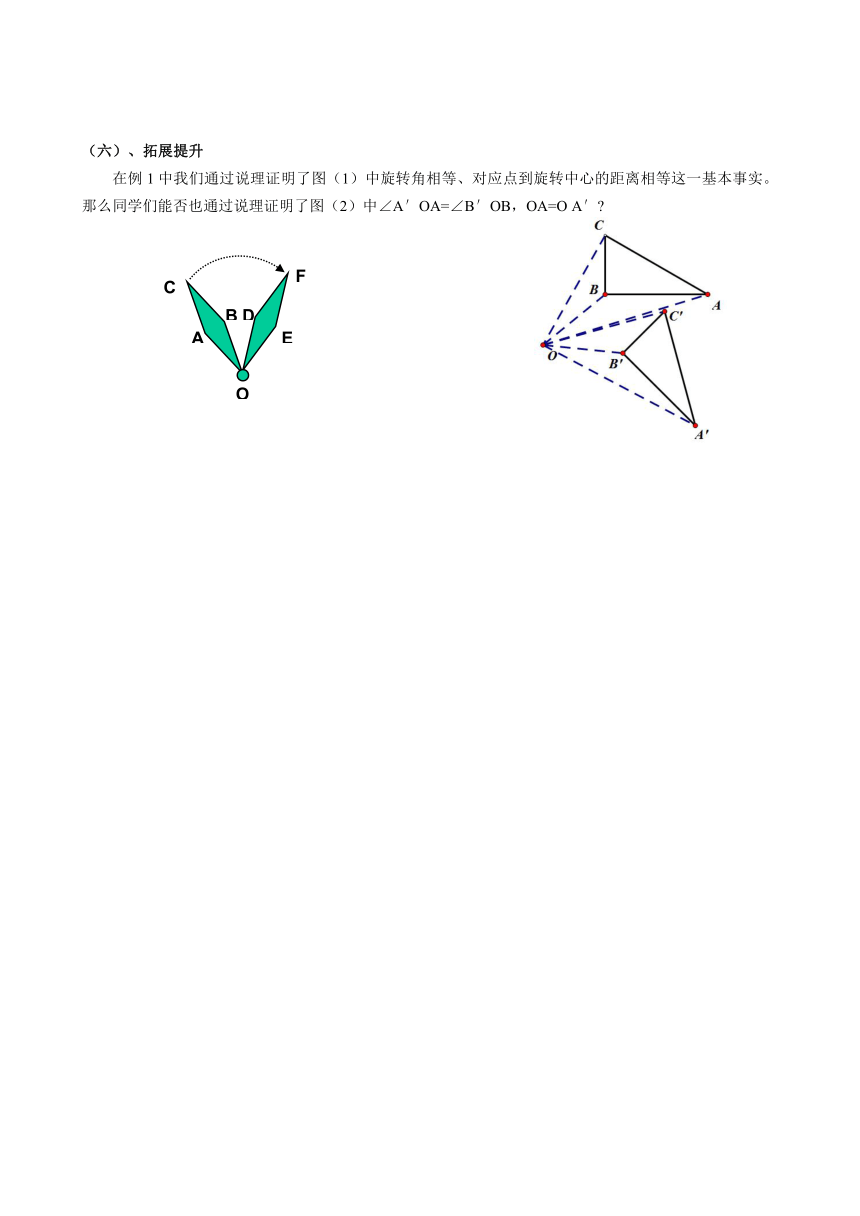
(六)、拓展提升
在例1中我们通过说理证明了图(1)
( http: / / www.21cnjy.com )中旋转角相等、对应点到旋转中心的距离相等这一基本事实。那么同学们能否也通过说理证明了图(2)中∠A′OA=∠B′OB,OA=O
A′
附:学生用学案
3.2图形的旋转
一、学习目标
1、通过类比平移及其相关的定义,能够确定旋转及其相关的定义。
2、通过类比平移的性质,能够探究出旋转的性质。
二、学习重难点:
重点:类比平移与旋转的异同,掌握旋转的定义和基本性质,并利用数学知识解释生活中的旋转现象.
难点:探索旋转的性质,特别是,对应点到旋转中心的距离相等
三、学习过程
(一)、知识回顾,构建动场
HYPERLINK
"http://www.21cnjy.com"
同学们,上图是我们已经学过的两种图形变换。你知道分别是哪两种么?
(二)、自主学习,把握概念
1、类比猜想:
( http: / / www.21cnjy.com )
结合大屏幕中的动图,谈一谈这几个例子有什么共同特征?将你的思考记录在下面。
2、总结结论:
(1)、旋转定义:
(2)、旋转的三要素:
、
、
。
根据上述定义,你能举出旋转的例子吗?并尝试指出你所举例的旋转三要素是?
3、尝试应用:
(1)、下列现象中是旋转的是 ( )
A.车轮在水平地面上滚动
B.火车车厢的直线运动
C.电梯的上下移动
D.汽车方向盘的转动
(2)、请你分别指出指出图中的旋转中心、旋转角。
(三)、动手操作,交流探究
1、问题引入:
请同学们利用手中的工具,将你喜欢的图形在硬纸
( http: / / www.21cnjy.com )板上做一次旋转,将旋转前后的图形在硬纸板上画出来。类比平移的性质探索旋转的性质,将你的结论记录下来:
2、实验报告:
通过实验,得出旋转的性质:
3、旋转性质的应用
例1、如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF.
在这个旋转过程中:
1.旋转中心是什么?旋转角是什么?
2.经过旋转,点A,B分别移动到什么位置?
3.AO与DO的长有什么关系?CO与FO呢?
4.
∠AOD与∠COF有什么大小关系
例2、△ABC是等边三角形,
△ABP顺时针旋转后能与△CBP’重合,那么:
(1)旋转中心是哪一点?
(2)旋转角是多少度?
(3)连结PP’后,△BPP’是什么三角形?
(四)、整体建构:
学生建构
教师建构
(五)、当堂检测
A组:
1、
同学们曾玩过万花筒,
( http: / / www.21cnjy.com )它是由三块等宽等长的玻璃片围成的.如图是看到的万花筒的一个图案,图中所有小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以A为中心(
).
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
2、钟表的分针经过40分钟,它转过的角度是(
)
A.120° B.240° C.150° D.180°
B组:
3、
把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,
若∠A′DC=89°,求∠A的度数
C组:
4、如图,P是正三角形
ABC
内的一点,且PA=6,PB=8,PC=10.若将△PAC
绕点A逆时针旋转后,得到△P′AB
,求点P与点P′之间的距离,∠APB的度数.
(六)、拓展提升
在例1中我们通过说理证明
( http: / / www.21cnjy.com )了图(1)中旋转角相等、对应点到旋转中心的距离相等这一基本事实。那么同学们能否也通过说理证明了图(2)中∠A′OA=∠B′OB,OA=O
A′
平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动成为平移.
平移的性质:
(1)、平移不改变
,只改变了
。
(2)、经过平移,对应点所连的线段
;对应线段
,对应角
。
O
A
B
D
E
C
F
C
A
B
P
O
A
B
D
E
C
F
平移的定义:在平面内,将一个图形
沿
移动
的距离,这样的图形运动成为平移.
平移的性质:
(1)、平移不改变
,只改变了
。
(2)、经过平移,对应点所连的线段
;对应线段
,对应角
。
O
A
B
D
E
C
F
C
A
B
P
O
A
B
D
E
C
F
图形的平移与旋转
第2节.图形的旋转(第1课时)
一、学生起点分析
学生在七年级下学期已经学习了“生活中的轴
( http: / / www.21cnjy.com )对称”一节,而且在本章的第一节,学生又经历了探索图形平移性质的过程,已经积累了相当的图形变换的数学活动经验,同时八年级学生逻辑思维从经验型逐步向理论型发展,观察能力、记忆能力和想象能力也在迅速发展,他们有强烈的独立思考、自主探索的愿望,这些对本节的学习都会有帮助。但旋转是三种变换中难度较大的一种,图形也比较复杂,因此,学生对旋转图形的形成过程的理解仍会有一定的困难。
二、教学任务分析
图形的旋转是继平移、轴对称之后的又一种图形基本变换,是义务教育阶段
数学课程标准中图形变换的一个重要组成部分。
( http: / / www.21cnjy.com )教材从学生实际接触、观察到的一些现象出发,从具体到抽象,从感性到理性,从实践到理论,再用理论检验实践,循序渐进地指导学生认识自然界和生活中的旋转,进而探索其性质。因此,旋转是培养学生思维能力、树立运动变化观点的良好素材;同时“图形的旋转”也为本章后续学习对称图形、中心对称图形做好准备,为今后学习“圆”的知识内容做好铺垫。
三、教学目标、重难点的确定
(一)教学目标
1、通过类比平移及其相关的定义,能够确定旋转及其相关的定义。
2、通过类比平移的性质,能够探究出旋转的性质。
(二)重难点
重点:类比平移与旋转的异同,掌握旋转的定义和基本性质,并利用数学知识解释生活中的旋转现象.
难点:探索旋转的性质,特别是,对应点到旋转中心的距离相等
四、学习过程
(一)、知识回顾,构建动场
HYPERLINK
"http://www.21cnjy.com"
同学们,上图是我们已经学过的两种图形变换。你知道分别是哪两种么?
师:同学们,在我们数学学习过程中有三大图形变换,前面我们已经学习了两种,请看屏幕。
这是?
(二)、自主学习,把握概念
师:很好,看来同学们对学过的内容掌握得非常的棒。
师:好,大家再来看这几个图,是不是我们学过的轴对称?是平移么?
既然他们既不是轴对称也不是平移,结合大屏幕中的动图,谈一谈这几个图有没有什么共同特征?将你的思考记录在学案上。
1、类比猜想:
( http: / / www.21cnjy.com )
结合大屏幕中的动图,谈一谈这几个例子有什么共同特征?将你的思考记录在学案上。
师:结合刚才同学们描述的三个方面,大家能不能描述一下点A是如何转动的呢?点B呢?线段oc呢?
我们把平面上能够具备这三方面转动的图形变换称为图形的旋转(板书)
这节课我们就一起来看一下图形的旋转
好,结合刚才的实例,大家把旋转的定义总结出来?找一个同学说一下。
好,刚才同学们总结出来的三个方面我们依据旋转的定义,分别称为……
大家回头再来看一下线段OC的旋转,如果老师在线段OC上取一点M,大家能描述一下点M是怎样运动的么?与线段OC的旋转是否相同?
2、总结结论:
(1)、旋转定义:
(2)、旋转的三要素:
、
、
。
师:根据上述定义,你能举出旋转的例子吗?
3、尝试应用:
(1)、下列现象中是旋转的是 ( )
A.车轮在水平地面上滚动
B.火车车厢的直线运动
C.电梯的上下移动
D.汽车方向盘的转动
(2)、请你分别指出指出图中的旋转中心、旋转角。
师:旋转角的定义:
师:研究了旋转的定义之后,数学兴趣小组的同学又给我们带来了一个的问题。请看视频.
(三)、动手操作,交流探究
1、问题引入:
请同学们利用手中的工具,将
( http: / / www.21cnjy.com )你喜欢的图形在硬纸板上做一次旋转,将旋转前后的图形在硬纸板上画出来。类比平移的性质探索旋转的性质,将你的结论记录下来:
2、实验报告:
通过实验,得出旋转的性质:
好,请同学上来展示一下你们小组的探究情况,并说一下你们小组的实验结论。
注意:此处多叫几个学生上黑板。
3、旋转性质的应用
例1、如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF.
在这个旋转过程中:
1.旋转中心是什么?旋转角是什么?
2.经过旋转,点A,B分别移动到什么位置?
3.AO与DO的长有什么关系?CO与FO呢?为什么(请简单说理)?
4.∠AOD与∠COF有什么大小关系?为什么(请简单说理)?
例2、△ABC是等边三角形,
△ABP顺时针旋转后能与△CBP’重合,那么:
(1)旋转中心是哪一点?
(2)旋转角是多少度?
(3)连结PP’后,△BPP’是什么三角形?
(四)、整体建构:
学生建构
教师建构
一种运动:图形的旋转,是一种运动;
两类思想:类比思想、转化思想;
三个要素:旋转中心,旋转方向,旋转角度;
四个性质:
①对应线段相等,对应角相等;
②对应点到旋转中心的距离相等;
③任意一对对应点与旋转中心的连线所成的角都等于旋转角;
④图形上的每一点都绕旋转中心沿相同方向转动了相同的角度.
(五)、当堂检测
A组:
1、
同学们曾玩过万花筒,它是由三块等
( http: / / www.21cnjy.com )宽等长的玻璃片围成的.如图是看到的万花筒的一个图案,图中所有小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以A为中心(
).
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
2、钟表的分针经过40分钟,它转过的角度是(
)
A.120° B.240° C.150° D.180°
B组:
3、
把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,
若∠A′DC=89°,求∠A的度数
C组:
4、如图,P是正三角形
ABC
内的一点,且PA=6,PB=8,PC=10.若将△PAC
绕点A逆时针旋转后,得到△P′AB
,求点P与点P′之间的距离,∠APB的度数.
(六)、拓展提升
在例1中我们通过说理证明了图(1)
( http: / / www.21cnjy.com )中旋转角相等、对应点到旋转中心的距离相等这一基本事实。那么同学们能否也通过说理证明了图(2)中∠A′OA=∠B′OB,OA=O
A′
附:学生用学案
3.2图形的旋转
一、学习目标
1、通过类比平移及其相关的定义,能够确定旋转及其相关的定义。
2、通过类比平移的性质,能够探究出旋转的性质。
二、学习重难点:
重点:类比平移与旋转的异同,掌握旋转的定义和基本性质,并利用数学知识解释生活中的旋转现象.
难点:探索旋转的性质,特别是,对应点到旋转中心的距离相等
三、学习过程
(一)、知识回顾,构建动场
HYPERLINK
"http://www.21cnjy.com"
同学们,上图是我们已经学过的两种图形变换。你知道分别是哪两种么?
(二)、自主学习,把握概念
1、类比猜想:
( http: / / www.21cnjy.com )
结合大屏幕中的动图,谈一谈这几个例子有什么共同特征?将你的思考记录在下面。
2、总结结论:
(1)、旋转定义:
(2)、旋转的三要素:
、
、
。
根据上述定义,你能举出旋转的例子吗?并尝试指出你所举例的旋转三要素是?
3、尝试应用:
(1)、下列现象中是旋转的是 ( )
A.车轮在水平地面上滚动
B.火车车厢的直线运动
C.电梯的上下移动
D.汽车方向盘的转动
(2)、请你分别指出指出图中的旋转中心、旋转角。
(三)、动手操作,交流探究
1、问题引入:
请同学们利用手中的工具,将你喜欢的图形在硬纸
( http: / / www.21cnjy.com )板上做一次旋转,将旋转前后的图形在硬纸板上画出来。类比平移的性质探索旋转的性质,将你的结论记录下来:
2、实验报告:
通过实验,得出旋转的性质:
3、旋转性质的应用
例1、如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF.
在这个旋转过程中:
1.旋转中心是什么?旋转角是什么?
2.经过旋转,点A,B分别移动到什么位置?
3.AO与DO的长有什么关系?CO与FO呢?
4.
∠AOD与∠COF有什么大小关系
例2、△ABC是等边三角形,
△ABP顺时针旋转后能与△CBP’重合,那么:
(1)旋转中心是哪一点?
(2)旋转角是多少度?
(3)连结PP’后,△BPP’是什么三角形?
(四)、整体建构:
学生建构
教师建构
(五)、当堂检测
A组:
1、
同学们曾玩过万花筒,
( http: / / www.21cnjy.com )它是由三块等宽等长的玻璃片围成的.如图是看到的万花筒的一个图案,图中所有小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以A为中心(
).
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
2、钟表的分针经过40分钟,它转过的角度是(
)
A.120° B.240° C.150° D.180°
B组:
3、
把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,
若∠A′DC=89°,求∠A的度数
C组:
4、如图,P是正三角形
ABC
内的一点,且PA=6,PB=8,PC=10.若将△PAC
绕点A逆时针旋转后,得到△P′AB
,求点P与点P′之间的距离,∠APB的度数.
(六)、拓展提升
在例1中我们通过说理证明
( http: / / www.21cnjy.com )了图(1)中旋转角相等、对应点到旋转中心的距离相等这一基本事实。那么同学们能否也通过说理证明了图(2)中∠A′OA=∠B′OB,OA=O
A′
平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动成为平移.
平移的性质:
(1)、平移不改变
,只改变了
。
(2)、经过平移,对应点所连的线段
;对应线段
,对应角
。
O
A
B
D
E
C
F
C
A
B
P
O
A
B
D
E
C
F
平移的定义:在平面内,将一个图形
沿
移动
的距离,这样的图形运动成为平移.
平移的性质:
(1)、平移不改变
,只改变了
。
(2)、经过平移,对应点所连的线段
;对应线段
,对应角
。
O
A
B
D
E
C
F
C
A
B
P
O
A
B
D
E
C
F
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
