北师大版六年级上册数学第二周 思维训练课 圆的周长与面积(二) 课件(共25张PPT)
文档属性
| 名称 | 北师大版六年级上册数学第二周 思维训练课 圆的周长与面积(二) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 08:05:20 | ||
图片预览





文档简介
(共25张PPT)
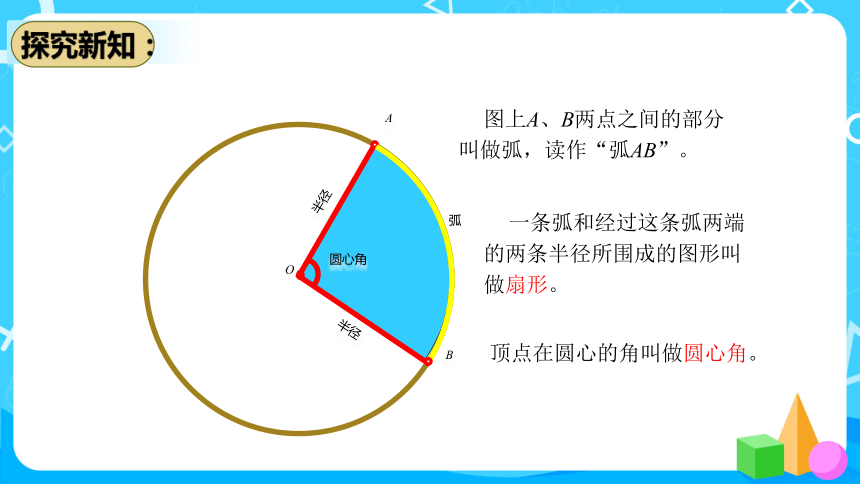
3.14×6÷2=9.42(cm)
6+2+2=10(cm)
3.14×10÷2=15.7(cm)
2+2=4(cm)
9.42+15.7+4=29.12(cm)
计算下图阴影部分的周长。
3.14×2×2=12.56(cm)
复习:
思维训练课
圆的周长与面积(二)
小学 / 数学 / 通用版 / 六年级上册
A
B
O
圆心角
半径
半径
弧
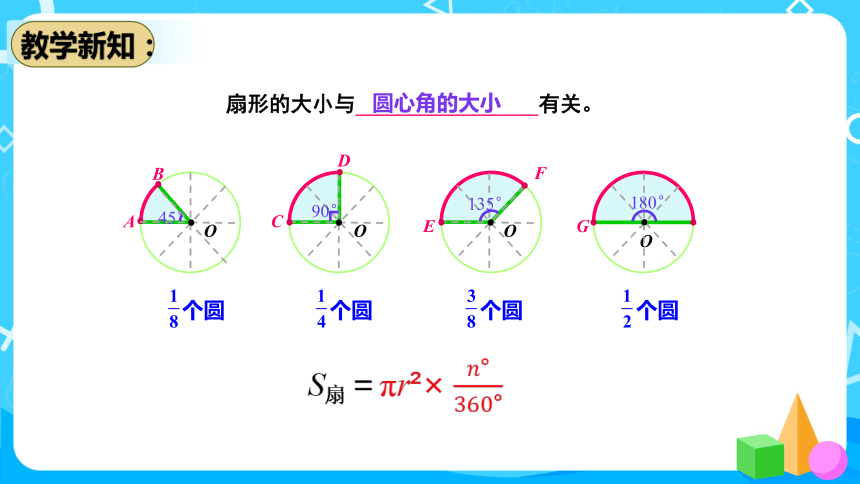
图上A、B两点之间的部分
叫做弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
探究新知:
比较下面扇形的大小,说一说是怎么比较的?
A
B
C
D
E
F
O
O
O
O
个圆
个圆
个圆
个圆
扇形的大小与_________________有关。
G
圆心角的大小
S扇=πr
45°
90°
135°
180°
教学新知:
思路点拨:这个图形的外形规则,空白部分规则,求阴影部分面积用“排空法”。用扇形面积减去三角形面积即可。
例题1:
求阴影部分的面积。(单位:厘米)
注意:图中的2厘米,既是扇形的半径。
又是三角形的底和高。
=
S扇=πr
=
S三=
=
=
3.14-2=
练一练:
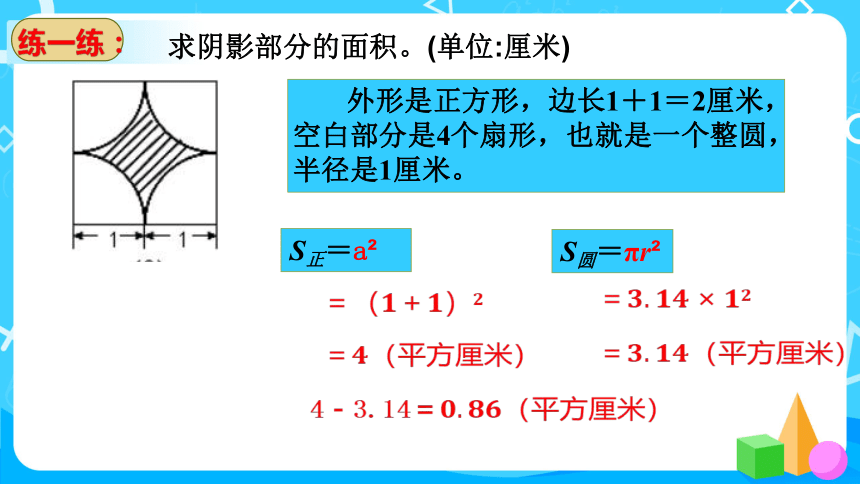
求阴影部分的面积。(单位:厘米)
外形是正方形,边长1+1=2厘米,空白部分是4个扇形,也就是一个整圆,半径是1厘米。
=
S正=a
=
S圆=πr
=
=
4-3.14=
例题2:
正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)
思路点拨:这个图形的外形规则,空白部分规则,求阴影部分面积用“排空法”。用正方形面积减扇形面积即可。可是扇形面积是难点,扇形的半径未知。要借助正方形面积解决扇形面积。
S正=7
S正=a
a =7
已知半径的平方,就可以直接计算扇形的面积了。
r =7
S扇=πr
n=90°
例题2:
正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)
S正=7
S正=a
a =7
=
7-5.495
S扇=πr
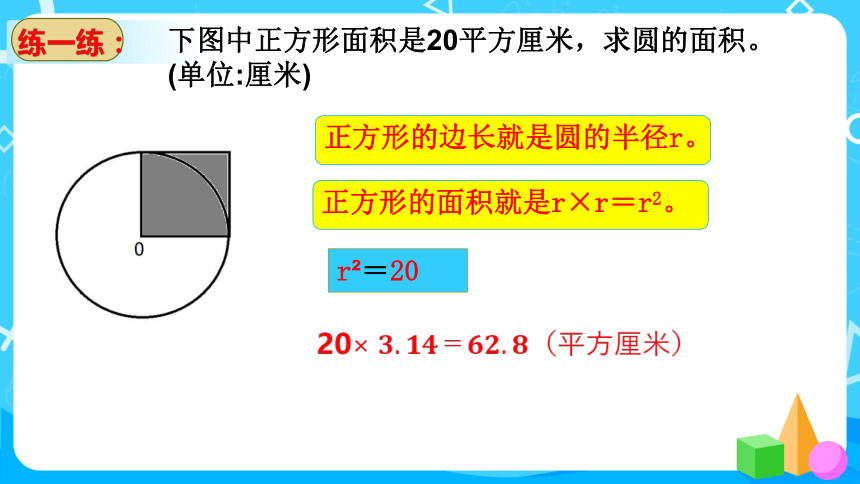
下图中正方形面积是20平方厘米,求圆的面积。
(单位:厘米)
r =20
正方形的边长就是圆的半径r。
正方形的面积就是r×r=r2。
20
练一练:
下图中的阴影部分的面积是20平方厘米,图中圆环的面积是多少?
阴影部分的是大正方形面积减去小正方形面积。
大正方形边长是圆环的大半径。
小正方形边长是圆环的小半径。
R2-r =20
S环=π(R2-r )
3.14×20=62.8(平方厘米)
练一练:
下图中,阴影部分的面积是25平方厘米,求圆环的面积。
假设大圆的半径为R厘米,小圆的半径为r厘米。
R -r =25×2=50
圆环的面积:
π(R -r )=3.14×50=157(cm )
阴影部分的面积=大三角形的面积-小三角形面积
R -r =25
练一练:
下图中,阴影部分的面积是25平方厘米,求圆环的面积。
假设大圆的半径为R厘米,小圆的半径为r厘米。
25×2=50(平方厘米)
3.14×50=157(cm )
阴影部分的面积=大三角形的面积-小三角形面积
练一练:
完整解答:
思路点拨:遇到这类不规则的图形,就想办法通过“旋转”、“平移”等方法将其变成规则图形,这道题就可以将右上角的图形顺时针旋转成一个扇形。
例题3:
求阴影部分的面积。(单位:厘米)
扇形的半径是2厘米。
πr
=×3.14×22
=3.14(平方厘米)
练一练:
求阴影部分的面积。(单位:厘米)
8×8÷2=32(平方厘米)
练一练:
求阴影部分的面积。(单位:厘米)
πr
= ×3.14×2
= ×3.14×4
= 6.28(平方厘米)
例题4:
求阴影部分的面积。(单位:厘米)
思路点拨:遇到这类不规则的图形,就想办法通过“旋转”、“平移”等方法将其变成规则图形,这道题就可以将左上角的一小块向右平移,使阴影部分成为规则图形。
(2+1)×2=6(平方厘米)
练一练:
求阴影部分的面积。(单位:厘米)
2×1=2(平方厘米)
思路点拨:用平移和旋转等方法无法解决,要分析阴影部分形成的过程,这是典型的容斥原理,俗称“扒皮法”。阴影部分的面积是由4个半圆面积的和减去1个正方形的面积得来的。
例题5:
求阴影部分的面积。(单位:厘米)
注意两个半圆重叠部分的形状。
思路点拨:用平移和旋转等方法无法解决,要分析阴影部分形成的过程,这是典型的容斥原理,俗称“扒皮法”。阴影部分的面积是由4个半圆面积的和减去1个正方形的面积得来的。
例题5:
求阴影部分的面积。(单位:厘米)
3.14×2×
= 3.14×8
= 25.12(平方厘米)
4×4 = 16(平方厘米)
25.12-16 = 9.12(平方厘米)
练一练:
求阴影部分的面积。(单位:厘米)
3.14×52×××
=(52)×3.14××
= 26.69(平方厘米)
5=15(平方厘米)
26.69-15=11.69(平方厘米)
求阴影部分的面积。(单位:厘米)
3.14×42×
=3.14×16×
25.12-16=9.12(平方厘米)
4×4=16(平方厘米)
=25.12(平方厘米)
练一练:
思路点拨:由于三个小扇形的圆心角度数未知,想将每个扇形的面积计算出来再相加是不可能完成的。要用“整体观察法”。由于三角形的内角和是180°,那么,将三个扇形拼在一起应该是一个半径3厘米的半圆。
例题6:
以任意三角形ABC的三个顶点为圆心画三个半径为6厘米的圆,求阴影部分的面积。
3.14×62×
=3.14×18
=56.52(平方厘米)
以A、B为圆心画两个半径为4厘米的圆,求阴影部分的面积。
3.14×42×
=3.14×16×
=12.56(平方厘米)
练一练:
练一练:
以梯形的四个顶点为圆心画4个半径相等的扇形,求阴影部分的面积。
思路点拨:四边形的内角和是360°,所以4个扇形的圆心角度数和是360°,从梯形的上底可以看出扇形的半径是2厘米,梯形的高正好是两个半径,是4厘米。
3.14×22=12.56(平方厘米)
(4+7)×4÷2=22(平方厘米)
22-12.56=9.44(平方厘米)
这节课有什么收获?
总结:
3.14×6÷2=9.42(cm)
6+2+2=10(cm)
3.14×10÷2=15.7(cm)
2+2=4(cm)
9.42+15.7+4=29.12(cm)
计算下图阴影部分的周长。
3.14×2×2=12.56(cm)
复习:
思维训练课
圆的周长与面积(二)
小学 / 数学 / 通用版 / 六年级上册
A
B
O
圆心角
半径
半径
弧
图上A、B两点之间的部分
叫做弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
探究新知:
比较下面扇形的大小,说一说是怎么比较的?
A
B
C
D
E
F
O
O
O
O
个圆
个圆
个圆
个圆
扇形的大小与_________________有关。
G
圆心角的大小
S扇=πr
45°
90°
135°
180°
教学新知:
思路点拨:这个图形的外形规则,空白部分规则,求阴影部分面积用“排空法”。用扇形面积减去三角形面积即可。
例题1:
求阴影部分的面积。(单位:厘米)
注意:图中的2厘米,既是扇形的半径。
又是三角形的底和高。
=
S扇=πr
=
S三=
=
=
3.14-2=
练一练:
求阴影部分的面积。(单位:厘米)
外形是正方形,边长1+1=2厘米,空白部分是4个扇形,也就是一个整圆,半径是1厘米。
=
S正=a
=
S圆=πr
=
=
4-3.14=
例题2:
正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)
思路点拨:这个图形的外形规则,空白部分规则,求阴影部分面积用“排空法”。用正方形面积减扇形面积即可。可是扇形面积是难点,扇形的半径未知。要借助正方形面积解决扇形面积。
S正=7
S正=a
a =7
已知半径的平方,就可以直接计算扇形的面积了。
r =7
S扇=πr
n=90°
例题2:
正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)
S正=7
S正=a
a =7
=
7-5.495
S扇=πr
下图中正方形面积是20平方厘米,求圆的面积。
(单位:厘米)
r =20
正方形的边长就是圆的半径r。
正方形的面积就是r×r=r2。
20
练一练:
下图中的阴影部分的面积是20平方厘米,图中圆环的面积是多少?
阴影部分的是大正方形面积减去小正方形面积。
大正方形边长是圆环的大半径。
小正方形边长是圆环的小半径。
R2-r =20
S环=π(R2-r )
3.14×20=62.8(平方厘米)
练一练:
下图中,阴影部分的面积是25平方厘米,求圆环的面积。
假设大圆的半径为R厘米,小圆的半径为r厘米。
R -r =25×2=50
圆环的面积:
π(R -r )=3.14×50=157(cm )
阴影部分的面积=大三角形的面积-小三角形面积
R -r =25
练一练:
下图中,阴影部分的面积是25平方厘米,求圆环的面积。
假设大圆的半径为R厘米,小圆的半径为r厘米。
25×2=50(平方厘米)
3.14×50=157(cm )
阴影部分的面积=大三角形的面积-小三角形面积
练一练:
完整解答:
思路点拨:遇到这类不规则的图形,就想办法通过“旋转”、“平移”等方法将其变成规则图形,这道题就可以将右上角的图形顺时针旋转成一个扇形。
例题3:
求阴影部分的面积。(单位:厘米)
扇形的半径是2厘米。
πr
=×3.14×22
=3.14(平方厘米)
练一练:
求阴影部分的面积。(单位:厘米)
8×8÷2=32(平方厘米)
练一练:
求阴影部分的面积。(单位:厘米)
πr
= ×3.14×2
= ×3.14×4
= 6.28(平方厘米)
例题4:
求阴影部分的面积。(单位:厘米)
思路点拨:遇到这类不规则的图形,就想办法通过“旋转”、“平移”等方法将其变成规则图形,这道题就可以将左上角的一小块向右平移,使阴影部分成为规则图形。
(2+1)×2=6(平方厘米)
练一练:
求阴影部分的面积。(单位:厘米)
2×1=2(平方厘米)
思路点拨:用平移和旋转等方法无法解决,要分析阴影部分形成的过程,这是典型的容斥原理,俗称“扒皮法”。阴影部分的面积是由4个半圆面积的和减去1个正方形的面积得来的。
例题5:
求阴影部分的面积。(单位:厘米)
注意两个半圆重叠部分的形状。
思路点拨:用平移和旋转等方法无法解决,要分析阴影部分形成的过程,这是典型的容斥原理,俗称“扒皮法”。阴影部分的面积是由4个半圆面积的和减去1个正方形的面积得来的。
例题5:
求阴影部分的面积。(单位:厘米)
3.14×2×
= 3.14×8
= 25.12(平方厘米)
4×4 = 16(平方厘米)
25.12-16 = 9.12(平方厘米)
练一练:
求阴影部分的面积。(单位:厘米)
3.14×52×××
=(52)×3.14××
= 26.69(平方厘米)
5=15(平方厘米)
26.69-15=11.69(平方厘米)
求阴影部分的面积。(单位:厘米)
3.14×42×
=3.14×16×
25.12-16=9.12(平方厘米)
4×4=16(平方厘米)
=25.12(平方厘米)
练一练:
思路点拨:由于三个小扇形的圆心角度数未知,想将每个扇形的面积计算出来再相加是不可能完成的。要用“整体观察法”。由于三角形的内角和是180°,那么,将三个扇形拼在一起应该是一个半径3厘米的半圆。
例题6:
以任意三角形ABC的三个顶点为圆心画三个半径为6厘米的圆,求阴影部分的面积。
3.14×62×
=3.14×18
=56.52(平方厘米)
以A、B为圆心画两个半径为4厘米的圆,求阴影部分的面积。
3.14×42×
=3.14×16×
=12.56(平方厘米)
练一练:
练一练:
以梯形的四个顶点为圆心画4个半径相等的扇形,求阴影部分的面积。
思路点拨:四边形的内角和是360°,所以4个扇形的圆心角度数和是360°,从梯形的上底可以看出扇形的半径是2厘米,梯形的高正好是两个半径,是4厘米。
3.14×22=12.56(平方厘米)
(4+7)×4÷2=22(平方厘米)
22-12.56=9.44(平方厘米)
这节课有什么收获?
总结:
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
