浙教版2024—2025学年八年级下册数学期末全真模拟试卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年八年级下册数学期末全真模拟试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 880.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年八年级下册数学期末全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.近年来,我国新能源品牌汽车新品纷呈.下列各新能源汽车图标中,不是中心对称图形的是( )
A. B. C. D.
2.用反证法证明命题结论“a<0”时,应先假设( )
A.a>0 B.a≥0 C.a=0 D.a≠0
3.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.体育课上,体育老师记录了40位同学的实心球成绩,数据分别为x1,x2,……x40.但由于场地布置失误,导致每位同学的成绩都少记录了10cm,其实际数据分别为y1,y2,……y40,比较记录成绩和实际成绩这两组数据,统计量不会发生变化的是( )
A.方差 B.中位数 C.众数 D.平均数
5.已知反比例函数,下列结论中不正确的是( )
A.图象必经过点(﹣3,2)
B.图象位于第二、四象限
C.x<0,则y>0
D.y随x的增大而增大
6.已知(x1,y1),B(x2,y2),C(x3,y3)是反比例函数的图象上的三个点,并且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y3<y1<y2
7.若关于x的一元二次方程4x2﹣4x+c=0有两个相等实数根,则c的值是( )
A.﹣1 B.1 C.﹣4 D.4
8.我们知道方程x2+2x﹣3=0的解是x1=1,x2=﹣3,现给出另一个方程(2x+3)2+2(2x+3)﹣3=0,它的解是( )
A.x1=1,x2=3 B.x1=1,x2=﹣3
C.x1=﹣1,x2=3 D.x1=﹣1,x2=﹣3
9.如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(不与A、B重合),作PE⊥AC于点E,PF⊥BC于点F,连接EF,则EF的最小值是( )
A.2.5 B.5
C.2.4 D.1.2
10.已知一元二次方程x2+ax+1=0,x2+bx+2=0,x2+cx+4=0,其中a,b,c是正实数,且满足b2=ac.设这三个方程不相等的实数根的个数分别为M1,M2,M3,则下列说法一定正确的是( )
A.若M1=2,M2=2,则M3=0 B.若M1=0,M2=2,则M3=0
C.若M1=1,M2=0,则M3=0 D.若M1=0,M2=0,则M3=0
二、填空题(每小题3分,满分18分)
11.甲、乙两人进行射击测试,每人10次射击平均成绩均为9环,方差分别为:S甲2=2平方环,S乙2=1.5平方环,则射击成绩较稳定的是 (填“甲”或“乙”)
12.若关于x的一元二次方程x2+kx﹣k﹣1=0有两个相等的实数根,则k的值为 .
13.计算一组数据的方差,列式为,则该组数据的方差是 .
14.在解方程x2+mx﹣n=0时,小王看错了m,解得方程的根为6与﹣1;小李看错了n,解得方程的根为2与﹣7,则原方程的解为 .
15.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
16.如图,在平行四边形ABCD中,AB=5,BC=8,将△BCD沿对角线BD折叠得到△BED,AD与BE交于点F.若F恰好为AD的中点,求BF= ;平行四边形ABCD的面积为 .
浙教版2024—2025学年八年级下册数学期末全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______ ______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
19.某校为了解初中学生每天的睡眠情况,随机调查了该校部分初中学生平均每天睡眠时间(单位:h).根据调查结果
请根据相关信息,解答下列问题:
(1)直接写出本次接受调查的学生人数和图1中m的值;
(2)求被调查的学生平均每天睡眠时间数据的平均数和中位数;
(3)全校共有1200名学生,请估算全校学生平均每天睡眠时间不低于8h的人数.
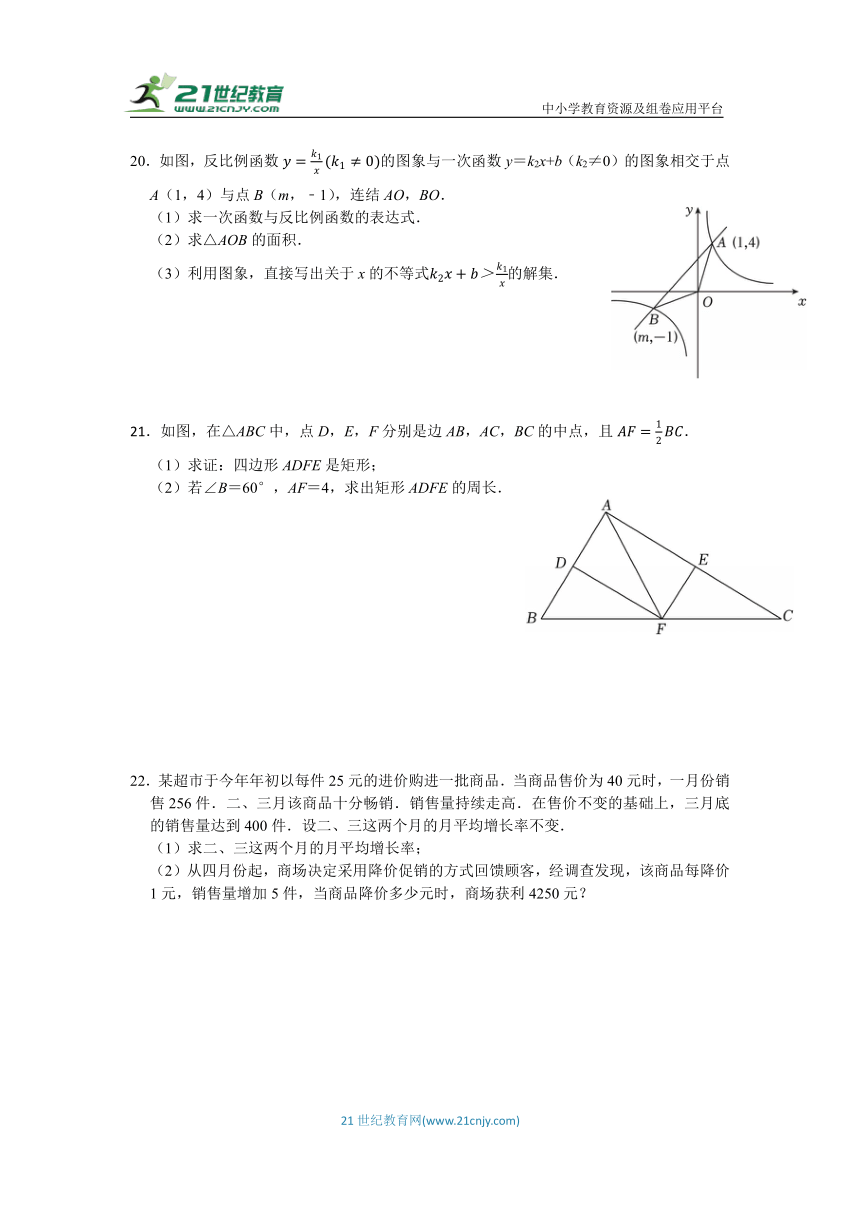
20.如图,反比例函数的图象与一次函数y=k2x+b(k2≠0)的图象相交于点A(1,4)与点B(m,﹣1),连结AO,BO.
(1)求一次函数与反比例函数的表达式.
(2)求△AOB的面积.
(3)利用图象,直接写出关于x的不等式的解集.
21.如图,在△ABC中,点D,E,F分别是边AB,AC,BC的中点,且.
(1)求证:四边形ADFE是矩形;
(2)若∠B=60°,AF=4,求出矩形ADFE的周长.
22.某超市于今年年初以每件25元的进价购进一批商品.当商品售价为40元时,一月份销售256件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到400件.设二、三这两个月的月平均增长率不变.
(1)求二、三这两个月的月平均增长率;
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?
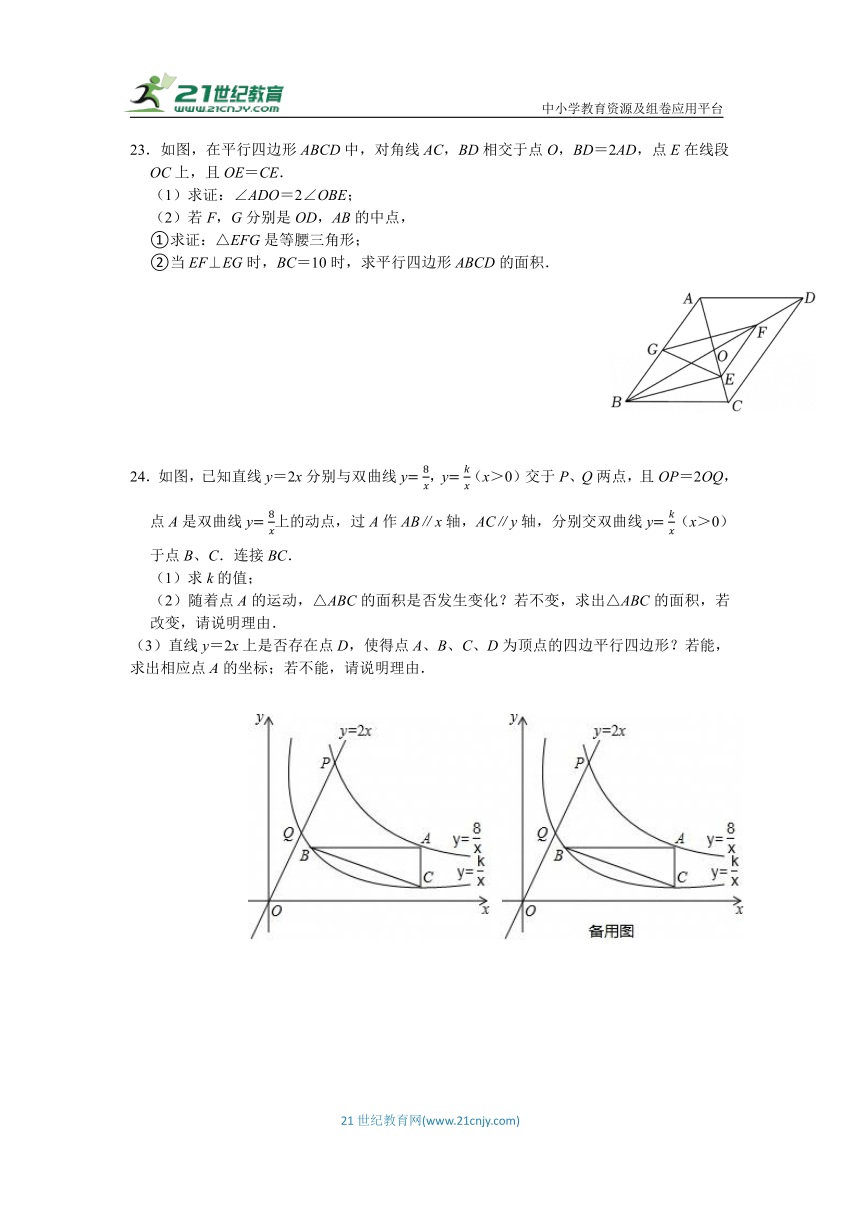
23.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.
(1)求证:∠ADO=2∠OBE;
(2)若F,G分别是OD,AB的中点,
①求证:△EFG是等腰三角形;
②当EF⊥EG时,BC=10时,求平行四边形ABCD的面积.
24.如图,已知直线y=2x分别与双曲线y,y(x>0)交于P、Q两点,且OP=2OQ,点A是双曲线y上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y(x>0)于点B、C.连接BC.
(1)求k的值;
(2)随着点A的运动,△ABC的面积是否发生变化?若不变,求出△ABC的面积,若改变,请说明理由.
(3)直线y=2x上是否存在点D,使得点A、B、C、D为顶点的四边平行四边形?若能,求出相应点A的坐标;若不能,请说明理由.
25.如图,在四边形ABCD中,∠A=∠C=90°,BE,DF分别平分∠ABC,∠ADC,BC于点E,F.ED=3,BE=11.4,CF=2BF=8,FD=10,G是DF的中点,点P在射线BE上.
(1)求证:BE∥DF.
(2)当以点B,G,P,D为顶点的四边形为平行四边形时,求PE的长.
(3)连结BG,GP,以BG,GP为邻边构造平行四边形BGPH,当GH与四边形ABCD的某一条边平行时,求出所有满足条件的GH的长.
参考答案
选择题
1—10:CBDAD DBDCC
二、填空题
11.【解答】解:∵S甲2=2>S乙2=1.5,方差小的为乙,
∴本题中成绩比较稳定的是乙.
故答案为:乙.
12.【解答】解:∵方程x2+kx﹣k﹣1=0有两个相等的实数根,
∴Δ=k2﹣4(﹣k﹣1)=k2+4k+4=(k+2)2=0,
解得:k=﹣2.
故答案为:﹣2.
13.【解答】解:由方差计算公式得这组数据为:2,4,7,5,7,
∴,
∴
=3.6;
故答案为:3.6.
14.【解答】解:根据根与系数关系得,
﹣n=6×(﹣1),﹣m=2﹣7,
解得:n=6,m=5,
∴原方程为x2+5x﹣6=0,
(x﹣1)(x+6)=0,
x﹣1=0或x+6=0,
∴x1=1,x2=﹣6,
故答案为:x1=1,x2=﹣6.
15.【解答】解:∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形的边数为6.
故答案为:6.
16.【解答】解:如图,过点B作BN⊥AD于N,过点F作FM⊥AB于M,
∵ABCD是平行四边形,
∴∠A=∠C,
∵∠E=∠C,
∴∠A=∠E,
∵F为AD的中点,
∴AF=DF,
在△AFB和△EFD中,
,
∴△AFB≌△EFD(AAS),
将△BCD沿对角线BD折叠得到△BED,
∴∠BDC=∠BDE=90°,
∴△BCD为直角三角形,
∵AB=5,BC=8,
∴CD=5,
在Rt△BCD中,,
∴平行四边形ABCD的面积为.
故答案为:.
17.【解答】解:(1)原式
=0;
(2)
.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
【解答】解:(1)50,40
5÷10%=50(人),
20÷50=40%,即m=40,
∴本次接受调查的学生人数为50人;图1中m的值为40;
(2)这组学生平均每天睡眠时间数据的平均数为:7×20%+8×40%+7×30%+7×10%=7.7;
将这50个数据从小到大排列后,处在中间位置的两个数都是6;
答:这组数据的平均数是7.7,中位数是2;
(3)1200×(40%+20%)=720(人),
答:全校学生平均每天睡眠时间不低于8h的人数约为720人
20.【解答】解:(1)∵A(1,4),
∴k1=4.
∴反比例函数表达式为.
把B(m,﹣1)代入反比例函数,得m=﹣4.
把A(1,4),B(﹣4,﹣1)代入y=k2x+b,
得,
∴,
∴一次函数表达式为y=x+3;
(2)如图,由(1)得C(0,3),又A(1,4),B(﹣4,﹣1),
∴;
(3)由图象可得:不等式的解集为﹣4<x<0或x>1.
21.【解答】(1)证明:连接DE.
∵E,F分别是边AC,BC的中点,
∴EF∥AB,EFAB,
∵点D是边AB的中点,
∴ADAB.
∴AD=EF.
∴四边形ADFE为平行四边形;
由点D,E分别是边AB,AC的中点,
∴DEBC.
∵AFBC,
∴DE=AF,
∴四边形ADFE为矩形;
(2)解:∵四边形ADFE为矩形,
∴∠BAC=∠FEC=90°,
∵AF=4,
∴BC=8,CF=4,
∵∠C=30°,
∴AC=4,∠B=60°,CE=2,EF=2,
∴AE=2,
∴矩形ADFE的周长=44.
21.【解答】解:(1)设二、三这两个月的月平均增长率为x,根据题意可得:
256(1+x)2=400,
解得:x1,x2(不合题意舍去).
答:二、三这两个月的月平均增长率为25%;
(2)设当商品降价m元时,商品获利4250元,根据题意可得:
(40﹣25﹣m)(400+5m)=4250,
解得:m1=5,m2=﹣70(不合题意舍去).
答:当商品降价5元时,商场获利4250元.
22.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,BD=2DO=2BO,
∴∠ADO=∠CBO,
∵BD=2AD,
∴AD=BO=BC,
∴△BOC是等腰三角形,
∵OE=CE,
∴∠OBE=∠CBE∠ADO,
∴∠ADO=2∠OBE.
(2)①证明:∵△BOC是等腰三角形,E是CO中点,
∴EB⊥CO,
∴∠BEA=90°,
∵G为AB中点,
∴EGAB,
∵E、F分别是OC、OD的中点,
∴EFCD,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴EG=EF,
∴△EFG是等腰三角形.
②解:由题意知,EF∥CD∥BG,
∴EFAB=BG,
∴四边形BEFG是平行四边形,
∴∠EFG=∠GBE,
∵∠FEG=∠AEB=90°,
∴△ABE是等腰三角形,
∴∠BAE=∠ABE=45°,
∴EG⊥AB,
设AG=GE=x,则BE=AEx,CE,
在Rt△BCE中,由勾股定理得,BC2=BE2+CE2,即,
解得x=3或x=﹣3(不合题意,舍去),
∴BE=3,AC=4CE=4,
∴S平行四边形ABCD=2120,
∴平行四边形ABCD的面积为120.
25.【解答】解:(1)过点Q作QE⊥x轴,垂足为E,过点P作PF⊥x轴,垂足为F,如图1,
联立,
解得:或.
∵x>0,
∴点P的坐标为(2,4).
∴OF=2,PF=4.
∵QE⊥x轴,PF⊥x轴,
∴QE∥PF.
∴△OEQ∽△OFP.
∴.
∵OP=2OQ,
∴OF=2OE=2,PF=2EQ=4.
∴OE=1,EQ=2.
∴点Q的坐标为(1,2).
∵点Q(1,2)在双曲线y上,
∴k=1×2=2.
∴k的值为2;
(2)如图2,
设点A的坐标为(a,b),
∵点A(a,b)在双曲线y上,
∴b.
∵.AB∥x轴,AC∥y轴,
∴xC=xA=a,yB=yA=b.
∵点B、C在双曲线y上,
∴xB,yC.
∴点B的坐标为(,),点C的坐标为(a,).
∴AB=aa,AC.
∴S△ABCAB AC
.
∴在点A运动过程中,△ABC的面积不变,始终等于.
(3)①AC为平行四边形的一边,
Ⅰ.当点B在点Q的右边时,如图3,
∵四边形ACBD是平行四边形,
∴AC∥BD,AC=BD.
∴xD=xB.
∴yD=2xD.
∴DB.
∵AC,
∴.
解得:a=±2.
经检验:a=±2是该方程的解.
∵a>0,
∴a=2.
∴b.
∴点A的坐标为(2,).
Ⅱ.当点B在点Q的左边且点C在点Q的右边时,如图4,
∵四边形ACDB是平行四边形,
∴AC∥BD,AC=BD.
∴xD=xB.
∴yD=2xD.
∴DB.
∵AC,
∴,
解得:a=±2.
经检验:a=±2是该方程的解.
∵a>0,
∴a=2.
∴b4.
∴点A的坐标为(2,4);
②AC为平行四边形的对角线,
此时点B、点C都在点Q的左边,如图5,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴yD=yC.
∴xD.
∴CDa.
∵AB=a,
∴a.
解得:a=±.
经检验:a=±是该方程的解.
∵a>0,
∴a.
∴b4.
∴点A的坐标为(,4).
综上所述:当点A、B、C、D为顶点的四边形为平行四边形时,此时点A的坐标为(2,)或(2,4)或(,4).
【解答】(1)证明:∵∠A+∠C+∠ABC+∠ADC=360°,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵BE,分别平分∠ABC,
∴∠CBE=,
∴∠CBE+∠ADF=90°,
∵∠C=90°,
∴∠ABC+∠AEB=90°,
∴∠AEB=∠ADF,
∴BE∥DF;
(2)解:如图1,
∵DG∥BP,点B,G,P,
∴BG∥DP,
∴PB=DG=DF=5,
∴PE=BE﹣PB=11.7﹣5=6.6;
(3)解:如图2,
当 GH∥AD时,设GH和PB交于点O,
∵BE∥DG,
∴四边形DEOC是平行四边形,
∴OG=DE=3,
∵四边形BGPH是平行四边形,
∴BG=3OG=6,
如图3,
当GH∥CD时,
∠DGO=∠CDF=∠ADF,
∵BE∥DF,
∴四边形DEOG是等腰梯形,
∴OG=DE=5,
∴GH=2OG=6,
如图4,
当GH∥AB时,
∠GOB=∠ABE=∠CBE,
∵BE∥DF,
∴四边形GOBF是等腰梯形,
∴OG=BF=4,
∴GH=2OG=6,
如图5,
当GH∥BC时,
∵BE∥DF,
∴四边形BGPH是平行四边形,
∴OG=BF=4,
∴GH=5OG=8,
综上所述:GH=6或5.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年八年级下册数学期末全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.近年来,我国新能源品牌汽车新品纷呈.下列各新能源汽车图标中,不是中心对称图形的是( )
A. B. C. D.
2.用反证法证明命题结论“a<0”时,应先假设( )
A.a>0 B.a≥0 C.a=0 D.a≠0
3.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.体育课上,体育老师记录了40位同学的实心球成绩,数据分别为x1,x2,……x40.但由于场地布置失误,导致每位同学的成绩都少记录了10cm,其实际数据分别为y1,y2,……y40,比较记录成绩和实际成绩这两组数据,统计量不会发生变化的是( )
A.方差 B.中位数 C.众数 D.平均数
5.已知反比例函数,下列结论中不正确的是( )
A.图象必经过点(﹣3,2)
B.图象位于第二、四象限
C.x<0,则y>0
D.y随x的增大而增大
6.已知(x1,y1),B(x2,y2),C(x3,y3)是反比例函数的图象上的三个点,并且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y3<y1<y2
7.若关于x的一元二次方程4x2﹣4x+c=0有两个相等实数根,则c的值是( )
A.﹣1 B.1 C.﹣4 D.4
8.我们知道方程x2+2x﹣3=0的解是x1=1,x2=﹣3,现给出另一个方程(2x+3)2+2(2x+3)﹣3=0,它的解是( )
A.x1=1,x2=3 B.x1=1,x2=﹣3
C.x1=﹣1,x2=3 D.x1=﹣1,x2=﹣3
9.如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(不与A、B重合),作PE⊥AC于点E,PF⊥BC于点F,连接EF,则EF的最小值是( )
A.2.5 B.5
C.2.4 D.1.2
10.已知一元二次方程x2+ax+1=0,x2+bx+2=0,x2+cx+4=0,其中a,b,c是正实数,且满足b2=ac.设这三个方程不相等的实数根的个数分别为M1,M2,M3,则下列说法一定正确的是( )
A.若M1=2,M2=2,则M3=0 B.若M1=0,M2=2,则M3=0
C.若M1=1,M2=0,则M3=0 D.若M1=0,M2=0,则M3=0
二、填空题(每小题3分,满分18分)
11.甲、乙两人进行射击测试,每人10次射击平均成绩均为9环,方差分别为:S甲2=2平方环,S乙2=1.5平方环,则射击成绩较稳定的是 (填“甲”或“乙”)
12.若关于x的一元二次方程x2+kx﹣k﹣1=0有两个相等的实数根,则k的值为 .
13.计算一组数据的方差,列式为,则该组数据的方差是 .
14.在解方程x2+mx﹣n=0时,小王看错了m,解得方程的根为6与﹣1;小李看错了n,解得方程的根为2与﹣7,则原方程的解为 .
15.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
16.如图,在平行四边形ABCD中,AB=5,BC=8,将△BCD沿对角线BD折叠得到△BED,AD与BE交于点F.若F恰好为AD的中点,求BF= ;平行四边形ABCD的面积为 .
浙教版2024—2025学年八年级下册数学期末全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______ ______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
19.某校为了解初中学生每天的睡眠情况,随机调查了该校部分初中学生平均每天睡眠时间(单位:h).根据调查结果
请根据相关信息,解答下列问题:
(1)直接写出本次接受调查的学生人数和图1中m的值;
(2)求被调查的学生平均每天睡眠时间数据的平均数和中位数;
(3)全校共有1200名学生,请估算全校学生平均每天睡眠时间不低于8h的人数.
20.如图,反比例函数的图象与一次函数y=k2x+b(k2≠0)的图象相交于点A(1,4)与点B(m,﹣1),连结AO,BO.
(1)求一次函数与反比例函数的表达式.
(2)求△AOB的面积.
(3)利用图象,直接写出关于x的不等式的解集.
21.如图,在△ABC中,点D,E,F分别是边AB,AC,BC的中点,且.
(1)求证:四边形ADFE是矩形;
(2)若∠B=60°,AF=4,求出矩形ADFE的周长.
22.某超市于今年年初以每件25元的进价购进一批商品.当商品售价为40元时,一月份销售256件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到400件.设二、三这两个月的月平均增长率不变.
(1)求二、三这两个月的月平均增长率;
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?
23.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.
(1)求证:∠ADO=2∠OBE;
(2)若F,G分别是OD,AB的中点,
①求证:△EFG是等腰三角形;
②当EF⊥EG时,BC=10时,求平行四边形ABCD的面积.
24.如图,已知直线y=2x分别与双曲线y,y(x>0)交于P、Q两点,且OP=2OQ,点A是双曲线y上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y(x>0)于点B、C.连接BC.
(1)求k的值;
(2)随着点A的运动,△ABC的面积是否发生变化?若不变,求出△ABC的面积,若改变,请说明理由.
(3)直线y=2x上是否存在点D,使得点A、B、C、D为顶点的四边平行四边形?若能,求出相应点A的坐标;若不能,请说明理由.
25.如图,在四边形ABCD中,∠A=∠C=90°,BE,DF分别平分∠ABC,∠ADC,BC于点E,F.ED=3,BE=11.4,CF=2BF=8,FD=10,G是DF的中点,点P在射线BE上.
(1)求证:BE∥DF.
(2)当以点B,G,P,D为顶点的四边形为平行四边形时,求PE的长.
(3)连结BG,GP,以BG,GP为邻边构造平行四边形BGPH,当GH与四边形ABCD的某一条边平行时,求出所有满足条件的GH的长.
参考答案
选择题
1—10:CBDAD DBDCC
二、填空题
11.【解答】解:∵S甲2=2>S乙2=1.5,方差小的为乙,
∴本题中成绩比较稳定的是乙.
故答案为:乙.
12.【解答】解:∵方程x2+kx﹣k﹣1=0有两个相等的实数根,
∴Δ=k2﹣4(﹣k﹣1)=k2+4k+4=(k+2)2=0,
解得:k=﹣2.
故答案为:﹣2.
13.【解答】解:由方差计算公式得这组数据为:2,4,7,5,7,
∴,
∴
=3.6;
故答案为:3.6.
14.【解答】解:根据根与系数关系得,
﹣n=6×(﹣1),﹣m=2﹣7,
解得:n=6,m=5,
∴原方程为x2+5x﹣6=0,
(x﹣1)(x+6)=0,
x﹣1=0或x+6=0,
∴x1=1,x2=﹣6,
故答案为:x1=1,x2=﹣6.
15.【解答】解:∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形的边数为6.
故答案为:6.
16.【解答】解:如图,过点B作BN⊥AD于N,过点F作FM⊥AB于M,
∵ABCD是平行四边形,
∴∠A=∠C,
∵∠E=∠C,
∴∠A=∠E,
∵F为AD的中点,
∴AF=DF,
在△AFB和△EFD中,
,
∴△AFB≌△EFD(AAS),
将△BCD沿对角线BD折叠得到△BED,
∴∠BDC=∠BDE=90°,
∴△BCD为直角三角形,
∵AB=5,BC=8,
∴CD=5,
在Rt△BCD中,,
∴平行四边形ABCD的面积为.
故答案为:.
17.【解答】解:(1)原式
=0;
(2)
.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
【解答】解:(1)50,40
5÷10%=50(人),
20÷50=40%,即m=40,
∴本次接受调查的学生人数为50人;图1中m的值为40;
(2)这组学生平均每天睡眠时间数据的平均数为:7×20%+8×40%+7×30%+7×10%=7.7;
将这50个数据从小到大排列后,处在中间位置的两个数都是6;
答:这组数据的平均数是7.7,中位数是2;
(3)1200×(40%+20%)=720(人),
答:全校学生平均每天睡眠时间不低于8h的人数约为720人
20.【解答】解:(1)∵A(1,4),
∴k1=4.
∴反比例函数表达式为.
把B(m,﹣1)代入反比例函数,得m=﹣4.
把A(1,4),B(﹣4,﹣1)代入y=k2x+b,
得,
∴,
∴一次函数表达式为y=x+3;
(2)如图,由(1)得C(0,3),又A(1,4),B(﹣4,﹣1),
∴;
(3)由图象可得:不等式的解集为﹣4<x<0或x>1.
21.【解答】(1)证明:连接DE.
∵E,F分别是边AC,BC的中点,
∴EF∥AB,EFAB,
∵点D是边AB的中点,
∴ADAB.
∴AD=EF.
∴四边形ADFE为平行四边形;
由点D,E分别是边AB,AC的中点,
∴DEBC.
∵AFBC,
∴DE=AF,
∴四边形ADFE为矩形;
(2)解:∵四边形ADFE为矩形,
∴∠BAC=∠FEC=90°,
∵AF=4,
∴BC=8,CF=4,
∵∠C=30°,
∴AC=4,∠B=60°,CE=2,EF=2,
∴AE=2,
∴矩形ADFE的周长=44.
21.【解答】解:(1)设二、三这两个月的月平均增长率为x,根据题意可得:
256(1+x)2=400,
解得:x1,x2(不合题意舍去).
答:二、三这两个月的月平均增长率为25%;
(2)设当商品降价m元时,商品获利4250元,根据题意可得:
(40﹣25﹣m)(400+5m)=4250,
解得:m1=5,m2=﹣70(不合题意舍去).
答:当商品降价5元时,商场获利4250元.
22.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,BD=2DO=2BO,
∴∠ADO=∠CBO,
∵BD=2AD,
∴AD=BO=BC,
∴△BOC是等腰三角形,
∵OE=CE,
∴∠OBE=∠CBE∠ADO,
∴∠ADO=2∠OBE.
(2)①证明:∵△BOC是等腰三角形,E是CO中点,
∴EB⊥CO,
∴∠BEA=90°,
∵G为AB中点,
∴EGAB,
∵E、F分别是OC、OD的中点,
∴EFCD,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴EG=EF,
∴△EFG是等腰三角形.
②解:由题意知,EF∥CD∥BG,
∴EFAB=BG,
∴四边形BEFG是平行四边形,
∴∠EFG=∠GBE,
∵∠FEG=∠AEB=90°,
∴△ABE是等腰三角形,
∴∠BAE=∠ABE=45°,
∴EG⊥AB,
设AG=GE=x,则BE=AEx,CE,
在Rt△BCE中,由勾股定理得,BC2=BE2+CE2,即,
解得x=3或x=﹣3(不合题意,舍去),
∴BE=3,AC=4CE=4,
∴S平行四边形ABCD=2120,
∴平行四边形ABCD的面积为120.
25.【解答】解:(1)过点Q作QE⊥x轴,垂足为E,过点P作PF⊥x轴,垂足为F,如图1,
联立,
解得:或.
∵x>0,
∴点P的坐标为(2,4).
∴OF=2,PF=4.
∵QE⊥x轴,PF⊥x轴,
∴QE∥PF.
∴△OEQ∽△OFP.
∴.
∵OP=2OQ,
∴OF=2OE=2,PF=2EQ=4.
∴OE=1,EQ=2.
∴点Q的坐标为(1,2).
∵点Q(1,2)在双曲线y上,
∴k=1×2=2.
∴k的值为2;
(2)如图2,
设点A的坐标为(a,b),
∵点A(a,b)在双曲线y上,
∴b.
∵.AB∥x轴,AC∥y轴,
∴xC=xA=a,yB=yA=b.
∵点B、C在双曲线y上,
∴xB,yC.
∴点B的坐标为(,),点C的坐标为(a,).
∴AB=aa,AC.
∴S△ABCAB AC
.
∴在点A运动过程中,△ABC的面积不变,始终等于.
(3)①AC为平行四边形的一边,
Ⅰ.当点B在点Q的右边时,如图3,
∵四边形ACBD是平行四边形,
∴AC∥BD,AC=BD.
∴xD=xB.
∴yD=2xD.
∴DB.
∵AC,
∴.
解得:a=±2.
经检验:a=±2是该方程的解.
∵a>0,
∴a=2.
∴b.
∴点A的坐标为(2,).
Ⅱ.当点B在点Q的左边且点C在点Q的右边时,如图4,
∵四边形ACDB是平行四边形,
∴AC∥BD,AC=BD.
∴xD=xB.
∴yD=2xD.
∴DB.
∵AC,
∴,
解得:a=±2.
经检验:a=±2是该方程的解.
∵a>0,
∴a=2.
∴b4.
∴点A的坐标为(2,4);
②AC为平行四边形的对角线,
此时点B、点C都在点Q的左边,如图5,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴yD=yC.
∴xD.
∴CDa.
∵AB=a,
∴a.
解得:a=±.
经检验:a=±是该方程的解.
∵a>0,
∴a.
∴b4.
∴点A的坐标为(,4).
综上所述:当点A、B、C、D为顶点的四边形为平行四边形时,此时点A的坐标为(2,)或(2,4)或(,4).
【解答】(1)证明:∵∠A+∠C+∠ABC+∠ADC=360°,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵BE,分别平分∠ABC,
∴∠CBE=,
∴∠CBE+∠ADF=90°,
∵∠C=90°,
∴∠ABC+∠AEB=90°,
∴∠AEB=∠ADF,
∴BE∥DF;
(2)解:如图1,
∵DG∥BP,点B,G,P,
∴BG∥DP,
∴PB=DG=DF=5,
∴PE=BE﹣PB=11.7﹣5=6.6;
(3)解:如图2,
当 GH∥AD时,设GH和PB交于点O,
∵BE∥DG,
∴四边形DEOC是平行四边形,
∴OG=DE=3,
∵四边形BGPH是平行四边形,
∴BG=3OG=6,
如图3,
当GH∥CD时,
∠DGO=∠CDF=∠ADF,
∵BE∥DF,
∴四边形DEOG是等腰梯形,
∴OG=DE=5,
∴GH=2OG=6,
如图4,
当GH∥AB时,
∠GOB=∠ABE=∠CBE,
∵BE∥DF,
∴四边形GOBF是等腰梯形,
∴OG=BF=4,
∴GH=2OG=6,
如图5,
当GH∥BC时,
∵BE∥DF,
∴四边形BGPH是平行四边形,
∴OG=BF=4,
∴GH=5OG=8,
综上所述:GH=6或5.
21世纪教育网(www.21cnjy.com)
同课章节目录
