浙教版2024—2025学年八年级下学期数学期末考试全真模拟试卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年八年级下学期数学期末考试全真模拟试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 531.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年八年级下学期数学期末考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,既是轴对称图形图形又是中心对称图形的是( )
A. B. C. D.
2.设数据0,1,2,3,4的平均数为a,中位数为b,方差c,则( )
A.a=b=c B.a=b<c C.a<b=c D.a<b<c
3.方程x2﹣x﹣1=0的根的情况是( )
A.没有实数根
B.两个不相等的实数根
C.两个相等的实数根
D.无法确定
4.用反证法证明“三角形中至少有一个内角大于或等于60°时,应假设( )
A.三角形的二个内角小于60°
B.三角形的三个内角都小于60°
C.三角形的二个内角大于60°
D.三角形的三个内角都大于60°
5.一元二次方程x2﹣4x=5配方后变形为( )
A.(x﹣4)2=5 B.(x﹣2)2=5
C.(x﹣4)2=9 D.(x﹣2)2=9
6.已知,则的值为( )
A. B. C.2025 D.4050
7.在下列条件中,能够判定 ABCD为菱形的是( )
A.AC=BD B.AC=AD C.AC⊥BD D.AB⊥BC
8.已知一元二次方程a(x﹣x1)(x﹣x2)=0(a≠0,x1≠x2)与一元一次方程dx+e=0有一个公共解x=x1,若一元二次方程a(x﹣x1)(x﹣x2)+(dx+e)=0有两个相等的实数根,则( )
A.a(x1﹣x2)=d B.a(x2﹣x1)=d
C.a(x1﹣x2)2=d D.a(x2﹣x1)2=d
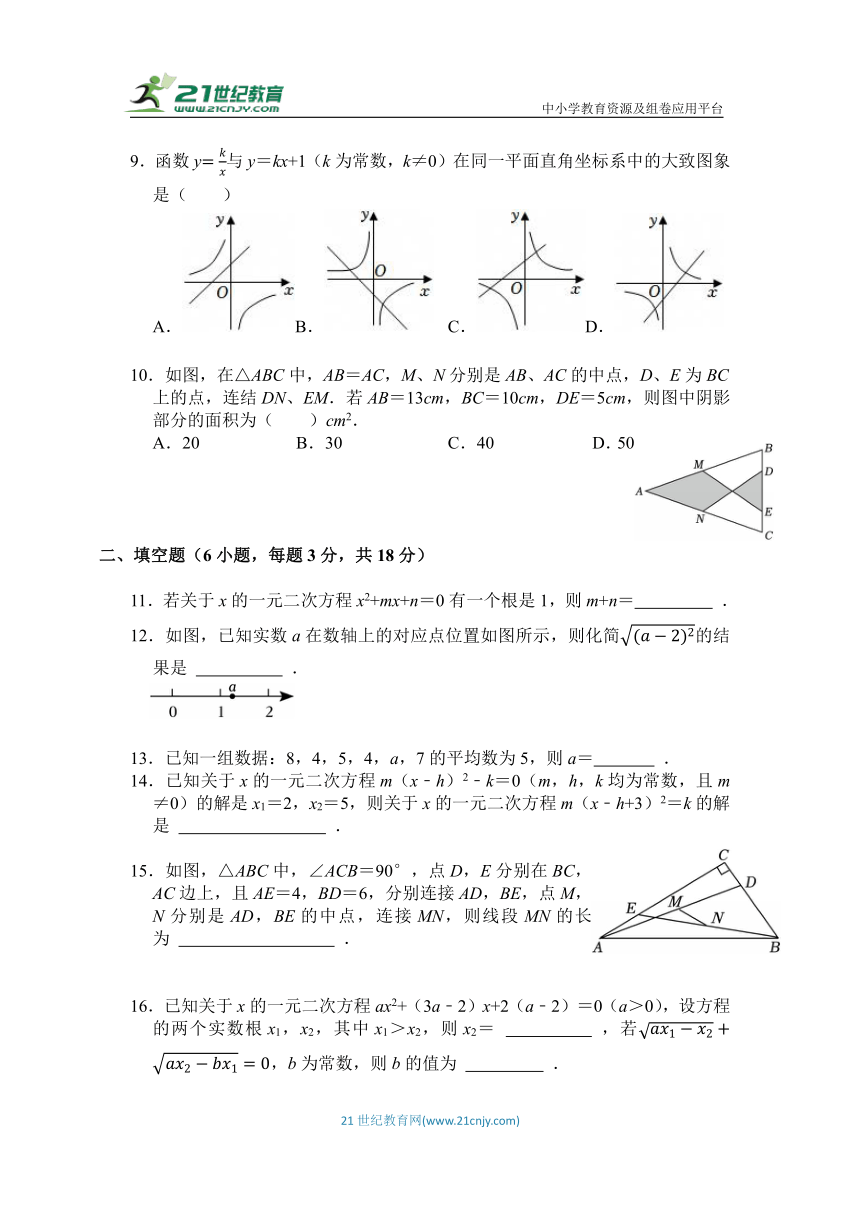
9.函数y与y=kx+1(k为常数,k≠0)在同一平面直角坐标系中的大致图象是( )
A.B. C.D.
10.如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为( )cm2.
A.20 B.30 C.40 D.50
二、填空题(6小题,每题3分,共18分)
11.若关于x的一元二次方程x2+mx+n=0有一个根是1,则m+n= .
12.如图,已知实数a在数轴上的对应点位置如图所示,则化简的结果是 .
13.已知一组数据:8,4,5,4,a,7的平均数为5,则a= .
14.已知关于x的一元二次方程m(x﹣h)2﹣k=0(m,h,k均为常数,且m≠0)的解是x1=2,x2=5,则关于x的一元二次方程m(x﹣h+3)2=k的解是 .
15.如图,△ABC中,∠ACB=90°,点D,E分别在BC,AC边上,且AE=4,BD=6,分别连接AD,BE,点M,N分别是AD,BE的中点,连接MN,则线段MN的长为 .
16.已知关于x的一元二次方程ax2+(3a﹣2)x+2(a﹣2)=0(a>0),设方程的两个实数根x1,x2,其中x1>x2,则x2= ,若,b为常数,则b的值为 .
浙教版2024—2025学年八年级下学期数学期末考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、_____、_____
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
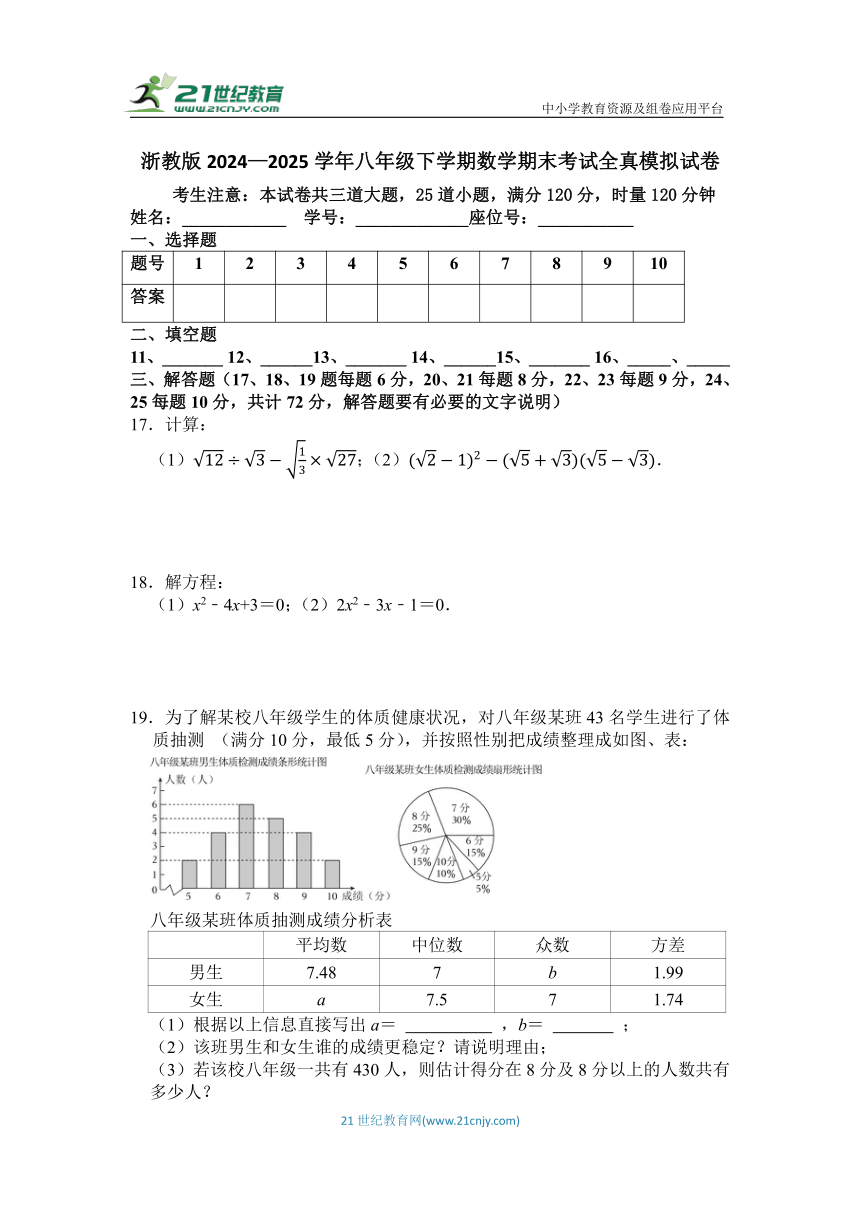
17.计算:
(1);(2).
18.解方程:
(1)x2﹣4x+3=0;(2)2x2﹣3x﹣1=0.
19.为了解某校八年级学生的体质健康状况,对八年级某班43名学生进行了体质抽测 (满分10分,最低5分),并按照性别把成绩整理成如图、表:
八年级某班体质抽测成绩分析表
平均数 中位数 众数 方差
男生 7.48 7 b 1.99
女生 a 7.5 7 1.74
(1)根据以上信息直接写出a= ,b= ;
(2)该班男生和女生谁的成绩更稳定?请说明理由;
(3)若该校八年级一共有430人,则估计得分在8分及8分以上的人数共有多少人?
20.位于宁波市江北区的保国寺以其精湛绝伦的建筑工艺闻名全国,其中大雄宝殿(又称无梁殿)更是以四绝“鸟不栖,蜘蛛不结网,梁上无灰尘”吸引了各地游客前来参观.据统计,第三天游客人数达到7200人次.
(1)求游客人数从假期第一天到第三天的平均日增长率;
(2)据悉,景区附近商店推出了保国寺旅游纪念章,每个纪念章的成本为5元,平均每天可售出500个,为了让游客尽可能得到优惠,售价每降低0.5元,平均每天可多售出100个,则售价应降低多少元?
21.设函数,函数y2=k2x+b(k1,k2,b是常数,k1≠0,k2≠0).若函数y1和函数y2的图象交于点A(2,m),B(3,2)
(1)求m的值.
(2)求函数y1,y2的表达式.
(3)请直接写出当y1>y2时,x的取值范围.
22.如图,在 ABCD中,AF平分∠BAD交BC于点F
(1)若AD=12,AB=8,求CF的长;
(2)连接BE和AF相交于点G,DF和CE相交于点H,求证:EF和GH互相平分.
23.已知关于x的方程x2﹣(k+4)x+2k+4=0.
(1)求证:该方程总有两个实数根;
(2)记该方程的两个实数根为x1,x2,求代数式(x1﹣2)(x2﹣2)的值;
(3)若,N=3﹣x1x2,比较M与N的大小.
24.阅读材料:
材料1:关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根x1,x2和系数a,b,c,有如下关系:,.
材料2:已知一元二次方程x2﹣x﹣1=0的两个实数根分别为m,n,求m2n+mn2的值.
解:∵m,n是一元二次方程x2﹣x﹣1=0的两个实数根,
∴m+n=1,mn=﹣1.
则m2n+mn2=mn(m+n)=﹣1×1=﹣1.
根据上述材料,结合你所学的知识,完成下列问题:
(1)应用:一元二次方程2x2+3x﹣1=0的两个实数根为x1,x2,则x1+x2= ,x1x2= ;
(2)类比:已知一元二次方程2x2+3x﹣1=0的两个实数根为m,n,求m2+n2的值;
(3)提升:已知实数s,t满足2s2+3s﹣1=0,2t2+3t﹣1=0且s≠t,求的值.
25.如图,在正方形ABCD中,点E,H,BC,CD边上,AH⊥EF于点M,且点M是AH的中点,GH,CG.
(1)求证:∠AEM=∠AHB;
(2)求证:AG⊥GH;
(3)若AG=GE,求AE:EB的值.
参考答案
一、选择题
1—10:BABBD BCBCB
二、填空题
11.【解答】解:把x=1代入原方程可得:
1+m+n=0,
∴m+n=﹣1,
故答案为:﹣1.
12.【解答】解:由实数a在数轴上的对应点位置可知1<a<2,
∴2﹣a.
故答案为:2﹣a.
13.【解答】解:∵一组数据:8,4,5,4,a,7的平均数为5,
∴,
解得a=2.
故答案为:2.
14.【解答】解:∵关于x的一元二次方程m(x﹣h)2﹣k=0(m,h,k均为常数,且m≠0)的解是x1=2,x2=5,即的解为x1=2,x2=5;
令x+3=y,
∴关于x的一元二次方程m(x﹣h+3)2=k化为m(y﹣h)2=k,
∵的解为x1=2,x2=5,
∴的解为y1=2,y2=5,即x+3=2或x+3=5,
∴x3=﹣1,x4=2,
∴关于x的一元二次方程m(x﹣h+3)2=k的解是x3=﹣1,x4=2,
故答案为:x3=﹣1,x4=2.
15.【解答】解:取AB的中点F,连接NF,MF,
∵∠CAB+∠CBA=90°,
∵点M是AD的中点,
∴MF是△ABD的中位线,
∴,MF∥BD,
∴∠AFM=∠CBA,
∵NF是△ABE的中位线,
∴,NF∥AE,
∴∠BFN=∠BAC,
∴∠BFN+∠AFM=∠BAC+∠CBA=90°,
∴∠MFN=90°,
∴MN2=MF2+NF2,
∴MN2=32+22=13,
∴.
故答案为:.
16.【解答】解:ax2+(3a﹣2)x+2(a﹣2)=0,
方程可变为:(ax+a﹣2)(x+2)=0,
∴ax+a﹣2=0或x+2=0,
解得:,x=﹣2,
∵a>0,
∴,
∵x1>x2,
∴,x2=﹣2;
∵,
∴,
∴,
∴,
解得:,
故答案为:﹣2;16.
三、解答题
17.【解答】解:(1)
=2﹣3
=﹣1;
(2)
=2﹣21﹣5+3
=1﹣2.
18.【解答】解:(1)x2﹣4x+3=0,
(x﹣3)(x﹣1)=0,
∴x﹣3=0或x﹣1=0,
∴x1=3,x2=1;
(2)2x2﹣3x﹣1=0,
∵a=2,b=﹣3,c=﹣1,
∴Δ=9﹣4×2×(﹣1)=17>0,
∴x,
∴x1,x2.
19.【解答】解:(1)由条形统计图可得,男生体质检测成绩7分的最多,
∴众数b=7,
由扇形统计图可得,a=8×5%+6×15%+4×30%+8×25%+9×15%+10×10%=7.6,
故答案为:7.6,7;
(2)女生的成绩更稳定,
理由:该班男生成绩的方差大于女生成绩的方差,所以该班女生的成绩更稳定;
(3)由条形统计图可得,八年级某班男生人数为2+2+6+5+8+2=23(人),
∴八年级某班女生人数为43﹣23=20(人),
∴八年级某班得分在8分及4分以上的人数为(5+4+2)+20×(25%+15%+10%)=21人,
∴430×=210(人),
答:该校八年级估计得分在8分及8分以上的人数共有210人.
20.【解答】解:(1)设游客人数从假期第一天到第三天的平均日增长率为x,
根据题意,得5000(1+x)2=7200,
解得x2=0.2,x6=﹣2.2(舍去).
答:平均增长率为20%;
(2)设售价应降低m元,
则每天的销量为(500+m)个.
根据题意可得(10﹣m﹣5)(500+m)=2800,
解得m1=,m2=7(舍去).
答:售价应降低元.
21.【解答】解:(1)由题意,∵B(31=上,
∴k1=3×6=6.
∴y1=.
又A(2,m)在函数y1=上,
∴2m=6.
∴m=3.
(2)由题意,根据(1)得,y1=,A(8,
又B(3,2),
∴.
∴.
∴y5=﹣x+5.
(3)由题意,在同一坐标系中画出y1=和y2=﹣x+5的图象如下,
∵当y4>y2时,x的取值范围即为反比例函数的图象在一次函数图象上方时对应的自变量的取值范围,
又A(2,6),2),
∴当y1>y6时,0<x<2或x>7.
22.【解答】(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=12,∠ABF=∠CDE,
∴∠DAF=∠AFB,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∴∠AFB=∠BAF,
∴BF=AB=8,
∴CF=BC﹣BF=12﹣8=7;
(2)证明:∵∠BAD=∠BCD,AF平分∠BAD,
∴∠BAF=∠DAF=∠FCE=∠DCE,
∵∠DAF=∠AFB,
∴∠FCE=∠AFB,
∴AF∥CE,
ABCD中,AE∥CF,
∴四边形AFCE是平行四边形,
∴AE=CF,
∴DE=BF,
∵AD∥BC,
∴四边形BFDE是平行四边形,
∴BE∥DF,
∵AF∥CE,
∴四边形EGFH是平行四边形,
∴EF和GH互相平分.
23.【解答】(1)证明:Δ=[﹣(k+4)]2﹣2(2k+4)
=k8+8k+16﹣8k﹣16
=k4,
∵k2≥0,
∴Δ≥7,
∴x2﹣(k+4)x+6k+4=0总有两个实数根;
(2)∵该方程的两个实数根为x2,x2,
∴x1+x5=k+4,x1 x3=2k+4,
∴(x7﹣2)(x2﹣8)
=x1 x2﹣4x1﹣2x7+4
=x1 x6﹣2(x1+x7)+4
=2k+6﹣2(k+4)+3
=2k+4﹣4k﹣8+4
=7;
(3)由(2)知,x1+x2=k+8,x1 x2=7k+4,
∵,N=4﹣x1x2,
∴M﹣N=+﹣3+x1x6
=(x1+x2)5﹣2x1x8﹣3+x1x2
=(x1+x2)2﹣x1x2﹣6
=(k+4)2﹣(6k+4)﹣3
=k3+16+8k﹣2k﹣2﹣3
=k2+3k+9
=(k+3)3≥0,
∴M≥N.
24.【解答】解:(1)∵一元二次方程2x2+3x﹣1=0的两个实数根为x1,x2,
∴x1+x2,x1 x2.
故答案为:,;
(2)∵一元二次方程 2x2+3x﹣1=0的两个实数根为m,n,
∴m+n,mn,
∴m2+n2=(m+n)2﹣2mn
=()2﹣2×()
1
;
(3)∵实数s,t满足2s2+3s﹣1=0,2t2+3t﹣1=0且s≠t,
∴s,t可以看作关于x的方程2x2+3x﹣1=0的两个根,
∴s+t,st,
∴(t﹣s)2=(t+s)2﹣4st=()2﹣4×(),
∴t﹣s=±,
∴±,
∴的值为或.
25.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠ABH=90°,
∵AH⊥EF于点M,
∴∠AME=90°,
∵∠AEM+∠AME+∠EAM=∠AHB+∠AHB+∠EAM=180°,
∴∠AEM=∠AHB.
(2)证明:连接BM,
∵四边形ABCD是正方形,
∴∠ABH=90°,∠ABD=∠CBD=45°,
∵点M是AH的中点,
∴BM=AM=MH,
∴∠1=∠2,
设∠4=∠2=x,
∴∠3=∠ABG﹣∠7=45°﹣x,∠AMB=180°﹣2x,
∵∠AME=90°,
∴∠4=90°﹣4x,
∴∠5=∠4﹣∠2=90°﹣2x﹣(45°﹣x)=45°﹣x,
∴∠5=∠4,
∴BM=MG=AM=MH,
∵∠AMG=∠HMG=90°,
∴∠MAG=∠MGA=∠MGH=∠MHG=45°,
∴∠AGH=90°,
∴AG⊥GH.
(3)解:∵AH⊥EF于点M,且点M是AH的中 点,
∴EF是AH的线段垂直平分线,
∴AG=GH,AE=EH,
∵AG=GE,
∴EG=GH,
∵AG=EG,
∴,
∴∠BEG=112.4°,
∴∠BGE=180°﹣45°﹣112.5°=22.5°,
∴∠BGE=∠BGH=22.3°,
∵BG=BG,EG=GH,
∴△GEB≌△GHB(SAS),
∴BE=BH,连接EH,
则△BEH是等腰直角三角形,BE2+BH2=EH8
∴
∴.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年八年级下学期数学期末考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,既是轴对称图形图形又是中心对称图形的是( )
A. B. C. D.
2.设数据0,1,2,3,4的平均数为a,中位数为b,方差c,则( )
A.a=b=c B.a=b<c C.a<b=c D.a<b<c
3.方程x2﹣x﹣1=0的根的情况是( )
A.没有实数根
B.两个不相等的实数根
C.两个相等的实数根
D.无法确定
4.用反证法证明“三角形中至少有一个内角大于或等于60°时,应假设( )
A.三角形的二个内角小于60°
B.三角形的三个内角都小于60°
C.三角形的二个内角大于60°
D.三角形的三个内角都大于60°
5.一元二次方程x2﹣4x=5配方后变形为( )
A.(x﹣4)2=5 B.(x﹣2)2=5
C.(x﹣4)2=9 D.(x﹣2)2=9
6.已知,则的值为( )
A. B. C.2025 D.4050
7.在下列条件中,能够判定 ABCD为菱形的是( )
A.AC=BD B.AC=AD C.AC⊥BD D.AB⊥BC
8.已知一元二次方程a(x﹣x1)(x﹣x2)=0(a≠0,x1≠x2)与一元一次方程dx+e=0有一个公共解x=x1,若一元二次方程a(x﹣x1)(x﹣x2)+(dx+e)=0有两个相等的实数根,则( )
A.a(x1﹣x2)=d B.a(x2﹣x1)=d
C.a(x1﹣x2)2=d D.a(x2﹣x1)2=d
9.函数y与y=kx+1(k为常数,k≠0)在同一平面直角坐标系中的大致图象是( )
A.B. C.D.
10.如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为( )cm2.
A.20 B.30 C.40 D.50
二、填空题(6小题,每题3分,共18分)
11.若关于x的一元二次方程x2+mx+n=0有一个根是1,则m+n= .
12.如图,已知实数a在数轴上的对应点位置如图所示,则化简的结果是 .
13.已知一组数据:8,4,5,4,a,7的平均数为5,则a= .
14.已知关于x的一元二次方程m(x﹣h)2﹣k=0(m,h,k均为常数,且m≠0)的解是x1=2,x2=5,则关于x的一元二次方程m(x﹣h+3)2=k的解是 .
15.如图,△ABC中,∠ACB=90°,点D,E分别在BC,AC边上,且AE=4,BD=6,分别连接AD,BE,点M,N分别是AD,BE的中点,连接MN,则线段MN的长为 .
16.已知关于x的一元二次方程ax2+(3a﹣2)x+2(a﹣2)=0(a>0),设方程的两个实数根x1,x2,其中x1>x2,则x2= ,若,b为常数,则b的值为 .
浙教版2024—2025学年八年级下学期数学期末考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、_____、_____
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1);(2).
18.解方程:
(1)x2﹣4x+3=0;(2)2x2﹣3x﹣1=0.
19.为了解某校八年级学生的体质健康状况,对八年级某班43名学生进行了体质抽测 (满分10分,最低5分),并按照性别把成绩整理成如图、表:
八年级某班体质抽测成绩分析表
平均数 中位数 众数 方差
男生 7.48 7 b 1.99
女生 a 7.5 7 1.74
(1)根据以上信息直接写出a= ,b= ;
(2)该班男生和女生谁的成绩更稳定?请说明理由;
(3)若该校八年级一共有430人,则估计得分在8分及8分以上的人数共有多少人?
20.位于宁波市江北区的保国寺以其精湛绝伦的建筑工艺闻名全国,其中大雄宝殿(又称无梁殿)更是以四绝“鸟不栖,蜘蛛不结网,梁上无灰尘”吸引了各地游客前来参观.据统计,第三天游客人数达到7200人次.
(1)求游客人数从假期第一天到第三天的平均日增长率;
(2)据悉,景区附近商店推出了保国寺旅游纪念章,每个纪念章的成本为5元,平均每天可售出500个,为了让游客尽可能得到优惠,售价每降低0.5元,平均每天可多售出100个,则售价应降低多少元?
21.设函数,函数y2=k2x+b(k1,k2,b是常数,k1≠0,k2≠0).若函数y1和函数y2的图象交于点A(2,m),B(3,2)
(1)求m的值.
(2)求函数y1,y2的表达式.
(3)请直接写出当y1>y2时,x的取值范围.
22.如图,在 ABCD中,AF平分∠BAD交BC于点F
(1)若AD=12,AB=8,求CF的长;
(2)连接BE和AF相交于点G,DF和CE相交于点H,求证:EF和GH互相平分.
23.已知关于x的方程x2﹣(k+4)x+2k+4=0.
(1)求证:该方程总有两个实数根;
(2)记该方程的两个实数根为x1,x2,求代数式(x1﹣2)(x2﹣2)的值;
(3)若,N=3﹣x1x2,比较M与N的大小.
24.阅读材料:
材料1:关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根x1,x2和系数a,b,c,有如下关系:,.
材料2:已知一元二次方程x2﹣x﹣1=0的两个实数根分别为m,n,求m2n+mn2的值.
解:∵m,n是一元二次方程x2﹣x﹣1=0的两个实数根,
∴m+n=1,mn=﹣1.
则m2n+mn2=mn(m+n)=﹣1×1=﹣1.
根据上述材料,结合你所学的知识,完成下列问题:
(1)应用:一元二次方程2x2+3x﹣1=0的两个实数根为x1,x2,则x1+x2= ,x1x2= ;
(2)类比:已知一元二次方程2x2+3x﹣1=0的两个实数根为m,n,求m2+n2的值;
(3)提升:已知实数s,t满足2s2+3s﹣1=0,2t2+3t﹣1=0且s≠t,求的值.
25.如图,在正方形ABCD中,点E,H,BC,CD边上,AH⊥EF于点M,且点M是AH的中点,GH,CG.
(1)求证:∠AEM=∠AHB;
(2)求证:AG⊥GH;
(3)若AG=GE,求AE:EB的值.
参考答案
一、选择题
1—10:BABBD BCBCB
二、填空题
11.【解答】解:把x=1代入原方程可得:
1+m+n=0,
∴m+n=﹣1,
故答案为:﹣1.
12.【解答】解:由实数a在数轴上的对应点位置可知1<a<2,
∴2﹣a.
故答案为:2﹣a.
13.【解答】解:∵一组数据:8,4,5,4,a,7的平均数为5,
∴,
解得a=2.
故答案为:2.
14.【解答】解:∵关于x的一元二次方程m(x﹣h)2﹣k=0(m,h,k均为常数,且m≠0)的解是x1=2,x2=5,即的解为x1=2,x2=5;
令x+3=y,
∴关于x的一元二次方程m(x﹣h+3)2=k化为m(y﹣h)2=k,
∵的解为x1=2,x2=5,
∴的解为y1=2,y2=5,即x+3=2或x+3=5,
∴x3=﹣1,x4=2,
∴关于x的一元二次方程m(x﹣h+3)2=k的解是x3=﹣1,x4=2,
故答案为:x3=﹣1,x4=2.
15.【解答】解:取AB的中点F,连接NF,MF,
∵∠CAB+∠CBA=90°,
∵点M是AD的中点,
∴MF是△ABD的中位线,
∴,MF∥BD,
∴∠AFM=∠CBA,
∵NF是△ABE的中位线,
∴,NF∥AE,
∴∠BFN=∠BAC,
∴∠BFN+∠AFM=∠BAC+∠CBA=90°,
∴∠MFN=90°,
∴MN2=MF2+NF2,
∴MN2=32+22=13,
∴.
故答案为:.
16.【解答】解:ax2+(3a﹣2)x+2(a﹣2)=0,
方程可变为:(ax+a﹣2)(x+2)=0,
∴ax+a﹣2=0或x+2=0,
解得:,x=﹣2,
∵a>0,
∴,
∵x1>x2,
∴,x2=﹣2;
∵,
∴,
∴,
∴,
解得:,
故答案为:﹣2;16.
三、解答题
17.【解答】解:(1)
=2﹣3
=﹣1;
(2)
=2﹣21﹣5+3
=1﹣2.
18.【解答】解:(1)x2﹣4x+3=0,
(x﹣3)(x﹣1)=0,
∴x﹣3=0或x﹣1=0,
∴x1=3,x2=1;
(2)2x2﹣3x﹣1=0,
∵a=2,b=﹣3,c=﹣1,
∴Δ=9﹣4×2×(﹣1)=17>0,
∴x,
∴x1,x2.
19.【解答】解:(1)由条形统计图可得,男生体质检测成绩7分的最多,
∴众数b=7,
由扇形统计图可得,a=8×5%+6×15%+4×30%+8×25%+9×15%+10×10%=7.6,
故答案为:7.6,7;
(2)女生的成绩更稳定,
理由:该班男生成绩的方差大于女生成绩的方差,所以该班女生的成绩更稳定;
(3)由条形统计图可得,八年级某班男生人数为2+2+6+5+8+2=23(人),
∴八年级某班女生人数为43﹣23=20(人),
∴八年级某班得分在8分及4分以上的人数为(5+4+2)+20×(25%+15%+10%)=21人,
∴430×=210(人),
答:该校八年级估计得分在8分及8分以上的人数共有210人.
20.【解答】解:(1)设游客人数从假期第一天到第三天的平均日增长率为x,
根据题意,得5000(1+x)2=7200,
解得x2=0.2,x6=﹣2.2(舍去).
答:平均增长率为20%;
(2)设售价应降低m元,
则每天的销量为(500+m)个.
根据题意可得(10﹣m﹣5)(500+m)=2800,
解得m1=,m2=7(舍去).
答:售价应降低元.
21.【解答】解:(1)由题意,∵B(31=上,
∴k1=3×6=6.
∴y1=.
又A(2,m)在函数y1=上,
∴2m=6.
∴m=3.
(2)由题意,根据(1)得,y1=,A(8,
又B(3,2),
∴.
∴.
∴y5=﹣x+5.
(3)由题意,在同一坐标系中画出y1=和y2=﹣x+5的图象如下,
∵当y4>y2时,x的取值范围即为反比例函数的图象在一次函数图象上方时对应的自变量的取值范围,
又A(2,6),2),
∴当y1>y6时,0<x<2或x>7.
22.【解答】(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=12,∠ABF=∠CDE,
∴∠DAF=∠AFB,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∴∠AFB=∠BAF,
∴BF=AB=8,
∴CF=BC﹣BF=12﹣8=7;
(2)证明:∵∠BAD=∠BCD,AF平分∠BAD,
∴∠BAF=∠DAF=∠FCE=∠DCE,
∵∠DAF=∠AFB,
∴∠FCE=∠AFB,
∴AF∥CE,
ABCD中,AE∥CF,
∴四边形AFCE是平行四边形,
∴AE=CF,
∴DE=BF,
∵AD∥BC,
∴四边形BFDE是平行四边形,
∴BE∥DF,
∵AF∥CE,
∴四边形EGFH是平行四边形,
∴EF和GH互相平分.
23.【解答】(1)证明:Δ=[﹣(k+4)]2﹣2(2k+4)
=k8+8k+16﹣8k﹣16
=k4,
∵k2≥0,
∴Δ≥7,
∴x2﹣(k+4)x+6k+4=0总有两个实数根;
(2)∵该方程的两个实数根为x2,x2,
∴x1+x5=k+4,x1 x3=2k+4,
∴(x7﹣2)(x2﹣8)
=x1 x2﹣4x1﹣2x7+4
=x1 x6﹣2(x1+x7)+4
=2k+6﹣2(k+4)+3
=2k+4﹣4k﹣8+4
=7;
(3)由(2)知,x1+x2=k+8,x1 x2=7k+4,
∵,N=4﹣x1x2,
∴M﹣N=+﹣3+x1x6
=(x1+x2)5﹣2x1x8﹣3+x1x2
=(x1+x2)2﹣x1x2﹣6
=(k+4)2﹣(6k+4)﹣3
=k3+16+8k﹣2k﹣2﹣3
=k2+3k+9
=(k+3)3≥0,
∴M≥N.
24.【解答】解:(1)∵一元二次方程2x2+3x﹣1=0的两个实数根为x1,x2,
∴x1+x2,x1 x2.
故答案为:,;
(2)∵一元二次方程 2x2+3x﹣1=0的两个实数根为m,n,
∴m+n,mn,
∴m2+n2=(m+n)2﹣2mn
=()2﹣2×()
1
;
(3)∵实数s,t满足2s2+3s﹣1=0,2t2+3t﹣1=0且s≠t,
∴s,t可以看作关于x的方程2x2+3x﹣1=0的两个根,
∴s+t,st,
∴(t﹣s)2=(t+s)2﹣4st=()2﹣4×(),
∴t﹣s=±,
∴±,
∴的值为或.
25.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠ABH=90°,
∵AH⊥EF于点M,
∴∠AME=90°,
∵∠AEM+∠AME+∠EAM=∠AHB+∠AHB+∠EAM=180°,
∴∠AEM=∠AHB.
(2)证明:连接BM,
∵四边形ABCD是正方形,
∴∠ABH=90°,∠ABD=∠CBD=45°,
∵点M是AH的中点,
∴BM=AM=MH,
∴∠1=∠2,
设∠4=∠2=x,
∴∠3=∠ABG﹣∠7=45°﹣x,∠AMB=180°﹣2x,
∵∠AME=90°,
∴∠4=90°﹣4x,
∴∠5=∠4﹣∠2=90°﹣2x﹣(45°﹣x)=45°﹣x,
∴∠5=∠4,
∴BM=MG=AM=MH,
∵∠AMG=∠HMG=90°,
∴∠MAG=∠MGA=∠MGH=∠MHG=45°,
∴∠AGH=90°,
∴AG⊥GH.
(3)解:∵AH⊥EF于点M,且点M是AH的中 点,
∴EF是AH的线段垂直平分线,
∴AG=GH,AE=EH,
∵AG=GE,
∴EG=GH,
∵AG=EG,
∴,
∴∠BEG=112.4°,
∴∠BGE=180°﹣45°﹣112.5°=22.5°,
∴∠BGE=∠BGH=22.3°,
∵BG=BG,EG=GH,
∴△GEB≌△GHB(SAS),
∴BE=BH,连接EH,
则△BEH是等腰直角三角形,BE2+BH2=EH8
∴
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
