北师大版六年级上册数学第一周思维训练课圆的周长与面积(一) 课件(共20张PPT)
文档属性
| 名称 | 北师大版六年级上册数学第一周思维训练课圆的周长与面积(一) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 09:18:23 | ||
图片预览








文档简介
(共20张PPT)
计算下面各圆的周长(先写出计算公式再脱式计算)。
=2×3.14×5
=31.4(cm)
=3.14×8
=25.12(cm)
=2×3.14×6
=37.68(cm)
C =πd
C=2πr
C=2πr
复习:
半圆形花圃的半径是5米,要在花圃周围围篱笆,需要多长的篱笆?(π取近似数3.14)
C半= πr +2r
=3.14×5 +2×5
=15.7 +10
=25.7(米)
C半= 5.14r
=5.14 ×5
=25.7(米)
答:需要25.7米长篱笆。
复习:
填空。
(1)圆的周长是指围成圆的( )的长度。
(2)车轮的直径越大,滚动一圈就行走路程的越( )。
(3)一个圆环形的机器零件,在10 cm长的标尺上正好能
滚动5圈,这个圆环形机器零件的周长是( )。
(4)在正方形内画一个最大的圆(如下图),半径为r,正方
形的周长是( )。
(5)圆的周长除以直径的商是一个固定的数,我们把它
叫作( ),用字母( )表示,它是一个
无限不循环小数,在小学阶段我们计算时通常取其
值为( )。
曲线
远
2 cm
8r
圆周率
π
3.14
复习:
思维训练课
圆的周长与面积(一)
小学 / 数学 / 北师大版 / 六年级上册
求下面图形中涂色部分的周长。
大圆弧长度:
2×3.14×4÷2=12.56(cm)
小圆弧长度:
2×3.14×3÷2=9.42(cm)
右侧线段长度:
3-(4-3)=2(cm)
左侧线段长度:
4 cm
12.56+9.42+2+4=27.98(cm)
阴影部分周长:
思路点拨:分析与圆相关的图形周长时,要注意观察图形周长中包含几条圆弧,几条线段。图中阴影部分周长包括大小两个圆周长的一半,一条大圆的半径和右侧的一条线段(线段长度与两个圆的半径有关)。
例题1:
求下面图形中涂色部分的周长。
大圆弧长度:
2×3.14×2÷2=6.28(cm)
小圆弧长度:
2×3.14÷2=3.14(cm)
大圆半径:
2 cm
阴影部分的周长:
6.28+3.14+2=11.42(cm)
练一练:
思路点拨:已知小圆的直径,可以分别算出红蚂蚁和黑蚂蚁爬行的路程,通过比较就可以知道谁爬的路程多了。
例题2:
两只小蚂蚁在下图中寻找食物。红蚂蚁从A点出发,沿着大圆爬了一圈回到A点。黑蚂蚁也从A点出发,沿着内部的8字形爬了一圈回到A点。如果每个小圆的直径都是10米,算一算,谁爬的路程多?
红蚂蚁:
黑蚂蚁:
2×3.14×10=62.8(m)
3.14×10+3.14×10=62.8(m)
62.8=62.8
答:两只蚂蚁爬的路程相等。
例题2:
(2)如果黑蚂蚁的行走路线如下图所示,小圆直径8米,中圆直径12米,那么请问谁爬的路程多?
两只小蚂蚁在下图中寻找食物。红蚂蚁从A点出发,沿着大圆爬了一圈回到A点。黑蚂蚁也从A点出发,沿着内部的8字形爬了一圈回到A点。
红蚂蚁:
3.14×(8+12)=62.8(m)
黑蚂蚁:
3.14×8+3.14×12=62.8(m)
62.8=62.8
答:两只蚂蚁爬的路程相等。
例题2:
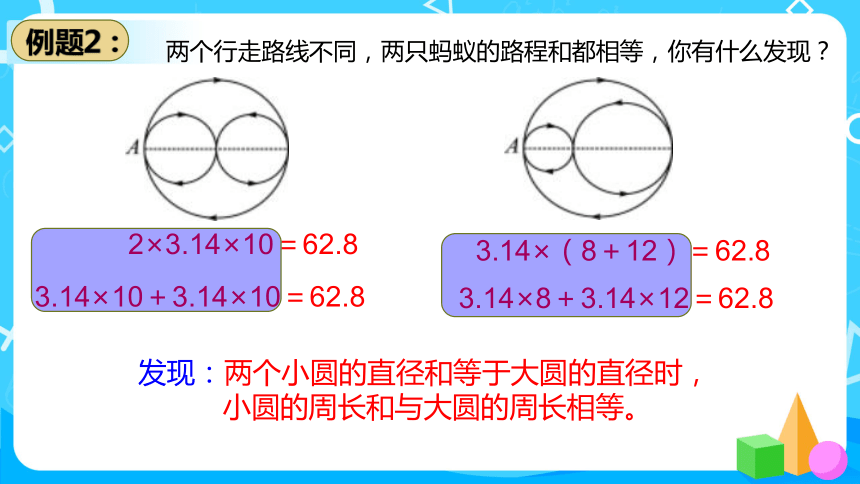
两个行走路线不同,两只蚂蚁的路程和都相等,你有什么发现?
2×3.14×10=62.8
3.14×10+3.14×10=62.8
发现:两个小圆的直径和等于大圆的直径时,
小圆的周长和与大圆的周长相等。
3.14×(8+12)=62.8
3.14×8+3.14×12=62.8
如果大圆中的小圆数量增加,这个结论仍然成立。
例题2:
如果都变成半圆呢?
1、计算下面图形阴影部分的周长。(单位:cm)
3.14×(3+5)=25.12(cm)
练一练:
8cm
2、计算下面图形的周长。(单位:cm)
3.14×8×2=50.24(cm)
练一练:
求下面图形中涂色部分的周长。
3.14×2×2=12.56(cm)
思路点拨:彩绳长度包括4段圆弧和4条线段的长度。每段圆弧都是以4厘米为直径圆的四分之一,合在一起正好是一个整圆周长,4条线段正好是4条直径的长度。
例题3:
把四个圆柱形的薯片筒用彩绳捆在一起(底面如下图),捆一圈至少用彩绳多少厘米?(接头处忽略不计)
4条圆弧长度和:
3.14×4=12.56(cm)
4条线段长度和:
4×4=16(cm)
彩绳长度:
12.56+16=28.56(cm)
答:捆一圈至少用彩绳28.56厘米。
超市促销一种饮料,促销包装如下图。已知每个饮料瓶的外直径都是8厘米,每个促销包装上下各捆1圈绳子,打结处都需要10厘米的绳子。要包装一个这样的促销包装至少需要多长的绳子?
练一练:
4条圆弧长度和:
3.14×8=25.12(cm)
4条线段长度和:
打结处长度:
8×6=48(cm)
10 cm
(25,12+48+10)×2
=83.12×2
=166.24(cm)
绳子总长度:
答:包装一个这样的促销包装至少需要166.24厘米的绳子。
思路点拨:跑一圈多少米就是求这个图形的周长,周长中包括两条直道的长度(2条线段),还有2条圆弧的长度(2条圆弧合起来是整圆的周长)。分别计算出来再相加即可。
例题4:
下图是学校操场的示意图(单位:米),绕着操场跑一圈至少要跑多少米?
2条直道长度和:
2条圆弧长度和:
跑道周长:
100×2=200(m)
3.14×60=188.4(m)
200+188.4=388.4(m)
答:至少要跑388.4米。
下图是一个运动场的跑道,围绕这个跑道跑一圈是400米,已知跑道两边的直道长130米,求跑道半圆部分的直径是多少米?(π取近似数3;结果保留一位小数)
练一练:
400-130×2=140(m)
140÷3≈46.7(m)
答:跑道半圆部分的直径约是46.7米。
下图中每个小圆的半径都是1cm,求阴影部分的周长。
例题5:
思路点拨:图中阴影部分的周长看似很复杂,仔细观察会发现,阴影部分的周长就是所有小圆的周长加上1个大圆的周长。通过已知条件“小圆的半径是1厘米”可知大圆的直径是1×2×3=6厘米。
小圆的周长和:
2×3.14×1×7=43.96(cm)
大圆的周长:
1×2×3=6(cm)
3.14×6=18.84(cm)
阴影部分的周长:
43.96+18.84=62.8(cm)
练一练:
下图中虚线正方形的边长是4cm,求阴影部分的周长。
4条圆弧长度和:
4条线段长度和:
阴影部分周长:
2×3.14×4=25.12(cm)
4×4=16(cm)
25.12+16=41.12(cm)
3.14×6÷2=9.42(cm)
6+2+2=10(cm)
3.14×10÷2=15.7(cm)
2+2=4(cm)
9.42+15.7+4=29.12(cm)
练一练:
计算下图阴影部分的周长。
课堂总结:
这节课有什么收获?
计算下面各圆的周长(先写出计算公式再脱式计算)。
=2×3.14×5
=31.4(cm)
=3.14×8
=25.12(cm)
=2×3.14×6
=37.68(cm)
C =πd
C=2πr
C=2πr
复习:
半圆形花圃的半径是5米,要在花圃周围围篱笆,需要多长的篱笆?(π取近似数3.14)
C半= πr +2r
=3.14×5 +2×5
=15.7 +10
=25.7(米)
C半= 5.14r
=5.14 ×5
=25.7(米)
答:需要25.7米长篱笆。
复习:
填空。
(1)圆的周长是指围成圆的( )的长度。
(2)车轮的直径越大,滚动一圈就行走路程的越( )。
(3)一个圆环形的机器零件,在10 cm长的标尺上正好能
滚动5圈,这个圆环形机器零件的周长是( )。
(4)在正方形内画一个最大的圆(如下图),半径为r,正方
形的周长是( )。
(5)圆的周长除以直径的商是一个固定的数,我们把它
叫作( ),用字母( )表示,它是一个
无限不循环小数,在小学阶段我们计算时通常取其
值为( )。
曲线
远
2 cm
8r
圆周率
π
3.14
复习:
思维训练课
圆的周长与面积(一)
小学 / 数学 / 北师大版 / 六年级上册
求下面图形中涂色部分的周长。
大圆弧长度:
2×3.14×4÷2=12.56(cm)
小圆弧长度:
2×3.14×3÷2=9.42(cm)
右侧线段长度:
3-(4-3)=2(cm)
左侧线段长度:
4 cm
12.56+9.42+2+4=27.98(cm)
阴影部分周长:
思路点拨:分析与圆相关的图形周长时,要注意观察图形周长中包含几条圆弧,几条线段。图中阴影部分周长包括大小两个圆周长的一半,一条大圆的半径和右侧的一条线段(线段长度与两个圆的半径有关)。
例题1:
求下面图形中涂色部分的周长。
大圆弧长度:
2×3.14×2÷2=6.28(cm)
小圆弧长度:
2×3.14÷2=3.14(cm)
大圆半径:
2 cm
阴影部分的周长:
6.28+3.14+2=11.42(cm)
练一练:
思路点拨:已知小圆的直径,可以分别算出红蚂蚁和黑蚂蚁爬行的路程,通过比较就可以知道谁爬的路程多了。
例题2:
两只小蚂蚁在下图中寻找食物。红蚂蚁从A点出发,沿着大圆爬了一圈回到A点。黑蚂蚁也从A点出发,沿着内部的8字形爬了一圈回到A点。如果每个小圆的直径都是10米,算一算,谁爬的路程多?
红蚂蚁:
黑蚂蚁:
2×3.14×10=62.8(m)
3.14×10+3.14×10=62.8(m)
62.8=62.8
答:两只蚂蚁爬的路程相等。
例题2:
(2)如果黑蚂蚁的行走路线如下图所示,小圆直径8米,中圆直径12米,那么请问谁爬的路程多?
两只小蚂蚁在下图中寻找食物。红蚂蚁从A点出发,沿着大圆爬了一圈回到A点。黑蚂蚁也从A点出发,沿着内部的8字形爬了一圈回到A点。
红蚂蚁:
3.14×(8+12)=62.8(m)
黑蚂蚁:
3.14×8+3.14×12=62.8(m)
62.8=62.8
答:两只蚂蚁爬的路程相等。
例题2:
两个行走路线不同,两只蚂蚁的路程和都相等,你有什么发现?
2×3.14×10=62.8
3.14×10+3.14×10=62.8
发现:两个小圆的直径和等于大圆的直径时,
小圆的周长和与大圆的周长相等。
3.14×(8+12)=62.8
3.14×8+3.14×12=62.8
如果大圆中的小圆数量增加,这个结论仍然成立。
例题2:
如果都变成半圆呢?
1、计算下面图形阴影部分的周长。(单位:cm)
3.14×(3+5)=25.12(cm)
练一练:
8cm
2、计算下面图形的周长。(单位:cm)
3.14×8×2=50.24(cm)
练一练:
求下面图形中涂色部分的周长。
3.14×2×2=12.56(cm)
思路点拨:彩绳长度包括4段圆弧和4条线段的长度。每段圆弧都是以4厘米为直径圆的四分之一,合在一起正好是一个整圆周长,4条线段正好是4条直径的长度。
例题3:
把四个圆柱形的薯片筒用彩绳捆在一起(底面如下图),捆一圈至少用彩绳多少厘米?(接头处忽略不计)
4条圆弧长度和:
3.14×4=12.56(cm)
4条线段长度和:
4×4=16(cm)
彩绳长度:
12.56+16=28.56(cm)
答:捆一圈至少用彩绳28.56厘米。
超市促销一种饮料,促销包装如下图。已知每个饮料瓶的外直径都是8厘米,每个促销包装上下各捆1圈绳子,打结处都需要10厘米的绳子。要包装一个这样的促销包装至少需要多长的绳子?
练一练:
4条圆弧长度和:
3.14×8=25.12(cm)
4条线段长度和:
打结处长度:
8×6=48(cm)
10 cm
(25,12+48+10)×2
=83.12×2
=166.24(cm)
绳子总长度:
答:包装一个这样的促销包装至少需要166.24厘米的绳子。
思路点拨:跑一圈多少米就是求这个图形的周长,周长中包括两条直道的长度(2条线段),还有2条圆弧的长度(2条圆弧合起来是整圆的周长)。分别计算出来再相加即可。
例题4:
下图是学校操场的示意图(单位:米),绕着操场跑一圈至少要跑多少米?
2条直道长度和:
2条圆弧长度和:
跑道周长:
100×2=200(m)
3.14×60=188.4(m)
200+188.4=388.4(m)
答:至少要跑388.4米。
下图是一个运动场的跑道,围绕这个跑道跑一圈是400米,已知跑道两边的直道长130米,求跑道半圆部分的直径是多少米?(π取近似数3;结果保留一位小数)
练一练:
400-130×2=140(m)
140÷3≈46.7(m)
答:跑道半圆部分的直径约是46.7米。
下图中每个小圆的半径都是1cm,求阴影部分的周长。
例题5:
思路点拨:图中阴影部分的周长看似很复杂,仔细观察会发现,阴影部分的周长就是所有小圆的周长加上1个大圆的周长。通过已知条件“小圆的半径是1厘米”可知大圆的直径是1×2×3=6厘米。
小圆的周长和:
2×3.14×1×7=43.96(cm)
大圆的周长:
1×2×3=6(cm)
3.14×6=18.84(cm)
阴影部分的周长:
43.96+18.84=62.8(cm)
练一练:
下图中虚线正方形的边长是4cm,求阴影部分的周长。
4条圆弧长度和:
4条线段长度和:
阴影部分周长:
2×3.14×4=25.12(cm)
4×4=16(cm)
25.12+16=41.12(cm)
3.14×6÷2=9.42(cm)
6+2+2=10(cm)
3.14×10÷2=15.7(cm)
2+2=4(cm)
9.42+15.7+4=29.12(cm)
练一练:
计算下图阴影部分的周长。
课堂总结:
这节课有什么收获?
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
