2025秋高考数学复习第六章第七讲立体几何中的向量方法 课件(共67张PPT)
文档属性
| 名称 | 2025秋高考数学复习第六章第七讲立体几何中的向量方法 课件(共67张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 21:24:13 | ||
图片预览










文档简介
(共67张PPT)
第七讲 立体几何中的向量方法
1.能用向量方法解决点到直线、点到平面、相互平行的直线、
相互平行的平面的距离问题.
2.能用向量方法解决直线与直线、直线与平面、平面与平面的
夹角的计算问题.
3.体会向量方法在研究立体几何问题中的应用.
1.异面直线所成的角
若异面直线 l1,l2 所成的角为θ,其方向向量分别是 u,v,则
2.直线与平面所成的角
如图,直线 AB 与平面α相交于点 B,设直线 AB 与平面α所
成的角为θ,直线 AB 的方向向量为 u,平面α的法向量为 n,则
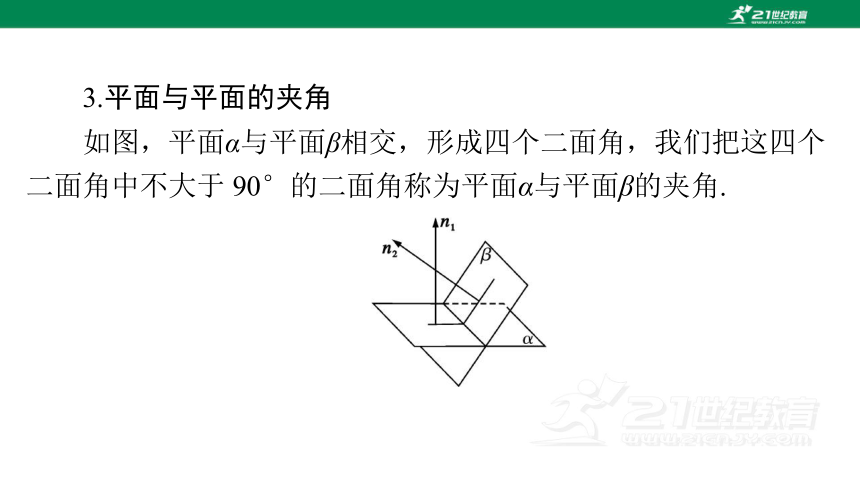
3.平面与平面的夹角
如图,平面α与平面β相交,形成四个二面角,我们把这四个
二面角中不大于 90°的二面角称为平面α与平面β的夹角.
若平面α,β的法向量分别是 n1 和 n2,则平面α与平面β的夹角
即为向量 n1 和 n2 的夹角或其补角.设平面α与平面β的夹角为θ,则
【常用结论】
(1)线面角θ的正弦值等于直线的方向向量 a 与平面的法向量 n
所成角的余弦值的绝对值,即 sin θ=|cos〈a,n〉|,不要误记为
cos θ=|cos〈a,n〉|.
(2)二面角的范围是[0,π],两个平面夹角的范围是
4.利用空间向量求距离
(1)点到直线的距离
(2)点到平面的距离
如图,已知平面α的法向量为 n,A 是平面α内
的定点,P 是平面α外一点.过点 P 作平面α的垂线l,
交平面α于点 Q,且 n 是直线 l 的方向向量,则点
(3)线面距、面面距均可转化为点面距进行求解.注意体积法在
求点到平面距离时的应用.
【名师点睛】
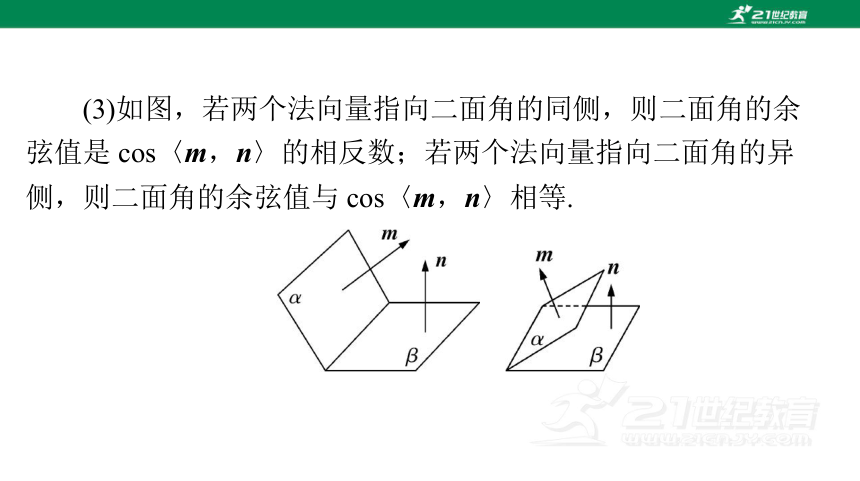
(3)如图,若两个法向量指向二面角的同侧,则二面角的余
弦值是 cos〈m,n〉的相反数;若两个法向量指向二面角的异
侧,则二面角的余弦值与 cos〈m,n〉相等.
考点一 利用向量求空间的角
考向 1 向量法求异面直线所成的角
答案:C
(2)有公共边的等边三角形 ABC 和 BCD 所在平面互相垂直,
则异面直线 AB 和 CD 所成角的余弦值为________.
解析:设等边三角形的边长为 2.取 BC 的中点 O,连接 OA,
OD.因为等边三角形 ABC 和 BCD 所在平面互相垂直,所以 OA,
OC,OD 两两垂直,以点 O 为坐标原点,OD,OC,OA所在直线
分别为 x 轴、y 轴、z 轴建立如图所示的空间直角坐标系.
【题后反思】
(1)求异面直线所成角的思路:
①选好基底或建立空间直角坐标系;
②求出两直线的方向向量 v1,v2;
(2)两异面直线所成角的关注点:
考向 2 向量法求线面角
(1)求证:MN∥平面 PBC;
(2)求证:平面 PBC⊥平面 ABCD;
(3)求 CM 与平面 PAD 所成角的正弦值.
∴MN∥BE.
∵MN 平面 PBC,BE 平面 PBC,
∴MN∥平面 PBC.
图 1
(3)解:建立如图 2 所示的空间直角坐标系,
图 2
【题后反思】
(1)求线面角的思路
①求出直线的方向向量 a 与平面的法向量 b;
考向 3 向量法求二面角
(1)证明:平面 PAD ⊥平面 ABCD;
(2)若点 E 为棱 PC 的中点,求平面 AEB 与平面 BCE 夹角的
余弦值.
(2)解:由(1)知 DC⊥平面 PAD ,
∴DC⊥DA.
∴底面 ABCD 为正方形.
设 AD 的中点为 O,连接 OP,在平面 ABCD 内作 OF∥DC
交BC 于点 F,
∵△PAD 为等边三角形,
∴PO⊥AD.
∴PO⊥平面 ABCD.
如图,以O为坐标原点,OA,OF,OP所在直线分别为 x 轴、
y 轴、z 轴,建立空间直角坐标系.
【题后反思】利用向量法确定二面角大小的常用方法
(1)找法向量法:分别求出二面角的两个半平面所在平面的法
向量,然后通过两个平面的法向量的夹角得到二面角的大小,但
要注意结合实际图形判断所求角的大小.
(2)找与棱垂直的方向向量法:分别在二面角的两个半平面内
找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角
的大小就是二面角的大小.
【考法全练】
1.如图,在边长是 4 的正方体 ABCD-A1B1C1D1 中,E,F 分别
为 AB,A1C 的中点,则直线 EF 与 CD1 所成角的大小为________.
解析:以 D 为坐标原点,DA,DC,DD1 所在直线分别为 x
轴、y 轴、z 轴,建立如图所示的空间直角坐标系.
则 D(0,0,0),A1(4,0,4),C(0,4,0),E(4,2,0),
F(2,2,2),D1(0,0,4),
2.已知三棱柱 ABC-A1B1C1 的侧棱与底面边长都相等,A1 在底
面 ABC 上的射影为△ABC 的中心,则 AB1 与底面 ABC 所成角的
正弦值为__________.
(1)证明:∵PA ⊥平面 ABCD,AD 平面 ABCD,
∴PA ⊥AD,
又∵AD⊥PB,PB∩PA =P,PB,PA 面 PAB,
∴AD⊥平面 PAB ,
又 AB 平面 PAB ,
∴AD⊥AB,
在△ABC 中,AB2+BC2=AC2,
∴AB⊥BC,
∵A,B,C,D 四点共面,
∴AD∥BC,
又∵BC 平面 PBC,AD 平面 PBC,
∴AD∥平面 PBC.
(2)解:以 DA,DC 为 x 轴、y 轴,过点 D 作平面 ABCD 垂直
的线为 z 轴,建立如图所示的空间直角坐标系 Dxyz.
令 AD=t,则 A(t,0,0),P(t,0,2),D(0,0,0),
考点二 求空间距离
[例 4](2024 年天津卷)如图,在四棱柱 ABCD-A1B1C1D1 中,
AA1⊥平面ABCD,AB⊥AD,AB∥CD,AB=AA1=2,AD=DC=
1,M,N 分别为 DD1,B1C1 的中点.
(1)求证:D1N∥平面 CB1M;
(2)求平面 CB1M 与平面 BB1C1C 夹角的
余弦值;
(3)求点 B 到平面 CB1M 的距离.
又 ME 平面 CB1M,D1N 平面 CB1M,
∴D1N∥平面 CB1M.
【题后反思】求点到平面的距离的常用方法
(1)直接法:过 P 点作平面α的垂线,垂足为 Q,把 PQ 放在某
个三角形中,用解三角形方法求出的 PQ 的长度就是点 P 到平面α
的距离.
(2)转化法:若点 P 所在的直线 l 平行于平面α,则可转化为求
直线 l 上某一个点到平面α的距离.
(3)等体积法:把点到面的距离转化为某个三棱锥的高,先利
用其他方法求出该三棱锥的体积与底面积,进而求得三棱锥的高.
(4)向量法:设平面α的一个法向量为 n,A 是平面α内任意一
点,则点 P 到平面α的距离为 d=
【变式训练】
1.如图,P 为矩形 ABCD 所在平面外一点,PA ⊥平面 ABCD.
若已知 AB =3 ,AD =4 ,PA =1 ,则点 P 到直线 BD 的距离为
________.
解析:如图,分别以 AB,AD,AP 所在直线为 x 轴、y 轴、
z 轴建立空间直角坐标系,
则 P(0,0,1),B(3,0,0),D(0,4,0),
2.(2023年天津卷)如图,在三棱台ABC A1B1C1中,若A1A⊥平面ABC,AB⊥AC,AB=AC=AA1=2,A1C1=1,M,N分别为BC,AB的中点.
(1)求证:A1N∥平面C1MA;
(2)求平面C1MA与平面ACC1A1所成角的余弦值;
(3)求点C到平面C1MA的距离.
(2)解:以 A 为原点,AB,AC,AA1 所在直线分别为 x 轴、
y 轴、z 轴,建立如图所示的空间直角坐标系.
由题知 A(0,0,0),B(2,0,0),C(0,2,0),M(1,1,0),
C1(0,1,2).
第七讲 立体几何中的向量方法
1.能用向量方法解决点到直线、点到平面、相互平行的直线、
相互平行的平面的距离问题.
2.能用向量方法解决直线与直线、直线与平面、平面与平面的
夹角的计算问题.
3.体会向量方法在研究立体几何问题中的应用.
1.异面直线所成的角
若异面直线 l1,l2 所成的角为θ,其方向向量分别是 u,v,则
2.直线与平面所成的角
如图,直线 AB 与平面α相交于点 B,设直线 AB 与平面α所
成的角为θ,直线 AB 的方向向量为 u,平面α的法向量为 n,则
3.平面与平面的夹角
如图,平面α与平面β相交,形成四个二面角,我们把这四个
二面角中不大于 90°的二面角称为平面α与平面β的夹角.
若平面α,β的法向量分别是 n1 和 n2,则平面α与平面β的夹角
即为向量 n1 和 n2 的夹角或其补角.设平面α与平面β的夹角为θ,则
【常用结论】
(1)线面角θ的正弦值等于直线的方向向量 a 与平面的法向量 n
所成角的余弦值的绝对值,即 sin θ=|cos〈a,n〉|,不要误记为
cos θ=|cos〈a,n〉|.
(2)二面角的范围是[0,π],两个平面夹角的范围是
4.利用空间向量求距离
(1)点到直线的距离
(2)点到平面的距离
如图,已知平面α的法向量为 n,A 是平面α内
的定点,P 是平面α外一点.过点 P 作平面α的垂线l,
交平面α于点 Q,且 n 是直线 l 的方向向量,则点
(3)线面距、面面距均可转化为点面距进行求解.注意体积法在
求点到平面距离时的应用.
【名师点睛】
(3)如图,若两个法向量指向二面角的同侧,则二面角的余
弦值是 cos〈m,n〉的相反数;若两个法向量指向二面角的异
侧,则二面角的余弦值与 cos〈m,n〉相等.
考点一 利用向量求空间的角
考向 1 向量法求异面直线所成的角
答案:C
(2)有公共边的等边三角形 ABC 和 BCD 所在平面互相垂直,
则异面直线 AB 和 CD 所成角的余弦值为________.
解析:设等边三角形的边长为 2.取 BC 的中点 O,连接 OA,
OD.因为等边三角形 ABC 和 BCD 所在平面互相垂直,所以 OA,
OC,OD 两两垂直,以点 O 为坐标原点,OD,OC,OA所在直线
分别为 x 轴、y 轴、z 轴建立如图所示的空间直角坐标系.
【题后反思】
(1)求异面直线所成角的思路:
①选好基底或建立空间直角坐标系;
②求出两直线的方向向量 v1,v2;
(2)两异面直线所成角的关注点:
考向 2 向量法求线面角
(1)求证:MN∥平面 PBC;
(2)求证:平面 PBC⊥平面 ABCD;
(3)求 CM 与平面 PAD 所成角的正弦值.
∴MN∥BE.
∵MN 平面 PBC,BE 平面 PBC,
∴MN∥平面 PBC.
图 1
(3)解:建立如图 2 所示的空间直角坐标系,
图 2
【题后反思】
(1)求线面角的思路
①求出直线的方向向量 a 与平面的法向量 b;
考向 3 向量法求二面角
(1)证明:平面 PAD ⊥平面 ABCD;
(2)若点 E 为棱 PC 的中点,求平面 AEB 与平面 BCE 夹角的
余弦值.
(2)解:由(1)知 DC⊥平面 PAD ,
∴DC⊥DA.
∴底面 ABCD 为正方形.
设 AD 的中点为 O,连接 OP,在平面 ABCD 内作 OF∥DC
交BC 于点 F,
∵△PAD 为等边三角形,
∴PO⊥AD.
∴PO⊥平面 ABCD.
如图,以O为坐标原点,OA,OF,OP所在直线分别为 x 轴、
y 轴、z 轴,建立空间直角坐标系.
【题后反思】利用向量法确定二面角大小的常用方法
(1)找法向量法:分别求出二面角的两个半平面所在平面的法
向量,然后通过两个平面的法向量的夹角得到二面角的大小,但
要注意结合实际图形判断所求角的大小.
(2)找与棱垂直的方向向量法:分别在二面角的两个半平面内
找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角
的大小就是二面角的大小.
【考法全练】
1.如图,在边长是 4 的正方体 ABCD-A1B1C1D1 中,E,F 分别
为 AB,A1C 的中点,则直线 EF 与 CD1 所成角的大小为________.
解析:以 D 为坐标原点,DA,DC,DD1 所在直线分别为 x
轴、y 轴、z 轴,建立如图所示的空间直角坐标系.
则 D(0,0,0),A1(4,0,4),C(0,4,0),E(4,2,0),
F(2,2,2),D1(0,0,4),
2.已知三棱柱 ABC-A1B1C1 的侧棱与底面边长都相等,A1 在底
面 ABC 上的射影为△ABC 的中心,则 AB1 与底面 ABC 所成角的
正弦值为__________.
(1)证明:∵PA ⊥平面 ABCD,AD 平面 ABCD,
∴PA ⊥AD,
又∵AD⊥PB,PB∩PA =P,PB,PA 面 PAB,
∴AD⊥平面 PAB ,
又 AB 平面 PAB ,
∴AD⊥AB,
在△ABC 中,AB2+BC2=AC2,
∴AB⊥BC,
∵A,B,C,D 四点共面,
∴AD∥BC,
又∵BC 平面 PBC,AD 平面 PBC,
∴AD∥平面 PBC.
(2)解:以 DA,DC 为 x 轴、y 轴,过点 D 作平面 ABCD 垂直
的线为 z 轴,建立如图所示的空间直角坐标系 Dxyz.
令 AD=t,则 A(t,0,0),P(t,0,2),D(0,0,0),
考点二 求空间距离
[例 4](2024 年天津卷)如图,在四棱柱 ABCD-A1B1C1D1 中,
AA1⊥平面ABCD,AB⊥AD,AB∥CD,AB=AA1=2,AD=DC=
1,M,N 分别为 DD1,B1C1 的中点.
(1)求证:D1N∥平面 CB1M;
(2)求平面 CB1M 与平面 BB1C1C 夹角的
余弦值;
(3)求点 B 到平面 CB1M 的距离.
又 ME 平面 CB1M,D1N 平面 CB1M,
∴D1N∥平面 CB1M.
【题后反思】求点到平面的距离的常用方法
(1)直接法:过 P 点作平面α的垂线,垂足为 Q,把 PQ 放在某
个三角形中,用解三角形方法求出的 PQ 的长度就是点 P 到平面α
的距离.
(2)转化法:若点 P 所在的直线 l 平行于平面α,则可转化为求
直线 l 上某一个点到平面α的距离.
(3)等体积法:把点到面的距离转化为某个三棱锥的高,先利
用其他方法求出该三棱锥的体积与底面积,进而求得三棱锥的高.
(4)向量法:设平面α的一个法向量为 n,A 是平面α内任意一
点,则点 P 到平面α的距离为 d=
【变式训练】
1.如图,P 为矩形 ABCD 所在平面外一点,PA ⊥平面 ABCD.
若已知 AB =3 ,AD =4 ,PA =1 ,则点 P 到直线 BD 的距离为
________.
解析:如图,分别以 AB,AD,AP 所在直线为 x 轴、y 轴、
z 轴建立空间直角坐标系,
则 P(0,0,1),B(3,0,0),D(0,4,0),
2.(2023年天津卷)如图,在三棱台ABC A1B1C1中,若A1A⊥平面ABC,AB⊥AC,AB=AC=AA1=2,A1C1=1,M,N分别为BC,AB的中点.
(1)求证:A1N∥平面C1MA;
(2)求平面C1MA与平面ACC1A1所成角的余弦值;
(3)求点C到平面C1MA的距离.
(2)解:以 A 为原点,AB,AC,AA1 所在直线分别为 x 轴、
y 轴、z 轴,建立如图所示的空间直角坐标系.
由题知 A(0,0,0),B(2,0,0),C(0,2,0),M(1,1,0),
C1(0,1,2).
同课章节目录
