2025秋高考数学复习第四章第一讲数列的概念与简单表示法课件(共30张PPT)
文档属性
| 名称 | 2025秋高考数学复习第四章第一讲数列的概念与简单表示法课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 944.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 10:24:45 | ||
图片预览











文档简介
(共30张PPT)
第四章
数列
第一讲 数列的概念与简单表示法
1.了解数列的概念和几种简单的表示方法(列表、图象、通项
公式).
2.了解数列是自变量为正整数的一类特殊函数.
概念 含义
数列 按照一定顺序排列的一列数
数列的项 数列中的每一个数
数列的通项 数列{an}的第n项an
通项公式 如果数列{an}的第n项an与序号n之间的关系能用公式
an=f(n)表示,这个公式叫做数列的通项公式
前n项和 在数列{an}中,Sn=a1+a2+…+an叫做数列的前n项和
1.数列的有关概念
列表法 列表格表示n与an的对应关系
图象法 把点(n,an)画在平面直角坐标系中
公
式
法 通项公式 把数列的通项用公式表示
递推公式 使用初始值a1和an+1=f(an)或a1,a2和an+1=f(an,an-1)等表示数列的方法
2.数列的表示方法
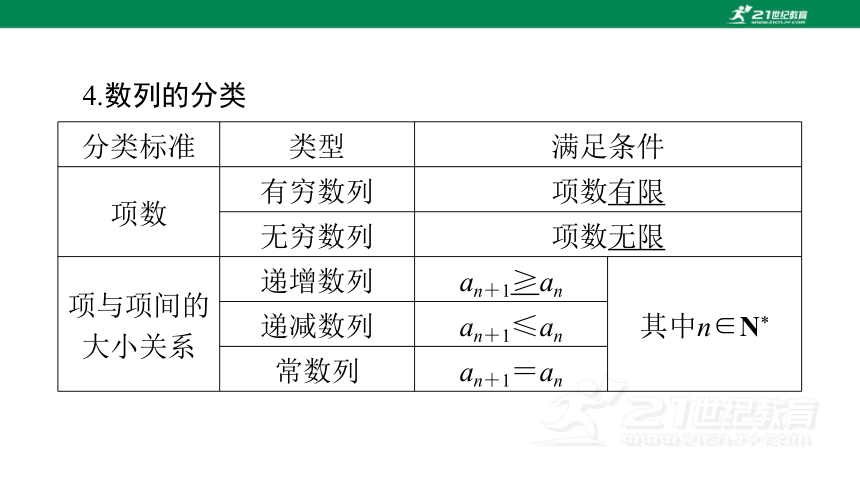
分类标准 类型 满足条件
项数 有穷数列 项数有限
无穷数列 项数无限
项与项间的
大小关系 递增数列 an+1≥an 其中n∈N*
递减数列 an+1≤an
常数列 an+1=an
4.数列的分类
考点一 由an与Sn的关系求通项
答案:C
答案:D
【题后反思】处理an与Sn的关系的方法
(1)代入n=1,直接求出a1的值或求出a1与a2的关系.
(2)若Sn易从等式中分离,则把等式中的n等量代换为n-1,利用Sn-Sn-1=an两式作差,否则直接代入an=Sn-Sn-1.
(3)注意a1的值不能通过公式an=Sn-Sn-1求出,若a1的值不满足该公式,则需用分段的形式表示数列的通项公式.
【变式训练】
1.已知Sn=2n+3,则an=______________.
考点二 数列的性质
考向 1 数列的单调性
A.是递增数列
C.先递增后递减
B.是递减数列
D.先递减后递增
答案:A
答案:8
考向 2 数列的周期性
[例3]已知数列{an}满足:an+1=an-an-1(n≥2,n∈N*),a1=
1,a2=2,Sn为数列{an}的前n项和,则S2 024=( )
A.3
B.2
C.1
D.0
解析:∵an+1=an-an-1,a1=1,a2=2,∴a3=1,a4=-1,
a5=-2,a6=-1,a7=1,a8=2,…,故数列{an}是周期为6的
周期数列,且每连续 6 项的和为 0.故 S2 024=337×0+3=3.故选 A.
答案:A
考向 3 数列的最值
[例 4]已知等差数列{an}的前n项和为Sn,且Sm-1=-2,
Sm=0,Sm+1=3(m≥2),则nSn的最小值为( )
A.-3
B.-5
C.-6
D.-9
答案:D
【题后反思】
(1)解决数列周期性问题的方法:先根据已知条件求出数列的
前几项,确定数列的周期,再根据周期性求值.
(2)判断数列单调性的方法:①作差(或商)法;②目标函数法:
写出数列对应的函数,利用导数或利用基本初等函数的单调性探
求其单调性,再将函数的单调性对应到数列中去.
【考法全练】
1.数列{an}的通项公式为an=2n2+tn+2,已知其为单调递增
)
数列,则 t 的取值范围为(
A.[-4,+∞)
B.(-6,+∞)
C.[-6,+∞)
D.(-∞,-4)
解析:∵an=2n2+tn+2,
答案:B
∴an+1=2(n+1)2+t(n+1)+2=2n2+4n+2+tn+t+2,
则an+1-an=4n+2+t.
∵{an}是递增数列,
∴4n+2+t>0恒成立,
即t>-4n-2恒成立,
∵n是正整数,
∴t>-6.即t∈(-6,+∞).故选B.
2.若数列{an}满足a1=1,a2=3,anan-2=an-1(n≥3),记数列{an}的前n项积为Tn,则下列说法错误的是( )
A.Tn无最大值 B.an有最大值
C.T2 024=3 D.a2 024=3
答案:A
3.(2024年河南焦作一模)已知数列{an}中,a1=1,且an+1(an
+1)+1=0,则{an}的前12项和为________.
答案:-6
第四章
数列
第一讲 数列的概念与简单表示法
1.了解数列的概念和几种简单的表示方法(列表、图象、通项
公式).
2.了解数列是自变量为正整数的一类特殊函数.
概念 含义
数列 按照一定顺序排列的一列数
数列的项 数列中的每一个数
数列的通项 数列{an}的第n项an
通项公式 如果数列{an}的第n项an与序号n之间的关系能用公式
an=f(n)表示,这个公式叫做数列的通项公式
前n项和 在数列{an}中,Sn=a1+a2+…+an叫做数列的前n项和
1.数列的有关概念
列表法 列表格表示n与an的对应关系
图象法 把点(n,an)画在平面直角坐标系中
公
式
法 通项公式 把数列的通项用公式表示
递推公式 使用初始值a1和an+1=f(an)或a1,a2和an+1=f(an,an-1)等表示数列的方法
2.数列的表示方法
分类标准 类型 满足条件
项数 有穷数列 项数有限
无穷数列 项数无限
项与项间的
大小关系 递增数列 an+1≥an 其中n∈N*
递减数列 an+1≤an
常数列 an+1=an
4.数列的分类
考点一 由an与Sn的关系求通项
答案:C
答案:D
【题后反思】处理an与Sn的关系的方法
(1)代入n=1,直接求出a1的值或求出a1与a2的关系.
(2)若Sn易从等式中分离,则把等式中的n等量代换为n-1,利用Sn-Sn-1=an两式作差,否则直接代入an=Sn-Sn-1.
(3)注意a1的值不能通过公式an=Sn-Sn-1求出,若a1的值不满足该公式,则需用分段的形式表示数列的通项公式.
【变式训练】
1.已知Sn=2n+3,则an=______________.
考点二 数列的性质
考向 1 数列的单调性
A.是递增数列
C.先递增后递减
B.是递减数列
D.先递减后递增
答案:A
答案:8
考向 2 数列的周期性
[例3]已知数列{an}满足:an+1=an-an-1(n≥2,n∈N*),a1=
1,a2=2,Sn为数列{an}的前n项和,则S2 024=( )
A.3
B.2
C.1
D.0
解析:∵an+1=an-an-1,a1=1,a2=2,∴a3=1,a4=-1,
a5=-2,a6=-1,a7=1,a8=2,…,故数列{an}是周期为6的
周期数列,且每连续 6 项的和为 0.故 S2 024=337×0+3=3.故选 A.
答案:A
考向 3 数列的最值
[例 4]已知等差数列{an}的前n项和为Sn,且Sm-1=-2,
Sm=0,Sm+1=3(m≥2),则nSn的最小值为( )
A.-3
B.-5
C.-6
D.-9
答案:D
【题后反思】
(1)解决数列周期性问题的方法:先根据已知条件求出数列的
前几项,确定数列的周期,再根据周期性求值.
(2)判断数列单调性的方法:①作差(或商)法;②目标函数法:
写出数列对应的函数,利用导数或利用基本初等函数的单调性探
求其单调性,再将函数的单调性对应到数列中去.
【考法全练】
1.数列{an}的通项公式为an=2n2+tn+2,已知其为单调递增
)
数列,则 t 的取值范围为(
A.[-4,+∞)
B.(-6,+∞)
C.[-6,+∞)
D.(-∞,-4)
解析:∵an=2n2+tn+2,
答案:B
∴an+1=2(n+1)2+t(n+1)+2=2n2+4n+2+tn+t+2,
则an+1-an=4n+2+t.
∵{an}是递增数列,
∴4n+2+t>0恒成立,
即t>-4n-2恒成立,
∵n是正整数,
∴t>-6.即t∈(-6,+∞).故选B.
2.若数列{an}满足a1=1,a2=3,anan-2=an-1(n≥3),记数列{an}的前n项积为Tn,则下列说法错误的是( )
A.Tn无最大值 B.an有最大值
C.T2 024=3 D.a2 024=3
答案:A
3.(2024年河南焦作一模)已知数列{an}中,a1=1,且an+1(an
+1)+1=0,则{an}的前12项和为________.
答案:-6
同课章节目录
