2025秋高考数学复习第一章第三讲全称量词与存在量词课件(共31张PPT)
文档属性
| 名称 | 2025秋高考数学复习第一章第三讲全称量词与存在量词课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 834.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 10:25:00 | ||
图片预览











文档简介
(共31张PPT)
第三讲 全称量词与存在量词
1.理解全称量词与存在量词的意义.
2.能正确地对全称量词命题或存在量词命题进行否定.
量词名称 常见量词 表示符号
全称量词 所有、一切、任意、全部、每一个、任给等
存在量词 存在一个、至少有一个、有一个、某个、有
些、某些等
1.全称量词与存在量词
命题名称 命题结构 命题简记
全称量词命题 对 M 中任意一个 x,有 p(x)成立 x∈M,p(x)
全称量词命题
的否定 存在 M 中的一个 x,使 p(x)不成立 x∈M, p(x)
存在量词命题 存在 M 中的一个 x,使 p(x)成立 x∈M,p(x)
存在量词命题
的否定 对 M 中任意一个 x,p(x)均不成立 x∈M, p(x)
2.全称量词命题与存在量词命题
3.全称量词命题和存在量词命题真假的判断
(1)全称量词命题为真,严格证明;全称量词命题为假,列举
反例;
(2)存在量词命题为真,列举特例;存在量词命题为假,严格
证明.
【常用结论】
含有一个量词的命题的否定的规律是“改量词,否结论”.
考点一 全称量词命题、存在量词命题
考向 1 全称量词命题、存在量词命题的否定
通性通法:(1)改量词:确定命题所含量词的类型,省去量词
的要结合命题的含义加上量词,再对量词进行改写.
(2)否结论:对原命题的结论进行否定.
答案:D
解析:命题“ x>0,x2>x3”的否定是“ x>0,x2≤x3”.
答案:B
(2)(2024年甘肃庆阳阶段练习)命题“ x>0,x2>x3”的否定是( )
A. x>0,x2>x3 B. x>0,x2≤x3
C. x≤0,x2≤x3 D. x>0,x2≤x3
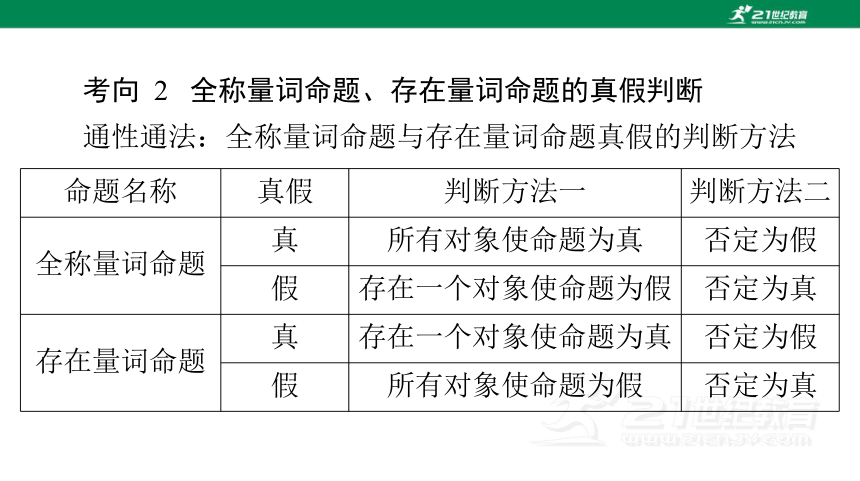
命题名称 真假 判断方法一 判断方法二
全称量词命题 真 所有对象使命题为真 否定为假
假 存在一个对象使命题为假 否定为真
存在量词命题 真 存在一个对象使命题为真 否定为假
假 所有对象使命题为假 否定为真
考向 2 全称量词命题、存在量词命题的真假判断
通性通法:全称量词命题与存在量词命题真假的判断方法
提醒:因为命题 p 与 p 的真假性相反,因此不管是全称量词
命题,还是存在量词命题,若其真假不容易正面判断时,可先判
断其否定的真假.
)
[例 2](1)下列命题中是假命题的是(
A.对任意 x∈R,x2≥0
B.对任意 x∈R,2x-1>0
C.存在 x∈R,lg x<1
D.存在 x∈R,sin x+cos x=2
答案:D
(2)(2024 年广东东莞期中考)下列命题中,是全称量词命题且
为真命题的是(
)
A.梯形是四边形
B. x∈R,x3+1≠0
C. x∈R,|x|+1≥1
D.存在一个实数 x,使 x2+2x-3=0
解析:对于 A,是全称量词命题且为真命题,A 选项正确;
对于 B,是全称量词命题,但当 x=-1 时,x3+1=0,命题
为假命题,B 选项错误;
C,D 选项都为存在量词命题,不合题意.
答案:A
【考法全练】
1.(多选题)下列命题的否定中,是全称量词命题且为真命题的
是(
)
B.所有的正方形都是矩形
C. x∈R,x2+2x+2=0
D.至少有一个实数 x,使 x3+1=0
答案:AC
2.(2024 年江西期中考)命题 p:“ x∈R,x2-x>10”的否定
是___________________.
解析:“ x∈R,x2-x>10”的否定是“ x∈R,x2-x≤10”.
答案: x∈R,x2-x≤10
考点二 根据命题真假求参数范围
[例 3] (2024年吉林期中考)已知集合A={x|0≤x≤a},集合
B={x|m2+3≤x≤m2+4},若命题“ m∈R,A∩B≠ ”为假命
题,则实数 a 的取值范围为(
A.{a|a<4}
C.{a|3)
B.{a|a<3}
D.{a|0答案:B
【题后反思】(1)全称量词命题可转化为恒成立问题,存在量
词命题可转化为能成立问题.
(2)含量词的命题中参数的取值范围,可根据命题的含义,转
化为函数的最值解决.
【变式训练】
⊙双变量“存在性或任意性”问题
解决双变量“存在性或任意性”问题的关键就是将含有全称
量词和存在量词的条件“等价”转化为两个函数值域之间的关系
(或两个函数最值之间的关系),目的在于培养学生的逻辑推理素养
和良好的数学思维品质.
【反思感悟】理解全称量词与存在量词的含义是求解本题的
关键,此类问题求解的策略是“等价转化”,即“函数 f(x)的值域
是 g(x)的值域的子集”从而利用包含关系求解.
【高分训练】
2.(2024年北京期中考)对 a∈[-1,1],f(x)=x2+(a-4)x+
)
4-2a 的值恒大于零,则 x 的取值范围是(
A.(-∞,1)∪(3,+∞)
B.(1,3)
C.(-∞,1)∪(2,+∞)
D.(1,2)
答案:A
第三讲 全称量词与存在量词
1.理解全称量词与存在量词的意义.
2.能正确地对全称量词命题或存在量词命题进行否定.
量词名称 常见量词 表示符号
全称量词 所有、一切、任意、全部、每一个、任给等
存在量词 存在一个、至少有一个、有一个、某个、有
些、某些等
1.全称量词与存在量词
命题名称 命题结构 命题简记
全称量词命题 对 M 中任意一个 x,有 p(x)成立 x∈M,p(x)
全称量词命题
的否定 存在 M 中的一个 x,使 p(x)不成立 x∈M, p(x)
存在量词命题 存在 M 中的一个 x,使 p(x)成立 x∈M,p(x)
存在量词命题
的否定 对 M 中任意一个 x,p(x)均不成立 x∈M, p(x)
2.全称量词命题与存在量词命题
3.全称量词命题和存在量词命题真假的判断
(1)全称量词命题为真,严格证明;全称量词命题为假,列举
反例;
(2)存在量词命题为真,列举特例;存在量词命题为假,严格
证明.
【常用结论】
含有一个量词的命题的否定的规律是“改量词,否结论”.
考点一 全称量词命题、存在量词命题
考向 1 全称量词命题、存在量词命题的否定
通性通法:(1)改量词:确定命题所含量词的类型,省去量词
的要结合命题的含义加上量词,再对量词进行改写.
(2)否结论:对原命题的结论进行否定.
答案:D
解析:命题“ x>0,x2>x3”的否定是“ x>0,x2≤x3”.
答案:B
(2)(2024年甘肃庆阳阶段练习)命题“ x>0,x2>x3”的否定是( )
A. x>0,x2>x3 B. x>0,x2≤x3
C. x≤0,x2≤x3 D. x>0,x2≤x3
命题名称 真假 判断方法一 判断方法二
全称量词命题 真 所有对象使命题为真 否定为假
假 存在一个对象使命题为假 否定为真
存在量词命题 真 存在一个对象使命题为真 否定为假
假 所有对象使命题为假 否定为真
考向 2 全称量词命题、存在量词命题的真假判断
通性通法:全称量词命题与存在量词命题真假的判断方法
提醒:因为命题 p 与 p 的真假性相反,因此不管是全称量词
命题,还是存在量词命题,若其真假不容易正面判断时,可先判
断其否定的真假.
)
[例 2](1)下列命题中是假命题的是(
A.对任意 x∈R,x2≥0
B.对任意 x∈R,2x-1>0
C.存在 x∈R,lg x<1
D.存在 x∈R,sin x+cos x=2
答案:D
(2)(2024 年广东东莞期中考)下列命题中,是全称量词命题且
为真命题的是(
)
A.梯形是四边形
B. x∈R,x3+1≠0
C. x∈R,|x|+1≥1
D.存在一个实数 x,使 x2+2x-3=0
解析:对于 A,是全称量词命题且为真命题,A 选项正确;
对于 B,是全称量词命题,但当 x=-1 时,x3+1=0,命题
为假命题,B 选项错误;
C,D 选项都为存在量词命题,不合题意.
答案:A
【考法全练】
1.(多选题)下列命题的否定中,是全称量词命题且为真命题的
是(
)
B.所有的正方形都是矩形
C. x∈R,x2+2x+2=0
D.至少有一个实数 x,使 x3+1=0
答案:AC
2.(2024 年江西期中考)命题 p:“ x∈R,x2-x>10”的否定
是___________________.
解析:“ x∈R,x2-x>10”的否定是“ x∈R,x2-x≤10”.
答案: x∈R,x2-x≤10
考点二 根据命题真假求参数范围
[例 3] (2024年吉林期中考)已知集合A={x|0≤x≤a},集合
B={x|m2+3≤x≤m2+4},若命题“ m∈R,A∩B≠ ”为假命
题,则实数 a 的取值范围为(
A.{a|a<4}
C.{a|3
B.{a|a<3}
D.{a|0
【题后反思】(1)全称量词命题可转化为恒成立问题,存在量
词命题可转化为能成立问题.
(2)含量词的命题中参数的取值范围,可根据命题的含义,转
化为函数的最值解决.
【变式训练】
⊙双变量“存在性或任意性”问题
解决双变量“存在性或任意性”问题的关键就是将含有全称
量词和存在量词的条件“等价”转化为两个函数值域之间的关系
(或两个函数最值之间的关系),目的在于培养学生的逻辑推理素养
和良好的数学思维品质.
【反思感悟】理解全称量词与存在量词的含义是求解本题的
关键,此类问题求解的策略是“等价转化”,即“函数 f(x)的值域
是 g(x)的值域的子集”从而利用包含关系求解.
【高分训练】
2.(2024年北京期中考)对 a∈[-1,1],f(x)=x2+(a-4)x+
)
4-2a 的值恒大于零,则 x 的取值范围是(
A.(-∞,1)∪(3,+∞)
B.(1,3)
C.(-∞,1)∪(2,+∞)
D.(1,2)
答案:A
同课章节目录
