2025秋高考数学复习第九章第八讲离散型随机变量的数字特征课件(共50张PPT)
文档属性
| 名称 | 2025秋高考数学复习第九章第八讲离散型随机变量的数字特征课件(共50张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 00:00:00 | ||
图片预览











文档简介
(共50张PPT)
第八讲 离散型随机变量的数字特征
1.理解取有限个值的离散型随机变量的均值、方差的概念.
2.会求简单离散型随机变量的均值、方差,并能利用离散型随
机变量的均值、方差解决一些简单实际问题.
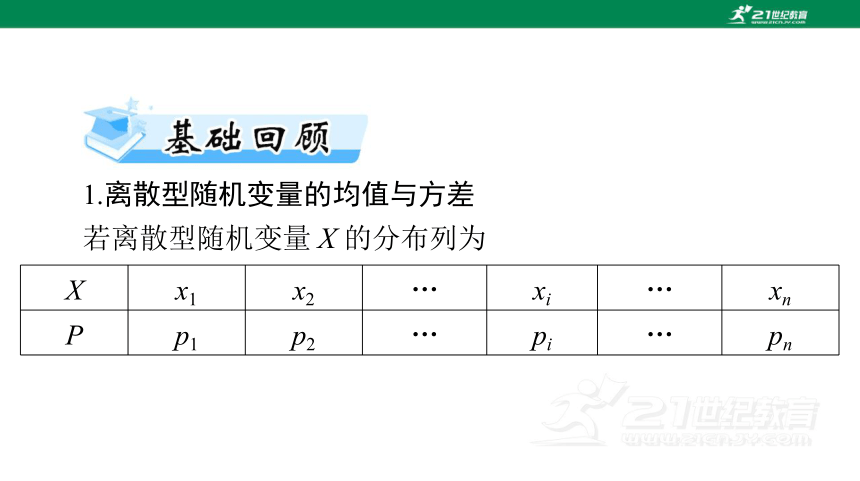
X x1 x2 … xi … xn
P p1 p2 … pi … pn
1.离散型随机变量的均值与方差
若离散型随机变量 X 的分布列为
(1)均值
2.均值与方差的性质
(1)E(aX+b)=aE(X)+b.
(2)D(aX+b)=a2D(X).(a,b 为常数)
3.两点分布、二项分布与超几何分布的数字特征
(1)若 X 服从两点分布,则 E(X)=p,D(X)=p(1-p).
(2)若 X~B(n,p),则 E(X)=np,D(X)=np(1-p).
(3)若 X 为从包含 M 件次品的 N 件产品中,不放回地随机抽取
【名师点睛】均值与方差的性质
(1)E(aX+b)=aE(X)+b.
(2)D(aX+b)=a2D(X)(a,b 为常数).
【常用结论】
均值与方差的四个常用性质
(1)E(k)=k,D(k)=0,其中 k 为常数.
(2)E(X1+X2)=E(X1)+E(X2).
(3)D(X)=E(X2)-(E(X))2.
(4)若 X1,X2 相互独立,则 E(X1X2)=E(X1)·E(X2).
考点一 离散型随机变量的均值与方差
[例1](1)“四书”是《大学》《中庸》《论语》《孟子》的合称,
在中国思想史上产生过深远影响.为弘扬中华优秀传统文化,某校
计划开展“四书”诵读比赛活动,某班有 4 名同学参赛,每人从
《大学》《中庸》《论语》《孟子》这4本书中选取 1 本进行准备,
且各自选取的书均不相同.比赛时,若这 4 名同学从这 4 本书中随
机抽取 1 本选择其中的内容诵读,则抽到自己准备的书的学生人
数的数学期望为(
)
A.
1
2
B.1
2
C.
3
D.2
答案:B
(2)(2024 年河北联考)某芯片公司生产甲、乙、丙 3 种型号的
芯片,每种芯片均需要 2 次光刻才能成型,甲、乙、丙芯片第 1
次光刻的良品率分别为 75%,80%,100%.只有第 1 次光刻为良品,
才能进行第 2 次光刻,否则为废品被淘汰,而甲、乙、丙芯片第 2
次光刻的良品率分别为 80%,75%,60%.第 2 次光刻的良品才是
合格品.
①从甲、乙、丙 3 种芯片的第 1 次光刻产品中各任取 1 件,
若恰有 2 件是良品,求甲芯片是良品的概率;
②甲、乙、丙 3 种芯片的每件合格品可为公司赚取利润 150
元,每件不合格品使公司赔 50 元,现生产甲、乙、丙芯片各 1 件,
设这 3 件芯片为公司赚取的利润为 X(单位:元),求 X 的分布列、
数学期望与方差.
解:①设事件 Ai,Bi,Ci(i=1,2)分别为甲、乙、丙 3 种芯片
第 i 次光刻为良品,
则P(A1)=0.75,P(A2)=0.8,P(B1)=0.8,P(B2)=0.75,
P(C1)=1,P(C2)=0.6.
丙芯片第 1 次光刻肯定是良品,故恰有 2 件良品是甲、丙或
乙、丙,
所以甲芯片是良品的概率是
【题后反思】求离散型随机变量ξ的均值与方差的步骤
(1)理解ξ的意义,写出ξ可能的全部取值.
(2)求ξ取每个值的概率.
(3)写出ξ的分布列.
(4)由均值、方差的定义求 E(ξ),D(ξ).
【变式训练】
1.(2024 年天津模拟)已知一个不透明的袋中有大小、质地相同
的 4 个红球、3 个白球和 2 个黑球.若不放回地摸球,每次摸 1 个
球,摸取 4 次,则恰有 3 次摸到红球的概率为________;若有放
回地摸球,每次摸 1 个球,摸取 3 次,则摸到红球的次数 X 的期
望为________.
2.一袋子中有除颜色外完全相同的 3 个白球和4个黑球,现从
袋中往外取球,每次任取 1 个球,记下颜色后放回,取球 7 次,
设取得的白球数为 X,则 D(X)=(
)
答案:C
考点二 均值与方差在决策问题中的应用
[例 2](2024 年江苏南京月考)在一次知识竞赛中,参赛选手应
从 8 个不同的题目中随机抽取 3 个题目进行作答.已知这 8 个题目
中,选手甲只能正确作答其中的 6 个,而选手乙正确作答每个题
目的概率均为 0.75,且甲、乙两位选手对每个题目作答都是相互
独立的.
(1)记选手甲正确作答的题目的个数为 X,乙正确作答的题目
的个数为 Y,求 X,Y 的分布列.
(2)结合你所学过的概率知识说明,甲、乙两名选手谁更优秀?
【题后反思】离散型随机变量的期望和方差应用问题的解题
策略
实际问题中,若两个随机变量ξ1,ξ2,有 E(ξ1)=E(ξ2)或 E(ξ1)
与 E(ξ2)较为接近时,就需要用 D(ξ1)与 D(ξ2)来比较两个随机变量
的稳定程度.一般将期望最大(或最小)的方案作为最优方案.若各方
案的期望相同,则选择方差最小(或最大)的方案作为最优方案.
【变式训练】
(2024 年福建南平期末考)某公司举办联欢晚会,为活跃气氛,
计划举行抽奖活动,有两种方案.
方案一:不放回地从装有 2 个红球和 4 个白球的箱子中随机
抽出 3 个球,每抽出 1 个红球奖励 100 元.
方案二:有放回地从装有 2 个红球和 4 个白球的箱子中随机
抽出 3 个球,每抽出 1 个红球奖励 100 元.
分别用随机变量 X,Y(单位:元)表示某员工按方案一和方案
二抽奖的获奖金额.
(1)求随机变量 X 的分布列和数学期望.
(2)用统计知识分析,为使公司员工获奖金额相对均衡,应选
择哪种方案?请说明理由.
⊙利用分类讨论思想求数学期望
[例3](2024 年四川内江一模)某市为全面提高青少年健康素养
水平,举办了一次“健康素养知识竞赛”,分预赛和复赛两个环
节,预赛成绩采用百分制,排名前 300 名的学生参加复赛.已知共
有 10 000 名学生参加了预赛,现从参加预赛的全体学生中随机地
抽取 100 人的预赛成绩作为样本,得到如下频率分布直方图.
(1)规定预赛成绩不低于 80 分为优良,若从上述样本中预赛成
绩不低于 70 分的学生中随机地抽取 2 人,求至少有 1 人预赛成绩
优良的概率.
(2)由频率分布直方图,可认为该市全体参加预赛学生的预赛
成绩 Z 近似服从正态分布 N(μ,σ2),其中μ可近似为样本中的 100
名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),
且σ2=214,已知小明的预赛成绩为 95 分,利用该正态分布,估
计小明是否有资格参加复赛?
(3)复赛规则如下:①复赛题目由 A,B 两类问题组成,答对
A 类问题得 30 分,不答或答错得 0 分;答对 B 类问题得 70 分,
不答或答错得 0 分.②A,B 两类问题的答题顺序可由参赛学生选
择,但只有在答对第一类问题的情况下,才有资格答第二类问题.
已知参加复赛的学生甲答对 A 类问题的概率为 0.8,答对 B 类问
题的概率为0.6,答对每类问题相互独立,且与答题顺序无关.为使
累计得分的期望最大,学生甲应选择先答哪类问题?并说明理由.
取 2 人,至少有 1 人预赛成绩优良的概率为
解:(1)由题意可知抽取的 100 人中预赛成绩不低于 80 分的人
数为 100×10×(0.012+0.005)=17,
预赛成绩不低于 70 分的学生人数为 17+100×10×0.016=
33,
因此,从上述样本中预赛成绩不低于 70 分的学生中随机地抽
X 0 30 100
P 0.2 0.32 0.48
(3)若学生甲先答 A 类问题,设他的得分为随机变量 X,则 X
的可能取值有 0,30,100,
P(X=0)=0.2,P(X=30)=0.8×0.4=0.32,P(X=100)=
0.8×0.6=0.48,
所以随机变量 X 的分布列如下表所示.
E(X)=0×0.2+30×0.32+100×0.48=57.6.
Y 0 70 100
P 0.4 0.12 0.48
若学生甲先答 B 类问题,设他的得分为随机变量 Y,则 Y 的
可能取值有 0,70,100,
P(X=0)=0.2,P(X=30)=0.8×0.4=0.32,P(X=100)=
0.6×0.8=0.48,
所以随机变量 Y 的分布列如表所示.
E(Y)=0×0.4+70×0.12+100×0.48=56.4.
因为 E(X)>E(Y),所以学生甲应先答 A 类问题.
【高分训练】
(1)记甲在一天内参加“四人赛”和“双人对战”两项活动
(两项活动均只参加一局)的总得分为X,求X的分布列与数学期望;
(2)“挑战答题”比赛规则如下:每位参赛者每次连续回答 5 道
题,在答对的情况下可以持续答题,若第一次答错时,答题结束,
积分为 0 分,只有全部答对 5 道题可以获得 5 个积分.该学习平台为
了吸引更多人参与答题,设置了一个“得积分进阶”活动,从 1 阶
到 n(n≥10)阶,规定每轮答题获得 5 个积分进 2 阶,没有获得积分
进 1 阶,按照获得的阶级给予相应的奖品.若乙每次获得 5 个积分的
第八讲 离散型随机变量的数字特征
1.理解取有限个值的离散型随机变量的均值、方差的概念.
2.会求简单离散型随机变量的均值、方差,并能利用离散型随
机变量的均值、方差解决一些简单实际问题.
X x1 x2 … xi … xn
P p1 p2 … pi … pn
1.离散型随机变量的均值与方差
若离散型随机变量 X 的分布列为
(1)均值
2.均值与方差的性质
(1)E(aX+b)=aE(X)+b.
(2)D(aX+b)=a2D(X).(a,b 为常数)
3.两点分布、二项分布与超几何分布的数字特征
(1)若 X 服从两点分布,则 E(X)=p,D(X)=p(1-p).
(2)若 X~B(n,p),则 E(X)=np,D(X)=np(1-p).
(3)若 X 为从包含 M 件次品的 N 件产品中,不放回地随机抽取
【名师点睛】均值与方差的性质
(1)E(aX+b)=aE(X)+b.
(2)D(aX+b)=a2D(X)(a,b 为常数).
【常用结论】
均值与方差的四个常用性质
(1)E(k)=k,D(k)=0,其中 k 为常数.
(2)E(X1+X2)=E(X1)+E(X2).
(3)D(X)=E(X2)-(E(X))2.
(4)若 X1,X2 相互独立,则 E(X1X2)=E(X1)·E(X2).
考点一 离散型随机变量的均值与方差
[例1](1)“四书”是《大学》《中庸》《论语》《孟子》的合称,
在中国思想史上产生过深远影响.为弘扬中华优秀传统文化,某校
计划开展“四书”诵读比赛活动,某班有 4 名同学参赛,每人从
《大学》《中庸》《论语》《孟子》这4本书中选取 1 本进行准备,
且各自选取的书均不相同.比赛时,若这 4 名同学从这 4 本书中随
机抽取 1 本选择其中的内容诵读,则抽到自己准备的书的学生人
数的数学期望为(
)
A.
1
2
B.1
2
C.
3
D.2
答案:B
(2)(2024 年河北联考)某芯片公司生产甲、乙、丙 3 种型号的
芯片,每种芯片均需要 2 次光刻才能成型,甲、乙、丙芯片第 1
次光刻的良品率分别为 75%,80%,100%.只有第 1 次光刻为良品,
才能进行第 2 次光刻,否则为废品被淘汰,而甲、乙、丙芯片第 2
次光刻的良品率分别为 80%,75%,60%.第 2 次光刻的良品才是
合格品.
①从甲、乙、丙 3 种芯片的第 1 次光刻产品中各任取 1 件,
若恰有 2 件是良品,求甲芯片是良品的概率;
②甲、乙、丙 3 种芯片的每件合格品可为公司赚取利润 150
元,每件不合格品使公司赔 50 元,现生产甲、乙、丙芯片各 1 件,
设这 3 件芯片为公司赚取的利润为 X(单位:元),求 X 的分布列、
数学期望与方差.
解:①设事件 Ai,Bi,Ci(i=1,2)分别为甲、乙、丙 3 种芯片
第 i 次光刻为良品,
则P(A1)=0.75,P(A2)=0.8,P(B1)=0.8,P(B2)=0.75,
P(C1)=1,P(C2)=0.6.
丙芯片第 1 次光刻肯定是良品,故恰有 2 件良品是甲、丙或
乙、丙,
所以甲芯片是良品的概率是
【题后反思】求离散型随机变量ξ的均值与方差的步骤
(1)理解ξ的意义,写出ξ可能的全部取值.
(2)求ξ取每个值的概率.
(3)写出ξ的分布列.
(4)由均值、方差的定义求 E(ξ),D(ξ).
【变式训练】
1.(2024 年天津模拟)已知一个不透明的袋中有大小、质地相同
的 4 个红球、3 个白球和 2 个黑球.若不放回地摸球,每次摸 1 个
球,摸取 4 次,则恰有 3 次摸到红球的概率为________;若有放
回地摸球,每次摸 1 个球,摸取 3 次,则摸到红球的次数 X 的期
望为________.
2.一袋子中有除颜色外完全相同的 3 个白球和4个黑球,现从
袋中往外取球,每次任取 1 个球,记下颜色后放回,取球 7 次,
设取得的白球数为 X,则 D(X)=(
)
答案:C
考点二 均值与方差在决策问题中的应用
[例 2](2024 年江苏南京月考)在一次知识竞赛中,参赛选手应
从 8 个不同的题目中随机抽取 3 个题目进行作答.已知这 8 个题目
中,选手甲只能正确作答其中的 6 个,而选手乙正确作答每个题
目的概率均为 0.75,且甲、乙两位选手对每个题目作答都是相互
独立的.
(1)记选手甲正确作答的题目的个数为 X,乙正确作答的题目
的个数为 Y,求 X,Y 的分布列.
(2)结合你所学过的概率知识说明,甲、乙两名选手谁更优秀?
【题后反思】离散型随机变量的期望和方差应用问题的解题
策略
实际问题中,若两个随机变量ξ1,ξ2,有 E(ξ1)=E(ξ2)或 E(ξ1)
与 E(ξ2)较为接近时,就需要用 D(ξ1)与 D(ξ2)来比较两个随机变量
的稳定程度.一般将期望最大(或最小)的方案作为最优方案.若各方
案的期望相同,则选择方差最小(或最大)的方案作为最优方案.
【变式训练】
(2024 年福建南平期末考)某公司举办联欢晚会,为活跃气氛,
计划举行抽奖活动,有两种方案.
方案一:不放回地从装有 2 个红球和 4 个白球的箱子中随机
抽出 3 个球,每抽出 1 个红球奖励 100 元.
方案二:有放回地从装有 2 个红球和 4 个白球的箱子中随机
抽出 3 个球,每抽出 1 个红球奖励 100 元.
分别用随机变量 X,Y(单位:元)表示某员工按方案一和方案
二抽奖的获奖金额.
(1)求随机变量 X 的分布列和数学期望.
(2)用统计知识分析,为使公司员工获奖金额相对均衡,应选
择哪种方案?请说明理由.
⊙利用分类讨论思想求数学期望
[例3](2024 年四川内江一模)某市为全面提高青少年健康素养
水平,举办了一次“健康素养知识竞赛”,分预赛和复赛两个环
节,预赛成绩采用百分制,排名前 300 名的学生参加复赛.已知共
有 10 000 名学生参加了预赛,现从参加预赛的全体学生中随机地
抽取 100 人的预赛成绩作为样本,得到如下频率分布直方图.
(1)规定预赛成绩不低于 80 分为优良,若从上述样本中预赛成
绩不低于 70 分的学生中随机地抽取 2 人,求至少有 1 人预赛成绩
优良的概率.
(2)由频率分布直方图,可认为该市全体参加预赛学生的预赛
成绩 Z 近似服从正态分布 N(μ,σ2),其中μ可近似为样本中的 100
名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),
且σ2=214,已知小明的预赛成绩为 95 分,利用该正态分布,估
计小明是否有资格参加复赛?
(3)复赛规则如下:①复赛题目由 A,B 两类问题组成,答对
A 类问题得 30 分,不答或答错得 0 分;答对 B 类问题得 70 分,
不答或答错得 0 分.②A,B 两类问题的答题顺序可由参赛学生选
择,但只有在答对第一类问题的情况下,才有资格答第二类问题.
已知参加复赛的学生甲答对 A 类问题的概率为 0.8,答对 B 类问
题的概率为0.6,答对每类问题相互独立,且与答题顺序无关.为使
累计得分的期望最大,学生甲应选择先答哪类问题?并说明理由.
取 2 人,至少有 1 人预赛成绩优良的概率为
解:(1)由题意可知抽取的 100 人中预赛成绩不低于 80 分的人
数为 100×10×(0.012+0.005)=17,
预赛成绩不低于 70 分的学生人数为 17+100×10×0.016=
33,
因此,从上述样本中预赛成绩不低于 70 分的学生中随机地抽
X 0 30 100
P 0.2 0.32 0.48
(3)若学生甲先答 A 类问题,设他的得分为随机变量 X,则 X
的可能取值有 0,30,100,
P(X=0)=0.2,P(X=30)=0.8×0.4=0.32,P(X=100)=
0.8×0.6=0.48,
所以随机变量 X 的分布列如下表所示.
E(X)=0×0.2+30×0.32+100×0.48=57.6.
Y 0 70 100
P 0.4 0.12 0.48
若学生甲先答 B 类问题,设他的得分为随机变量 Y,则 Y 的
可能取值有 0,70,100,
P(X=0)=0.2,P(X=30)=0.8×0.4=0.32,P(X=100)=
0.6×0.8=0.48,
所以随机变量 Y 的分布列如表所示.
E(Y)=0×0.4+70×0.12+100×0.48=56.4.
因为 E(X)>E(Y),所以学生甲应先答 A 类问题.
【高分训练】
(1)记甲在一天内参加“四人赛”和“双人对战”两项活动
(两项活动均只参加一局)的总得分为X,求X的分布列与数学期望;
(2)“挑战答题”比赛规则如下:每位参赛者每次连续回答 5 道
题,在答对的情况下可以持续答题,若第一次答错时,答题结束,
积分为 0 分,只有全部答对 5 道题可以获得 5 个积分.该学习平台为
了吸引更多人参与答题,设置了一个“得积分进阶”活动,从 1 阶
到 n(n≥10)阶,规定每轮答题获得 5 个积分进 2 阶,没有获得积分
进 1 阶,按照获得的阶级给予相应的奖品.若乙每次获得 5 个积分的
同课章节目录
