2025秋高考数学复习第九章第六讲离散型随机变量及其分布列课件(共33张PPT)
文档属性
| 名称 | 2025秋高考数学复习第九章第六讲离散型随机变量及其分布列课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 00:00:00 | ||
图片预览










文档简介
(共33张PPT)
第六讲 离散型随机变量及其分布列
1.理解离散型随机变量及其分布列的概念,了解分布列对于刻
画随机现象的重要性.
2.理解超几何分布及其推导过程,并能解决简单的实际问题.
1.离散型随机变量
一般地,对于随机试验样本空间Ω中的每个样本点ω,都有唯
一的实数 X(ω)与之对应,我们称 X 为随机变量.可能取值为有限个
或可以一一列举的随机变量称为离散型随机变量.
X x1 x2 … xi … xn
P p1 p2 … pi … pn
2.离散型随机变量的分布列及性质
(1)一般地,若离散型随机变量X的可能取值为x1,x2,…,xi,…,xn,X取每一个值xi的概率P(X=xi)=pi(i=1,2,…,n)为离散型随机变量X的概率分布列,简称分布列.离散型随机变量X的分布列可用下表表示:
(2)离散型随机变量的分布列的性质:
①pi≥0(i=1,2,…,n);②p1+p2+…+pn=1.
X 0 1
P 1-p p
3.两点分布和超几何分布
(1)两点分布
若随机变量X的分布列如下表所示:
则称X服从两点分布,并称p=P(X=1)为成功概率.
【名师点睛】利用分布列中各概率之和为 1 可求参数的值,
此时要注意检验,以保证每个概率值均为非负数.
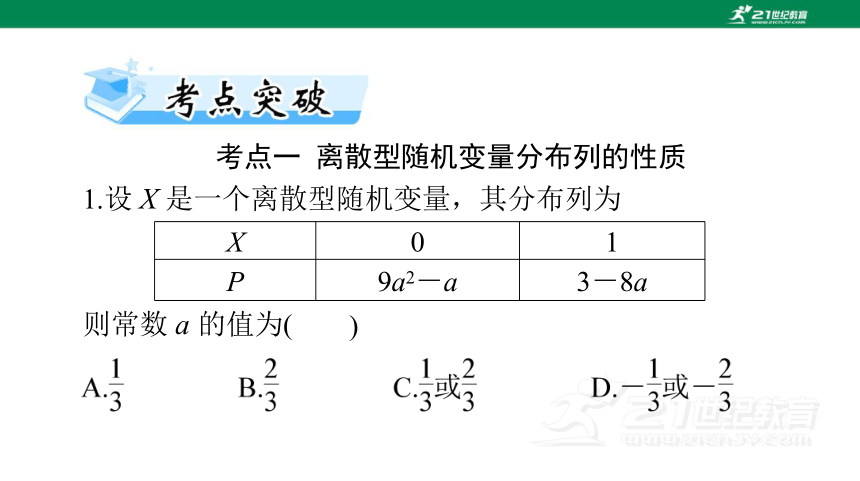
X 0 1
P 9a2-a 3-8a
考点一 离散型随机变量分布列的性质
1.设 X 是一个离散型随机变量,其分布列为
则常数 a 的值为(
)
答案:A
答案:C
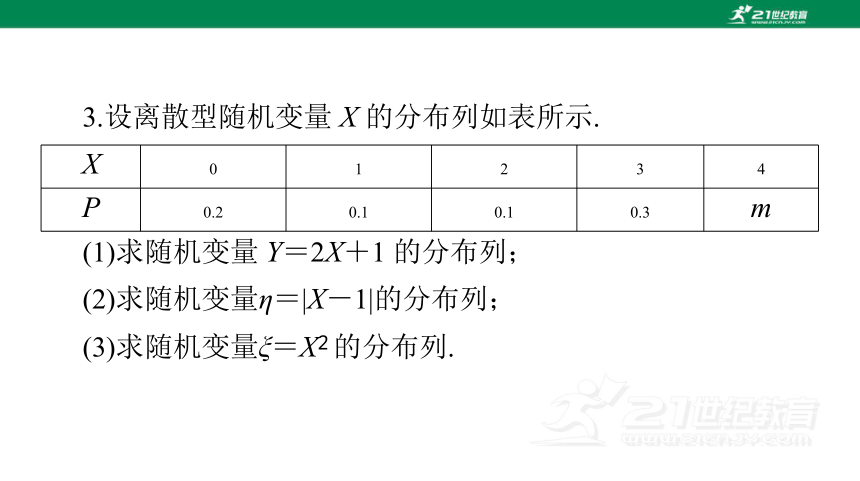
X 0 1 2 3 4
P 0.2 0.1 0.1 0.3 m
3.设离散型随机变量 X 的分布列如表所示.
(1)求随机变量 Y=2X+1 的分布列;
(2)求随机变量η=|X-1|的分布列;
(3)求随机变量ξ=X2 的分布列.
X 0 1 2 3 4
2X+1 1 3 5 7 9
Y 1 3 5 7 9
P 0.2 0.1 0.1 0.3 0.3
解:(1)由分布列的性质知,0.2+0.1+0.1+0.3+m=1,解得
m=0.3.
首先列表如下.
从而随机变量 Y=2X+1 的分布列如表所示.
X 0 1 2 3 4
|X-1| 1 0 1 2 3
η 0 1 2 3
P 0.1 0.3 0.3 0.3
(2)列表如下.
∴P(η=0)=P(X=1)=0.1,
P(η=1)=P(X=0)+P(X=2)=0.2+0.1=0.3,
P(η=2)=P(X=3)=0.3,
P(η=3)=P(X=4)=0.3.
故随机变量η=|X-1|的分布列如表所示.
ξ 0 1 4 9 16
P 0.2 0.1 0.1 0.3 0.3
X 0 1 2 3 4
X2 0 1 4 9 16
(3)列表如下.
从而随机变量ξ=X2 的分布列如表所示.
【题后反思】分布列性质的两个作用
(1)利用分布列中各事件概率之和为 1 可求参数的值及检查分
布列的正确性.
(2)随机变量 X 所取的值分别对应的事件是两两互斥的,利用
这一点可以求随机变量在某个范围内的概率.
考点二 求离散型随机变量的分布列
[例 1]某商场销售某种品牌的空调器,每周初购进一定数量的
空调器,商场每销售一台空调器可获利 500 元.若供大于求,则每
台多余的空调器需交保管费 100 元;若供不应求,则可从其他商
场调剂供应,此时每台空调器仅获利润 200 元.
(1)若该商场某周初购进 20 台空调器,求当周的利润(单位:
元)关于当周需求量 n(单位:台,n∈N)的函数解析式 f(n);
周需求量 n 18 19 20 21 22
频数 1 2 3 3 1
(2)该商场记录了去年夏天(共 10 周)的空调器周需求量 n(单
位:台,n∈N),整理得下表.
以记录的每周需求量的频率作为每周需求量的概率,若商场
某周初购进 20 台空调器,X 表示当周的利润(单位:元),求 X 的
分布列.
X 8 800 9 400 10 000 10 200 10 400
P 0.1 0.2 0.3 0.3 0.1
(2)由(1)得 f(18)=8 800,f(19)=9 400,f(20)=10 000,
f(21)=10 200,f(22)=10 400,
所以当周的利润 X 的所有可能取值分别为 8 800,9 400,
10 000,10 200,10 400,
易知 P(X=8 800)=0.1,P(X=9 400)=0.2,P(X=10 000)=
0.3, P(X=10 200)=0.3,P(X=10 400)=0.1.所以 X 的分布列为
【题后反思】离散型随机变量分布列的求解步骤
【变式训练】
一个盒子里装有 7 张卡片,其中红色卡片有 4 张,编号分别
为 1,2,3,4;白色卡片有 3 张,编号分别为 2,3,4.从盒子中
任取 4 张卡片(假设取到任何一张卡片的可能性相同).
(1)求取出的 4 张卡片中,含有编号为 3 的卡片的概率;
(2)在取出的 4 张卡片中,红色卡片编号的最大值设为 X,求
随机变量 X 的分布列.
所以随机变量 X 的分布列如下.
考点三 超几何分布
[例 2]端午节吃粽子是我国的传统习俗.设一盘中装有 10 个粽
子,其中豆沙粽 2 个,肉粽 3 个,白粽 5 个,这三种粽子的外观
完全相同.从中任意选取 3 个.
(1)求三种粽子各取到 1 个的概率;
(2)设 X 表示取到的豆沙粽个数,求 X 的分布列;
(3)求至少有一个豆沙粽的概率;
(4)设 Y 表示取到的粽子的种类,求 Y 的分布列.
综上可知,Y 的分布列如表所示.
【题后反思】求超几何分布的分布列的步骤
【变式训练】
在 10 件产品中,有 3 件一等品,4 件二等品,3 件三等品,
从这 10 件产品中任取 3 件,求:
(1)取出的 3 件产品中一等品件数 X 的分布列;
(2)取出的 3 件产品中一等品件数多于二等品件数的概率.
第六讲 离散型随机变量及其分布列
1.理解离散型随机变量及其分布列的概念,了解分布列对于刻
画随机现象的重要性.
2.理解超几何分布及其推导过程,并能解决简单的实际问题.
1.离散型随机变量
一般地,对于随机试验样本空间Ω中的每个样本点ω,都有唯
一的实数 X(ω)与之对应,我们称 X 为随机变量.可能取值为有限个
或可以一一列举的随机变量称为离散型随机变量.
X x1 x2 … xi … xn
P p1 p2 … pi … pn
2.离散型随机变量的分布列及性质
(1)一般地,若离散型随机变量X的可能取值为x1,x2,…,xi,…,xn,X取每一个值xi的概率P(X=xi)=pi(i=1,2,…,n)为离散型随机变量X的概率分布列,简称分布列.离散型随机变量X的分布列可用下表表示:
(2)离散型随机变量的分布列的性质:
①pi≥0(i=1,2,…,n);②p1+p2+…+pn=1.
X 0 1
P 1-p p
3.两点分布和超几何分布
(1)两点分布
若随机变量X的分布列如下表所示:
则称X服从两点分布,并称p=P(X=1)为成功概率.
【名师点睛】利用分布列中各概率之和为 1 可求参数的值,
此时要注意检验,以保证每个概率值均为非负数.
X 0 1
P 9a2-a 3-8a
考点一 离散型随机变量分布列的性质
1.设 X 是一个离散型随机变量,其分布列为
则常数 a 的值为(
)
答案:A
答案:C
X 0 1 2 3 4
P 0.2 0.1 0.1 0.3 m
3.设离散型随机变量 X 的分布列如表所示.
(1)求随机变量 Y=2X+1 的分布列;
(2)求随机变量η=|X-1|的分布列;
(3)求随机变量ξ=X2 的分布列.
X 0 1 2 3 4
2X+1 1 3 5 7 9
Y 1 3 5 7 9
P 0.2 0.1 0.1 0.3 0.3
解:(1)由分布列的性质知,0.2+0.1+0.1+0.3+m=1,解得
m=0.3.
首先列表如下.
从而随机变量 Y=2X+1 的分布列如表所示.
X 0 1 2 3 4
|X-1| 1 0 1 2 3
η 0 1 2 3
P 0.1 0.3 0.3 0.3
(2)列表如下.
∴P(η=0)=P(X=1)=0.1,
P(η=1)=P(X=0)+P(X=2)=0.2+0.1=0.3,
P(η=2)=P(X=3)=0.3,
P(η=3)=P(X=4)=0.3.
故随机变量η=|X-1|的分布列如表所示.
ξ 0 1 4 9 16
P 0.2 0.1 0.1 0.3 0.3
X 0 1 2 3 4
X2 0 1 4 9 16
(3)列表如下.
从而随机变量ξ=X2 的分布列如表所示.
【题后反思】分布列性质的两个作用
(1)利用分布列中各事件概率之和为 1 可求参数的值及检查分
布列的正确性.
(2)随机变量 X 所取的值分别对应的事件是两两互斥的,利用
这一点可以求随机变量在某个范围内的概率.
考点二 求离散型随机变量的分布列
[例 1]某商场销售某种品牌的空调器,每周初购进一定数量的
空调器,商场每销售一台空调器可获利 500 元.若供大于求,则每
台多余的空调器需交保管费 100 元;若供不应求,则可从其他商
场调剂供应,此时每台空调器仅获利润 200 元.
(1)若该商场某周初购进 20 台空调器,求当周的利润(单位:
元)关于当周需求量 n(单位:台,n∈N)的函数解析式 f(n);
周需求量 n 18 19 20 21 22
频数 1 2 3 3 1
(2)该商场记录了去年夏天(共 10 周)的空调器周需求量 n(单
位:台,n∈N),整理得下表.
以记录的每周需求量的频率作为每周需求量的概率,若商场
某周初购进 20 台空调器,X 表示当周的利润(单位:元),求 X 的
分布列.
X 8 800 9 400 10 000 10 200 10 400
P 0.1 0.2 0.3 0.3 0.1
(2)由(1)得 f(18)=8 800,f(19)=9 400,f(20)=10 000,
f(21)=10 200,f(22)=10 400,
所以当周的利润 X 的所有可能取值分别为 8 800,9 400,
10 000,10 200,10 400,
易知 P(X=8 800)=0.1,P(X=9 400)=0.2,P(X=10 000)=
0.3, P(X=10 200)=0.3,P(X=10 400)=0.1.所以 X 的分布列为
【题后反思】离散型随机变量分布列的求解步骤
【变式训练】
一个盒子里装有 7 张卡片,其中红色卡片有 4 张,编号分别
为 1,2,3,4;白色卡片有 3 张,编号分别为 2,3,4.从盒子中
任取 4 张卡片(假设取到任何一张卡片的可能性相同).
(1)求取出的 4 张卡片中,含有编号为 3 的卡片的概率;
(2)在取出的 4 张卡片中,红色卡片编号的最大值设为 X,求
随机变量 X 的分布列.
所以随机变量 X 的分布列如下.
考点三 超几何分布
[例 2]端午节吃粽子是我国的传统习俗.设一盘中装有 10 个粽
子,其中豆沙粽 2 个,肉粽 3 个,白粽 5 个,这三种粽子的外观
完全相同.从中任意选取 3 个.
(1)求三种粽子各取到 1 个的概率;
(2)设 X 表示取到的豆沙粽个数,求 X 的分布列;
(3)求至少有一个豆沙粽的概率;
(4)设 Y 表示取到的粽子的种类,求 Y 的分布列.
综上可知,Y 的分布列如表所示.
【题后反思】求超几何分布的分布列的步骤
【变式训练】
在 10 件产品中,有 3 件一等品,4 件二等品,3 件三等品,
从这 10 件产品中任取 3 件,求:
(1)取出的 3 件产品中一等品件数 X 的分布列;
(2)取出的 3 件产品中一等品件数多于二等品件数的概率.
同课章节目录
