2025秋高考数学复习第九章第三讲二项式定理课件
文档属性
| 名称 | 2025秋高考数学复习第九章第三讲二项式定理课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 10:35:53 | ||
图片预览











文档简介
(共43张PPT)
第三讲
二项式定理
1.能用多项式运算法则和计数原理证明二项式定理.
2.会用二项式定理解决与二项展开式有关的简单问题.
1.二项式定理
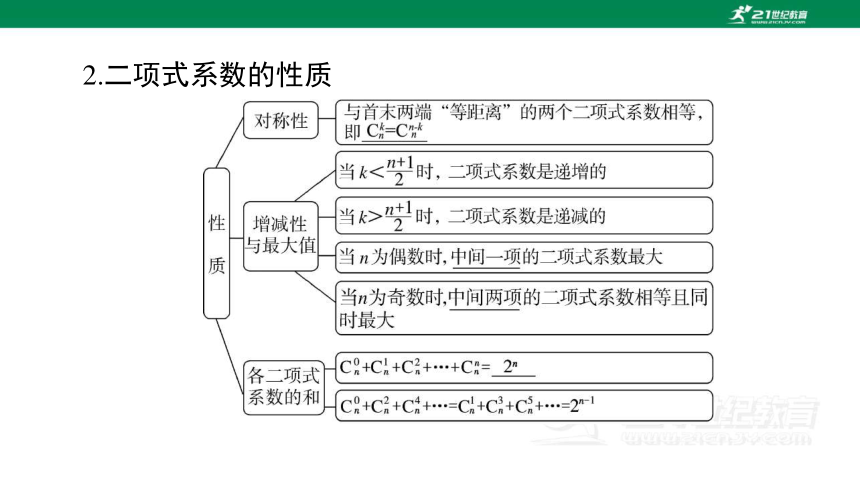
2.二项式系数的性质
【名师点睛】二项展开式形式上的特点
(1)项数为 n+1.
(2)各项的次数都等于二项式的幂指数 n,即 a 与 b 的指数的
和为 n.
(3)字母 a 按降幂排列,从第一项开始,次数由 n 逐项减1直到
0;字母 b 按升幂排列,从第一项开始,次数由 0 逐项加 1 直到n.
(4)(a+b)n的展开式与(b+a)n的展开式的项完全相同,但两个
展开式的通项不同.
(5)二项式系数与项的系数是完全不同的两个概念.二项式系
数是指 它只与各项的项数有关,而与 a,b
的值无关;项的系数是指该项中除变量外的常数部分,它不仅
与各项的项数有关,还与 a,b 的值有关.
考点一 二项展开式中的特定项或系数
A.-40
B.40
C.-80
D.80
答案:D
答案:BC
答案:6
【题后反思】与二项展开式有关问题的解题策略
(1)求展开式中的特定项,可依据条件写出第 r+1 项,再由特
定项的特点求出 r 的值即可.
(2)已知展开式的某项,求特定项的系数,可由某项得出参数
项,再由通项写出第 r+1 项,由特定项得出 r 的值,最后求出其
参数.
考点二 二项式系数的和与各项的系数和问题
答案:-160
(2)若(1-3x)5=a0+a1x+a2x2+…+a5x5,则a1+a2+a3+a4+
a5=__________.
解析:令x=1,则(1-3×1)5=a0+a1+a2+a3+a4+a5=-32,
令x=0,则(1-3×0)5=a0=1,
所以a1+a2+a3+a4+a5=a0+a1+a2+a3+a4+a5-a0=
-32-1=-33.
答案:-33
【题后反思】求解系数和问题常用的“赋值法”
赋值法是指对二项式中的未知元素赋值,从而求得二项展开
式的各项系数和的方法.求解有关系数和问题的关键点如下:
(1)赋值,观察已知等式与所求式子的结构特征,确定所赋的
值,常赋的值有-1,0,1 等.
(2)求参数,通过赋值,建立参数的相关方程,解方程,可得
参数值.
(3)求值,根据题意,得出指定项的系数和.
【变式训练】
1.(多选题)已知f(x)=(2x-3)n(n∈N*)展开式的二项式系数和为512,f(x)=a0+a1(x-1)+a2(x-1)2+…+an(x-1)n,下列选项正确的是( )
A.a1+a2+…+an=1
B.a1+2a2+3a3+…+nan=18
C.f(6)被8除的余数为1
D.|a0|+|a1|+…+|an|=39
答案:BCD
2.(2024 年上海普陀模拟)已知(1+x)n 展开式的各项系数之和
为 64,展开式中 x2 项的系数为________.
答案:15
考点三 二项式系数的性质
考向 1 二项式系数的最值问题
答案:-160
考向 2 项的系数的最值问题
答案:5
答案:1 013 或 1 014
⊙几个多项式的展开式问题
A.5
B.10
C.15
D.20
答案:C
[例 5](2x2-3x+a)5的展开式的各项系数之和为 1,则该展开
)
式中含 x7 项的系数是(
A.-600
C.-1 080
B.-840
D.-2 040
答案:D
【反思感悟】
(1)求解形如(a+b)m(c+d)n的展开式问题的思路
①若m,n中有一个比较小,可考虑把它展开,如(a+b)2(c+d)n=(a2+2ab+b2)(c+d)n,然后分别求解;
②观察(a+b)(c+d)是否可以合并,如(1+x)5(1-x)7=[(1+x)(1-x)]5(1-x)2=(1-x2)5(1-x)2.
(2)求解三项式问题的思路
①对于三项式问题,一般是通过合并、拆分或因式分解,转
化成二项式定理的形式去求解;或看成几个因式的乘积,再利用
组合数公式求解.
②求三项展开式的项时,可看作是把次数“分配”给不同的
【高分训练】
1.(2024 年江苏扬州期末考)(x-y)(x+y)8 的展开式中 x2y7 的系
数为(
)
A.20 B.-20 C.28 D.-28
答案:B
答案:D
第三讲
二项式定理
1.能用多项式运算法则和计数原理证明二项式定理.
2.会用二项式定理解决与二项展开式有关的简单问题.
1.二项式定理
2.二项式系数的性质
【名师点睛】二项展开式形式上的特点
(1)项数为 n+1.
(2)各项的次数都等于二项式的幂指数 n,即 a 与 b 的指数的
和为 n.
(3)字母 a 按降幂排列,从第一项开始,次数由 n 逐项减1直到
0;字母 b 按升幂排列,从第一项开始,次数由 0 逐项加 1 直到n.
(4)(a+b)n的展开式与(b+a)n的展开式的项完全相同,但两个
展开式的通项不同.
(5)二项式系数与项的系数是完全不同的两个概念.二项式系
数是指 它只与各项的项数有关,而与 a,b
的值无关;项的系数是指该项中除变量外的常数部分,它不仅
与各项的项数有关,还与 a,b 的值有关.
考点一 二项展开式中的特定项或系数
A.-40
B.40
C.-80
D.80
答案:D
答案:BC
答案:6
【题后反思】与二项展开式有关问题的解题策略
(1)求展开式中的特定项,可依据条件写出第 r+1 项,再由特
定项的特点求出 r 的值即可.
(2)已知展开式的某项,求特定项的系数,可由某项得出参数
项,再由通项写出第 r+1 项,由特定项得出 r 的值,最后求出其
参数.
考点二 二项式系数的和与各项的系数和问题
答案:-160
(2)若(1-3x)5=a0+a1x+a2x2+…+a5x5,则a1+a2+a3+a4+
a5=__________.
解析:令x=1,则(1-3×1)5=a0+a1+a2+a3+a4+a5=-32,
令x=0,则(1-3×0)5=a0=1,
所以a1+a2+a3+a4+a5=a0+a1+a2+a3+a4+a5-a0=
-32-1=-33.
答案:-33
【题后反思】求解系数和问题常用的“赋值法”
赋值法是指对二项式中的未知元素赋值,从而求得二项展开
式的各项系数和的方法.求解有关系数和问题的关键点如下:
(1)赋值,观察已知等式与所求式子的结构特征,确定所赋的
值,常赋的值有-1,0,1 等.
(2)求参数,通过赋值,建立参数的相关方程,解方程,可得
参数值.
(3)求值,根据题意,得出指定项的系数和.
【变式训练】
1.(多选题)已知f(x)=(2x-3)n(n∈N*)展开式的二项式系数和为512,f(x)=a0+a1(x-1)+a2(x-1)2+…+an(x-1)n,下列选项正确的是( )
A.a1+a2+…+an=1
B.a1+2a2+3a3+…+nan=18
C.f(6)被8除的余数为1
D.|a0|+|a1|+…+|an|=39
答案:BCD
2.(2024 年上海普陀模拟)已知(1+x)n 展开式的各项系数之和
为 64,展开式中 x2 项的系数为________.
答案:15
考点三 二项式系数的性质
考向 1 二项式系数的最值问题
答案:-160
考向 2 项的系数的最值问题
答案:5
答案:1 013 或 1 014
⊙几个多项式的展开式问题
A.5
B.10
C.15
D.20
答案:C
[例 5](2x2-3x+a)5的展开式的各项系数之和为 1,则该展开
)
式中含 x7 项的系数是(
A.-600
C.-1 080
B.-840
D.-2 040
答案:D
【反思感悟】
(1)求解形如(a+b)m(c+d)n的展开式问题的思路
①若m,n中有一个比较小,可考虑把它展开,如(a+b)2(c+d)n=(a2+2ab+b2)(c+d)n,然后分别求解;
②观察(a+b)(c+d)是否可以合并,如(1+x)5(1-x)7=[(1+x)(1-x)]5(1-x)2=(1-x2)5(1-x)2.
(2)求解三项式问题的思路
①对于三项式问题,一般是通过合并、拆分或因式分解,转
化成二项式定理的形式去求解;或看成几个因式的乘积,再利用
组合数公式求解.
②求三项展开式的项时,可看作是把次数“分配”给不同的
【高分训练】
1.(2024 年江苏扬州期末考)(x-y)(x+y)8 的展开式中 x2y7 的系
数为(
)
A.20 B.-20 C.28 D.-28
答案:B
答案:D
同课章节目录
