2025秋高考数学复习第三章第六讲函数y=Asin(ωx+φ)的图象及应用课件
文档属性
| 名称 | 2025秋高考数学复习第三章第六讲函数y=Asin(ωx+φ)的图象及应用课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 10:37:54 | ||
图片预览











文档简介
(共52张PPT)
第六讲 函数y=Asin(ωx+φ)的图象及应用
1.了解函数 y=A sin (ωx+φ)的物理意义;能画出函数的图象,
了解参数 A,ω,φ对函数图象变化的影响.
2.会用三角函数解决一些简单实际问题,体会三角函数是描述
周期变化现象的重要函数模型.
y=A sin (ωx+φ)(A>0,ω>0),x∈[0,+∞)
振幅 周期 频率 相位 初相
A ωx+φ φ
1.y=A sin (ωx+φ)的有关概念
2.“五点法”画 y=A sin (ωx+φ)的图象
用“五点法”画 y=A sin (ωx+φ)一个周期内的简图时,要找
五个特征点,如下表:
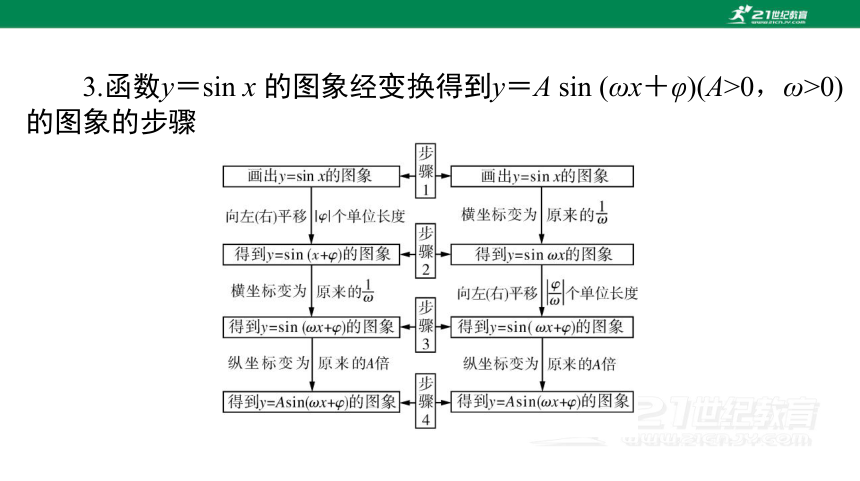
3.函数y=sin x 的图象经变换得到y=A sin (ωx+φ)(A>0,ω>0)
的图象的步骤
【常用结论】
(1)函数 y=A sin (ωx+φ)+k 图象平移的规律:“左加右减,
上加下减”.
(2)函数图象的左右平移本质上是 x 的增减变化.函数图象向左
平移α个单位长度时,只需把函数解析式中的 x 整体代换为 x+α
即可.
(3)函数图象上的点的横坐标的倍数变化本质上是 x 的倍数变
析式中的 x 整体代换为ωx 即可.
考点一 函数 y=A sin (ωx+φ)的图象及变换
答案:C
答案:B
令g(x)=f(x)+x=x-sin x,则g′(x)=1-cos x≥0对任意x∈R
恒成立,可知函数 y=g(x)在 R 上单调递增,且 g(0)=0,
所以函数 y=f(x)+x 的零点个数为 1.故选 B.
答案:B
【题后反思】由函数 y=sin x 的图象通过变换得到 y=Asin(ωx
+φ)的图象有两种途径:“先平移后伸缩”与“先伸缩后平移”.
提醒:三角函数图象左右平移时应注意的问题
①弄清楚平移方向,平移哪个函数的图象,得到哪个函数的
图象.
②注意平移前后两个函数的名称是否一致,若不一致,应先
利用诱导公式化为同名函数.
③由 y=Asin ωx 的图象得到 y=Asin (ωx+φ)的图象时,需平
移 个单位长度,而不是|φ|个单位长度.
考点二 根据函数图象求解析式
[例1](1)已知a是实数,则函数f(x)=1+asin ax的图象不可能
是(
)
A
B
C
D
答案:D
答案:ACD
【题后反思】确定 y=Asin (ωx+φ)+B(A>0,ω>0)的解析
式的步骤
(3)求φ,把图象上一个已知的极值点及其对应的函数值代入求
解;若代入的不是极值点,求解时需注意该点在递增区间上,还
是在递减区间上.
【变式训练】
答案:C
答案:B
考点三 三角函数图象与性质的综合应用
考向 1 函数 y=Asin (ωx+φ)的应用
考向 2 函数零点(方程根)问题
【题后反思】巧用图象解决三角函数相关的方程或不等式
问题
解决与三角函数相关的方程或不等式问题,最基本的方法就
是作出对应函数的图象,然后结合函数图象的特征确定方程的解
或不等式的解集.故准确作出对应函数在指定区间上的图象是解决
问题的关键.
【考法全练】
答案:B
答案:A
⊙三角函数在实际问题中的应用(数学建模)
[例4](2024年辽宁沈阳阶段练习)某游乐场的摩天轮示意图如
图,已知该摩天轮的半径为30 m,轮上最低点与地面的距离为2 m,
沿逆时针方向匀速旋转,旋转一周所需时间为 T=24 min.在圆周
上均匀分布 12 个座舱,标号分别为 1~12(可视为点),在旋转过
程中,座舱与地面的距离 h(单位:m)与时间 t(单位:min)的函数
关系基本符合正弦函数模型,现从图示位置,即 1 号座舱位于圆
周最右端时开始计时,旋转时间为 t min.
(1)求 1 号座舱与地面的距离 h 与时间 t 的函数 h(t)的解析式;
(2)在前 24 min 内,求 1 号座舱与地面的距离为 17 m 时 t 的值.
【高分训练】
阻尼器是一种以提供阻力达到减震效果的专业工程装置.由物
理学知识可知,某阻尼器的运动过程可近似为单摆运动,其离开
平衡位置的位移 y(单位:m)和时间 t(单位:s)的函数关系为 y=
sin (ωt+φ)(ω>0,|φ|<π),如图,若该阻尼器在摆动过程中连续
三次到达同一位置的时间分别为 t1,t2,t3(0<t1<t2<t3),且 t1+
t2=2,t2+t3=5,则在一个周期内阻尼器离开平衡位置的位移大于
0.5 m 的总时间为(
)
1
A. s
3
2
B. s
3
C.1 s
4
D. s
3
答案:C
第六讲 函数y=Asin(ωx+φ)的图象及应用
1.了解函数 y=A sin (ωx+φ)的物理意义;能画出函数的图象,
了解参数 A,ω,φ对函数图象变化的影响.
2.会用三角函数解决一些简单实际问题,体会三角函数是描述
周期变化现象的重要函数模型.
y=A sin (ωx+φ)(A>0,ω>0),x∈[0,+∞)
振幅 周期 频率 相位 初相
A ωx+φ φ
1.y=A sin (ωx+φ)的有关概念
2.“五点法”画 y=A sin (ωx+φ)的图象
用“五点法”画 y=A sin (ωx+φ)一个周期内的简图时,要找
五个特征点,如下表:
3.函数y=sin x 的图象经变换得到y=A sin (ωx+φ)(A>0,ω>0)
的图象的步骤
【常用结论】
(1)函数 y=A sin (ωx+φ)+k 图象平移的规律:“左加右减,
上加下减”.
(2)函数图象的左右平移本质上是 x 的增减变化.函数图象向左
平移α个单位长度时,只需把函数解析式中的 x 整体代换为 x+α
即可.
(3)函数图象上的点的横坐标的倍数变化本质上是 x 的倍数变
析式中的 x 整体代换为ωx 即可.
考点一 函数 y=A sin (ωx+φ)的图象及变换
答案:C
答案:B
令g(x)=f(x)+x=x-sin x,则g′(x)=1-cos x≥0对任意x∈R
恒成立,可知函数 y=g(x)在 R 上单调递增,且 g(0)=0,
所以函数 y=f(x)+x 的零点个数为 1.故选 B.
答案:B
【题后反思】由函数 y=sin x 的图象通过变换得到 y=Asin(ωx
+φ)的图象有两种途径:“先平移后伸缩”与“先伸缩后平移”.
提醒:三角函数图象左右平移时应注意的问题
①弄清楚平移方向,平移哪个函数的图象,得到哪个函数的
图象.
②注意平移前后两个函数的名称是否一致,若不一致,应先
利用诱导公式化为同名函数.
③由 y=Asin ωx 的图象得到 y=Asin (ωx+φ)的图象时,需平
移 个单位长度,而不是|φ|个单位长度.
考点二 根据函数图象求解析式
[例1](1)已知a是实数,则函数f(x)=1+asin ax的图象不可能
是(
)
A
B
C
D
答案:D
答案:ACD
【题后反思】确定 y=Asin (ωx+φ)+B(A>0,ω>0)的解析
式的步骤
(3)求φ,把图象上一个已知的极值点及其对应的函数值代入求
解;若代入的不是极值点,求解时需注意该点在递增区间上,还
是在递减区间上.
【变式训练】
答案:C
答案:B
考点三 三角函数图象与性质的综合应用
考向 1 函数 y=Asin (ωx+φ)的应用
考向 2 函数零点(方程根)问题
【题后反思】巧用图象解决三角函数相关的方程或不等式
问题
解决与三角函数相关的方程或不等式问题,最基本的方法就
是作出对应函数的图象,然后结合函数图象的特征确定方程的解
或不等式的解集.故准确作出对应函数在指定区间上的图象是解决
问题的关键.
【考法全练】
答案:B
答案:A
⊙三角函数在实际问题中的应用(数学建模)
[例4](2024年辽宁沈阳阶段练习)某游乐场的摩天轮示意图如
图,已知该摩天轮的半径为30 m,轮上最低点与地面的距离为2 m,
沿逆时针方向匀速旋转,旋转一周所需时间为 T=24 min.在圆周
上均匀分布 12 个座舱,标号分别为 1~12(可视为点),在旋转过
程中,座舱与地面的距离 h(单位:m)与时间 t(单位:min)的函数
关系基本符合正弦函数模型,现从图示位置,即 1 号座舱位于圆
周最右端时开始计时,旋转时间为 t min.
(1)求 1 号座舱与地面的距离 h 与时间 t 的函数 h(t)的解析式;
(2)在前 24 min 内,求 1 号座舱与地面的距离为 17 m 时 t 的值.
【高分训练】
阻尼器是一种以提供阻力达到减震效果的专业工程装置.由物
理学知识可知,某阻尼器的运动过程可近似为单摆运动,其离开
平衡位置的位移 y(单位:m)和时间 t(单位:s)的函数关系为 y=
sin (ωt+φ)(ω>0,|φ|<π),如图,若该阻尼器在摆动过程中连续
三次到达同一位置的时间分别为 t1,t2,t3(0<t1<t2<t3),且 t1+
t2=2,t2+t3=5,则在一个周期内阻尼器离开平衡位置的位移大于
0.5 m 的总时间为(
)
1
A. s
3
2
B. s
3
C.1 s
4
D. s
3
答案:C
同课章节目录
