2025秋高考数学复习第三章第一讲弧度制及任意角的三角函数课件(共39张PPT)
文档属性
| 名称 | 2025秋高考数学复习第三章第一讲弧度制及任意角的三角函数课件(共39张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
第三章
三角函数、解三角形
第一讲
弧度制及任意角的三角函数
1.了解任意角的概念和弧度制的概念.
2.能进行弧度与角度的互化.
3.理解任意角三角函数(正弦、余弦、正切)的定义.
1.角的概念的推广
(1)定义:角可以看成平面内一条射线绕着端点从一个位置旋
转到另一个位置所成的图形.
(3)终边相同的角:所有与角α终边相同的角,连同角α在内,
可构成一个集合 S={β|β=α+k·360°,k∈Z}.
2.弧度制的定义和公式
(1)定义:把长度等于半径长的弧所对的圆心角叫做 1 弧度的
角,弧度记作 rad.
(2)公式:
3.任意角的三角函数
(1)定义:设角α终边与单位圆交于 P(x,y),则 sin α=y,
【名师点睛】
(1)三角函数值在各象限的符号规律:一全正,二正弦,三正
切,四余弦.
(3)角度制与弧度制可利用 180°=π rad 进行互化,在同一个
式子中,采用的度量制度必须一致,不可混用.
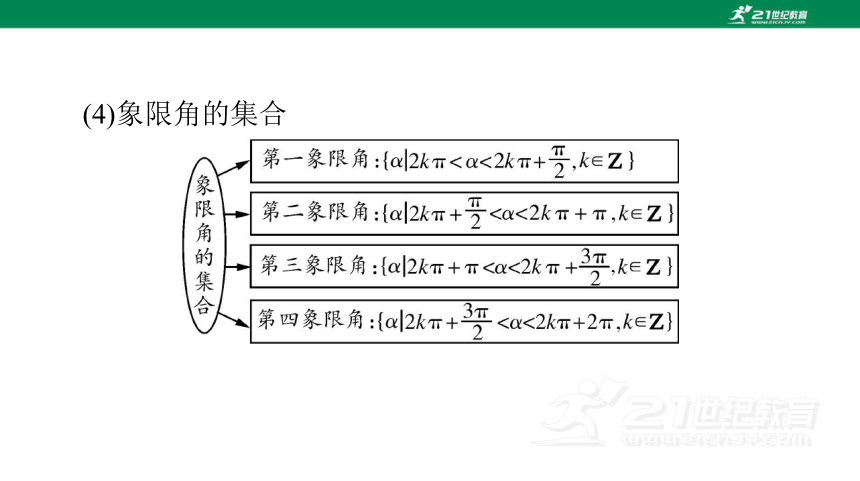
(4)象限角的集合
考点一 角的概念及其集合表示
1.(2023 年上海长宁期末考)与 2 023°终边相同的角是( )
A.-137°
B.227°
C.-227°
D.137°
解析:因为2 023°=-137°+6×360°,故-137°与
2 023°的终边相同.故选 A.
答案:A
答案:B
答案:一或三
【题后反思】(1)利用终边相同的角的集合可以求适合某些条
件的角,方法是先写出与这个角的终边相同的所有角的集合,然
后通过对集合中的参数 k(k∈Z)赋值来求得所需的角.
(2)判断象限角的两种方法
①图象法:在平面直角坐标系中,作出已知角并根据象限角
的定义直接判断已知角是第几象限角;
②转化法:先将已知角化为 k·360°+α(0°≤α<360°,k∈Z)
的形式,即找出与已知角终边相同的角α,再由角α终边所在的象
限判断已知角是第几象限角.
考点二 弧度制及其应用
[例 1](2024 年河北保定阶段练习)(1)已知扇形的圆心角所对的
(2)已知扇形的周长为 40 cm,当它的半径和圆心角取什么值
时,才能使扇形的面积最大?最大面积是多少?
【题后反思】弧度制下有关弧长、扇形面积问题的解题策略
(1)利用扇形的弧长和面积公式解题时,要注意角的单位必须
是弧度.
(2)在解决扇形面积最大值的问题时,常将问题转化为二次函
数的最值问题,利用配方法使问题得到解决.
(3)在解决弧长问题和扇形面积问题时,要合理地利用圆心角
所在的三角形.
【变式训练】
1.莱洛三角形以机械学家莱洛的名字命名,这种图形的应用非
常广泛,不仅用于建筑设计和商品外包装设计,还用于工业生产
中.莱洛三角形的画法如下:先画正三角形,然后分别以
三个顶点为圆心、边长为半径画圆弧得到图形.如图,若
答案:A
答案:B
考点三 三角函数的概念
A.第一象限角
C.第三象限角
B.第二象限角
D.第四象限角
答案:C
(2)(2024 年天津阶段练习)已知角θ的终边经过点 P(3a,-4a),
其中 a≠0.
①求 cos θ的值;
②若θ为第二象限角,求 cos θ+sin θ的值.
【反思感悟】(1)已知角α终边上一点 P 的坐标,可求角α的三
角函数值:先求点 P 到原点的距离,再用三角函数的定义求解.
(2)已知角α的某三角函数值,求角α终边上一点 P 的坐标中的
参数值,可根据定义中的两个量列方程求参数值.
(3)三角函数值的符号及角的终边位置的判断.已知一角的三
角函数值(sin α,cos α,tan α)中任意两个的符号,可分别确定出
角终边所在的可能位置,二者的交集即为该角终边的位置,注意
终边在坐标轴上的特殊情况.
【变式训练】
(多选题)(2024 年内蒙古呼伦贝尔期末考)已知角α的终边经过
点 P(sin 150°,tan 150°),则( )
答案:ABC
⊙三角函数线的应用
[例3](多选题)(2024 年上海模拟)已知 sin α>sin β,那么下列命
题中成立的是(
)
A.若α,β是第一象限角,则 cos α>cos β
B.若α,β是第二象限角,则 tan α>tan β
C.若α,β是第三象限角,则 cos α>cos β
D.若α,β是第四象限角,则 tan α>tan β
解析:设α,β的终边分别交单位圆于 M1,M2 两点,分别过
M1,M2 两点作 x 轴的垂线,垂足为A1,A2,由 sin α>sin β知点M1
的纵坐标大于点 M2 的纵坐标.
对于 A,由题知α,β为第一象限角,如图所示.
由图知|OA1|<|OA2|,即 cos α对于 B,由题知α,β为第二象限角,过点 B(-1,0)作 x 轴的
垂线,分别交 OM1,OM2 的延长线于 B1,B2 两点,如图所示.
由图知|BB1|>|BB2|,即 tan α对于 C,由题知α,β为第三象限角,如图所示.
由图知|OA1|>|OA2|,即 cos α对于 D,由题知α,β为第四象限角,过点 C(1,0)作 x 轴的垂
线,分别交 OM1,OM2 的延长线于 C1,C2 两点,如图所示.
由图知|CC1|<|CC2|,即 tan α>tan β,故 D 正确.故选 D.
答案:D
【反思感悟】利用三角函数线比较大小或解不等式,通常采
用数形结合的方法,一般来说 sin x≥b,cos x≥a,只需作直线
y=b,x=a 与单位圆相交,连接原点与交点即得角的终边所在的
位置,此时再根据方向即可确定相应的 x 的范围.
【高分训练】
1.已知点 P(tan α,cos α)在第三象限,则角α的终边在(
)
A.第一象限
C.第三象限
B.第二象限
D.第四象限
解析:因为 tan α<0,cos α<0,所以α在第二象限.故选 B.
答案:B
第三章
三角函数、解三角形
第一讲
弧度制及任意角的三角函数
1.了解任意角的概念和弧度制的概念.
2.能进行弧度与角度的互化.
3.理解任意角三角函数(正弦、余弦、正切)的定义.
1.角的概念的推广
(1)定义:角可以看成平面内一条射线绕着端点从一个位置旋
转到另一个位置所成的图形.
(3)终边相同的角:所有与角α终边相同的角,连同角α在内,
可构成一个集合 S={β|β=α+k·360°,k∈Z}.
2.弧度制的定义和公式
(1)定义:把长度等于半径长的弧所对的圆心角叫做 1 弧度的
角,弧度记作 rad.
(2)公式:
3.任意角的三角函数
(1)定义:设角α终边与单位圆交于 P(x,y),则 sin α=y,
【名师点睛】
(1)三角函数值在各象限的符号规律:一全正,二正弦,三正
切,四余弦.
(3)角度制与弧度制可利用 180°=π rad 进行互化,在同一个
式子中,采用的度量制度必须一致,不可混用.
(4)象限角的集合
考点一 角的概念及其集合表示
1.(2023 年上海长宁期末考)与 2 023°终边相同的角是( )
A.-137°
B.227°
C.-227°
D.137°
解析:因为2 023°=-137°+6×360°,故-137°与
2 023°的终边相同.故选 A.
答案:A
答案:B
答案:一或三
【题后反思】(1)利用终边相同的角的集合可以求适合某些条
件的角,方法是先写出与这个角的终边相同的所有角的集合,然
后通过对集合中的参数 k(k∈Z)赋值来求得所需的角.
(2)判断象限角的两种方法
①图象法:在平面直角坐标系中,作出已知角并根据象限角
的定义直接判断已知角是第几象限角;
②转化法:先将已知角化为 k·360°+α(0°≤α<360°,k∈Z)
的形式,即找出与已知角终边相同的角α,再由角α终边所在的象
限判断已知角是第几象限角.
考点二 弧度制及其应用
[例 1](2024 年河北保定阶段练习)(1)已知扇形的圆心角所对的
(2)已知扇形的周长为 40 cm,当它的半径和圆心角取什么值
时,才能使扇形的面积最大?最大面积是多少?
【题后反思】弧度制下有关弧长、扇形面积问题的解题策略
(1)利用扇形的弧长和面积公式解题时,要注意角的单位必须
是弧度.
(2)在解决扇形面积最大值的问题时,常将问题转化为二次函
数的最值问题,利用配方法使问题得到解决.
(3)在解决弧长问题和扇形面积问题时,要合理地利用圆心角
所在的三角形.
【变式训练】
1.莱洛三角形以机械学家莱洛的名字命名,这种图形的应用非
常广泛,不仅用于建筑设计和商品外包装设计,还用于工业生产
中.莱洛三角形的画法如下:先画正三角形,然后分别以
三个顶点为圆心、边长为半径画圆弧得到图形.如图,若
答案:A
答案:B
考点三 三角函数的概念
A.第一象限角
C.第三象限角
B.第二象限角
D.第四象限角
答案:C
(2)(2024 年天津阶段练习)已知角θ的终边经过点 P(3a,-4a),
其中 a≠0.
①求 cos θ的值;
②若θ为第二象限角,求 cos θ+sin θ的值.
【反思感悟】(1)已知角α终边上一点 P 的坐标,可求角α的三
角函数值:先求点 P 到原点的距离,再用三角函数的定义求解.
(2)已知角α的某三角函数值,求角α终边上一点 P 的坐标中的
参数值,可根据定义中的两个量列方程求参数值.
(3)三角函数值的符号及角的终边位置的判断.已知一角的三
角函数值(sin α,cos α,tan α)中任意两个的符号,可分别确定出
角终边所在的可能位置,二者的交集即为该角终边的位置,注意
终边在坐标轴上的特殊情况.
【变式训练】
(多选题)(2024 年内蒙古呼伦贝尔期末考)已知角α的终边经过
点 P(sin 150°,tan 150°),则( )
答案:ABC
⊙三角函数线的应用
[例3](多选题)(2024 年上海模拟)已知 sin α>sin β,那么下列命
题中成立的是(
)
A.若α,β是第一象限角,则 cos α>cos β
B.若α,β是第二象限角,则 tan α>tan β
C.若α,β是第三象限角,则 cos α>cos β
D.若α,β是第四象限角,则 tan α>tan β
解析:设α,β的终边分别交单位圆于 M1,M2 两点,分别过
M1,M2 两点作 x 轴的垂线,垂足为A1,A2,由 sin α>sin β知点M1
的纵坐标大于点 M2 的纵坐标.
对于 A,由题知α,β为第一象限角,如图所示.
由图知|OA1|<|OA2|,即 cos α
垂线,分别交 OM1,OM2 的延长线于 B1,B2 两点,如图所示.
由图知|BB1|>|BB2|,即 tan α
由图知|OA1|>|OA2|,即 cos α
线,分别交 OM1,OM2 的延长线于 C1,C2 两点,如图所示.
由图知|CC1|<|CC2|,即 tan α>tan β,故 D 正确.故选 D.
答案:D
【反思感悟】利用三角函数线比较大小或解不等式,通常采
用数形结合的方法,一般来说 sin x≥b,cos x≥a,只需作直线
y=b,x=a 与单位圆相交,连接原点与交点即得角的终边所在的
位置,此时再根据方向即可确定相应的 x 的范围.
【高分训练】
1.已知点 P(tan α,cos α)在第三象限,则角α的终边在(
)
A.第一象限
C.第三象限
B.第二象限
D.第四象限
解析:因为 tan α<0,cos α<0,所以α在第二象限.故选 B.
答案:B
同课章节目录
