2025秋高考数学复习第三章第七讲正弦定理和余弦定理课件(共63张PPT)
文档属性
| 名称 | 2025秋高考数学复习第三章第七讲正弦定理和余弦定理课件(共63张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 10:41:25 | ||
图片预览










文档简介
(共63张PPT)
第七讲 正弦定理和余弦定理
掌握正弦定理、余弦定理,并能解决一些简单的三角形度量
问题.
名称 正弦定理 余弦定理
定理
R是三角形外接圆的半径 a2=b2+c2-2bc cos A;
b2=a2+c2-2ac cos B;
c2=a2+b2-2ab cos C
1.正弦定理与余弦定理
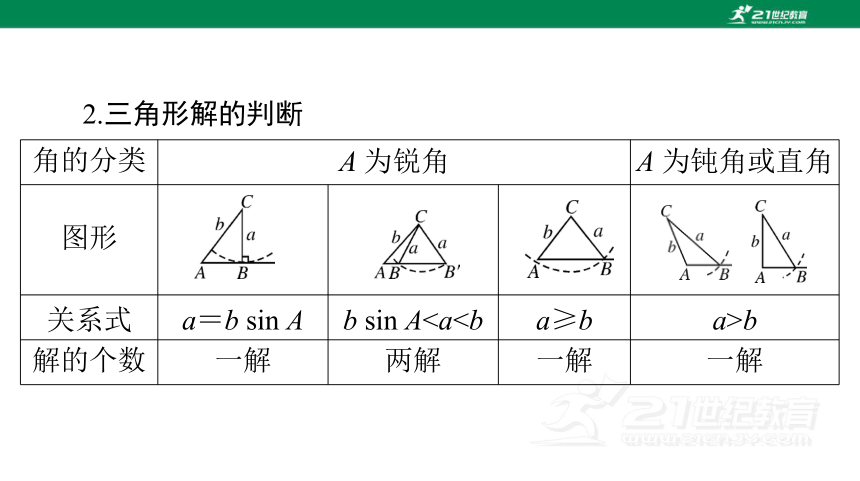
角的分类 A 为锐角 A 为钝角或直角
图形
关系式 a=b sin A b sin Ab
解的个数 一解 两解 一解 一解
2.三角形解的判断
3.三角形中常用的面积公式
【常用结论】
(1)在△ABC 中,A>B a>b sin A>sin B.
(2)三角形中的射影定理
在△ABC 中,a=bcos C+ccos B;
b=acos C+ccos A;
c=bcos A+acos B.
(3)内角和公式的变形
①sin (A+B)=sin C;
②cos (A+B)=-cos C.
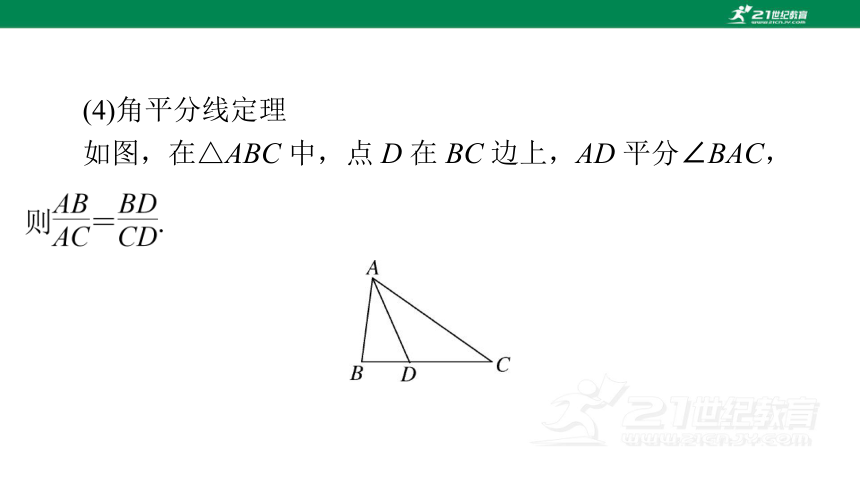
(4)角平分线定理
如图,在△ABC 中,点 D 在 BC 边上,AD 平分∠BAC,
考点一 利用正、余弦定理解三角形
1.(2023 年北京卷)在△ABC 中,(a+c)(sin A-sin C)=b(sin A
-sin B),则 C=(
)
答案:B
2.(多选题)在△ABC 中,根据下列条件解三角形,其中恰有一
解的是(
)
答案:BC
3.(2023 年新课标Ⅰ卷)已知在△ABC 中,A+B=3C,
2sin(A-C)=sin B.
(1)求 sin A 的值;
(2)设 AB=5,求 AB 边上的高.
4.(2024 年天津期末考)在△ABC 中,A,B,C 所对的边分别
(1)求 B 的大小;
(2)求 sin A 的值;
(3)求cos (2A-B)的值.
【题后反思】解三角形问题的技巧
(1)解三角形时,如果式子中含有角的余弦或边的二次式,要
考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则
考虑用正弦定理,以上特征都不明显时,则要考虑两个定理都有
可能用到.
(2)三角形解的个数的判断:已知两角和一边,该三角形是确
定的,其解是唯一的;已知两边和一边的对角,该三角形具有不
唯一性,通常根据三角函数值的有界性和大边对大角定理进行判
断.
考点二 判断三角形的形状
所以 sin Acos B+sin Acos C=sin (A+C)+sin (A+B)=sin Acos C
+cos Asin C+sin Acos B+cos Asin B,得 cos A(sin C+sin B)=0,
因为 00,sin C>0,所以 cos A=0,
0故-1cos (C-A)≤1,要使 cos (A-B)cos (B-C)cos (C-A)=1,则需
cos (A-B)=cos (B-C)=cos (C-A)=1,
所以 A-B=0,B-C=0,C-A=0,
所以A=B=C,△ABC是等边三角形,故D正确.
答案:BCD
(2)(2024 年北京朝阳开学考)已知△ABC 的三个内角 A,B,C
所对的边分别为 a,b,c,则下列条件能推导出△ABC 一定为锐角
三角形的是__________.
对于④,因为 tan(A+B)=
tan A+tan B
=-tan C,则 tan A+
1-tan Atan B
tan B=-tan C+tan Atan Btan C,
故 tan A+tan B+tan C=tan Atan Btan C,
由于 tan A+tan B+tan C>0,
故 tan Atan Btan C>0,
故 A,B,C 均为锐角,△ABC 为锐角三角形,故④正确.
答案:②④
【题后反思】判断三角形形状的常用技巧
若已知条件中既有边又有角,则
(1)化边:通过因式分解、配方等得出边的相应关系,从而判
断三角形的形状.
(2)化角:通过三角恒等变换,得出内角的关系,从而判断三
角形的形状.此时要注意应用 A+B+C=π这个结论.
【变式训练】
A.等腰三角形但一定不是直角三角形
B.等腰直角三角形
C.直角三角形但一定不是等腰三角形
D.等腰三角形或直角三角形
答案:C
考点三 与三角形面积、周长有关的问题
考向 1 与三角形面积有关的问题
【题后反思】(1)求三角形面积的方法
①若已知三角形的一个角(角的大小或该角的正、余弦值)及该
积.
②若已知三角形的三边,可先求其一个角的余弦值,再求其
正弦值,代入①中公式求面积.总之,结合图形选择恰当的面积公
式是解题的关键.
(2)已知三角形面积求边、角的方法
①若求角,就寻求夹这个角的两边的关系,利用面积公式列
方程求解.
②若求边,就寻求与该边(或两边)有关联的角,利用面积公式
列方程求解.
考向 2 与三角形周长有关的问题
答案:12
【考法全练】
(1)求函数 g(x)的解析式;
(2)设锐角三角形 ABC 的内角 A,B,C 所对的边分别为 a,b,
c,若 g(B)=1,且 b=4,求△ABC 面积的最大值.
⊙解平面图形问题
(2)当△BMQ 和△CNQ 的面积相等时,求 tan θ的值.
【反思感悟】平面几何图形中研究或求与角有关的长度、角
度、面积的最值、优化设计等问题,通常是转化到三角形中,利
用正、余弦定理通过运算的方法加以解决.在解决某些具体问题时,
常先引入变量,如边长、角度等,然后把要解三角形的边或角用
所设变量表示出来,再利用正、余弦定理列出方程,解之,若研
究最值,常使用函数思想.
【高分训练】
sin 2A+sin 2B=sin [(A+B)+(A-B)]+sin [(A+B)-(A-B)]
=sin (A+B)cos (A-B)+cos (A+B)sin (A-B)+sin (A+B)cos (A
-B)-cos (A+B)sin (A-B)=2sin (A+B)·cos (A-B)=2sin C·
cos (A-B)=cos (A-B).
第七讲 正弦定理和余弦定理
掌握正弦定理、余弦定理,并能解决一些简单的三角形度量
问题.
名称 正弦定理 余弦定理
定理
R是三角形外接圆的半径 a2=b2+c2-2bc cos A;
b2=a2+c2-2ac cos B;
c2=a2+b2-2ab cos C
1.正弦定理与余弦定理
角的分类 A 为锐角 A 为钝角或直角
图形
关系式 a=b sin A b sin A
解的个数 一解 两解 一解 一解
2.三角形解的判断
3.三角形中常用的面积公式
【常用结论】
(1)在△ABC 中,A>B a>b sin A>sin B.
(2)三角形中的射影定理
在△ABC 中,a=bcos C+ccos B;
b=acos C+ccos A;
c=bcos A+acos B.
(3)内角和公式的变形
①sin (A+B)=sin C;
②cos (A+B)=-cos C.
(4)角平分线定理
如图,在△ABC 中,点 D 在 BC 边上,AD 平分∠BAC,
考点一 利用正、余弦定理解三角形
1.(2023 年北京卷)在△ABC 中,(a+c)(sin A-sin C)=b(sin A
-sin B),则 C=(
)
答案:B
2.(多选题)在△ABC 中,根据下列条件解三角形,其中恰有一
解的是(
)
答案:BC
3.(2023 年新课标Ⅰ卷)已知在△ABC 中,A+B=3C,
2sin(A-C)=sin B.
(1)求 sin A 的值;
(2)设 AB=5,求 AB 边上的高.
4.(2024 年天津期末考)在△ABC 中,A,B,C 所对的边分别
(1)求 B 的大小;
(2)求 sin A 的值;
(3)求cos (2A-B)的值.
【题后反思】解三角形问题的技巧
(1)解三角形时,如果式子中含有角的余弦或边的二次式,要
考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则
考虑用正弦定理,以上特征都不明显时,则要考虑两个定理都有
可能用到.
(2)三角形解的个数的判断:已知两角和一边,该三角形是确
定的,其解是唯一的;已知两边和一边的对角,该三角形具有不
唯一性,通常根据三角函数值的有界性和大边对大角定理进行判
断.
考点二 判断三角形的形状
所以 sin Acos B+sin Acos C=sin (A+C)+sin (A+B)=sin Acos C
+cos Asin C+sin Acos B+cos Asin B,得 cos A(sin C+sin B)=0,
因为 0
0
cos (A-B)=cos (B-C)=cos (C-A)=1,
所以 A-B=0,B-C=0,C-A=0,
所以A=B=C,△ABC是等边三角形,故D正确.
答案:BCD
(2)(2024 年北京朝阳开学考)已知△ABC 的三个内角 A,B,C
所对的边分别为 a,b,c,则下列条件能推导出△ABC 一定为锐角
三角形的是__________.
对于④,因为 tan(A+B)=
tan A+tan B
=-tan C,则 tan A+
1-tan Atan B
tan B=-tan C+tan Atan Btan C,
故 tan A+tan B+tan C=tan Atan Btan C,
由于 tan A+tan B+tan C>0,
故 tan Atan Btan C>0,
故 A,B,C 均为锐角,△ABC 为锐角三角形,故④正确.
答案:②④
【题后反思】判断三角形形状的常用技巧
若已知条件中既有边又有角,则
(1)化边:通过因式分解、配方等得出边的相应关系,从而判
断三角形的形状.
(2)化角:通过三角恒等变换,得出内角的关系,从而判断三
角形的形状.此时要注意应用 A+B+C=π这个结论.
【变式训练】
A.等腰三角形但一定不是直角三角形
B.等腰直角三角形
C.直角三角形但一定不是等腰三角形
D.等腰三角形或直角三角形
答案:C
考点三 与三角形面积、周长有关的问题
考向 1 与三角形面积有关的问题
【题后反思】(1)求三角形面积的方法
①若已知三角形的一个角(角的大小或该角的正、余弦值)及该
积.
②若已知三角形的三边,可先求其一个角的余弦值,再求其
正弦值,代入①中公式求面积.总之,结合图形选择恰当的面积公
式是解题的关键.
(2)已知三角形面积求边、角的方法
①若求角,就寻求夹这个角的两边的关系,利用面积公式列
方程求解.
②若求边,就寻求与该边(或两边)有关联的角,利用面积公式
列方程求解.
考向 2 与三角形周长有关的问题
答案:12
【考法全练】
(1)求函数 g(x)的解析式;
(2)设锐角三角形 ABC 的内角 A,B,C 所对的边分别为 a,b,
c,若 g(B)=1,且 b=4,求△ABC 面积的最大值.
⊙解平面图形问题
(2)当△BMQ 和△CNQ 的面积相等时,求 tan θ的值.
【反思感悟】平面几何图形中研究或求与角有关的长度、角
度、面积的最值、优化设计等问题,通常是转化到三角形中,利
用正、余弦定理通过运算的方法加以解决.在解决某些具体问题时,
常先引入变量,如边长、角度等,然后把要解三角形的边或角用
所设变量表示出来,再利用正、余弦定理列出方程,解之,若研
究最值,常使用函数思想.
【高分训练】
sin 2A+sin 2B=sin [(A+B)+(A-B)]+sin [(A+B)-(A-B)]
=sin (A+B)cos (A-B)+cos (A+B)sin (A-B)+sin (A+B)cos (A
-B)-cos (A+B)sin (A-B)=2sin (A+B)·cos (A-B)=2sin C·
cos (A-B)=cos (A-B).
同课章节目录
