2025秋高考数学复习第七章第四讲直线与圆、圆与圆的位置关系课件(共53张PPT)
文档属性
| 名称 | 2025秋高考数学复习第七章第四讲直线与圆、圆与圆的位置关系课件(共53张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 10:41:58 | ||
图片预览










文档简介
(共53张PPT)
第四讲
直线与圆、圆与圆的位置关系
1.能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置
关系.
2.能用直线和圆的方程解决一些简单的数学问题与实际问题.
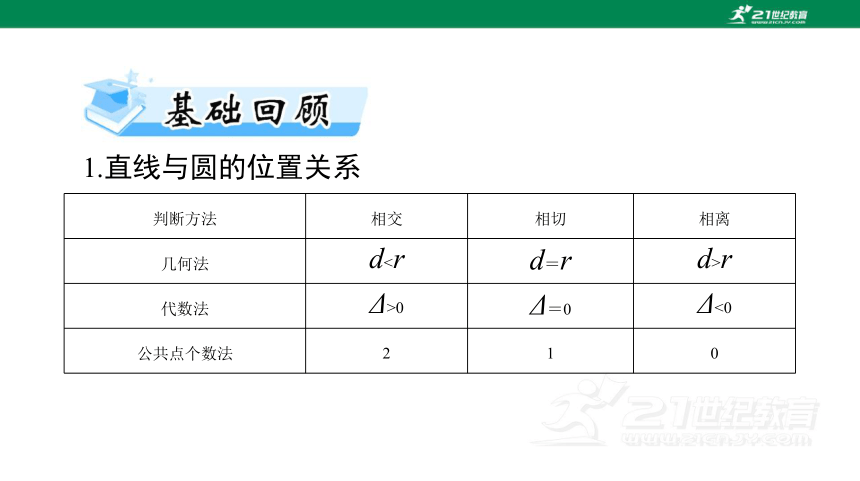
判断方法 相交 相切 相离
几何法 dr
代数法 Δ>0 Δ=0 Δ<0
公共点个数法 2 1 0
1.直线与圆的位置关系
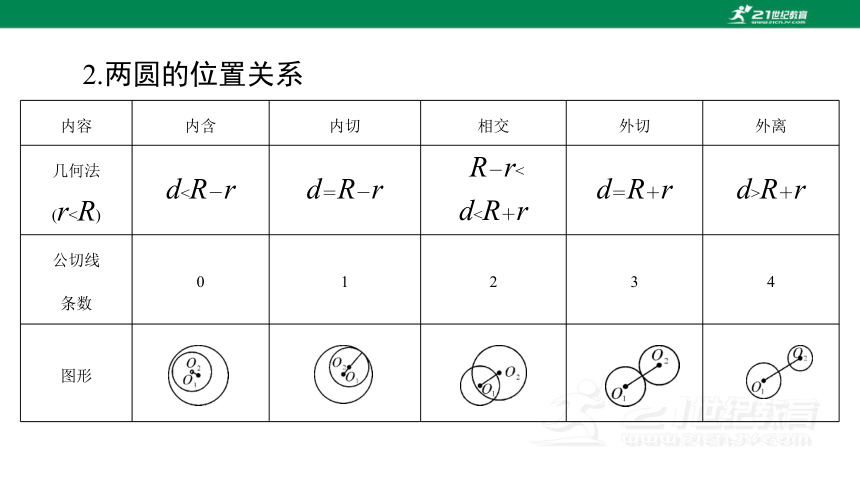
内容 内含 内切 相交 外切 外离
几何法
(rdR+r
公切线
条数 0 1 2 3 4
图形
2.两圆的位置关系
【名师点睛】(1)当两圆相交时,两圆方程(x2,y2 项的系数相
同)相减便可得公共弦所在的直线方程.
(2)直线与圆相交时,圆心到直线的距离 d、半径 r 与弦长 l 满
(3)圆的切线方程常用结论
①过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的圆的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
②过圆(x-a)2+(y-b)2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
考点一 直线与圆的位置关系
[例1](1)直线 l:mx-y+1-m=0 与圆 C:x2+(y-1)2=5 的
)
位置关系是(
A.相交
C.相离
B.相切
D.不确定
答案:A
(2)(2024 年福建福州质检)M(x0,y0)为圆 x2+y2=a2(a>0)内异
)
于圆心的一点,则直线 x0x+y0y=a2 与该圆的位置关系为(
A.相切
B.相交
C.相离
D.相切或相交
答案:C
【题后反思】判断直线与圆的位置关系的常见方法
(1)几何法:利用 d 与 r 的关系判断.
(2)代数法:联立方程之后利用Δ判断.
(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可
判断直线与圆相交.
上述方法中最常用的是几何法,点与圆的位置关系法适用于
动直线问题.
【变式训练】
1.(多选题)已知直线 l:(m+2)x+y-m-3=0 与圆 C:x2+
y2-2x-3=0,则(
)
A.直线 l 过定点(1,1)
B.圆 C 的半径为 4
C.直线 l 与圆 C 一定相交
D.圆心 C 到直线 l 的距离的最大值是 1
解析:直线 l 可化为 m(x-1)+2x+y-3=0,
故直线 l 过定点(1,1),A 正确;
圆 C 的标准方程为(x-1)2+y2=4,故半径为 2,B 错误;
由于定点(1,1)在圆 C 内,故直线 l 与圆 C 一定相交,C正确;
(1,1)到圆心 C(1,0)的距离为 1,故当定点(1,1)与圆心 C
的连线与直线 l 垂直时,距离最大,故圆心 C 到直线 l 的距离的
最大值是 1,D 正确.故选 ACD.
答案:ACD
考点二 圆的切线、弦长问题
考向 1 圆的弦长问题
答案:2
考向 2 圆的切线问题
(1)求过点 P 的圆 C 的切线方程;
(2)求过点 M 的圆 C 的切线方程,并求出切线长.
考向 3 与弦长有关的最值和范围问题
[例4]已知直线 kx-y-k+1=0 与圆(x-1)2+y2=4 相交于 A,
B 两点,则|AB|的最小值为(
)
答案:D
【题后反思】
(1)弦长的两种求法
①几何方法:若弦心距为 d ,圆的半径长为 r ,则弦长 l =
②代数方法:将直线和圆的方程联立方程组,消元后得到一
个一元二次方程.在判别式Δ>0 的前提下,利用根与系数的关系,
根据弦长公式求弦长.
(2)求过某点的圆的切线问题时,应首先确定点与圆的位置关
系,再求切线方程.若点在圆上(即为切点),则过该点的切线只有
一条;若点在圆外,则过该点的切线有两条,此时注意斜率不存
在的切线.
【考法全练】
1.(2023 年新课标Ⅰ卷)过点(0,-2)与圆 x2+y2-4x-1=0 相
切的两条直线的夹角为α,则 sin α=(
)
答案:B
答案:C
解析:过点 C 作 CD⊥l,垂足为 D,连接 CA,CB,如图.
选项 A,圆 C 的标准方程为(x-1)2+(y-2)2=4,则圆心
C(1,2),故 A 正确;
答案:AB
考点三 圆与圆的位置关系
[例 5]已知两圆 x2+y2-2x-6y+1=0,x2+y2-10x-12y+
m=0.
(1)m 取何值时两圆外切?
(2)m 取何值时两圆内切?
(3)当 m=45 时,求两圆的公共弦所在直线的方程和公共弦
的长.
【题后反思】
(1)判断两圆的位置关系时常用几何法,即利用两圆圆心之间
的距离与两圆半径之间的关系,一般不采用代数法.
(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方
程作差消去 x2,y2 项得到.
【变式训练】
答案:C
答案:ABD
答案:[0,3]
⊙阿波罗尼斯圆
公元前 3 世纪,古希腊数学家阿波罗尼斯在《平面轨迹》一
书中,曾研究了众多的平面轨迹问题,其中有如下结果:
到两定点距离之比等于已知数的动点轨迹为直线或圆.如图,
点 A,B 为两定点,动点 P 满足|PA |=λ|PB|.则λ=1 时,动点 P 的
轨迹为直线;当λ>0 且λ≠1 时,动点 P 的轨迹为圆,后世称之为
阿波罗尼斯圆.
证明:设|AB|=2m(m>0),|PA |=λ|PB|,如图,以 AB 的中点
O 为原点,直线 AB 为 x 轴建立平面直角坐标系,
则 A(-m,0),B(m,0).
[例 6]在平面直角坐标系中,A(-2,0),B(2,0),则满足
|PA |=2|PB|的点 P 的轨迹的圆心坐标为________________.
【高分训练】
平面内到两个定点 A,B 的距离之比为定值λ(λ≠1)的点所形成
的图形是圆.人们将这种圆称为阿波罗尼斯圆,简称阿氏圆.已知在
(1)求点 P 的轨迹对应的阿氏圆方程;
(2)求过点 Q(8,-4)且与阿氏圆相切的直线 l 的方程.
第四讲
直线与圆、圆与圆的位置关系
1.能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置
关系.
2.能用直线和圆的方程解决一些简单的数学问题与实际问题.
判断方法 相交 相切 相离
几何法 d
代数法 Δ>0 Δ=0 Δ<0
公共点个数法 2 1 0
1.直线与圆的位置关系
内容 内含 内切 相交 外切 外离
几何法
(r
公切线
条数 0 1 2 3 4
图形
2.两圆的位置关系
【名师点睛】(1)当两圆相交时,两圆方程(x2,y2 项的系数相
同)相减便可得公共弦所在的直线方程.
(2)直线与圆相交时,圆心到直线的距离 d、半径 r 与弦长 l 满
(3)圆的切线方程常用结论
①过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的圆的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
②过圆(x-a)2+(y-b)2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
考点一 直线与圆的位置关系
[例1](1)直线 l:mx-y+1-m=0 与圆 C:x2+(y-1)2=5 的
)
位置关系是(
A.相交
C.相离
B.相切
D.不确定
答案:A
(2)(2024 年福建福州质检)M(x0,y0)为圆 x2+y2=a2(a>0)内异
)
于圆心的一点,则直线 x0x+y0y=a2 与该圆的位置关系为(
A.相切
B.相交
C.相离
D.相切或相交
答案:C
【题后反思】判断直线与圆的位置关系的常见方法
(1)几何法:利用 d 与 r 的关系判断.
(2)代数法:联立方程之后利用Δ判断.
(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可
判断直线与圆相交.
上述方法中最常用的是几何法,点与圆的位置关系法适用于
动直线问题.
【变式训练】
1.(多选题)已知直线 l:(m+2)x+y-m-3=0 与圆 C:x2+
y2-2x-3=0,则(
)
A.直线 l 过定点(1,1)
B.圆 C 的半径为 4
C.直线 l 与圆 C 一定相交
D.圆心 C 到直线 l 的距离的最大值是 1
解析:直线 l 可化为 m(x-1)+2x+y-3=0,
故直线 l 过定点(1,1),A 正确;
圆 C 的标准方程为(x-1)2+y2=4,故半径为 2,B 错误;
由于定点(1,1)在圆 C 内,故直线 l 与圆 C 一定相交,C正确;
(1,1)到圆心 C(1,0)的距离为 1,故当定点(1,1)与圆心 C
的连线与直线 l 垂直时,距离最大,故圆心 C 到直线 l 的距离的
最大值是 1,D 正确.故选 ACD.
答案:ACD
考点二 圆的切线、弦长问题
考向 1 圆的弦长问题
答案:2
考向 2 圆的切线问题
(1)求过点 P 的圆 C 的切线方程;
(2)求过点 M 的圆 C 的切线方程,并求出切线长.
考向 3 与弦长有关的最值和范围问题
[例4]已知直线 kx-y-k+1=0 与圆(x-1)2+y2=4 相交于 A,
B 两点,则|AB|的最小值为(
)
答案:D
【题后反思】
(1)弦长的两种求法
①几何方法:若弦心距为 d ,圆的半径长为 r ,则弦长 l =
②代数方法:将直线和圆的方程联立方程组,消元后得到一
个一元二次方程.在判别式Δ>0 的前提下,利用根与系数的关系,
根据弦长公式求弦长.
(2)求过某点的圆的切线问题时,应首先确定点与圆的位置关
系,再求切线方程.若点在圆上(即为切点),则过该点的切线只有
一条;若点在圆外,则过该点的切线有两条,此时注意斜率不存
在的切线.
【考法全练】
1.(2023 年新课标Ⅰ卷)过点(0,-2)与圆 x2+y2-4x-1=0 相
切的两条直线的夹角为α,则 sin α=(
)
答案:B
答案:C
解析:过点 C 作 CD⊥l,垂足为 D,连接 CA,CB,如图.
选项 A,圆 C 的标准方程为(x-1)2+(y-2)2=4,则圆心
C(1,2),故 A 正确;
答案:AB
考点三 圆与圆的位置关系
[例 5]已知两圆 x2+y2-2x-6y+1=0,x2+y2-10x-12y+
m=0.
(1)m 取何值时两圆外切?
(2)m 取何值时两圆内切?
(3)当 m=45 时,求两圆的公共弦所在直线的方程和公共弦
的长.
【题后反思】
(1)判断两圆的位置关系时常用几何法,即利用两圆圆心之间
的距离与两圆半径之间的关系,一般不采用代数法.
(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方
程作差消去 x2,y2 项得到.
【变式训练】
答案:C
答案:ABD
答案:[0,3]
⊙阿波罗尼斯圆
公元前 3 世纪,古希腊数学家阿波罗尼斯在《平面轨迹》一
书中,曾研究了众多的平面轨迹问题,其中有如下结果:
到两定点距离之比等于已知数的动点轨迹为直线或圆.如图,
点 A,B 为两定点,动点 P 满足|PA |=λ|PB|.则λ=1 时,动点 P 的
轨迹为直线;当λ>0 且λ≠1 时,动点 P 的轨迹为圆,后世称之为
阿波罗尼斯圆.
证明:设|AB|=2m(m>0),|PA |=λ|PB|,如图,以 AB 的中点
O 为原点,直线 AB 为 x 轴建立平面直角坐标系,
则 A(-m,0),B(m,0).
[例 6]在平面直角坐标系中,A(-2,0),B(2,0),则满足
|PA |=2|PB|的点 P 的轨迹的圆心坐标为________________.
【高分训练】
平面内到两个定点 A,B 的距离之比为定值λ(λ≠1)的点所形成
的图形是圆.人们将这种圆称为阿波罗尼斯圆,简称阿氏圆.已知在
(1)求点 P 的轨迹对应的阿氏圆方程;
(2)求过点 Q(8,-4)且与阿氏圆相切的直线 l 的方程.
同课章节目录
