2025秋高考数学复习第七章第八讲直线与圆锥曲线课件(共43张PPT)
文档属性
| 名称 | 2025秋高考数学复习第七章第八讲直线与圆锥曲线课件(共43张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 10:42:15 | ||
图片预览











文档简介
(共43张PPT)
第八讲 直线与圆锥曲线
1.了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和
解决实际问题中的作用.
2.能用坐标法解决一些与圆锥曲线有关的简单几何问题(直线
与圆锥曲线的位置关系)和实际问题.
3.通过圆锥曲线与方程的学习,进一步体会数形结合的思想.
直线与圆锥曲线的位置关系的判定
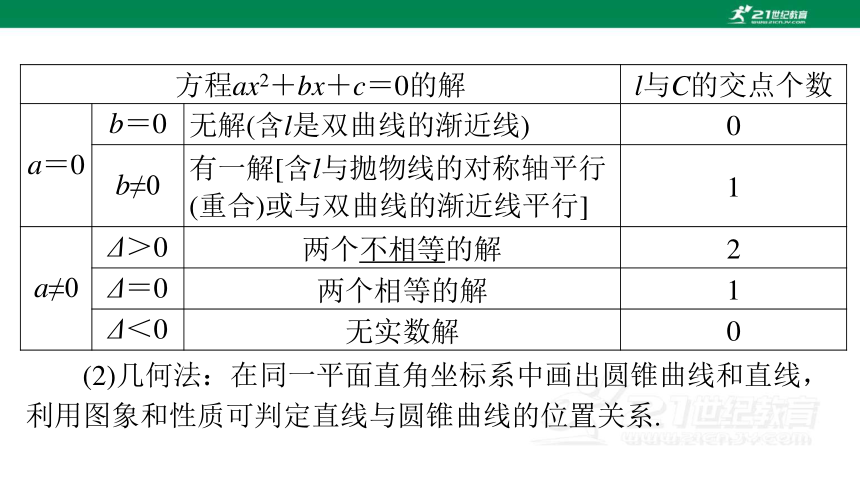
(1)代数法:把圆锥曲线方程 C 与直线方程 l 联立消去 y,整理
得到关于 x 的方程 ax2+bx+c=0.
方程ax2+bx+c=0的解 l与C的交点个数
a=0 b=0 无解(含l是双曲线的渐近线) 0
b≠0 有一解[含l与抛物线的对称轴平行
(重合)或与双曲线的渐近线平行] 1
a≠0 Δ>0 两个不相等的解 2
Δ=0 两个相等的解 1
Δ<0 无实数解 0
(2)几何法:在同一平面直角坐标系中画出圆锥曲线和直线,
利用图象和性质可判定直线与圆锥曲线的位置关系.
【名师点睛】
(1)直线与双曲线交于一点时,易误认为只有直线与双曲线相
切.而当直线与双曲线的渐近线平行时,直线与双曲线相交于一点.
(2)直线与抛物线交于一点时,除直线与抛物线相切外,易忽
视直线与抛物线的对称轴平行或重合时也与抛物线相交于一点.
(3)直线与圆锥曲线的相交弦长问题
设斜率为 k(k≠0)的直线 l 与圆锥曲线 C 相交于 M,N 两点,
M(x1,y1),N(x2,y2),则
(4)解决直线与圆锥曲线的位置关系问题的规律
“联立方程求交点,根与系数的关系求弦长,根的分布找范
围,曲线定义不能忘.”
考点一 直线和圆锥曲线的位置关系
答案:A
答案:B
答案:A
【题后反思】过椭圆或双曲线上一点的切线方程
考点二 弦长问题
(1)求椭圆的方程;
【题后反思】
(1)弦长的求解方法
①当弦的两端点坐标易求时,可直接利用两点间的距离公式
求解.
②当直线的斜率存在时,斜率为 k(k≠0)的直线 l 与椭圆相交
于A(x1,y1),B(x2,y2)两个不同的点,则弦长公式的常见形式有
如下两种:
【变式训练】
答案:B
考点三 中点弦问题
考向 1 由中点弦确定直线方程
答案:D
考向 2 由中点弦确定曲线方程或参数的值
答案:D
答案:C
【题后反思】(1)处理中点弦问题常用的方法
【考法全练】
答案:C
答案:A
第八讲 直线与圆锥曲线
1.了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和
解决实际问题中的作用.
2.能用坐标法解决一些与圆锥曲线有关的简单几何问题(直线
与圆锥曲线的位置关系)和实际问题.
3.通过圆锥曲线与方程的学习,进一步体会数形结合的思想.
直线与圆锥曲线的位置关系的判定
(1)代数法:把圆锥曲线方程 C 与直线方程 l 联立消去 y,整理
得到关于 x 的方程 ax2+bx+c=0.
方程ax2+bx+c=0的解 l与C的交点个数
a=0 b=0 无解(含l是双曲线的渐近线) 0
b≠0 有一解[含l与抛物线的对称轴平行
(重合)或与双曲线的渐近线平行] 1
a≠0 Δ>0 两个不相等的解 2
Δ=0 两个相等的解 1
Δ<0 无实数解 0
(2)几何法:在同一平面直角坐标系中画出圆锥曲线和直线,
利用图象和性质可判定直线与圆锥曲线的位置关系.
【名师点睛】
(1)直线与双曲线交于一点时,易误认为只有直线与双曲线相
切.而当直线与双曲线的渐近线平行时,直线与双曲线相交于一点.
(2)直线与抛物线交于一点时,除直线与抛物线相切外,易忽
视直线与抛物线的对称轴平行或重合时也与抛物线相交于一点.
(3)直线与圆锥曲线的相交弦长问题
设斜率为 k(k≠0)的直线 l 与圆锥曲线 C 相交于 M,N 两点,
M(x1,y1),N(x2,y2),则
(4)解决直线与圆锥曲线的位置关系问题的规律
“联立方程求交点,根与系数的关系求弦长,根的分布找范
围,曲线定义不能忘.”
考点一 直线和圆锥曲线的位置关系
答案:A
答案:B
答案:A
【题后反思】过椭圆或双曲线上一点的切线方程
考点二 弦长问题
(1)求椭圆的方程;
【题后反思】
(1)弦长的求解方法
①当弦的两端点坐标易求时,可直接利用两点间的距离公式
求解.
②当直线的斜率存在时,斜率为 k(k≠0)的直线 l 与椭圆相交
于A(x1,y1),B(x2,y2)两个不同的点,则弦长公式的常见形式有
如下两种:
【变式训练】
答案:B
考点三 中点弦问题
考向 1 由中点弦确定直线方程
答案:D
考向 2 由中点弦确定曲线方程或参数的值
答案:D
答案:C
【题后反思】(1)处理中点弦问题常用的方法
【考法全练】
答案:C
答案:A
同课章节目录
