2025秋高考数学复习第七章第六讲双曲线课件(共48张PPT)
文档属性
| 名称 | 2025秋高考数学复习第七章第六讲双曲线课件(共48张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 10:42:56 | ||
图片预览











文档简介
(共48张PPT)
第六讲 双曲线
1.了解双曲线的定义、几何图形和标准方程,以及他的简单
几何性质.
2.通过圆锥曲线与方程的学习,进一步体会数形结合的思想.
1.双曲线的概念
平面内与两个定点 F1,F2 的距离的差的绝对值等于非零常数
(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦
点,两焦点间的距离叫做双曲线的焦距.
集合 P={M|||MF1|-|MF2||=2a,0<2a<|F1F2|},|F1F2|=2c,
其中 a,c 为常数且 a>0,c>0.
(1)当 a(2)当 a=c 时,点 M 的轨迹是两条射线;
(3)当 a>c 时,点 M 不存在.
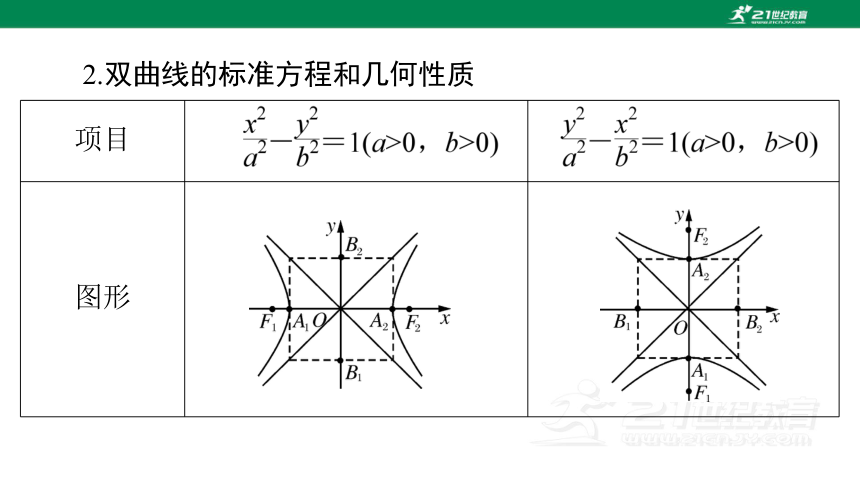
项目
图形
2.双曲线的标准方程和几何性质
项目
性
质 范围 x≥a或x≤-a,y∈R x∈R,y≤-a或y≥a
对称性 对称轴:坐标轴 对称中心:原点
顶点 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
渐近线
项目
性
质 离心率
实、虚轴 实轴A1A2的长为2a;虚轴B1B2的长为2b
a,b,c
的关系 c2=a2+b2(c>a>0,c>b>0)
3.等轴双曲线
实轴和虚轴等长的双曲线叫做等轴双曲线,其渐近线方程为
y=±x,离心率为
【名师点睛】双曲线中的几个常用结论
(1)焦点到渐近线的距离为 b.设渐近线与实轴的夹角为θ,则双
曲线的离心率
考点一 双曲线的定义
答案:C
2.已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆
M 与圆 C1 及圆 C2 均外切,则点 M 的轨迹方程为_____________.
解析:如图所示,设动圆 M 与圆 C1 和圆 C2 分别外切于 A,
B 两点.
根据两圆外切的条件,得|MC1|-|AC1|=|MA|,|MC2|-|BC2|=
|MB|.
答案:4 或 12
【题后反思】(1)利用双曲线的定义判定平面内动点的轨迹是
否为双曲线,进而根据要求可求出双曲线方程.
(2)在“焦点三角形”中,常利用正弦定理、余弦定理,经常
结合||PF1|-|PF2||=2a,运用平方的方法,建立与|PF1|·|PF2|的联系.
考点二 双曲线的标准方程
答案:D
解析:由题知点 P 在第四象限,PF1⊥PF2,如图.
答案:A
考点三 双曲线的几何性质
考向 1 求双曲线的渐近线方程
答案:C
答案:C
考向 2 双曲线的离心率
通性通法:求双曲线的离心率或其范围的方法
答案:A
【考法全练】
1.(2024 年全国甲卷理科)已知双曲线的两个焦点分别为(0,4),
(0,-4),点(-6,4)在该双曲线上,则该双曲线的离心率为(
)
答案:C
答案:y=±x
⊙与双曲线有关的最值和范围问题
答案:A
【题后反思】与双曲线有关的取值范围问题的解题思路
(1)若条件中存在不等关系,则借助此关系直接变换求解.
(2)若条件中没有不等关系,要善于发现隐含的不等关系或借
助曲线中不等关系来解决.
【高分训练】
答案:D
答案:(0,2)
第六讲 双曲线
1.了解双曲线的定义、几何图形和标准方程,以及他的简单
几何性质.
2.通过圆锥曲线与方程的学习,进一步体会数形结合的思想.
1.双曲线的概念
平面内与两个定点 F1,F2 的距离的差的绝对值等于非零常数
(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦
点,两焦点间的距离叫做双曲线的焦距.
集合 P={M|||MF1|-|MF2||=2a,0<2a<|F1F2|},|F1F2|=2c,
其中 a,c 为常数且 a>0,c>0.
(1)当 a
(3)当 a>c 时,点 M 不存在.
项目
图形
2.双曲线的标准方程和几何性质
项目
性
质 范围 x≥a或x≤-a,y∈R x∈R,y≤-a或y≥a
对称性 对称轴:坐标轴 对称中心:原点
顶点 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
渐近线
项目
性
质 离心率
实、虚轴 实轴A1A2的长为2a;虚轴B1B2的长为2b
a,b,c
的关系 c2=a2+b2(c>a>0,c>b>0)
3.等轴双曲线
实轴和虚轴等长的双曲线叫做等轴双曲线,其渐近线方程为
y=±x,离心率为
【名师点睛】双曲线中的几个常用结论
(1)焦点到渐近线的距离为 b.设渐近线与实轴的夹角为θ,则双
曲线的离心率
考点一 双曲线的定义
答案:C
2.已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆
M 与圆 C1 及圆 C2 均外切,则点 M 的轨迹方程为_____________.
解析:如图所示,设动圆 M 与圆 C1 和圆 C2 分别外切于 A,
B 两点.
根据两圆外切的条件,得|MC1|-|AC1|=|MA|,|MC2|-|BC2|=
|MB|.
答案:4 或 12
【题后反思】(1)利用双曲线的定义判定平面内动点的轨迹是
否为双曲线,进而根据要求可求出双曲线方程.
(2)在“焦点三角形”中,常利用正弦定理、余弦定理,经常
结合||PF1|-|PF2||=2a,运用平方的方法,建立与|PF1|·|PF2|的联系.
考点二 双曲线的标准方程
答案:D
解析:由题知点 P 在第四象限,PF1⊥PF2,如图.
答案:A
考点三 双曲线的几何性质
考向 1 求双曲线的渐近线方程
答案:C
答案:C
考向 2 双曲线的离心率
通性通法:求双曲线的离心率或其范围的方法
答案:A
【考法全练】
1.(2024 年全国甲卷理科)已知双曲线的两个焦点分别为(0,4),
(0,-4),点(-6,4)在该双曲线上,则该双曲线的离心率为(
)
答案:C
答案:y=±x
⊙与双曲线有关的最值和范围问题
答案:A
【题后反思】与双曲线有关的取值范围问题的解题思路
(1)若条件中存在不等关系,则借助此关系直接变换求解.
(2)若条件中没有不等关系,要善于发现隐含的不等关系或借
助曲线中不等关系来解决.
【高分训练】
答案:D
答案:(0,2)
同课章节目录
