2025秋高考数学复习第一章第一讲集合课件(共44张PPT)
文档属性
| 名称 | 2025秋高考数学复习第一章第一讲集合课件(共44张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 972.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 10:49:11 | ||
图片预览











文档简介
(共44张PPT)
第一章
集合与常用逻辑用语、不等式
第一讲 集合
1.了解集合的含义,体会元素与集合的属于关系;能用自然语
言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
2.理解集合之间包含与相等的含义,能识别给定集合的子集;
在具体情境中,了解全集与空集的含义.
3.(1)理解两个集合的并集与交集的含义,会求两个简单集合
的并集与交集.
(2)理解在给定集合中一个子集的补集的含义,会求给定子集
的补集.
(3)能使用 Venn 图表达集合间的基本关系及集合的基本运算.
1.元素与集合
(1)集合中元素的三个特性:确定性、互异性、无序性.
(2)元素与集合的关系是属于(∈)或不属于( ).
(3)集合的三种表示方法:列举法、描述法、图示法.
集合 非负整数集
(或自然数集) 正整数集 整数集 有理数集 实数集
符号 N N*(或N+) Z Q R
(4)常见数集的记法
2.集合间的基本关系
(1)子集:若对任意 x∈A,都有 x∈B,则 A B 或 B A.
(2)真子集:若 A B,且集合 B 中至少有一个元素不属于集合
A,则 A
B 或 B A.
(3)相等:若 A B,且 B A,则 A=B.
(4)空集的性质: 是任何集合的子集,是任何非空集合的真子
集.
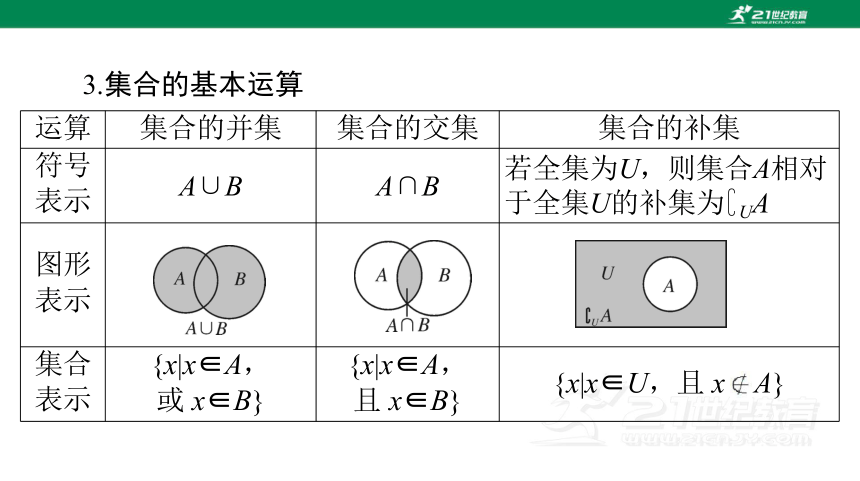
运算 集合的并集 集合的交集 集合的补集
符号
表示 A∪B A∩B 若全集为U,则集合A相对于全集U的补集为 UA
图形
表示
集合
表示 {x|x∈A,
或 x∈B} {x|x∈A,
且 x∈B} {x|x∈U,且 x A}
3.集合的基本运算
4.集合的运算性质
(1)A∩A=A,A∩ = ,A∩B=B∩A.
(2)A∪A=A,A∪ =A,A∪B=B∪A.
(3)A∩( UA)= ,A∪( UA)=U, U( UA)=A.
【名师点睛】
(1)若有限集A中有n个元素,则A的子集有2n个,真子集有(2n-1)个.
(2)子集的传递性:A B,B C A C.
(3)A B A∩B=A A∪B=B UA UB.
(4) U(A∩B)=( UA)∪( UB), U(A∪B)=( UA)∩( UB).
【易错警示】
(1)运用数轴图示法要注意端点是实心还是空心.
(2)在解决含参数的集合问题时,要注意检验集合中元素的互
异性,否则很可能会因为不满足“互异性”而导致解题错误.
考点一 集合的概念
1.(2024 年河北石家庄模拟)已知集合 M={x|x=2k,k∈Z},
Q={x|x=2k+1,k∈Z},P={x|x=4k+1,k∈Z},若 m∈P,
n∈Q,则( )
A.m+n∈M
C.m+n∈P
B.m+n∈Q
D.m+n 不属于 M,Q,P 中的任意一个
解析:∵m∈P,n∈Q,
∴m=4k1+1,k1∈Z,n=2k2+1,k2∈Z,
∴m+n=4k1+1+2k2+1=2(2k1+k2+1),2k1+k2+1∈Z,
∴m+n∈M.故选 A.
答案:A
2.下列关于 0 与 说法不正确的是(
)
A.0
C.{0}=
B.0∈{0}
D.{0}
解析:因为 是不含任何元素的集合,故 A 正确,C 不正确;
对于选项 B,0∈{0},故 B 正确;对于选项 D,因为 是任何集合
的子集,所以{0} ,故 D 正确.故选 C.
答案:C
3.(2024 年四川期中考)已知集合 A={x|x2+ax+6<0},若1 A,
)
则 a 的取值范围为(
A.[-7,+∞)
C.(-∞,-7]
B.(-7,+∞)
D.(-∞,-7)
解析:由 1 A,可得12+a×1+6≥0,解得a≥-7,即a的
取值范围为[-7,+∞).故选 A.
答案:A
【题后反思】解决集合概念问题的关键有三点:一是确定构
成集合的元素;二是确定元素的限制条件;三是根据元素的特征
(满足的条件)构造关系式解决相应问题.
考点二 集合间的基本关系
则(
)
A.M N
B.N M
C.M=N
D.M∩N=
答案:B
(2)(2024 年广西北海期中考)已知集合 M 满足{-1,1} M
{-4,-1,1,2},则不同的 M 的个数为(
)
A.8
B.6
C.4
D.2
解析:由{-1,1} M {-4,-1,1,2}可知 M 可以是
{- 1,1},{-1,1,2},{-1,1,-4},{-1,1,2,-4},
故不同的 M 的个数为 4.
答案:C
(3)已知集合A={x|-3≤x≤4},B={x|2m-1≤x≤m+1},且
B A,则实数 m 的取值范围是________.
解析:∵B A,
①当 B= 时,2m-1>m+1,解得 m>2;
综上所述,实数 m 的取值范围是[-1,+∞).
答案:[-1,+∞)
【题后反思】判断集合间基本关系的方法
(1)列举法:用列举法表示集合,再从元素中寻求关系.
(2)化简集合法:用描述法表示的集合,若代表元素的表达式
比较复杂,往往需化简表达式,再寻求两个集合的关系.
特别提醒:在涉及集合关系时,必须优先考虑空集的情况,
否则会造成漏解.
【变式训练】
1.(2024 年天津期中考)若集合 A={2,3,4,5,6},则 A 的
真子集的个数为(
)
A.32
B.31
C.25
D.24
解析:集合 A={2,3,4,5,6}共有 5 个元素,所以集合 A
共有 25-1=31 个真子集.故选 B.
答案:B
2.(2023 年新课标Ⅱ卷)设集合 A={0,-a},B={1,a-2,
2a-2},若 A B,则 a=(
)
A.2
B.1
2
C.
3
D.-1
解析:依题意,a-2=0 或 2a-2=0,当 a-2=0 时,解得
a=2,此时 A={0,-2},B={1,0,2},不符合题意;当 2a-
2=0 时,解得 a=1,此时 A={0,-1},B={1,-1,0},符合
题意.故选 B.
答案:B
3.(2024 年陕西阶段练习)已知集合 A={1,2,3,4},B=
{x|-1≤x≤3},则 A∩B=(
A.{1,2}
C.{0,1,2}
)
B.{1,2,3}
D.{0,1,2,3}
解析:A={1,2,3,4},B={x|-1≤x≤3},则 A∩B={1,
2,3}.故选 B.
答案:B
考点三 集合的基本运算及运算性质
考向 1 集合的基本运算
通性通法:(1)一般来讲,集合中的元素若是离散的,可用
Venn图表示;数集中的元素若是连续的,则可用数轴表示,此时
要注意端点的情况.
(2)运算过程中要注意集合间的特殊关系的使用,灵活使用这
些关系,会使运算简化.
[例2](1)(2023 年湖北月考)已知全集 U=A∪B={x∈N|0<x+
1<6},A={1,2},若 A∩B= ,则 B=(
)
A.{0,3,4}
C.{-1,0}
B.{0,1}
D.{2,3,4}
解析:由题意,可得 U={x∈N|0<x+1<6}={0,1,2,3,
4},因为 U=A∪B,A∩B= ,A={1,2},所以 B={0,3,4}.
故选 A.
答案:A
(2)(2024 年山东阶段练习)设全集 U=R,A={x|-3≤x<4},
A.{x|x≤-2}
C.{x|x≥4}
B.{x|x>-2}
D.{x|x≤4}
又 A={x|-3≤x<4},所以 A∩B={x|-2≤x<4},所以图中阴
影部分表示的集合为 B(A∩B)={x|x≥4}.
答案:C
考向 2 利用集合的基本运算求参数
通性通法:利用集合的基本运算求参数的值或取值范围的
方法
(1)若集合中的元素能一一列举,则一般先用观察法得到不同
集合中元素之间的关系,再列方程(组)求解.
(2)与不等式有关的集合,一般利用数轴解决,要注意端点值
能否取到.
提醒:在求出参数后,注意结果的验证(满足互异性).
[例3](1)(2023 年河北衡水模拟) 已知集合 A ={x|y=ln (1-
x2)},B={x|x≤a},若( RA)∪B=R,则实数a的取值范围为( )
A.(1,+∞)
C.(-∞,1)
B.[1,+∞)
D.(-∞,1]
解析:由题可知A={x|y=ln (1-x2)}={x|-1{x|x≤-1或x≥1},所以由( RA)∪B=R,得a≥1.
答案:B
(2)已知集合A={x|x2+x-6=0},B={x|mx+1=0},且A∩B
=B,则实数 m 的取值集合是________________.
解析:A={x|x2+x-6=0}={-3,2},
由 A∩B=B,知 B A.
当 B= 时,m=0,满足题意;
【考法全练】
1.(2024年四川期中考)已知集合A={x|-2≤x≤10},B= {x|1-m≤x≤1+m}.若B∩ RA= ,则实数m的取值范围为( )
A.0≤m≤3
B.0≤m≤9
C.m≥3或m≤9
D.3≤m≤9
答案:A
2.(多选题)已知全集U=Z,集合A={x|2x+1≥0,x∈Z},
B={-1,0,1,2},则( )
A.A∩B={0,1,2}
B.A∪B={x|x≥0}
C.( UA)∩B={-1}
D.A∩B的真子集个数是7
答案:ACD
3.(多选题)(2023 年湖南衡阳期末考)能正确表示图中阴影部分
的是(
)
A.B∩( UA) B.A∩( UB) C. (A∪B)A D. B(A∩B)
解析:因为阴影部分在 B 中不在 A 中,根据集合的运算分析
可知 ACD 正确.
答案:ACD
答案:AD
⊙集合的新定义问题的理解
“新定义”主要是指定义新概念、新公式、新定理、新法则、
新运算五种,然后根据此新定义去解决问题,有时还需要用类比
的方法去理解新定义.
答案:AC
【高分训练】
1.(2023 年云南保山模拟)定义集合运算:A+B={z|z=x+y,
x∈A,y∈B},设 A={1,2},B={1,2,3},则集合 A+B 的所
有元素之和为(
)
A.14
B.15
C.16
D.18
解析:由题设知 A+B={2,3,4,5},∴所有元素之和为 2
+3+4+5=14.故选 A.
答案:A
2.(2024 年天津阶段练习)设 M,P 是两个非空集合,规定 M-
)
P={x|x∈M 且 x P},根据这一规定,M-(M-P)等于(
A.M
B.P
C.M∪P
D.M∩P
解析:M-(M-P)={x|x∈M,且 x (M-P)},
用 venn 图表示集合 M,P 的关系如下图.
阴影部分为 M-P,所以 M-(M-P)=M∩P.故选 D.
答案:D
第一章
集合与常用逻辑用语、不等式
第一讲 集合
1.了解集合的含义,体会元素与集合的属于关系;能用自然语
言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
2.理解集合之间包含与相等的含义,能识别给定集合的子集;
在具体情境中,了解全集与空集的含义.
3.(1)理解两个集合的并集与交集的含义,会求两个简单集合
的并集与交集.
(2)理解在给定集合中一个子集的补集的含义,会求给定子集
的补集.
(3)能使用 Venn 图表达集合间的基本关系及集合的基本运算.
1.元素与集合
(1)集合中元素的三个特性:确定性、互异性、无序性.
(2)元素与集合的关系是属于(∈)或不属于( ).
(3)集合的三种表示方法:列举法、描述法、图示法.
集合 非负整数集
(或自然数集) 正整数集 整数集 有理数集 实数集
符号 N N*(或N+) Z Q R
(4)常见数集的记法
2.集合间的基本关系
(1)子集:若对任意 x∈A,都有 x∈B,则 A B 或 B A.
(2)真子集:若 A B,且集合 B 中至少有一个元素不属于集合
A,则 A
B 或 B A.
(3)相等:若 A B,且 B A,则 A=B.
(4)空集的性质: 是任何集合的子集,是任何非空集合的真子
集.
运算 集合的并集 集合的交集 集合的补集
符号
表示 A∪B A∩B 若全集为U,则集合A相对于全集U的补集为 UA
图形
表示
集合
表示 {x|x∈A,
或 x∈B} {x|x∈A,
且 x∈B} {x|x∈U,且 x A}
3.集合的基本运算
4.集合的运算性质
(1)A∩A=A,A∩ = ,A∩B=B∩A.
(2)A∪A=A,A∪ =A,A∪B=B∪A.
(3)A∩( UA)= ,A∪( UA)=U, U( UA)=A.
【名师点睛】
(1)若有限集A中有n个元素,则A的子集有2n个,真子集有(2n-1)个.
(2)子集的传递性:A B,B C A C.
(3)A B A∩B=A A∪B=B UA UB.
(4) U(A∩B)=( UA)∪( UB), U(A∪B)=( UA)∩( UB).
【易错警示】
(1)运用数轴图示法要注意端点是实心还是空心.
(2)在解决含参数的集合问题时,要注意检验集合中元素的互
异性,否则很可能会因为不满足“互异性”而导致解题错误.
考点一 集合的概念
1.(2024 年河北石家庄模拟)已知集合 M={x|x=2k,k∈Z},
Q={x|x=2k+1,k∈Z},P={x|x=4k+1,k∈Z},若 m∈P,
n∈Q,则( )
A.m+n∈M
C.m+n∈P
B.m+n∈Q
D.m+n 不属于 M,Q,P 中的任意一个
解析:∵m∈P,n∈Q,
∴m=4k1+1,k1∈Z,n=2k2+1,k2∈Z,
∴m+n=4k1+1+2k2+1=2(2k1+k2+1),2k1+k2+1∈Z,
∴m+n∈M.故选 A.
答案:A
2.下列关于 0 与 说法不正确的是(
)
A.0
C.{0}=
B.0∈{0}
D.{0}
解析:因为 是不含任何元素的集合,故 A 正确,C 不正确;
对于选项 B,0∈{0},故 B 正确;对于选项 D,因为 是任何集合
的子集,所以{0} ,故 D 正确.故选 C.
答案:C
3.(2024 年四川期中考)已知集合 A={x|x2+ax+6<0},若1 A,
)
则 a 的取值范围为(
A.[-7,+∞)
C.(-∞,-7]
B.(-7,+∞)
D.(-∞,-7)
解析:由 1 A,可得12+a×1+6≥0,解得a≥-7,即a的
取值范围为[-7,+∞).故选 A.
答案:A
【题后反思】解决集合概念问题的关键有三点:一是确定构
成集合的元素;二是确定元素的限制条件;三是根据元素的特征
(满足的条件)构造关系式解决相应问题.
考点二 集合间的基本关系
则(
)
A.M N
B.N M
C.M=N
D.M∩N=
答案:B
(2)(2024 年广西北海期中考)已知集合 M 满足{-1,1} M
{-4,-1,1,2},则不同的 M 的个数为(
)
A.8
B.6
C.4
D.2
解析:由{-1,1} M {-4,-1,1,2}可知 M 可以是
{- 1,1},{-1,1,2},{-1,1,-4},{-1,1,2,-4},
故不同的 M 的个数为 4.
答案:C
(3)已知集合A={x|-3≤x≤4},B={x|2m-1≤x≤m+1},且
B A,则实数 m 的取值范围是________.
解析:∵B A,
①当 B= 时,2m-1>m+1,解得 m>2;
综上所述,实数 m 的取值范围是[-1,+∞).
答案:[-1,+∞)
【题后反思】判断集合间基本关系的方法
(1)列举法:用列举法表示集合,再从元素中寻求关系.
(2)化简集合法:用描述法表示的集合,若代表元素的表达式
比较复杂,往往需化简表达式,再寻求两个集合的关系.
特别提醒:在涉及集合关系时,必须优先考虑空集的情况,
否则会造成漏解.
【变式训练】
1.(2024 年天津期中考)若集合 A={2,3,4,5,6},则 A 的
真子集的个数为(
)
A.32
B.31
C.25
D.24
解析:集合 A={2,3,4,5,6}共有 5 个元素,所以集合 A
共有 25-1=31 个真子集.故选 B.
答案:B
2.(2023 年新课标Ⅱ卷)设集合 A={0,-a},B={1,a-2,
2a-2},若 A B,则 a=(
)
A.2
B.1
2
C.
3
D.-1
解析:依题意,a-2=0 或 2a-2=0,当 a-2=0 时,解得
a=2,此时 A={0,-2},B={1,0,2},不符合题意;当 2a-
2=0 时,解得 a=1,此时 A={0,-1},B={1,-1,0},符合
题意.故选 B.
答案:B
3.(2024 年陕西阶段练习)已知集合 A={1,2,3,4},B=
{x|-1≤x≤3},则 A∩B=(
A.{1,2}
C.{0,1,2}
)
B.{1,2,3}
D.{0,1,2,3}
解析:A={1,2,3,4},B={x|-1≤x≤3},则 A∩B={1,
2,3}.故选 B.
答案:B
考点三 集合的基本运算及运算性质
考向 1 集合的基本运算
通性通法:(1)一般来讲,集合中的元素若是离散的,可用
Venn图表示;数集中的元素若是连续的,则可用数轴表示,此时
要注意端点的情况.
(2)运算过程中要注意集合间的特殊关系的使用,灵活使用这
些关系,会使运算简化.
[例2](1)(2023 年湖北月考)已知全集 U=A∪B={x∈N|0<x+
1<6},A={1,2},若 A∩B= ,则 B=(
)
A.{0,3,4}
C.{-1,0}
B.{0,1}
D.{2,3,4}
解析:由题意,可得 U={x∈N|0<x+1<6}={0,1,2,3,
4},因为 U=A∪B,A∩B= ,A={1,2},所以 B={0,3,4}.
故选 A.
答案:A
(2)(2024 年山东阶段练习)设全集 U=R,A={x|-3≤x<4},
A.{x|x≤-2}
C.{x|x≥4}
B.{x|x>-2}
D.{x|x≤4}
又 A={x|-3≤x<4},所以 A∩B={x|-2≤x<4},所以图中阴
影部分表示的集合为 B(A∩B)={x|x≥4}.
答案:C
考向 2 利用集合的基本运算求参数
通性通法:利用集合的基本运算求参数的值或取值范围的
方法
(1)若集合中的元素能一一列举,则一般先用观察法得到不同
集合中元素之间的关系,再列方程(组)求解.
(2)与不等式有关的集合,一般利用数轴解决,要注意端点值
能否取到.
提醒:在求出参数后,注意结果的验证(满足互异性).
[例3](1)(2023 年河北衡水模拟) 已知集合 A ={x|y=ln (1-
x2)},B={x|x≤a},若( RA)∪B=R,则实数a的取值范围为( )
A.(1,+∞)
C.(-∞,1)
B.[1,+∞)
D.(-∞,1]
解析:由题可知A={x|y=ln (1-x2)}={x|-1
答案:B
(2)已知集合A={x|x2+x-6=0},B={x|mx+1=0},且A∩B
=B,则实数 m 的取值集合是________________.
解析:A={x|x2+x-6=0}={-3,2},
由 A∩B=B,知 B A.
当 B= 时,m=0,满足题意;
【考法全练】
1.(2024年四川期中考)已知集合A={x|-2≤x≤10},B= {x|1-m≤x≤1+m}.若B∩ RA= ,则实数m的取值范围为( )
A.0≤m≤3
B.0≤m≤9
C.m≥3或m≤9
D.3≤m≤9
答案:A
2.(多选题)已知全集U=Z,集合A={x|2x+1≥0,x∈Z},
B={-1,0,1,2},则( )
A.A∩B={0,1,2}
B.A∪B={x|x≥0}
C.( UA)∩B={-1}
D.A∩B的真子集个数是7
答案:ACD
3.(多选题)(2023 年湖南衡阳期末考)能正确表示图中阴影部分
的是(
)
A.B∩( UA) B.A∩( UB) C. (A∪B)A D. B(A∩B)
解析:因为阴影部分在 B 中不在 A 中,根据集合的运算分析
可知 ACD 正确.
答案:ACD
答案:AD
⊙集合的新定义问题的理解
“新定义”主要是指定义新概念、新公式、新定理、新法则、
新运算五种,然后根据此新定义去解决问题,有时还需要用类比
的方法去理解新定义.
答案:AC
【高分训练】
1.(2023 年云南保山模拟)定义集合运算:A+B={z|z=x+y,
x∈A,y∈B},设 A={1,2},B={1,2,3},则集合 A+B 的所
有元素之和为(
)
A.14
B.15
C.16
D.18
解析:由题设知 A+B={2,3,4,5},∴所有元素之和为 2
+3+4+5=14.故选 A.
答案:A
2.(2024 年天津阶段练习)设 M,P 是两个非空集合,规定 M-
)
P={x|x∈M 且 x P},根据这一规定,M-(M-P)等于(
A.M
B.P
C.M∪P
D.M∩P
解析:M-(M-P)={x|x∈M,且 x (M-P)},
用 venn 图表示集合 M,P 的关系如下图.
阴影部分为 M-P,所以 M-(M-P)=M∩P.故选 D.
答案:D
同课章节目录
