第八单元 数学广角——找次品 单元综合测试题 2024-2025学年下学期小学数学人教版五年级下册
文档属性
| 名称 | 第八单元 数学广角——找次品 单元综合测试题 2024-2025学年下学期小学数学人教版五年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 314.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 11:59:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第八单元 数学广角——找次品 单元综合测试题
2024-2025学年下学期小学数学人教版五年级下册
一、选择题
1.有9颗钢珠,其中8颗一样重,另有1颗比这8颗略轻,如果用一架天平最少称2次,就保证可以找到那颗较轻的钢珠,下列分组方法正确的是( )。
A.一定按(,,)分组
B.一定按(,,)分组
C.一定按(,,)分组
2.有26枚金币,其中一枚是假的(假金币轻一些)。要找出假金币,第一次用天平称,方法( )最好。
A.天平左右两边各放10枚,旁边放6枚
B.天平左右两边各放8枚,旁边放10枚
C.天平左右两边各放9枚,旁边放8枚
3.12个羽毛球特征相同,其中只有一个质量异常。现在要用一架没有砝码的天平去称,至少要称( )次才能找出那个质量异常的羽毛球。
A.4 B.3 C.2 D.1
4.有26盒饼干,其中的25盒质量相同,另有1盒少了几块。如果用天平称,至少称( )次就可以保证找出较轻的这盒饼干。
A.2 B.3 C.4 D.12
5.土笋冻是福建泉州的特色小吃,是一种由特有产品加工而成的冻品。李阿姨有28包土笋冻,其中27包质量相同,另有1包轻一些。如果用天平称,至少称( )次才能保证找出这包土笋冻。
A.1 B.2 C.3 D.4
6.8个球编号是1~8,其中6个球一样重,另外两个球都轻1克。为了找出这两个轻球,用天平称了3次,3次情况如图所示,两个轻球编号分别是( )。
A.③⑦ B.④⑦ C.③⑧ D.④⑧
二、填空题
7.有6个小球,其中一个是次品,要轻一些。仔细观察下图,( )号球是次品。
8.质检员李叔叔不小心把一包较轻的不合格饼干混入了26包合格产品中,假如用天平称,他至少要称( )次能保证找出这包不合格产品。
9.仓库里有10盒同一规格的零件,其中一盒用去了3个零件,但无法看出哪一盒是用过的,如果用一架没有砝码的天平称,最少需要称( )次能保证找出用过的那盒。
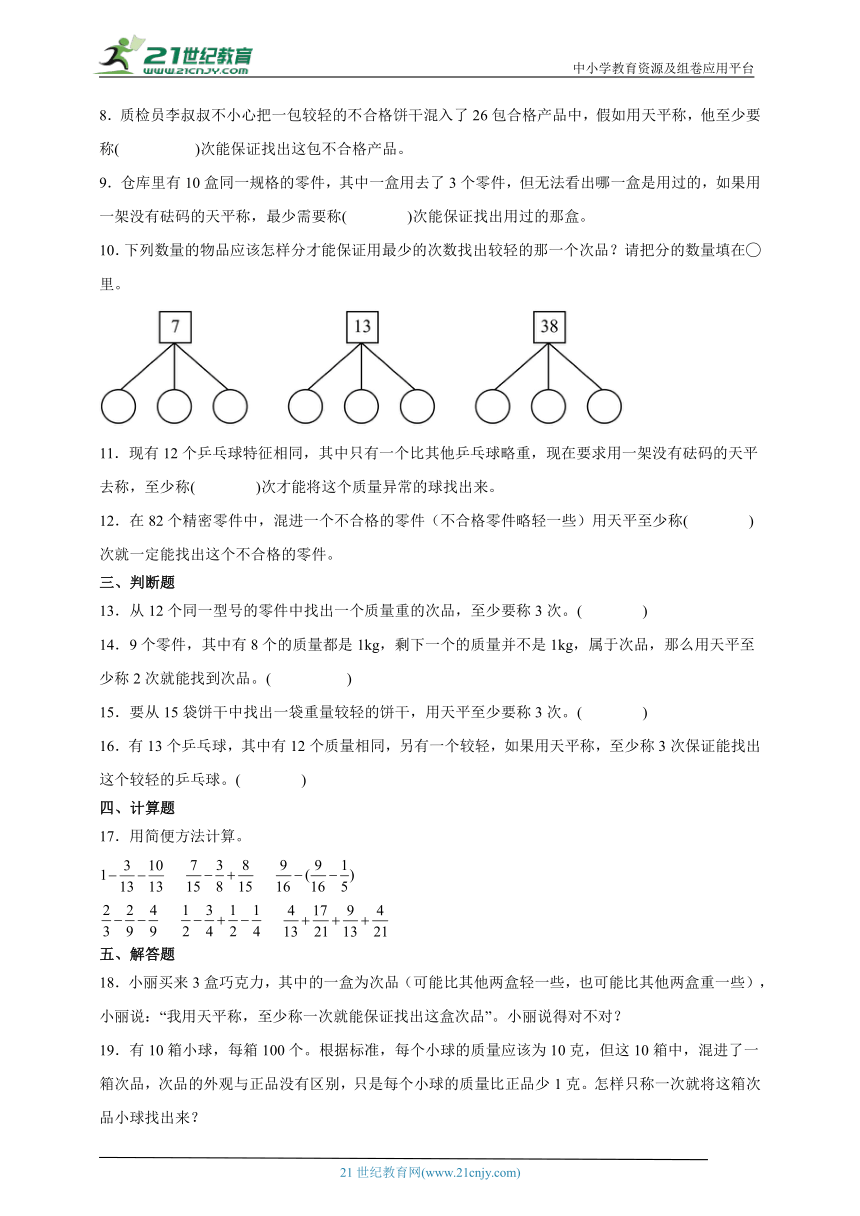
10.下列数量的物品应该怎样分才能保证用最少的次数找出较轻的那一个次品?请把分的数量填在 里。
11.现有12个乒乓球特征相同,其中只有一个比其他乒乓球略重,现在要求用一架没有砝码的天平去称,至少称( )次才能将这个质量异常的球找出来。
12.在82个精密零件中,混进一个不合格的零件(不合格零件略轻一些)用天平至少称( )次就一定能找出这个不合格的零件。
三、判断题
13.从12个同一型号的零件中找出一个质量重的次品,至少要称3次。( )
14.9个零件,其中有8个的质量都是1kg,剩下一个的质量并不是1kg,属于次品,那么用天平至少称2次就能找到次品。( )
15.要从15袋饼干中找出一袋重量较轻的饼干,用天平至少要称3次。( )
16.有13个乒乓球,其中有12个质量相同,另有一个较轻,如果用天平称,至少称3次保证能找出这个较轻的乒乓球。( )
四、计算题
17.用简便方法计算。
五、解答题
18.小丽买来3盒巧克力,其中的一盒为次品(可能比其他两盒轻一些,也可能比其他两盒重一些),小丽说:“我用天平称,至少称一次就能保证找出这盒次品”。小丽说得对不对?
19.有10箱小球,每箱100个。根据标准,每个小球的质量应该为10克,但这10箱中,混进了一箱次品,次品的外观与正品没有区别,只是每个小球的质量比正品少1克。怎样只称一次就将这箱次品小球找出来?
20.有3块月饼,其中2块各重40克,另外1块的质量不是40克,但不知道比40克轻还是重。你能利用天平把它找出来吗?说说你的想法。
21.有4枚外表完全相同的硬币,其中有3枚真币和1枚伪币,伪币与真币的重量不同,但是不知道伪币比真币轻还是重。现在只有一架没有砝码的天平。请问至少用天平称几次,就能保证弄清楚伪币究竟更轻还是重?
22.近年来我国新能源汽车制造业发展迅速,截止到2022年我国新能源汽车产销连续8年全球第一,这归功于新能源汽车制造企业的科技研发和精益求精。质检员王师傅发现19个零件中有一个不合格的零件,比其他零件轻一些,他用天平至少称几次能保证找到这个不合格的零件?
23.有个制造小球的工厂,生产了6箱小球,每个箱子里有100个小球。正品小球每个重10克,次品小球每个重11克。由于每个箱子里的小球由同一车间生产,如果一个箱子里有次品,则这个箱子里的球肯定都是次品。现在假设只有一个箱子里有次品,利用有砝码的天平,如何称一次把这个箱子找出来?
24.有61盒维生素C,其中1盒稍微轻一些,如果用天平称,至少称多少次就能保证找出这盒稍微轻一些的维生素C?(请用合适的方式简要表示出你的思考过程)
25.一个古玩商店经理不小心将一枚假铜币混入了10个真铜币中,这10枚真铜币外形、质量完全相同,假铜币外形与真铜币一样,只是质量不一样,但不知道比真铜币轻还是重。如果用天平称,至少称几次,就能保证帮助经理从11枚铜币中找出假铜币?你能用画图和文字写出你的称法吗?
参考答案
题号 1 2 3 4 5 6
答案 C C A B D B
1.C
【分析】找次品的最优策略:一是把待测物品分成3份;二是要尽量平均分,不能平均分的,应该使多的一份与少的一份只相差1,这样不但能保证找出次品,而且称的次数一定最少,据此解答。
【详解】有9颗钢珠,其中有一件是次品,比其它略轻。
第一次称重:先分成(3,3,3),天平两边各放3颗,①若天平平衡,则次品就在剩下的3颗中;②若天平不平衡,次品就在较轻的那3颗中;
第二次称重:把3颗分成(1,1,1),天平两边各放1颗,①若天平平衡,则次品就是剩下的1颗;②若天平不平衡,次品就是较轻的那1颗。
有9颗钢珠,其中8颗一样重,另有1颗比这8颗略轻,如果用一架天平最少称2次,就保证可以找到那颗较轻的钢珠,正确的分组方法是(,,)。
故答案为:C
2.C
【分析】根据找次品的方法,要尽量将物品平均分成3份来称,这样能较快找出次品。所以需要判断将26枚金币按各选项的分法,是否符合尽量平均分成3份的原则。
【详解】A.若天平左右两边各放10枚,旁边放6枚,此时分成的三份数量分别为10、10、6。10与6相差10-6=4,没有做到尽量平均分成3份。
B.若天平左右两边各放8枚,旁边放10枚分成的三份数量是8、8、10。10与8相差10-8=2,也没有做到尽量平均分成3份。
C.若天平左右两边各放9枚,旁边放8枚,分成的三份数量为9、9、8。9与8相差9-8=1,符合尽量平均分成3份,能使多的一份与少的一份相差1,这种分法最好。
所以第一次用天平称,天平左右两边各放9枚,旁边放8枚最好。
故答案为:C
3.A
【分析】根据题意,12个羽毛球特征相同,其中只有一个质量异常,但不知轻重,分组称重时,考虑天平平衡或不平衡时的各种情况,逐一讨论,得出至少称的次数。
【详解】第1次称量,将12个羽毛球平均分为三份①②③(每份4个),先把①和②放在天平的两边,如果天平平衡,则③里面有异常球;如果天平不平衡,则①和②中有异常羽毛球,③都是正常羽毛球;第2次称量,把①和②中的任意一份取下来,把③放上去,即可判断异常羽毛球在哪一份里,并且知道异常羽毛球的轻重;第3次称量,把有异常羽毛球的4个球平均分成两份(每份2个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球在哪一份里;第4次称量,再把有异常羽毛球的2个球分成两份(每份1个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球是哪一个。
所以至少要称4次才能找出那个质量异常的羽毛球。
故答案为:A
4.B
【分析】把26盒饼干分成3份,即(9,9,8);第一次称,天平两边各放9盒,如果天平不平衡,次品就在较轻的9盒中;如果天平平衡,次品在剩下的8盒中;考虑最不利原则,次品在数量多的里面,把有次品的9盒饼干平均分成3份,即(3,3,3),第二次称,天平两边各放3盒,如果天平不平衡,次品就在较轻的3盒中;如果天平平衡,次品在剩下的3盒中;把有次品的3盒饼干分成3份,即(1,1,1),第三次称,天平两边各放1盒,如果天平不平衡,次品就是较轻的那一盒;如果天平平衡,次品是剩下的那一盒。所以至少称3次保证找出较轻的这盒饼干。
【详解】
如果用天平称,至少称3次就可以保证找出较轻的这盒饼干。
故答案为:B
5.D
【分析】要达到次数最少,需要将要识别的物品的数目尽可能均匀的分成三份,然后每次称重时,需要将数目相等的两份放到天平两遍称重,不断识别,一直到找到次品为止。据此答题即可。
【详解】将28包分成3份:9,9,10;第一次称重,在天平两边各放9包,手里留10包;
(1)如果天平平衡,则次品在手里,将手里的10包分为3,3,4,在天平两边各放3包,手里留4包,
a.如果天平平衡,则次品在手里4包中,接下来,将手里的4包分为1,1,2,在天平两边各放1包,手里留2包,
①如果天平平衡,则次品在手里的2包,将这2包分别放在天平的两边就可以鉴别出次品;
②如果天平不平衡,则次品在升起的一边;
b.如果天平不平衡,则次品在升起的天平托盘的3包中,
接下来,将这3包分成三份:1,1,1。天平的两边分别放1包,手里留1包,称重第三次就可以鉴别出次品。
(2)如果天平不平衡,则次品在升起的天平托盘的9包中,将这9包分成三份:3,3,3,在天平两边各放3包,手里留3包,
a.如果天平不平衡,则找到次品在升起的天平托盘的3包中,
接下来,将这3包分成三份:1,1,1。天平的两边分别放1包,手里留1包,称重第三次就可以鉴别出次品。
b.如果天平平衡,则次品在手中的3包中。
接下来,将这3包分成三份:1,1,1。天平的两边分别放1包,手里留1包,称重第三次就可以鉴别出次品。
综上可得:至少称4次能就能保证可以找出这一包。
故答案为:D
【点睛】考查找次品的问题,分3份操作找到最优方法。
6.B
【分析】从第一次情况中可知,③和④里面有一个是轻的;如果③和④都是轻的,就不会出现第二种情况。
从第二次情况中可知,⑦和⑧里面有一个是轻的;
结合两种情况,①、②、⑤、⑥肯定是一样重的,①+③+⑦=②+④+⑥,假设④是标准的重量,则③是轻的,这个等式就不成立;假设③是标准的重量,则④是轻的,这个等式就不成立;为了保持等式成立,则⑦是轻的。
【详解】①+②比③+④重,说明③和④有一瓶矿泉水是次品(不能都是次品,因为若都是次品,那么不会出现:⑤+⑥比⑦+⑧重);
⑤+⑥比⑦+⑧重,说明:⑦和⑧有一瓶是次品(同理,不能都是次品);
根据:①+③+⑦与②+④+⑥一样重,
④和⑦是轻球。
故答案为:B
【点睛】推理就是由一个或几个已知的判断(前提),推导出一个未知的结论的思维过程。
解答简单推理题时,认真分析题目中的数量关系,寻找解题的突破口,然后再利用等量代换、消去等方法来进行解答。
7.⑤
【分析】用天平找次品,因为次品重量较轻,因此有次品的一端会上升,如果两端都没有次品,则天平会处于平衡状态,观察第一个天平,可知次品是④或⑤,再观察第二个天平,①④和②⑥平衡,说明这四个都不是次品,因此次品是⑤,据此分析。
【详解】根据分析,④⑤号轻一些,次品是④或⑤,又因为①、④、②、⑥都不是次品,因此⑤号球是次品。
8.3
【分析】要达到次数最少,需要将要识别的物品的数目尽可能均匀的分成三份,然后每次称重时,需要将数目相等的两份放到天平两边称重,不断识别,一直到找到次品为止。据此答题即可。
【详解】第一次:把27包饼干平均分成三份,每份9包,任取两份,分别放在天平秤两端,若天平秤平衡,则较轻的那包在未取的9包中,若天平秤不平衡,取较轻的一份继续称量;第二次:把含有较轻一包的9包饼干平均分成三份,每份3包,任取两份,分别放在天平秤两端,若天平秤平衡,则较轻的那包在未取的3包中,若天平秤不平衡,取较轻的一份继续称量;第三次:把含有较轻一包的3包饼干,任取2包,分别放在天平秤两端,若天平秤平衡,未取的那包即为较轻的,若天平秤不平衡,较高端的那包即为不合格的。则他至少要称3次能保证找出这包不合格产品。
9.3
【分析】第一次称:把10盒分成两组(5,5),天平两端各放一组,用过的那盒在轻的一边;
第二次称:把有用过的盒的那组5盒分成三组(2,2,1),天平两端各放2盒,平衡,用过的盒就是未称的一盒;不平衡,用过的盒在轻的一边;
第三次称:把有用过的一组2盒分成(1,1),天平两端各放1盒,用过的盒在轻的一边,因此,至少称3次可以保证找出用过的,据此解答。
【详解】根据分析可知,仓库里有10盒同一规格的零件,其中一盒用去了3个零件,但无法看出哪一盒是用过的,如果用一架没有砝码的天平称,最少需要称3次能保证找出用过的那盒。
10.见详解
【分析】要达到次数最少,需要将要识别的物品的数目尽可能均匀的分成三份,然后每次称重时,需要将数目相等的两份放到天平两边称重,不断识别,一直到找到次品为止。据此答题即可。
【详解】如图所示:
11.3
【分析】利用天平称重的方式,通过合理分组,逐步缩小范围,找出较重的那个乒乓球,关键在于每次分组后利用天平平衡与否确定次品所在组,从而确定最少的称重次数。
【详解】12分成(4,4,4),把任意两组的放在天平上称,可找出有次品的一组;再把有次品的一组4分成(2,2)放在天平上称,可找出有次品的一组;再把2分成(1,1),放在天平上称,可找出次品;共需3次。
所以至少称3次才能将这个质量异常的球找出来。
12.5
【分析】把82个分为27、27、28三组,第1次,各放27个,如果一样重,则在剩下的28里;把较轻的那组28个零件分为14、14两组,第2次在天平上两边各放14个,较轻的一组里有一个不合格的;第3次,把较轻的一组分为7、7两组,取出较轻的一组;第4次,较轻的那组7个零件分为3、3、1拿其中的3、3两组称;第5次,把较轻的那组3个零件分为1、1、1,3份,拿2份称,一样重就为剩下的那一个,不一样重,不足的就是我们要找的。
【详解】用天平至少称5次就一定能找出这个不合格的零件;
第一次:把82个零件分成(27、27、28)三组,如果两组27个零件一样重,则在剩下的28个里面;
第二次:28个分为(14、14)两组,找出较轻的那组;
第三次:14个分为(7、7)两组,找出较轻的那组;
第四次:7个分为(3、3、1)三组,拿出其中的3、3两组来称重;
第五次:3个分为(1、1、1)三份,拿2份称,一样重就为剩下的那一个;不一样重,不足的就是我们要找的。
【点睛】解答此题的关键是将零件进行合理的分组,逐次称量,进而找出次品;注意题目中说的是一定能找出这个不合格的零件。
13.√
【分析】把12个零件分成三份(4,4,4);
第一次:把其中两份分别放在天平两端,若天平平衡,则次品即在未取的4个零件中;若天平不平衡,次品在天平较低端的4个零件中;
第二次:含次品的4个零件,平均分成3份(1,1,2),把1个、1个分别放在天平两端,较低端的1个零件是次品;若平衡,则次品在另外2个零件中;
第三次:把含有次品的2个零件分别放在天平两端,较低端那个零件为次品,所以至少要称3次。据此解答。
【详解】根据分析可知,从12个同一型号的零件中找出一个质量重的次品,至少要称3次。
原题干说法正确。
故答案为:√
14.×
【分析】找次品的最优策略:一是把待测物品分成3份;二是要尽量平均分,不能平均分的,应该使多的一份与少的一份只相差1。这样不但能保证找出次品,而且称的次数一定最少。据此解答。
【详解】将9个零件平均分成3份,每份3个,任选其中的两份先称重,出现两种情况:
情况一:分成3组,每组3个,如果第一次测量的两组不平衡,说明次品在这其中,剩下一组是正品组的,那么进行第二次测量:①拿下轻的一组和正品组比,平衡的话,说明次品在重的那组,也说明了次品比正品重。②拿下轻的那组和正品比,不平衡的话,说明次品就在轻的这一组,也说明了次品比正品轻。找出次品所在的一组后,进行第三次测量,3个里面找出次品,只需要1次就够了。
情况二:第一次,如果天平平衡,说明不一样重的在剩下的3个零件里,把剩下的3个平均分成3份,每份1个,第二次称,任意选两份放在天平两边,又分两种情况:①天平平衡,说明剩下的1个是不一样的,共需称2次;②天平不平衡,还需要拿下一个再称一次,才能确定哪个质量不同,共需称3次。
综上,至少称3次能保证找出这个零件。
故答案为:×
【点睛】本题考查找次品问题,因为质量不同的零件不知道是轻还是重,需要多次称重才能确定次品在哪一份里,需分情况讨论。
15.√
【分析】把15袋饼干平均分成3份,每份5袋,即(5,5,5),第一次称,天平两边各放5袋,如果天平不平衡,次品就在较轻的5袋中;如果天平平衡,次品在剩下的5袋中;再把有次品的5袋饼干分成(2,2,1),第二次称,天平两边各放2袋,如果天平不平衡,次品在较轻的2袋中;如果天平平衡,次品就是剩下的那一袋;考虑最不利原则,次品在数量多的里面,最后把有次品的2袋饼干分成(1,1),第三次称,天平两边各放1袋,次品就是较轻的那一袋。至少称3次能保证找出这袋较轻的饼干。
【详解】
故答案为:√
【点睛】找次品的最优策略:一是把待测物品分成3份;二是要尽量平均分,不能平均分的,应该使多的一份与少的一份只相差1。这样不但能保证找出次品,而且称的次数一定最少。
16.√
【分析】找次品的方法:一般是把待测物品分成3份,能平均分的就平均分,不能平均分的,使其中的2份相同,第3份尽量与这两份相同,再称其中的2份,根据天平平衡、不平衡进行判断,如果不能找出次品,继续把含有次品的份数再分成3份,方法同上,直到找出次品。
找次品的公式计算规律:
2~3个物品称1次;
4~9个物品称2次;
10~27个物品称3次;
28~81个物品称4次(以上是知道次品轻重的,不知道次品轻重要称多一次)。
……
【详解】13在10~27个之间,由分析可知,10~27个物品至少称3次。
所以原题说法正确。
故答案为:√
17.0;;
0;0;2
【分析】根据减法的性质,减去两个数相当于减去这两个数的和;
分数的简便计算,先将同分母分数相加减,即可以利用交换律,将换到前面,注意再在交换位置时,要将数字前面的运算符号一起换位置;
先将括号去掉,由于括号前面是减号,去掉括号时,要将括号里面的减号变成加号;
根据减法的性质,减去两个数相当于减去这两个数的和;
将利用交换律和结合律将同分母分数先相加,即可简便计算;
连加时,利用加法的交换律和结合律将同分母分数先相加即可简便计算。
【详解】
18.不对
【分析】如图示,第一种情况,看图1,天平称红色和绿色的巧克力,天平是平衡的,可以确定没有次品。第二种情况,看图2,红色和绿色一起称,天平向红色这边倾斜,仍然不知道哪个才是次品,第三种情况,看图3,蓝色和绿色一起称,天平向蓝色这边倾斜,结合前面2种情况,绿色比红色和蓝色都要轻,据此判断,绿色巧克力是次品。
图1 图2 图3
【详解】根据题意,小丽说的至少称一次就能保证找出这盒次品,因为不确定哪个是次品至少要称2次,才能找到次品,所以小丽说的不对。
答:小丽说的不对。
19.见详解
【分析】把箱子按1~10的顺序编上号码,1号箱取1个小球,2号箱取2个小球,3号箱取3个小球, ,10号箱取10个小球。1+2+3+ +10=55个,55×10=550(克),称出的质量比550克少几克,次品就是几号箱,据此解答。
【详解】1+2+3+4+5+6+7+8+9+10
=(1+10)+(2+9)+(3+8)+(4+7)+(5+6)
=11+11+11+11+11
=11×5
=55(个)
55×10=550(克)
答:称出的质量比550克少几克,次品就是几号箱,这样只称一次就可以将这箱次品小球找出来。
【点睛】本题考查找次品问题,明确每个小球的质量比正品少1克是解题的关键。
20.见详解
【分析】天平是用来称量物体质量的工具,此题并不是称量物体的质量,而是使用天平来比较物体质量的大小,所以,在调好的天平两盘中分别放上物体,当哪边的托盘上升,则说明这边托盘中的物体质量偏小。
【详解】把其中两块放在天平上。如果天平两边平衡说明这就是两块40克的月饼。
再把40克的一块月饼放在天平一端,把另一块不知多重的放在另一端,如果另一端下降,说明另一块比40克重,如果端上升,说明另一块比40克轻。
而把其中两块放在天平上。如果天平两边不平衡,说明这就是两块有一块是40克的月饼,另一块不是40克。
再把在天平上升一端的一块月饼放在天平一端,把第三块月饼放在另一端,如果天平平衡,说明这两块都是40克重,刚才在天平下降那端的那一块比40克重。
如果把第三块月饼放在另一端,天平不平衡,则第三块月饼这端必定下降,则第三块月饼和第一次在天平下降端的都是40克的月饼,而另一块比40克轻。
这样,至少两次就一定可以找出来,并且知道它比40克重还是轻。
【点睛】该题考查了利用天平判断物体质量的技能,需要学生开动脑筋,借助一定的数学思维方式进行解答。
21.2次
【分析】本题的目的是弄清楚伪币比真币轻还是重,但在称时我们还是可以使用三分法来分物品,把4枚硬币分为(1,1,2)先称数量相同的两份,再根据情况称剩下的一份(方法不唯一)。
【详解】 把4枚硬币分为(1,1,2),第一次称前两份:若天平平衡,说明这两枚都是真币,把这两枚放在天平一端,剩下一份(有伪币)放在另一端称第二次:若伪币这端更轻说明伪币比真币轻,反之则更重。 若天平不平衡,说明这两枚中有一枚是假币,剩下的一份为真币,分别放在天平两端称第二次:若伪币这端更轻说明伪币比真币轻,反之则更重。(方法不唯一)
答:至少用天平称2次,就能保证弄清楚伪币究竟更轻还是重。
22.3次
【分析】找次品的最优策略:(1)把待分物品分成3份;(2)每份数量尽量平均,如果不能平均分的,也应该使多的一份与少的一份只相差1。
【详解】将19个零件分成(6、6、7),先称(6、6),只考虑最不利的情况,即次品在多的里面,即次品在7个中;将7个分成(2、2、3),先称(2、2),考虑最不利的情况,即次品在3个中;将3个分成(1、1、1),称(1、1),无论平衡不平衡都可确定次品,共3次。
答:他用天平至少称3次能保证找到这个不合格的零件。
23.见详解
【分析】本题的解题关键在于给每个箱子设置不同点,通过不同点来确定箱子,如(方法不唯一):给六个箱子分别编号1、2、3、4、5、6号,从每个箱子里取出对应编号数量的小球,共取21个,给这21个小球称重,实际重量必然大于210克,根据多出的重量即可确定次品箱。
【详解】给六个箱子分别编号1、2、3、4、5、6号,从每个箱子里取出对应编号数量的小球,共取出:1+2+3+4+5+6=21(个)
应重:21×10=210(克)
实际重量必定多于210克,多了几克,几号箱中就是次品(如:若5号箱重为次品,那就会多5克,实际重量为215克。)
24.4次
【分析】将61盒分成20盒、20盒、21盒,称量同是20盒的两份,找出轻的一盒在哪份里面。若轻的一盒在20盒这份,将20盒分成7盒、7盒、6盒,称量同是7盒的两份,找出轻的一盒在哪份里面;同理若轻的一盒在21盒这份,将21盒分成7盒、7盒、7盒,任意称量同是7盒的两份,找出轻的一盒在哪份里面。以此类推直到找出次品为止,就能知道至少称量几次能找出轻的一盒。
【详解】第一次称量:将61盒分成20盒、20盒、21盒,找到轻的一盒在哪份里面;
第二次称量:将20盒分成7盒、7盒、6盒,找到轻的一盒在哪份里面;或者将21盒分成7盒、7盒、7盒,任意称量同是7盒的两份,找出轻的一盒在哪份里面;
第三次称量:找到6盒或者7盒里轻的一盒;
第四次称量:找到2盒或者3盒里轻的一盒。
答:至少称量4次能找出轻的一盒。
【点睛】本题考查运用优化策略找次品问题,找次品时,把物体分成3份,每份数量尽量平均时,可以保证所称量的次数最少。
25.至少称4次;
将11枚硬币分成(4、4、3),先称两个4枚,①平衡,次品在3个中,将3个分成(1、1、1),称两个,平衡剩下一个是次品,不平衡,随便拿下一个与剩下的称,即可找出次品;②不平衡,次品在4个中,随便拿出一个放到3个里,确定在哪4个,再称两次确定次品是轻还是重,再称一次即可。
【分析】找次品的最优策略:
(1)把待分物品分成3份;
(2)每份数量尽量平均,如果不能平均分的,也应该使多的一份与少的一份只相差1。
【详解】将11枚硬币分成(4、4、3),先称两个4枚,①平衡,次品在3个中,将3个分成(1、1、1),称两个,平衡剩下一个是次品,不平衡,随便拿下一个与剩下的称,即可找出次品;②不平衡,次品在4个中,随便拿出一个放到3个里,确定在哪4个,再称两次确定次品是轻还是重,再称一次即可。
答:至少称4次。
【点睛】本题考查了找次品,不知道轻重,要确定次品是轻还是重。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八单元 数学广角——找次品 单元综合测试题
2024-2025学年下学期小学数学人教版五年级下册
一、选择题
1.有9颗钢珠,其中8颗一样重,另有1颗比这8颗略轻,如果用一架天平最少称2次,就保证可以找到那颗较轻的钢珠,下列分组方法正确的是( )。
A.一定按(,,)分组
B.一定按(,,)分组
C.一定按(,,)分组
2.有26枚金币,其中一枚是假的(假金币轻一些)。要找出假金币,第一次用天平称,方法( )最好。
A.天平左右两边各放10枚,旁边放6枚
B.天平左右两边各放8枚,旁边放10枚
C.天平左右两边各放9枚,旁边放8枚
3.12个羽毛球特征相同,其中只有一个质量异常。现在要用一架没有砝码的天平去称,至少要称( )次才能找出那个质量异常的羽毛球。
A.4 B.3 C.2 D.1
4.有26盒饼干,其中的25盒质量相同,另有1盒少了几块。如果用天平称,至少称( )次就可以保证找出较轻的这盒饼干。
A.2 B.3 C.4 D.12
5.土笋冻是福建泉州的特色小吃,是一种由特有产品加工而成的冻品。李阿姨有28包土笋冻,其中27包质量相同,另有1包轻一些。如果用天平称,至少称( )次才能保证找出这包土笋冻。
A.1 B.2 C.3 D.4
6.8个球编号是1~8,其中6个球一样重,另外两个球都轻1克。为了找出这两个轻球,用天平称了3次,3次情况如图所示,两个轻球编号分别是( )。
A.③⑦ B.④⑦ C.③⑧ D.④⑧
二、填空题
7.有6个小球,其中一个是次品,要轻一些。仔细观察下图,( )号球是次品。
8.质检员李叔叔不小心把一包较轻的不合格饼干混入了26包合格产品中,假如用天平称,他至少要称( )次能保证找出这包不合格产品。
9.仓库里有10盒同一规格的零件,其中一盒用去了3个零件,但无法看出哪一盒是用过的,如果用一架没有砝码的天平称,最少需要称( )次能保证找出用过的那盒。
10.下列数量的物品应该怎样分才能保证用最少的次数找出较轻的那一个次品?请把分的数量填在 里。
11.现有12个乒乓球特征相同,其中只有一个比其他乒乓球略重,现在要求用一架没有砝码的天平去称,至少称( )次才能将这个质量异常的球找出来。
12.在82个精密零件中,混进一个不合格的零件(不合格零件略轻一些)用天平至少称( )次就一定能找出这个不合格的零件。
三、判断题
13.从12个同一型号的零件中找出一个质量重的次品,至少要称3次。( )
14.9个零件,其中有8个的质量都是1kg,剩下一个的质量并不是1kg,属于次品,那么用天平至少称2次就能找到次品。( )
15.要从15袋饼干中找出一袋重量较轻的饼干,用天平至少要称3次。( )
16.有13个乒乓球,其中有12个质量相同,另有一个较轻,如果用天平称,至少称3次保证能找出这个较轻的乒乓球。( )
四、计算题
17.用简便方法计算。
五、解答题
18.小丽买来3盒巧克力,其中的一盒为次品(可能比其他两盒轻一些,也可能比其他两盒重一些),小丽说:“我用天平称,至少称一次就能保证找出这盒次品”。小丽说得对不对?
19.有10箱小球,每箱100个。根据标准,每个小球的质量应该为10克,但这10箱中,混进了一箱次品,次品的外观与正品没有区别,只是每个小球的质量比正品少1克。怎样只称一次就将这箱次品小球找出来?
20.有3块月饼,其中2块各重40克,另外1块的质量不是40克,但不知道比40克轻还是重。你能利用天平把它找出来吗?说说你的想法。
21.有4枚外表完全相同的硬币,其中有3枚真币和1枚伪币,伪币与真币的重量不同,但是不知道伪币比真币轻还是重。现在只有一架没有砝码的天平。请问至少用天平称几次,就能保证弄清楚伪币究竟更轻还是重?
22.近年来我国新能源汽车制造业发展迅速,截止到2022年我国新能源汽车产销连续8年全球第一,这归功于新能源汽车制造企业的科技研发和精益求精。质检员王师傅发现19个零件中有一个不合格的零件,比其他零件轻一些,他用天平至少称几次能保证找到这个不合格的零件?
23.有个制造小球的工厂,生产了6箱小球,每个箱子里有100个小球。正品小球每个重10克,次品小球每个重11克。由于每个箱子里的小球由同一车间生产,如果一个箱子里有次品,则这个箱子里的球肯定都是次品。现在假设只有一个箱子里有次品,利用有砝码的天平,如何称一次把这个箱子找出来?
24.有61盒维生素C,其中1盒稍微轻一些,如果用天平称,至少称多少次就能保证找出这盒稍微轻一些的维生素C?(请用合适的方式简要表示出你的思考过程)
25.一个古玩商店经理不小心将一枚假铜币混入了10个真铜币中,这10枚真铜币外形、质量完全相同,假铜币外形与真铜币一样,只是质量不一样,但不知道比真铜币轻还是重。如果用天平称,至少称几次,就能保证帮助经理从11枚铜币中找出假铜币?你能用画图和文字写出你的称法吗?
参考答案
题号 1 2 3 4 5 6
答案 C C A B D B
1.C
【分析】找次品的最优策略:一是把待测物品分成3份;二是要尽量平均分,不能平均分的,应该使多的一份与少的一份只相差1,这样不但能保证找出次品,而且称的次数一定最少,据此解答。
【详解】有9颗钢珠,其中有一件是次品,比其它略轻。
第一次称重:先分成(3,3,3),天平两边各放3颗,①若天平平衡,则次品就在剩下的3颗中;②若天平不平衡,次品就在较轻的那3颗中;
第二次称重:把3颗分成(1,1,1),天平两边各放1颗,①若天平平衡,则次品就是剩下的1颗;②若天平不平衡,次品就是较轻的那1颗。
有9颗钢珠,其中8颗一样重,另有1颗比这8颗略轻,如果用一架天平最少称2次,就保证可以找到那颗较轻的钢珠,正确的分组方法是(,,)。
故答案为:C
2.C
【分析】根据找次品的方法,要尽量将物品平均分成3份来称,这样能较快找出次品。所以需要判断将26枚金币按各选项的分法,是否符合尽量平均分成3份的原则。
【详解】A.若天平左右两边各放10枚,旁边放6枚,此时分成的三份数量分别为10、10、6。10与6相差10-6=4,没有做到尽量平均分成3份。
B.若天平左右两边各放8枚,旁边放10枚分成的三份数量是8、8、10。10与8相差10-8=2,也没有做到尽量平均分成3份。
C.若天平左右两边各放9枚,旁边放8枚,分成的三份数量为9、9、8。9与8相差9-8=1,符合尽量平均分成3份,能使多的一份与少的一份相差1,这种分法最好。
所以第一次用天平称,天平左右两边各放9枚,旁边放8枚最好。
故答案为:C
3.A
【分析】根据题意,12个羽毛球特征相同,其中只有一个质量异常,但不知轻重,分组称重时,考虑天平平衡或不平衡时的各种情况,逐一讨论,得出至少称的次数。
【详解】第1次称量,将12个羽毛球平均分为三份①②③(每份4个),先把①和②放在天平的两边,如果天平平衡,则③里面有异常球;如果天平不平衡,则①和②中有异常羽毛球,③都是正常羽毛球;第2次称量,把①和②中的任意一份取下来,把③放上去,即可判断异常羽毛球在哪一份里,并且知道异常羽毛球的轻重;第3次称量,把有异常羽毛球的4个球平均分成两份(每份2个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球在哪一份里;第4次称量,再把有异常羽毛球的2个球分成两份(每份1个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球是哪一个。
所以至少要称4次才能找出那个质量异常的羽毛球。
故答案为:A
4.B
【分析】把26盒饼干分成3份,即(9,9,8);第一次称,天平两边各放9盒,如果天平不平衡,次品就在较轻的9盒中;如果天平平衡,次品在剩下的8盒中;考虑最不利原则,次品在数量多的里面,把有次品的9盒饼干平均分成3份,即(3,3,3),第二次称,天平两边各放3盒,如果天平不平衡,次品就在较轻的3盒中;如果天平平衡,次品在剩下的3盒中;把有次品的3盒饼干分成3份,即(1,1,1),第三次称,天平两边各放1盒,如果天平不平衡,次品就是较轻的那一盒;如果天平平衡,次品是剩下的那一盒。所以至少称3次保证找出较轻的这盒饼干。
【详解】
如果用天平称,至少称3次就可以保证找出较轻的这盒饼干。
故答案为:B
5.D
【分析】要达到次数最少,需要将要识别的物品的数目尽可能均匀的分成三份,然后每次称重时,需要将数目相等的两份放到天平两遍称重,不断识别,一直到找到次品为止。据此答题即可。
【详解】将28包分成3份:9,9,10;第一次称重,在天平两边各放9包,手里留10包;
(1)如果天平平衡,则次品在手里,将手里的10包分为3,3,4,在天平两边各放3包,手里留4包,
a.如果天平平衡,则次品在手里4包中,接下来,将手里的4包分为1,1,2,在天平两边各放1包,手里留2包,
①如果天平平衡,则次品在手里的2包,将这2包分别放在天平的两边就可以鉴别出次品;
②如果天平不平衡,则次品在升起的一边;
b.如果天平不平衡,则次品在升起的天平托盘的3包中,
接下来,将这3包分成三份:1,1,1。天平的两边分别放1包,手里留1包,称重第三次就可以鉴别出次品。
(2)如果天平不平衡,则次品在升起的天平托盘的9包中,将这9包分成三份:3,3,3,在天平两边各放3包,手里留3包,
a.如果天平不平衡,则找到次品在升起的天平托盘的3包中,
接下来,将这3包分成三份:1,1,1。天平的两边分别放1包,手里留1包,称重第三次就可以鉴别出次品。
b.如果天平平衡,则次品在手中的3包中。
接下来,将这3包分成三份:1,1,1。天平的两边分别放1包,手里留1包,称重第三次就可以鉴别出次品。
综上可得:至少称4次能就能保证可以找出这一包。
故答案为:D
【点睛】考查找次品的问题,分3份操作找到最优方法。
6.B
【分析】从第一次情况中可知,③和④里面有一个是轻的;如果③和④都是轻的,就不会出现第二种情况。
从第二次情况中可知,⑦和⑧里面有一个是轻的;
结合两种情况,①、②、⑤、⑥肯定是一样重的,①+③+⑦=②+④+⑥,假设④是标准的重量,则③是轻的,这个等式就不成立;假设③是标准的重量,则④是轻的,这个等式就不成立;为了保持等式成立,则⑦是轻的。
【详解】①+②比③+④重,说明③和④有一瓶矿泉水是次品(不能都是次品,因为若都是次品,那么不会出现:⑤+⑥比⑦+⑧重);
⑤+⑥比⑦+⑧重,说明:⑦和⑧有一瓶是次品(同理,不能都是次品);
根据:①+③+⑦与②+④+⑥一样重,
④和⑦是轻球。
故答案为:B
【点睛】推理就是由一个或几个已知的判断(前提),推导出一个未知的结论的思维过程。
解答简单推理题时,认真分析题目中的数量关系,寻找解题的突破口,然后再利用等量代换、消去等方法来进行解答。
7.⑤
【分析】用天平找次品,因为次品重量较轻,因此有次品的一端会上升,如果两端都没有次品,则天平会处于平衡状态,观察第一个天平,可知次品是④或⑤,再观察第二个天平,①④和②⑥平衡,说明这四个都不是次品,因此次品是⑤,据此分析。
【详解】根据分析,④⑤号轻一些,次品是④或⑤,又因为①、④、②、⑥都不是次品,因此⑤号球是次品。
8.3
【分析】要达到次数最少,需要将要识别的物品的数目尽可能均匀的分成三份,然后每次称重时,需要将数目相等的两份放到天平两边称重,不断识别,一直到找到次品为止。据此答题即可。
【详解】第一次:把27包饼干平均分成三份,每份9包,任取两份,分别放在天平秤两端,若天平秤平衡,则较轻的那包在未取的9包中,若天平秤不平衡,取较轻的一份继续称量;第二次:把含有较轻一包的9包饼干平均分成三份,每份3包,任取两份,分别放在天平秤两端,若天平秤平衡,则较轻的那包在未取的3包中,若天平秤不平衡,取较轻的一份继续称量;第三次:把含有较轻一包的3包饼干,任取2包,分别放在天平秤两端,若天平秤平衡,未取的那包即为较轻的,若天平秤不平衡,较高端的那包即为不合格的。则他至少要称3次能保证找出这包不合格产品。
9.3
【分析】第一次称:把10盒分成两组(5,5),天平两端各放一组,用过的那盒在轻的一边;
第二次称:把有用过的盒的那组5盒分成三组(2,2,1),天平两端各放2盒,平衡,用过的盒就是未称的一盒;不平衡,用过的盒在轻的一边;
第三次称:把有用过的一组2盒分成(1,1),天平两端各放1盒,用过的盒在轻的一边,因此,至少称3次可以保证找出用过的,据此解答。
【详解】根据分析可知,仓库里有10盒同一规格的零件,其中一盒用去了3个零件,但无法看出哪一盒是用过的,如果用一架没有砝码的天平称,最少需要称3次能保证找出用过的那盒。
10.见详解
【分析】要达到次数最少,需要将要识别的物品的数目尽可能均匀的分成三份,然后每次称重时,需要将数目相等的两份放到天平两边称重,不断识别,一直到找到次品为止。据此答题即可。
【详解】如图所示:
11.3
【分析】利用天平称重的方式,通过合理分组,逐步缩小范围,找出较重的那个乒乓球,关键在于每次分组后利用天平平衡与否确定次品所在组,从而确定最少的称重次数。
【详解】12分成(4,4,4),把任意两组的放在天平上称,可找出有次品的一组;再把有次品的一组4分成(2,2)放在天平上称,可找出有次品的一组;再把2分成(1,1),放在天平上称,可找出次品;共需3次。
所以至少称3次才能将这个质量异常的球找出来。
12.5
【分析】把82个分为27、27、28三组,第1次,各放27个,如果一样重,则在剩下的28里;把较轻的那组28个零件分为14、14两组,第2次在天平上两边各放14个,较轻的一组里有一个不合格的;第3次,把较轻的一组分为7、7两组,取出较轻的一组;第4次,较轻的那组7个零件分为3、3、1拿其中的3、3两组称;第5次,把较轻的那组3个零件分为1、1、1,3份,拿2份称,一样重就为剩下的那一个,不一样重,不足的就是我们要找的。
【详解】用天平至少称5次就一定能找出这个不合格的零件;
第一次:把82个零件分成(27、27、28)三组,如果两组27个零件一样重,则在剩下的28个里面;
第二次:28个分为(14、14)两组,找出较轻的那组;
第三次:14个分为(7、7)两组,找出较轻的那组;
第四次:7个分为(3、3、1)三组,拿出其中的3、3两组来称重;
第五次:3个分为(1、1、1)三份,拿2份称,一样重就为剩下的那一个;不一样重,不足的就是我们要找的。
【点睛】解答此题的关键是将零件进行合理的分组,逐次称量,进而找出次品;注意题目中说的是一定能找出这个不合格的零件。
13.√
【分析】把12个零件分成三份(4,4,4);
第一次:把其中两份分别放在天平两端,若天平平衡,则次品即在未取的4个零件中;若天平不平衡,次品在天平较低端的4个零件中;
第二次:含次品的4个零件,平均分成3份(1,1,2),把1个、1个分别放在天平两端,较低端的1个零件是次品;若平衡,则次品在另外2个零件中;
第三次:把含有次品的2个零件分别放在天平两端,较低端那个零件为次品,所以至少要称3次。据此解答。
【详解】根据分析可知,从12个同一型号的零件中找出一个质量重的次品,至少要称3次。
原题干说法正确。
故答案为:√
14.×
【分析】找次品的最优策略:一是把待测物品分成3份;二是要尽量平均分,不能平均分的,应该使多的一份与少的一份只相差1。这样不但能保证找出次品,而且称的次数一定最少。据此解答。
【详解】将9个零件平均分成3份,每份3个,任选其中的两份先称重,出现两种情况:
情况一:分成3组,每组3个,如果第一次测量的两组不平衡,说明次品在这其中,剩下一组是正品组的,那么进行第二次测量:①拿下轻的一组和正品组比,平衡的话,说明次品在重的那组,也说明了次品比正品重。②拿下轻的那组和正品比,不平衡的话,说明次品就在轻的这一组,也说明了次品比正品轻。找出次品所在的一组后,进行第三次测量,3个里面找出次品,只需要1次就够了。
情况二:第一次,如果天平平衡,说明不一样重的在剩下的3个零件里,把剩下的3个平均分成3份,每份1个,第二次称,任意选两份放在天平两边,又分两种情况:①天平平衡,说明剩下的1个是不一样的,共需称2次;②天平不平衡,还需要拿下一个再称一次,才能确定哪个质量不同,共需称3次。
综上,至少称3次能保证找出这个零件。
故答案为:×
【点睛】本题考查找次品问题,因为质量不同的零件不知道是轻还是重,需要多次称重才能确定次品在哪一份里,需分情况讨论。
15.√
【分析】把15袋饼干平均分成3份,每份5袋,即(5,5,5),第一次称,天平两边各放5袋,如果天平不平衡,次品就在较轻的5袋中;如果天平平衡,次品在剩下的5袋中;再把有次品的5袋饼干分成(2,2,1),第二次称,天平两边各放2袋,如果天平不平衡,次品在较轻的2袋中;如果天平平衡,次品就是剩下的那一袋;考虑最不利原则,次品在数量多的里面,最后把有次品的2袋饼干分成(1,1),第三次称,天平两边各放1袋,次品就是较轻的那一袋。至少称3次能保证找出这袋较轻的饼干。
【详解】
故答案为:√
【点睛】找次品的最优策略:一是把待测物品分成3份;二是要尽量平均分,不能平均分的,应该使多的一份与少的一份只相差1。这样不但能保证找出次品,而且称的次数一定最少。
16.√
【分析】找次品的方法:一般是把待测物品分成3份,能平均分的就平均分,不能平均分的,使其中的2份相同,第3份尽量与这两份相同,再称其中的2份,根据天平平衡、不平衡进行判断,如果不能找出次品,继续把含有次品的份数再分成3份,方法同上,直到找出次品。
找次品的公式计算规律:
2~3个物品称1次;
4~9个物品称2次;
10~27个物品称3次;
28~81个物品称4次(以上是知道次品轻重的,不知道次品轻重要称多一次)。
……
【详解】13在10~27个之间,由分析可知,10~27个物品至少称3次。
所以原题说法正确。
故答案为:√
17.0;;
0;0;2
【分析】根据减法的性质,减去两个数相当于减去这两个数的和;
分数的简便计算,先将同分母分数相加减,即可以利用交换律,将换到前面,注意再在交换位置时,要将数字前面的运算符号一起换位置;
先将括号去掉,由于括号前面是减号,去掉括号时,要将括号里面的减号变成加号;
根据减法的性质,减去两个数相当于减去这两个数的和;
将利用交换律和结合律将同分母分数先相加,即可简便计算;
连加时,利用加法的交换律和结合律将同分母分数先相加即可简便计算。
【详解】
18.不对
【分析】如图示,第一种情况,看图1,天平称红色和绿色的巧克力,天平是平衡的,可以确定没有次品。第二种情况,看图2,红色和绿色一起称,天平向红色这边倾斜,仍然不知道哪个才是次品,第三种情况,看图3,蓝色和绿色一起称,天平向蓝色这边倾斜,结合前面2种情况,绿色比红色和蓝色都要轻,据此判断,绿色巧克力是次品。
图1 图2 图3
【详解】根据题意,小丽说的至少称一次就能保证找出这盒次品,因为不确定哪个是次品至少要称2次,才能找到次品,所以小丽说的不对。
答:小丽说的不对。
19.见详解
【分析】把箱子按1~10的顺序编上号码,1号箱取1个小球,2号箱取2个小球,3号箱取3个小球, ,10号箱取10个小球。1+2+3+ +10=55个,55×10=550(克),称出的质量比550克少几克,次品就是几号箱,据此解答。
【详解】1+2+3+4+5+6+7+8+9+10
=(1+10)+(2+9)+(3+8)+(4+7)+(5+6)
=11+11+11+11+11
=11×5
=55(个)
55×10=550(克)
答:称出的质量比550克少几克,次品就是几号箱,这样只称一次就可以将这箱次品小球找出来。
【点睛】本题考查找次品问题,明确每个小球的质量比正品少1克是解题的关键。
20.见详解
【分析】天平是用来称量物体质量的工具,此题并不是称量物体的质量,而是使用天平来比较物体质量的大小,所以,在调好的天平两盘中分别放上物体,当哪边的托盘上升,则说明这边托盘中的物体质量偏小。
【详解】把其中两块放在天平上。如果天平两边平衡说明这就是两块40克的月饼。
再把40克的一块月饼放在天平一端,把另一块不知多重的放在另一端,如果另一端下降,说明另一块比40克重,如果端上升,说明另一块比40克轻。
而把其中两块放在天平上。如果天平两边不平衡,说明这就是两块有一块是40克的月饼,另一块不是40克。
再把在天平上升一端的一块月饼放在天平一端,把第三块月饼放在另一端,如果天平平衡,说明这两块都是40克重,刚才在天平下降那端的那一块比40克重。
如果把第三块月饼放在另一端,天平不平衡,则第三块月饼这端必定下降,则第三块月饼和第一次在天平下降端的都是40克的月饼,而另一块比40克轻。
这样,至少两次就一定可以找出来,并且知道它比40克重还是轻。
【点睛】该题考查了利用天平判断物体质量的技能,需要学生开动脑筋,借助一定的数学思维方式进行解答。
21.2次
【分析】本题的目的是弄清楚伪币比真币轻还是重,但在称时我们还是可以使用三分法来分物品,把4枚硬币分为(1,1,2)先称数量相同的两份,再根据情况称剩下的一份(方法不唯一)。
【详解】 把4枚硬币分为(1,1,2),第一次称前两份:若天平平衡,说明这两枚都是真币,把这两枚放在天平一端,剩下一份(有伪币)放在另一端称第二次:若伪币这端更轻说明伪币比真币轻,反之则更重。 若天平不平衡,说明这两枚中有一枚是假币,剩下的一份为真币,分别放在天平两端称第二次:若伪币这端更轻说明伪币比真币轻,反之则更重。(方法不唯一)
答:至少用天平称2次,就能保证弄清楚伪币究竟更轻还是重。
22.3次
【分析】找次品的最优策略:(1)把待分物品分成3份;(2)每份数量尽量平均,如果不能平均分的,也应该使多的一份与少的一份只相差1。
【详解】将19个零件分成(6、6、7),先称(6、6),只考虑最不利的情况,即次品在多的里面,即次品在7个中;将7个分成(2、2、3),先称(2、2),考虑最不利的情况,即次品在3个中;将3个分成(1、1、1),称(1、1),无论平衡不平衡都可确定次品,共3次。
答:他用天平至少称3次能保证找到这个不合格的零件。
23.见详解
【分析】本题的解题关键在于给每个箱子设置不同点,通过不同点来确定箱子,如(方法不唯一):给六个箱子分别编号1、2、3、4、5、6号,从每个箱子里取出对应编号数量的小球,共取21个,给这21个小球称重,实际重量必然大于210克,根据多出的重量即可确定次品箱。
【详解】给六个箱子分别编号1、2、3、4、5、6号,从每个箱子里取出对应编号数量的小球,共取出:1+2+3+4+5+6=21(个)
应重:21×10=210(克)
实际重量必定多于210克,多了几克,几号箱中就是次品(如:若5号箱重为次品,那就会多5克,实际重量为215克。)
24.4次
【分析】将61盒分成20盒、20盒、21盒,称量同是20盒的两份,找出轻的一盒在哪份里面。若轻的一盒在20盒这份,将20盒分成7盒、7盒、6盒,称量同是7盒的两份,找出轻的一盒在哪份里面;同理若轻的一盒在21盒这份,将21盒分成7盒、7盒、7盒,任意称量同是7盒的两份,找出轻的一盒在哪份里面。以此类推直到找出次品为止,就能知道至少称量几次能找出轻的一盒。
【详解】第一次称量:将61盒分成20盒、20盒、21盒,找到轻的一盒在哪份里面;
第二次称量:将20盒分成7盒、7盒、6盒,找到轻的一盒在哪份里面;或者将21盒分成7盒、7盒、7盒,任意称量同是7盒的两份,找出轻的一盒在哪份里面;
第三次称量:找到6盒或者7盒里轻的一盒;
第四次称量:找到2盒或者3盒里轻的一盒。
答:至少称量4次能找出轻的一盒。
【点睛】本题考查运用优化策略找次品问题,找次品时,把物体分成3份,每份数量尽量平均时,可以保证所称量的次数最少。
25.至少称4次;
将11枚硬币分成(4、4、3),先称两个4枚,①平衡,次品在3个中,将3个分成(1、1、1),称两个,平衡剩下一个是次品,不平衡,随便拿下一个与剩下的称,即可找出次品;②不平衡,次品在4个中,随便拿出一个放到3个里,确定在哪4个,再称两次确定次品是轻还是重,再称一次即可。
【分析】找次品的最优策略:
(1)把待分物品分成3份;
(2)每份数量尽量平均,如果不能平均分的,也应该使多的一份与少的一份只相差1。
【详解】将11枚硬币分成(4、4、3),先称两个4枚,①平衡,次品在3个中,将3个分成(1、1、1),称两个,平衡剩下一个是次品,不平衡,随便拿下一个与剩下的称,即可找出次品;②不平衡,次品在4个中,随便拿出一个放到3个里,确定在哪4个,再称两次确定次品是轻还是重,再称一次即可。
答:至少称4次。
【点睛】本题考查了找次品,不知道轻重,要确定次品是轻还是重。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
