2024-2025学年北师大版九年级数学下册课件 3.8 圆内接正多边形(26张PPT)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学下册课件 3.8 圆内接正多边形(26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 16:24:42 | ||
图片预览








文档简介
(共26张PPT)
第三章 圆
3.8 圆内接正多边形
1.圆内接正多边形
2.圆内接正多边形的有关概念
3.正多边形的作图(重点、难点)
学习目标
新课导入
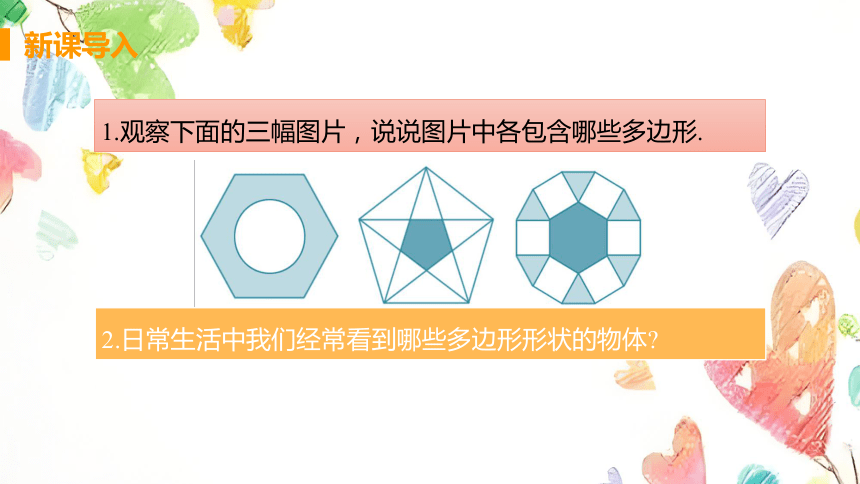
1.观察下面的三幅图片,说说图片中各包含哪些多边形.
2.日常生活中我们经常看到哪些多边形形状的物体
新课讲解
顶点都在同一圆上的正多边形叫做圆内接正多边形.
这个圆叫做该正多边形的外接圆.
新课讲解
正n边形的各角相等,且每个内角为:
每个外角为:
新课讲解
例
如图所示,三角形AOB 是正三角形,以点O 为圆心,
OA 为半径作⊙ O,直径FC ∥ AB,AO,BO 的延长线分别交⊙ O于点D,E,求证:六边形ABCDEF 为圆内接正六边形.
分析:
紧扣正多边形的定义,结合同圆中弧、圆心角的
关系证明.
新课讲解
解:
∵三角形AOB 是正三角形,
∴∠ AOB= ∠ OAB= ∠ OBA=60°,OB=OA.
∴点B 在⊙ O 上.
∵ FC ∥ AB,∴∠ FOA= ∠ OAB=60°,∠ COB=
∠ OBA=60°.
∴∠ AOB= ∠ BOC= ∠ COD= ∠ DOE= ∠ EOF=
∠ FOA=60° .
∴六边形ABCDEF 为圆内接正六边形.
新课讲解
利用尺规作一个已知圆的内接正六边形.
由于正六边形的中心角为60°,因此它的边长就是其外接圆
的半径R.所 以,在半径为R的圆上,依次截取等于R的弦,
就可以六等分圆,进而作出 圆内接正六边形.
新课讲解
例
作一个正三角形,使其半径为0.9 cm.
分析:
用量角器画,先求出其中心角;用尺规画,则先考虑等分圆周.
新课讲解
解:
作法一:
(1)作半径为0.9 cm的⊙O;
(2)用量角器画∠AOB =∠BOC =120°;
(3)连接 AB,BC,CA.则△ABC为所求作的正三角
形,如图所示.
新课讲解
作法二:
(1)作半径为0.9 cm的⊙O;
(2)作⊙O的任一直径AB;
(3)分别以A,B为圆心,以0.9 cm为半径作弧,交
⊙O于点C,F和D,E;(4)连接AD,DE,EA.
则△ADE为所求作的正三角形,如图所示.
课堂小结
正多边形:各边相等、各角也相等的多边形叫做
正多边形.
把一个圆n(n≥3)等分,顺次连接各等分点,就得
到一个正n边形. 我们把这个正n边形叫做圆的内
接正n边形.
当堂小练
1.如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R2-r2=a2
B.a=2Rsin 36°
C.a=2rtan 36°
D.r=Rcos 36°
A
当堂小练
2.在如图所示的圆中,画出你喜欢的三个不同的圆内接正多边形(画图工具不限,但要保留画图痕迹).
解:
如图所示.
(答案不唯一)
拓展与延伸
一个边长为2的正多边形的内角和是其外角和的2倍,则这个正多边形的半径是( )
A.2 B. C.1 D.
A
这个正多边形共有 条对称轴,对称轴都过该多边形的
.
中心
1.如图所示的正多边形中, 是这个正多边形的中心, 是这个正多边形的中心角, 的长是这个正多边形的边心距.
6
该多边形是否为中心对称图形? (填“是”或“否”);若是中心对称图形,则对称中心是 .
点O
是
OP
∠AOB
点O
课后练习
2.(北师9下P105、人教9上P108)填表:
圆内接 正多边形
内角度数
半径 OA=2 OA=2 OA=2
中心角度数
边长
边心距
2
60°
120°
2
90°
90°
1
2
120°
60°
4.【例1】(北师9下P105、人教9上P108)如图,正三角形ABC内接于☉O,AB=2 cm,求☉O的半径.
解:如图,过点O作OD⊥BC于点D,连接BO,
∵正三角形ABC内接于☉O,
∴点O既是三角形的内心也是外心,
∴∠OBD=30°,BD=CD=BC=AB= cm,∴OD=OB,∵OD2+BD2=OB2,+()2=OB2,
解得OB=2,即☉O的半径为2 cm.
5(北师9下P98改编、人教9上P106改编)(2024北京开学)如图,☉O的半径为4.
(1)求作它的内接正六边形ABCDEF;
(2)求正六边形ABCDEF的边长和面积.
解:(1)如图,正六边形ABCDEF就是所求作的正六边形.
答案图
(2)如图,连接OF,OE,且过点O作OH⊥EF,
由正六边形ABCDEF可得△OFE是等边三角形,
∴∠FOH=30°,EF=OF=4,
即正六边形ABCDEF的边长为4.
∴FH=2,根据勾股定理得OH=2 ,
∴S△OFE=4×2 =4 ,
∴S正六边形ABCDEF=6×4 =24
答案图
(2)求正六边形ABCDEF的边长和面积.
6.如图,☉O的半径为2,正方形ABCD,A'B'C'D'分别是☉O的内接正方形和外切正方形,求两个正方形的面积比S内∶S外.
解:如图,连接OA,作OM⊥AD于点M.
∵☉O的半径为2,∴OA=2,
∵在Rt△AOM中,∠OAM=45°,∴OM=OA=,
∴AB=2OM=2 ,A'B'=2OA=4,
∴S内∶S外=AB2∶A'B'2=(AB∶A'B')2
=(2 ∶4)2=
答案图
7.(北师9下P98)如图,正三角形ABC的外接圆☉O的半径为2,求该正三角形的边长.
解:如图,连接OB,过O作OD⊥BC于D,
∵☉O是正三角形ABC的外接圆,
∴OB平分∠ABC,∴∠OBD=30°,
∵∠ODB=90°,∴OD=OB=2=1,
在Rt△OBD中,由勾股定理得BD=,
∵OD⊥BC,∴BC=2BD=2 即该正三角形的边长为2
8.(北师9下P98改编)如图,☉O的半径为4.
(1)求作它的内接正三角形ABC;
(2)求△ABC的面积.
解:(1)如图,△ABC即为所求作.
(2)如图,连接AO,BO,过O作OD⊥AB于D,
∵△ABC是正三角形,
∴∠ABC=60°,∴∠ABO=30°,
∵OB=4,∴OD=2,∴BD=2 ,∴AB=4 ,
∴S△ABO=AB×OD=4 2=4 ,
∴△ABC的面积=3S△ABO=3×4 =12
答案图
★9. 0.50 (创新题)如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依次作到第n个内切圆,它的半径与R的比为___________.
请完成课本本节对应习题
布置作业
谢谢大家观看
第三章 圆
3.8 圆内接正多边形
1.圆内接正多边形
2.圆内接正多边形的有关概念
3.正多边形的作图(重点、难点)
学习目标
新课导入
1.观察下面的三幅图片,说说图片中各包含哪些多边形.
2.日常生活中我们经常看到哪些多边形形状的物体
新课讲解
顶点都在同一圆上的正多边形叫做圆内接正多边形.
这个圆叫做该正多边形的外接圆.
新课讲解
正n边形的各角相等,且每个内角为:
每个外角为:
新课讲解
例
如图所示,三角形AOB 是正三角形,以点O 为圆心,
OA 为半径作⊙ O,直径FC ∥ AB,AO,BO 的延长线分别交⊙ O于点D,E,求证:六边形ABCDEF 为圆内接正六边形.
分析:
紧扣正多边形的定义,结合同圆中弧、圆心角的
关系证明.
新课讲解
解:
∵三角形AOB 是正三角形,
∴∠ AOB= ∠ OAB= ∠ OBA=60°,OB=OA.
∴点B 在⊙ O 上.
∵ FC ∥ AB,∴∠ FOA= ∠ OAB=60°,∠ COB=
∠ OBA=60°.
∴∠ AOB= ∠ BOC= ∠ COD= ∠ DOE= ∠ EOF=
∠ FOA=60° .
∴六边形ABCDEF 为圆内接正六边形.
新课讲解
利用尺规作一个已知圆的内接正六边形.
由于正六边形的中心角为60°,因此它的边长就是其外接圆
的半径R.所 以,在半径为R的圆上,依次截取等于R的弦,
就可以六等分圆,进而作出 圆内接正六边形.
新课讲解
例
作一个正三角形,使其半径为0.9 cm.
分析:
用量角器画,先求出其中心角;用尺规画,则先考虑等分圆周.
新课讲解
解:
作法一:
(1)作半径为0.9 cm的⊙O;
(2)用量角器画∠AOB =∠BOC =120°;
(3)连接 AB,BC,CA.则△ABC为所求作的正三角
形,如图所示.
新课讲解
作法二:
(1)作半径为0.9 cm的⊙O;
(2)作⊙O的任一直径AB;
(3)分别以A,B为圆心,以0.9 cm为半径作弧,交
⊙O于点C,F和D,E;(4)连接AD,DE,EA.
则△ADE为所求作的正三角形,如图所示.
课堂小结
正多边形:各边相等、各角也相等的多边形叫做
正多边形.
把一个圆n(n≥3)等分,顺次连接各等分点,就得
到一个正n边形. 我们把这个正n边形叫做圆的内
接正n边形.
当堂小练
1.如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R2-r2=a2
B.a=2Rsin 36°
C.a=2rtan 36°
D.r=Rcos 36°
A
当堂小练
2.在如图所示的圆中,画出你喜欢的三个不同的圆内接正多边形(画图工具不限,但要保留画图痕迹).
解:
如图所示.
(答案不唯一)
拓展与延伸
一个边长为2的正多边形的内角和是其外角和的2倍,则这个正多边形的半径是( )
A.2 B. C.1 D.
A
这个正多边形共有 条对称轴,对称轴都过该多边形的
.
中心
1.如图所示的正多边形中, 是这个正多边形的中心, 是这个正多边形的中心角, 的长是这个正多边形的边心距.
6
该多边形是否为中心对称图形? (填“是”或“否”);若是中心对称图形,则对称中心是 .
点O
是
OP
∠AOB
点O
课后练习
2.(北师9下P105、人教9上P108)填表:
圆内接 正多边形
内角度数
半径 OA=2 OA=2 OA=2
中心角度数
边长
边心距
2
60°
120°
2
90°
90°
1
2
120°
60°
4.【例1】(北师9下P105、人教9上P108)如图,正三角形ABC内接于☉O,AB=2 cm,求☉O的半径.
解:如图,过点O作OD⊥BC于点D,连接BO,
∵正三角形ABC内接于☉O,
∴点O既是三角形的内心也是外心,
∴∠OBD=30°,BD=CD=BC=AB= cm,∴OD=OB,∵OD2+BD2=OB2,+()2=OB2,
解得OB=2,即☉O的半径为2 cm.
5(北师9下P98改编、人教9上P106改编)(2024北京开学)如图,☉O的半径为4.
(1)求作它的内接正六边形ABCDEF;
(2)求正六边形ABCDEF的边长和面积.
解:(1)如图,正六边形ABCDEF就是所求作的正六边形.
答案图
(2)如图,连接OF,OE,且过点O作OH⊥EF,
由正六边形ABCDEF可得△OFE是等边三角形,
∴∠FOH=30°,EF=OF=4,
即正六边形ABCDEF的边长为4.
∴FH=2,根据勾股定理得OH=2 ,
∴S△OFE=4×2 =4 ,
∴S正六边形ABCDEF=6×4 =24
答案图
(2)求正六边形ABCDEF的边长和面积.
6.如图,☉O的半径为2,正方形ABCD,A'B'C'D'分别是☉O的内接正方形和外切正方形,求两个正方形的面积比S内∶S外.
解:如图,连接OA,作OM⊥AD于点M.
∵☉O的半径为2,∴OA=2,
∵在Rt△AOM中,∠OAM=45°,∴OM=OA=,
∴AB=2OM=2 ,A'B'=2OA=4,
∴S内∶S外=AB2∶A'B'2=(AB∶A'B')2
=(2 ∶4)2=
答案图
7.(北师9下P98)如图,正三角形ABC的外接圆☉O的半径为2,求该正三角形的边长.
解:如图,连接OB,过O作OD⊥BC于D,
∵☉O是正三角形ABC的外接圆,
∴OB平分∠ABC,∴∠OBD=30°,
∵∠ODB=90°,∴OD=OB=2=1,
在Rt△OBD中,由勾股定理得BD=,
∵OD⊥BC,∴BC=2BD=2 即该正三角形的边长为2
8.(北师9下P98改编)如图,☉O的半径为4.
(1)求作它的内接正三角形ABC;
(2)求△ABC的面积.
解:(1)如图,△ABC即为所求作.
(2)如图,连接AO,BO,过O作OD⊥AB于D,
∵△ABC是正三角形,
∴∠ABC=60°,∴∠ABO=30°,
∵OB=4,∴OD=2,∴BD=2 ,∴AB=4 ,
∴S△ABO=AB×OD=4 2=4 ,
∴△ABC的面积=3S△ABO=3×4 =12
答案图
★9. 0.50 (创新题)如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依次作到第n个内切圆,它的半径与R的比为___________.
请完成课本本节对应习题
布置作业
谢谢大家观看
