华师大七年级下册第7章7.2二元一次方程组的解法
文档属性
| 名称 | 华师大七年级下册第7章7.2二元一次方程组的解法 |
|
|
| 格式 | doc | ||
| 文件大小 | 331.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-21 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版七年级下册第7章第2节7.2二元一次方程组的解法课时练习
一、单选题(共15小题)
1.某校初三(2)班40名同学为"希望工程"捐款,共捐款100元.捐款情况如下表:
捐款元 1 2 3 4
人数 6 7
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.
若设捐款2 元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组 ( )
A.x+y=27,2x+3y=66 B.x+y=27,2x+3y=100
C.x+y=27,3x+2y=66 D.x+y=27,3x+2y=100
答案:A
解答:题目当中包含两个等量关系,捐款2元和捐款3元的人数之和为,捐款2元和捐款3元捐款总额为元,根据这两等量关系列出二元一次方程组,故选A.
分析:应用二元一次方程组解题时,注意找出题目当中的等量关系(一般有两个等量关系式)分别列出两个方程并正确求解.
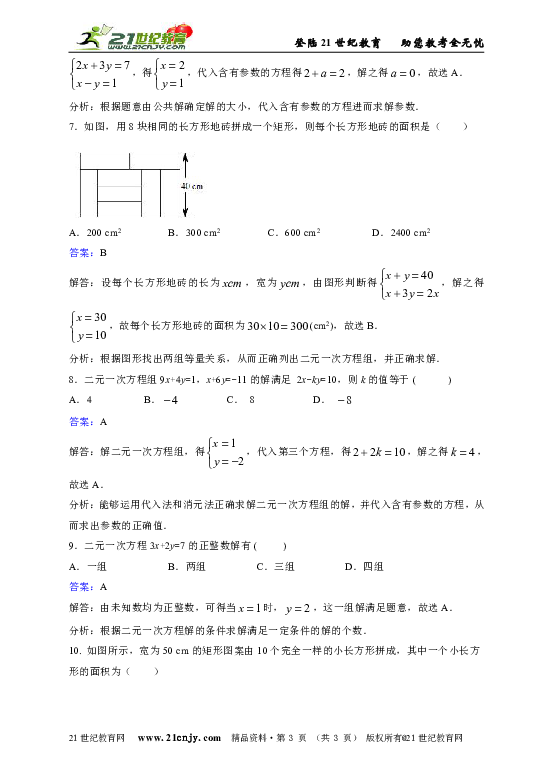
2. 陈老师打算购买气球装扮学校"六一"儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4 个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( ).
A.19 B.18 C.16 D.15
答案:C
解答:设爱心气球每个元,笑脸气球每个元,由第一束和第二束的价格,可得二元一次方程组,解之得,则第三束气球的价格为(元),故选C.
分析:应用二元一次方程组解答实际问题时,题目当中往往包含了两个等量关系式,学生应能够正确设未知数,并找出等量关系正确列出方程组,进而正确求解即可.
3.如果关于 x,y 的方程组 的解是二元一次方程 3x+2y=14的一个解,那么m的值为 ( )
A. B. C. D.
答案:C
解答:解二元一次方程组得,,代入二元一次方程,得,故,故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )分析:解答含有参数的二元一次方程组时,可把参数当作已知量,用参数代表未知数,进而代入第三个方程从而求解出参数的值.
4.将一张面值100元的人民币,兑换成10元或20元的零钱,兑换方案有 ( )
A.6种 B.7种 C.8种 D.9种
答案:A
解答:由题意,设兑换成10元的张,兑换成20元的元,则由题意,得(其中、都是非负整数),所以当等于0、2、4、6、8、10时,相应取、、、、、,故共有6种方案,故选A.
分析:根据题意正确列出二元一次方程,并注意隐含条件未知数是非负整数,从而确定方案个数.
5.已知 3x+y=4,x+3y=8. 那么 x+y 的值为 ( )
A.3 B.6 C.9 D.12
答案:A
解答:解方程组得,所以,故选A.
分析:正确应用代入法或消元法解二元一次方程组是本章的重点.
6.已知方程组x+ay=2,2x+3y=7的解也是二元一次方程x-y=1的一个解,则a的值是 ( )
A.0 B.1 C.2 D.3
答案:A
解答:由题意,三个方程有公共解,解没有参数的两个二元一次方程组成的二元一次方程组,得,代入含有参数的方程得,解之得,故选A.
分析:根据题意由公共解确定解的大小,代入含有参数的方程进而求解参数.
7.如图,用8块相同的长方形地砖拼成一个矩形,则每个长方形地砖的面积是( )
A.200 cm2 B.300 cm2 C.600 cm2 D.2400 cm2
答案:B
解答:设每个长方形地砖的长为,宽为,由图形判断得,解之得,故每个长方形地砖的面积为(cm2),故选B.
分析:根据图形找出两组等量关系,从而正确列出二元一次方程组,并正确求解.
8.二元一次方程组9x+4y=1,x+6y=-11的解满足 2x-ky=10,则k的值等于 ( )
A.4 B. C. 8 D.
答案:A
解答:解二元一次方程组,得,代入第三个方程,得,解之得,故选A.
分析:能够运用代入法和消元法正确求解二元一次方程组的解,并代入含有参数的方程,从而求出参数的正确值.
9.二元一次方程3x+2y=7的正整数解有 ( )
A.一组 B.两组 C.三组 D.四组
答案:A
解答:由未知数均为正整数,可得当时,,这一组解满足题意,故选A.
分析:根据二元一次方程解的条件求解满足一定条件的解的个数.
10. 如图所示,宽为50 cm的矩形图案由10个完全一样的小长方形拼成,其中一个小长方形的面积为( )
A.400 cm2 B.500 cm2 C.600 cm2 D.4000 cm2
答案:A
解答:设小长方形的长为,宽为,由图案特征得,解之得,故小长方形的面积为(cm2),故选A.
分析:根据题意找出两组等量关系,并分别列出关于未知数的二元一次方程,组成二元一次方程组,并正确求解.
11.甲、乙两人年收入之比为4:3,支出之比为8:5,一年间两人各存入5000元(设两人剩余的钱都存入银行),则甲、乙两人年收入分别为 ( )
A.16000 元、 12000 元 B.12000 元、 15000 元
C.15000 元、 11250 元 D.11250 元、 15000 元
答案:C
解答:解设甲的年收入为元,则乙的年收入为元,设甲的年支出为元,则乙的年支出为元,由题意,得方程组,解之得,则甲年收入为(元),乙的年收入为(元),故选C.
分析:根据题意,合理设出未知数,并找出两组等量关系正确列出二元一次方程组,并正确求解.
12.已知 2x+3y=z,3x+4y=2z+6. 且x+y=3,则z的值为 ( )
A.9 B. C.12 D.无解
答案:B
解答:将方程中的代入第二个方程,得,与第三个方程联立,得方程组,解之得,所以,故选B.
分析:利用消元法先消去一个未知数,这样的方法通常用于解多元一次方程组当中,学生应能了解和掌握.
13.已知x=-2,y=4. 和x=4,y=1.都是方程y=ax+b的解,则a和b的值是 ( )
A. a=12,b=5 B.a=,b=3 C.a=12,b=3 D.a=-12,b=-1
答案:B
解答:将方程的解代入方程当中,得方程组,解之得,故选B.
分析:根据方程的定义,方程的解代入方程反解参数的值是解这类题型的基本方法.
14.现有球迷150人欲同时租用A 、 B 、 C 三种型号客车去观看世界杯足球赛,其中 A 、 B 、 C 三种型号客车载客量分别为50 人、 30 人、 10人,要求每辆车必须满载,其中A型客车最多租两辆,则球迷们一次性到达赛场的租车方案有 ( )
A. 3种 B.4种 C.5种 D.6种
答案:B
解答:设租A、B、C三种型号的车分别为、、由题意,得方程,当时,得,有,,三组解,当时,得,有一组解,所以共有四组解,故选B.
分析:正确列出多元一次方程,并根据题目约束条件,求解解的个数.
15.周长为68的矩形ABCD被分成7个全等的矩形,则如图所示中,矩形ABCD面积为( )
A.98 B.196 C.280 D.284
答案:C
解答:设小长方形的长为,宽为,由题意,得,解之得,故矩形ABCD的长为,宽为,其面积为,故选C.
分析:根据题意正确设立未知数,并列出相关方程组,正确求解即可.
二、填空题(共5小题)
16.若方程组 x+by=0,x+y=-1的解是x=1,y=▲. 其中y的值被墨渍盖住了,则b的值是________.
答案:
解答:将代入,得,代入方程得,解之得.
分析:学生能通过代入方程组的解的定义,将方程组的解代入方程,反求参数的值,从而实现新方程的建立.
17.现有载重 3 吨的卡车x辆,载重5吨的卡车比载重3吨的卡车多4辆,它们一共能运货y吨,那么依题意,可列出方程为 .
答案:y=8x+20
解答:根据题意,载重3吨的卡车辆,则载重5吨的卡车为辆,则由一共运吨,得等量关系式,整理得y=8x+20.
分析:根据题意,正确找出题目当中包含的等量关系,从而列出方程.
18. 学校举行“大家唱大家跳”文艺汇演,设置了歌唱与舞蹈两类节目,全校师生一共表演了30个节目,其中歌唱类节目比舞蹈类节目的3倍少2个,则全校师生表演的歌唱类节目有 个.
答案:22
解答:由题意,设舞蹈类节目为个,则歌唱类节目为个,由题意,得,解之得,歌唱类节目为(个).
分析:学生可通过复习一元一次方程的应用进一步温故知新,了解二元一次方程建立的一般过程.
19.若方程组 ax+a-y=6,4x+3y=14 的解x 、y的值相等,则 a 的值为 .
答案:
解答:由题意,得到关于、的方程组为,解之得.
分析:充分运用已知条件和相等,实现消元的过程,从而进一步求解参数的值.
20.水仙花是漳州市花,如图,在长为14 m,宽为10m 的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为 m.
答案:16
解答:设每个小长方形的长为,宽为,由题意,得,解之得,所以小长方形的周长为.
分析:根据组成大长方形的小长方形的长宽个数分别找出等量关系,并列出方程组,正确求解,得出正解.
三、解答题(共5小题)
21.解方程组
答案:
解答:②×3-① 得 11y=22,即y=2,
把 y=2 代入 ② 得x=1,
则方程组的解为
x=1,y=2.
分析:运用消元法正确求解二元一次方程组的解是学生应掌握的基本知识.
22.小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.妈妈:“今天买这两样菜共花了45元,上月买同重量的这两样菜只要36元”;爸爸:“报纸上说了萝卜的单价上涨了50%,排骨单价上涨了20% ”;小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤)
答案:这天萝卜的单价是 3 元/斤,排骨的单价是 18 元/斤
解答:设上月萝卜的单价是 x 元/斤,排骨的单价 y 元/斤,根据题意得
,解得x=2,y=15.
所以 (1+50%)x=(1+50%)×2=3,(1+20%)y=(1+20%)×15=18.
分析:正确分析题目陈述,把握等量关系,合理设置未知数,列出二元一次方程组,并正确求解.
23.某同学在A,B两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元.
(1)求该同学看中的随身听和书包单价各是多少元?
答案:书包每个92元,随身听每个为360元
解答: 设书包的单价为x元,随身听的单价为y元.根据题意,得
解这个方程组,得x=92,y=360.
(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱 ?
答案:在超市A购买更省钱
解答:在超市A购买随身听与书包各一件需花费现金:
452×80%=361.6.在超市 B 可先花费现金360元购买随身听,再利用得到的90元返券,加上2元现金购买书包,总计共需花费现金:360+2=362元.
虽然在两个商场的消费都小于 400 元,但因为 362>361.6,所以在超市 A 购买更省钱.
分析:合理分析题目陈述,把握住题目当中包含的等量关系,列出方程组,并进行数学分析,是解题的关键.
24. 某公司欲租赁甲、乙两种设备,用来生产A产品80件、 B产品100件.已知甲种设备每天租赁费为400元,每天满负荷可生产A产品12件和B产品10件;乙种设备每天租赁费为300元,每天满负荷可生产A产品7件和B产品10件.
(1)若在租赁期间甲、乙两种设备每天均满负荷生产,则需租赁甲、乙两种设备各多少天恰好完成生产任务?
答案:需租赁甲种设备 2 天、乙种设备 8 天
解答:设需租赁甲、乙两种设备分别为x,y天,则依题意得,
解得x=2,y=8.
(2)若甲种设备最多只能租赁5天,乙种设备最多只能租赁7天,该公司为确保完成生产任务,决定租赁这两种设备合计10天(两种设备的租赁天数均为整数),问该公司共有哪几种租赁方案可供选择?所需租赁费最少是多少?
答案:共有 3 种租赁方案:①甲 3 天、乙 7 天;②甲 4 天、乙 6 天;③甲 5 天、乙 5 天.最少租赁费用 3300 元.
解答:设租赁甲种设备a天、乙种设备10﹣a天,总费用为w元,根据题意得
a≤5,10-a≤7,12a+710-a≥80,10a+1010-a≥100,
∴3≤a≤5,
∵a为整数,
∴a=3,4,5,
方法一:∴ 共有三种方案.
方案1:甲3天、乙7天,总费用400×3+300×7=3300;
方案2:甲4天、乙6天,总费用400×4+300×6=3400;
方案3:甲5天、乙5天,总费用400×5+300×5=3500;
∵3300<3400<3500,
∴ 方案1最省,最省费用为3300元;
方法二:则w=400a+300(10-a)=100a+3000,
∵100>0,
∴w随a的增大而增大,
∴ 当a=3时,w最小=100×3+3000=3300.
分析:题目当中包含了两组等量关系,需要分析提取出来,并正确设置未知数,列出方程组,并进行数值分析是运用数学知识解决实际问题的关键,也体现了数学的逻辑性和实用性.
25.阅读材料:善于思考的小军在解方程组 2x+5y=3, ①4x+11y=5 ② 时,采用了一种“整体代换”的解法:
解:将方程②变形:4x+10y+y=5,即 22x+5y+y=5,③
把方程①代入③得 2×3+y=5,
∴y=-1.
把 y=-1 代入 ① 得,x=4,
∴ 方程组的解为 x=4,y=-1.
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组3x-2y=5,①9x-4y=19.②
答案:
解答:将方程②变形得3(3x-2y)+2y=19,③
把方程①代入③得3×5+2y=19,
∴y=2.
把y=2代入方程①得x=3.
∴ 方程组的解为x=3,y=2. (2)已知x,y满足方程组 3x2-2xy+12y2=47,①2x2+xy+8y2=36,②
求 x2+4y2 的值;
答案:17
解答:由方程 ② 得2(x2+4y2)+xy=36,
∴xy=36-2(x2+4y2),③
由方程①得3(x2+4y2)-2xy=47,④
③代入④得,3(x2+4y2)-2[36-2(x2+4y2)]=47,
∴x2+4y2=17.
分析:运用特殊技巧解答特殊方程,是学生灵活运用所学知识有所创新的一个过程,实现继往开来的突破.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 10 页 (共 10 页) 版权所有@21世纪教育网
华师大版七年级下册第7章第2节7.2二元一次方程组的解法课时练习
一、单选题(共15小题)
1.某校初三(2)班40名同学为"希望工程"捐款,共捐款100元.捐款情况如下表:
捐款元 1 2 3 4
人数 6 7
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.
若设捐款2 元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组 ( )
A.x+y=27,2x+3y=66 B.x+y=27,2x+3y=100
C.x+y=27,3x+2y=66 D.x+y=27,3x+2y=100
答案:A
解答:题目当中包含两个等量关系,捐款2元和捐款3元的人数之和为,捐款2元和捐款3元捐款总额为元,根据这两等量关系列出二元一次方程组,故选A.
分析:应用二元一次方程组解题时,注意找出题目当中的等量关系(一般有两个等量关系式)分别列出两个方程并正确求解.
2. 陈老师打算购买气球装扮学校"六一"儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4 个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( ).
A.19 B.18 C.16 D.15
答案:C
解答:设爱心气球每个元,笑脸气球每个元,由第一束和第二束的价格,可得二元一次方程组,解之得,则第三束气球的价格为(元),故选C.
分析:应用二元一次方程组解答实际问题时,题目当中往往包含了两个等量关系式,学生应能够正确设未知数,并找出等量关系正确列出方程组,进而正确求解即可.
3.如果关于 x,y 的方程组 的解是二元一次方程 3x+2y=14的一个解,那么m的值为 ( )
A. B. C. D.
答案:C
解答:解二元一次方程组得,,代入二元一次方程,得,故,故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )分析:解答含有参数的二元一次方程组时,可把参数当作已知量,用参数代表未知数,进而代入第三个方程从而求解出参数的值.
4.将一张面值100元的人民币,兑换成10元或20元的零钱,兑换方案有 ( )
A.6种 B.7种 C.8种 D.9种
答案:A
解答:由题意,设兑换成10元的张,兑换成20元的元,则由题意,得(其中、都是非负整数),所以当等于0、2、4、6、8、10时,相应取、、、、、,故共有6种方案,故选A.
分析:根据题意正确列出二元一次方程,并注意隐含条件未知数是非负整数,从而确定方案个数.
5.已知 3x+y=4,x+3y=8. 那么 x+y 的值为 ( )
A.3 B.6 C.9 D.12
答案:A
解答:解方程组得,所以,故选A.
分析:正确应用代入法或消元法解二元一次方程组是本章的重点.
6.已知方程组x+ay=2,2x+3y=7的解也是二元一次方程x-y=1的一个解,则a的值是 ( )
A.0 B.1 C.2 D.3
答案:A
解答:由题意,三个方程有公共解,解没有参数的两个二元一次方程组成的二元一次方程组,得,代入含有参数的方程得,解之得,故选A.
分析:根据题意由公共解确定解的大小,代入含有参数的方程进而求解参数.
7.如图,用8块相同的长方形地砖拼成一个矩形,则每个长方形地砖的面积是( )
A.200 cm2 B.300 cm2 C.600 cm2 D.2400 cm2
答案:B
解答:设每个长方形地砖的长为,宽为,由图形判断得,解之得,故每个长方形地砖的面积为(cm2),故选B.
分析:根据图形找出两组等量关系,从而正确列出二元一次方程组,并正确求解.
8.二元一次方程组9x+4y=1,x+6y=-11的解满足 2x-ky=10,则k的值等于 ( )
A.4 B. C. 8 D.
答案:A
解答:解二元一次方程组,得,代入第三个方程,得,解之得,故选A.
分析:能够运用代入法和消元法正确求解二元一次方程组的解,并代入含有参数的方程,从而求出参数的正确值.
9.二元一次方程3x+2y=7的正整数解有 ( )
A.一组 B.两组 C.三组 D.四组
答案:A
解答:由未知数均为正整数,可得当时,,这一组解满足题意,故选A.
分析:根据二元一次方程解的条件求解满足一定条件的解的个数.
10. 如图所示,宽为50 cm的矩形图案由10个完全一样的小长方形拼成,其中一个小长方形的面积为( )
A.400 cm2 B.500 cm2 C.600 cm2 D.4000 cm2
答案:A
解答:设小长方形的长为,宽为,由图案特征得,解之得,故小长方形的面积为(cm2),故选A.
分析:根据题意找出两组等量关系,并分别列出关于未知数的二元一次方程,组成二元一次方程组,并正确求解.
11.甲、乙两人年收入之比为4:3,支出之比为8:5,一年间两人各存入5000元(设两人剩余的钱都存入银行),则甲、乙两人年收入分别为 ( )
A.16000 元、 12000 元 B.12000 元、 15000 元
C.15000 元、 11250 元 D.11250 元、 15000 元
答案:C
解答:解设甲的年收入为元,则乙的年收入为元,设甲的年支出为元,则乙的年支出为元,由题意,得方程组,解之得,则甲年收入为(元),乙的年收入为(元),故选C.
分析:根据题意,合理设出未知数,并找出两组等量关系正确列出二元一次方程组,并正确求解.
12.已知 2x+3y=z,3x+4y=2z+6. 且x+y=3,则z的值为 ( )
A.9 B. C.12 D.无解
答案:B
解答:将方程中的代入第二个方程,得,与第三个方程联立,得方程组,解之得,所以,故选B.
分析:利用消元法先消去一个未知数,这样的方法通常用于解多元一次方程组当中,学生应能了解和掌握.
13.已知x=-2,y=4. 和x=4,y=1.都是方程y=ax+b的解,则a和b的值是 ( )
A. a=12,b=5 B.a=,b=3 C.a=12,b=3 D.a=-12,b=-1
答案:B
解答:将方程的解代入方程当中,得方程组,解之得,故选B.
分析:根据方程的定义,方程的解代入方程反解参数的值是解这类题型的基本方法.
14.现有球迷150人欲同时租用A 、 B 、 C 三种型号客车去观看世界杯足球赛,其中 A 、 B 、 C 三种型号客车载客量分别为50 人、 30 人、 10人,要求每辆车必须满载,其中A型客车最多租两辆,则球迷们一次性到达赛场的租车方案有 ( )
A. 3种 B.4种 C.5种 D.6种
答案:B
解答:设租A、B、C三种型号的车分别为、、由题意,得方程,当时,得,有,,三组解,当时,得,有一组解,所以共有四组解,故选B.
分析:正确列出多元一次方程,并根据题目约束条件,求解解的个数.
15.周长为68的矩形ABCD被分成7个全等的矩形,则如图所示中,矩形ABCD面积为( )
A.98 B.196 C.280 D.284
答案:C
解答:设小长方形的长为,宽为,由题意,得,解之得,故矩形ABCD的长为,宽为,其面积为,故选C.
分析:根据题意正确设立未知数,并列出相关方程组,正确求解即可.
二、填空题(共5小题)
16.若方程组 x+by=0,x+y=-1的解是x=1,y=▲. 其中y的值被墨渍盖住了,则b的值是________.
答案:
解答:将代入,得,代入方程得,解之得.
分析:学生能通过代入方程组的解的定义,将方程组的解代入方程,反求参数的值,从而实现新方程的建立.
17.现有载重 3 吨的卡车x辆,载重5吨的卡车比载重3吨的卡车多4辆,它们一共能运货y吨,那么依题意,可列出方程为 .
答案:y=8x+20
解答:根据题意,载重3吨的卡车辆,则载重5吨的卡车为辆,则由一共运吨,得等量关系式,整理得y=8x+20.
分析:根据题意,正确找出题目当中包含的等量关系,从而列出方程.
18. 学校举行“大家唱大家跳”文艺汇演,设置了歌唱与舞蹈两类节目,全校师生一共表演了30个节目,其中歌唱类节目比舞蹈类节目的3倍少2个,则全校师生表演的歌唱类节目有 个.
答案:22
解答:由题意,设舞蹈类节目为个,则歌唱类节目为个,由题意,得,解之得,歌唱类节目为(个).
分析:学生可通过复习一元一次方程的应用进一步温故知新,了解二元一次方程建立的一般过程.
19.若方程组 ax+a-y=6,4x+3y=14 的解x 、y的值相等,则 a 的值为 .
答案:
解答:由题意,得到关于、的方程组为,解之得.
分析:充分运用已知条件和相等,实现消元的过程,从而进一步求解参数的值.
20.水仙花是漳州市花,如图,在长为14 m,宽为10m 的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为 m.
答案:16
解答:设每个小长方形的长为,宽为,由题意,得,解之得,所以小长方形的周长为.
分析:根据组成大长方形的小长方形的长宽个数分别找出等量关系,并列出方程组,正确求解,得出正解.
三、解答题(共5小题)
21.解方程组
答案:
解答:②×3-① 得 11y=22,即y=2,
把 y=2 代入 ② 得x=1,
则方程组的解为
x=1,y=2.
分析:运用消元法正确求解二元一次方程组的解是学生应掌握的基本知识.
22.小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.妈妈:“今天买这两样菜共花了45元,上月买同重量的这两样菜只要36元”;爸爸:“报纸上说了萝卜的单价上涨了50%,排骨单价上涨了20% ”;小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤)
答案:这天萝卜的单价是 3 元/斤,排骨的单价是 18 元/斤
解答:设上月萝卜的单价是 x 元/斤,排骨的单价 y 元/斤,根据题意得
,解得x=2,y=15.
所以 (1+50%)x=(1+50%)×2=3,(1+20%)y=(1+20%)×15=18.
分析:正确分析题目陈述,把握等量关系,合理设置未知数,列出二元一次方程组,并正确求解.
23.某同学在A,B两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元.
(1)求该同学看中的随身听和书包单价各是多少元?
答案:书包每个92元,随身听每个为360元
解答: 设书包的单价为x元,随身听的单价为y元.根据题意,得
解这个方程组,得x=92,y=360.
(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱 ?
答案:在超市A购买更省钱
解答:在超市A购买随身听与书包各一件需花费现金:
452×80%=361.6.在超市 B 可先花费现金360元购买随身听,再利用得到的90元返券,加上2元现金购买书包,总计共需花费现金:360+2=362元.
虽然在两个商场的消费都小于 400 元,但因为 362>361.6,所以在超市 A 购买更省钱.
分析:合理分析题目陈述,把握住题目当中包含的等量关系,列出方程组,并进行数学分析,是解题的关键.
24. 某公司欲租赁甲、乙两种设备,用来生产A产品80件、 B产品100件.已知甲种设备每天租赁费为400元,每天满负荷可生产A产品12件和B产品10件;乙种设备每天租赁费为300元,每天满负荷可生产A产品7件和B产品10件.
(1)若在租赁期间甲、乙两种设备每天均满负荷生产,则需租赁甲、乙两种设备各多少天恰好完成生产任务?
答案:需租赁甲种设备 2 天、乙种设备 8 天
解答:设需租赁甲、乙两种设备分别为x,y天,则依题意得,
解得x=2,y=8.
(2)若甲种设备最多只能租赁5天,乙种设备最多只能租赁7天,该公司为确保完成生产任务,决定租赁这两种设备合计10天(两种设备的租赁天数均为整数),问该公司共有哪几种租赁方案可供选择?所需租赁费最少是多少?
答案:共有 3 种租赁方案:①甲 3 天、乙 7 天;②甲 4 天、乙 6 天;③甲 5 天、乙 5 天.最少租赁费用 3300 元.
解答:设租赁甲种设备a天、乙种设备10﹣a天,总费用为w元,根据题意得
a≤5,10-a≤7,12a+710-a≥80,10a+1010-a≥100,
∴3≤a≤5,
∵a为整数,
∴a=3,4,5,
方法一:∴ 共有三种方案.
方案1:甲3天、乙7天,总费用400×3+300×7=3300;
方案2:甲4天、乙6天,总费用400×4+300×6=3400;
方案3:甲5天、乙5天,总费用400×5+300×5=3500;
∵3300<3400<3500,
∴ 方案1最省,最省费用为3300元;
方法二:则w=400a+300(10-a)=100a+3000,
∵100>0,
∴w随a的增大而增大,
∴ 当a=3时,w最小=100×3+3000=3300.
分析:题目当中包含了两组等量关系,需要分析提取出来,并正确设置未知数,列出方程组,并进行数值分析是运用数学知识解决实际问题的关键,也体现了数学的逻辑性和实用性.
25.阅读材料:善于思考的小军在解方程组 2x+5y=3, ①4x+11y=5 ② 时,采用了一种“整体代换”的解法:
解:将方程②变形:4x+10y+y=5,即 22x+5y+y=5,③
把方程①代入③得 2×3+y=5,
∴y=-1.
把 y=-1 代入 ① 得,x=4,
∴ 方程组的解为 x=4,y=-1.
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组3x-2y=5,①9x-4y=19.②
答案:
解答:将方程②变形得3(3x-2y)+2y=19,③
把方程①代入③得3×5+2y=19,
∴y=2.
把y=2代入方程①得x=3.
∴ 方程组的解为x=3,y=2. (2)已知x,y满足方程组 3x2-2xy+12y2=47,①2x2+xy+8y2=36,②
求 x2+4y2 的值;
答案:17
解答:由方程 ② 得2(x2+4y2)+xy=36,
∴xy=36-2(x2+4y2),③
由方程①得3(x2+4y2)-2xy=47,④
③代入④得,3(x2+4y2)-2[36-2(x2+4y2)]=47,
∴x2+4y2=17.
分析:运用特殊技巧解答特殊方程,是学生灵活运用所学知识有所创新的一个过程,实现继往开来的突破.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 10 页 (共 10 页) 版权所有@21世纪教育网
